Wolumetryczna gęstość energii pola elektrostatycznego kuli

(Przykłady rozwiązania problemu)

Energia interakcji ładunku

Przykład 1.

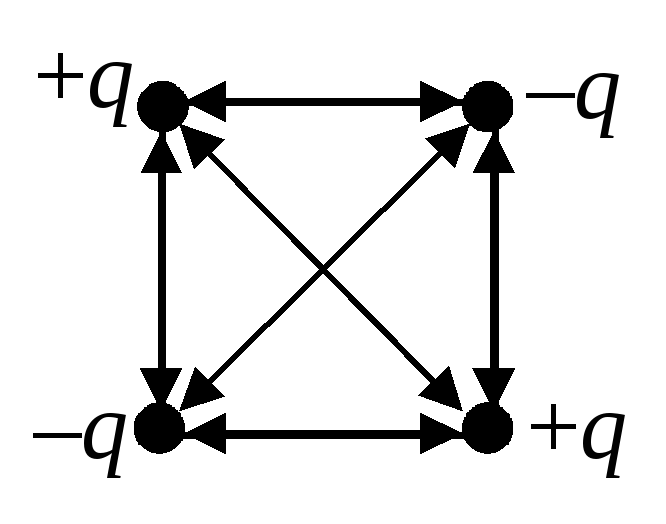
Wyznacz energię elektryczną oddziaływania ładunków punktowych znajdujących się na wierzchołkach kwadratu o boku A(patrz ryc. 2).

Rozwiązanie.

Na ryc. 3 wszystkie sparowane oddziaływania ładunków są konwencjonalnie przedstawione za pomocą strzałek o podwójnym kierunku. Biorąc pod uwagę energie wszystkich tych oddziaływań, otrzymujemy:

Przykład 2.

Wyznacz energię elektryczną oddziaływania naładowanego pierścienia z dipolem umieszczonym na jego osi, jak pokazano na rys. 4. Znane odległości A, l, opłaty Q, Q i promień pierścienia R.

Rozwiązanie.

Rozwiązując zadanie należy uwzględnić wszystkie energie oddziaływań par ładunków jednego ciała (pierścienia) z ładunkami drugiego ciała (dipol). Energia interakcji opłata punktowa Q z opłatą Q rozłożony na pierścień jest określany przez sumę

Gdzie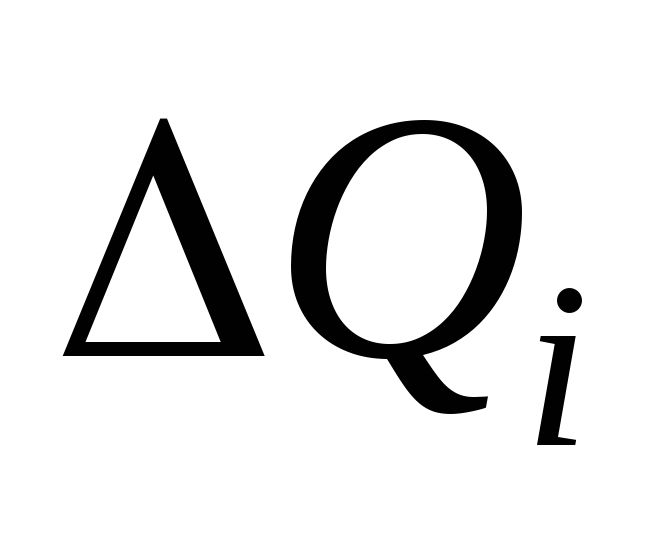

- ładunek nieskończenie małego fragmentu pierścienia, - odległość tego fragmentu od ładunku Q. Ponieważ wszystko takie same i równe

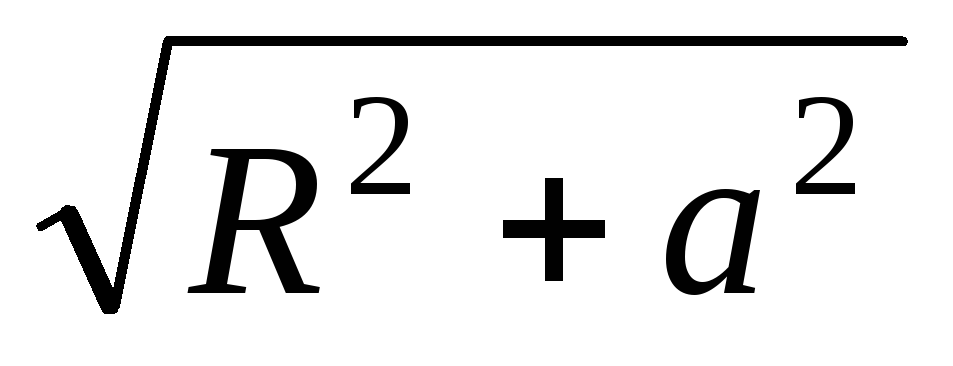, To

Podobnie znajdujemy energię interakcji ładunku punktowego – Q z naładowanym pierścieniem:

Zreasumowanie W 1 i W 2, dla energii oddziaływania pierścienia z dipolem otrzymujemy:

Energia elektryczna naładowanych przewodników

Przykład 3.

Zdefiniuj pracę siły elektryczne gdy promień równomiernie naładowanej kuli zmniejsza się 2-krotnie. Ładunek kuli Q, jego początkowy promień R.

Rozwiązanie.

Energię elektryczną pojedynczego przewodnika określa się ze wzoru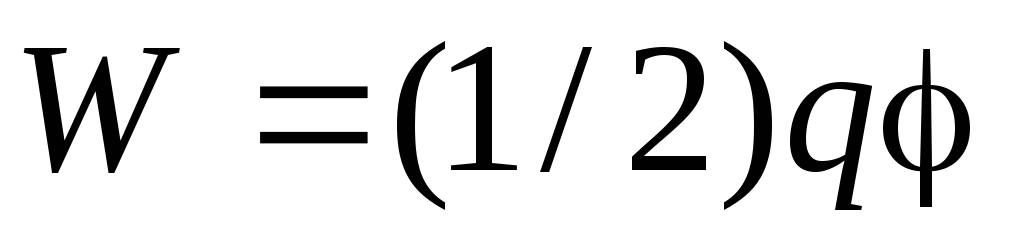

, Gdzie Q– ładunek przewodnika,  – jego potencjał. Biorąc pod uwagę potencjał równomiernie naładowanej kuli o promieniu R równa się

, znajdźmy jego energię elektryczną:

Po zmniejszeniu promienia kuli o połowę jej energia staje się równa

Siły elektryczne działają

Przykład 4.

Dwie metalowe kulki, których promień wynosi R i 2 R, a odpowiadające im ładunki wynoszą 2 Q I - Q, znajdujące się w próżni w dużej odległości od siebie. Ile razy to się zmniejszy energia elektryczna system, jeśli kulki są połączone cienkim drutem?

Rozwiązanie.

Po połączeniu kulek cienkim drutem ich potencjały stają się takie same

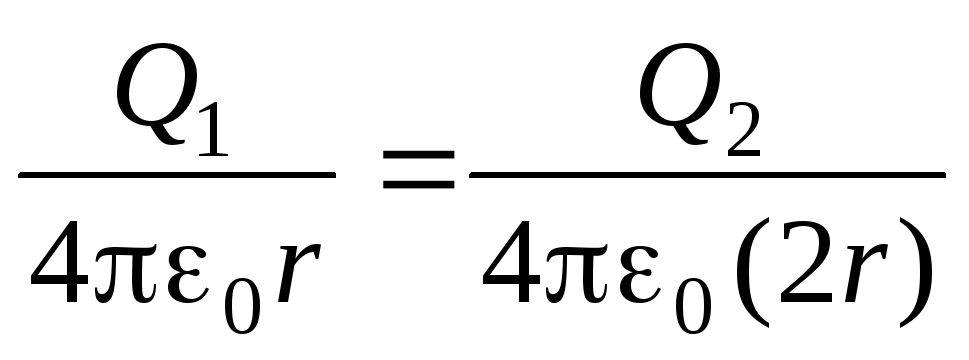i stałe ładunki piłek Q 1 i Q 2 powstają w wyniku przepływu ładunku z jednej kulki na drugą. W tym przypadku całkowity ładunek kulek pozostaje stały:

Z tych równań znajdujemy

,

.

Energia kulek przed ich połączeniem drutem jest równa

i po podłączeniu

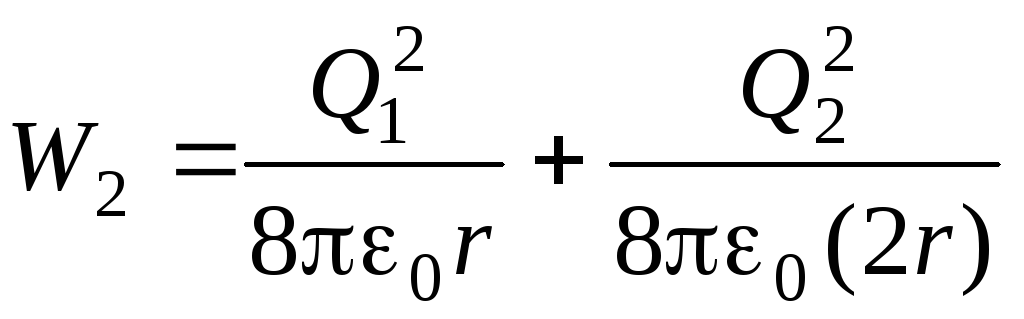Podstawianie wartości do ostatniego wyrażenia Q 1 i Q 2, otrzymujemy po prostych przekształceniach

Przykład 5.

Połączone w jedną kulę N= 8 identycznych kulek rtęci, z których każda ma ładunek Q. Zakładając, że w stanie początkowym kulki rtęci znajdowały się w dużej odległości od siebie, oblicz, ile razy wzrosła energia elektryczna układu.

Rozwiązanie.

Kiedy kule rtęci łączą się, ich całkowity ładunek i objętość zostają zachowane:

Gdzie Q– ładowanie piłki, R– jego promień, R jest promieniem każdej małej kulki rtęci. Całkowita energia elektryczna N pojedyncze kulki są równe

Energia elektryczna powstałej kuli

Po przekształceniach algebraicznych otrzymujemy

= 4.

Przykład 6.

Metalowa kula o promieniu R= 1 mm i ładunek Q= 0,1 nC Z duża odległość powoli zbliż się do nienaładowanego przewodnika i zatrzymaj się, gdy potencjał kuli zrówna się z  = 450 V. Ile pracy należy w tym celu wykonać?

Rozwiązanie.

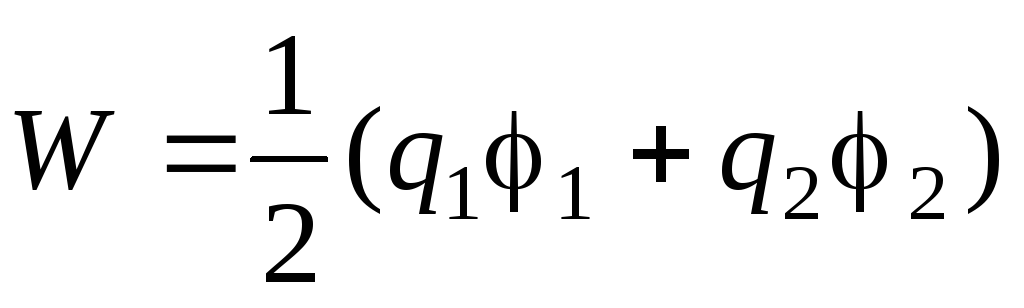Gdzie Q 1 i Q 2 – ładunki przewodników,  1 i  2 – ich potencjały. Ponieważ przewodnik zgodnie z problemem nie jest naładowany, zatem

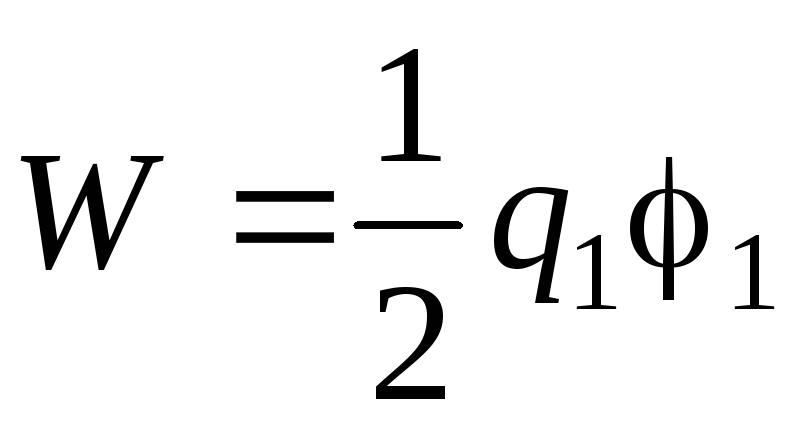Gdzie Q 1 i 1 ładunek i potencjał piłki. Kiedy kulka i nienaładowany przewodnik znajdują się w dużej odległości od siebie,

i energię elektryczną układu

W końcowym stanie układu, gdy potencjał kuli zrówna się z , energia elektryczna układu wynosi:

Praca sił zewnętrznych jest równa przyrostowi energii elektrycznej:

= –0,0225 µJ.

Zauważ to pole elektryczne w stanie końcowym układu tworzony jest przez ładunki indukowane w przewodniku, a także przez ładunki nierównomiernie rozmieszczone na powierzchni metalowej kulki. Bardzo trudno jest obliczyć to pole przy znanej geometrii przewodnika i zadanym położeniu metalowej kulki. Nie musieliśmy tego robić, ponieważ problem nie określa konfiguracji geometrycznej układu, ale potencjał kuli w stanie końcowym.

Przykład 7 .

System składa się z dwóch koncentrycznych cienkich metalowych osłon o promieniach R 1 i R 2 (

i odpowiednie opłaty Q 1 i Q 2. Znajdź energię elektryczną W systemy. Rozważmy także szczególny przypadek, w którym

.

Rozwiązanie.

Energię elektryczną układu dwóch naładowanych przewodników określa się ze wzoru

Aby rozwiązać problem, należy znaleźć potencjały sfery wewnętrznej ( 1) i zewnętrznej ( 2). Nie jest to trudne (patrz odpowiednia część instrukcji):

,

.

Podstawiając te wyrażenia do wzoru na energię, otrzymujemy

Na

energia jest równa

Energia elektryczna własna i energia interakcji

Przykład 8.

Dwie przewodzące kule, których ładunki Q I - Q, promienie R 1 i R 2 znajdują się w próżni w dużej odległości od siebie. Kula o większym promieniu R 2 składa się z dwóch półkul. Półkule są oddzielone i doprowadzone do kuli o promieniu R 1 i są ponownie połączone, tworząc w ten sposób kondensator sferyczny. Określ działanie sił elektrycznych za pomocą tej konstrukcji kondensatora.

Rozwiązanie.

Energia elektryczna dwóch naładowanych kul odległych od siebie jest równa

Energia elektryczna powstałego kondensatora sferycznego:

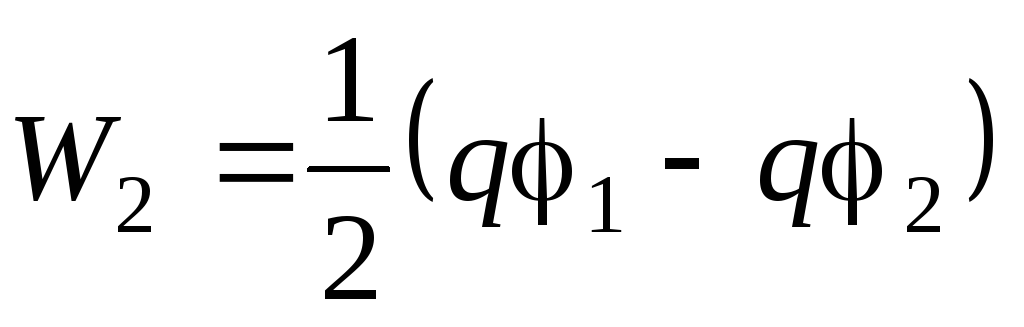Potencjał sfery wewnętrznej,

- potencjał sfery zewnętrznej. Stąd,

Praca sił elektrycznych przy tej konstrukcji kondensatora:

Należy pamiętać, że energia elektryczna kondensatora sferycznego W 2 jest równa pracy wykonanej przez siły zewnętrzne podczas ładowania kondensatora. W tym przypadku siły elektryczne działają

. Praca ta jest wykonywana nie tylko wtedy, gdy naładowane płyty zbliżają się do siebie, ale także wtedy, gdy do każdej z płytek zostanie przyłożony ładunek. Dlatego A EL różni się od pracy znalezionej powyżej A, udoskonalany siłami elektrycznymi tylko wtedy, gdy płyty się łączą.

Przykład 9.

Opłata punktowa Q= 1,5 µC znajduje się w środku kulistej powłoki, na powierzchni której ładunek jest równomiernie rozłożony Q= 5 µC. Znajdź pracę wykonaną przez siły elektryczne podczas rozszerzania się powłoki - jej promień zwiększa się z R 1 = 50 mm do R 2 = 100 mm.

Rozwiązanie.

Energia oddziaływania ładunku punktowego Q z ładunkami umieszczonymi na kulistej powłoce o promieniu R równy

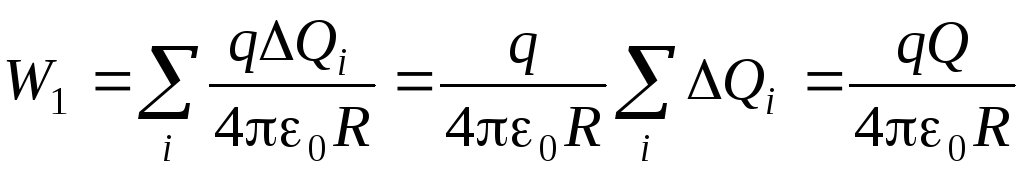Energia własna powłoki (energia wzajemnego oddziaływania ładunków powłoki) jest równa:

Praca sił elektrycznych podczas rozszerzania powłoki:

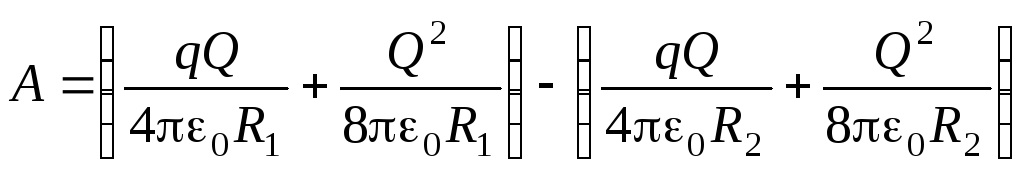Po przekształceniach otrzymujemy

1,8 J.

Inne rozwiązanie

Wyobraźmy sobie ładunek punktowy w postaci równomiernie naładowanej kuli o małym promieniu R i naładuj Q. Całkowita energia elektryczna układu jest równa

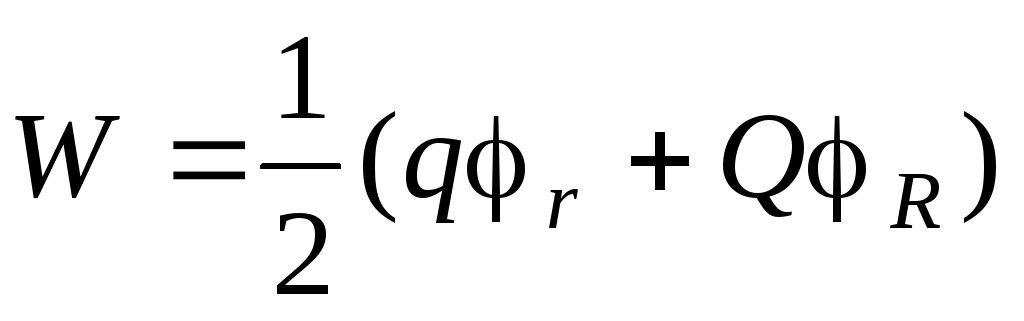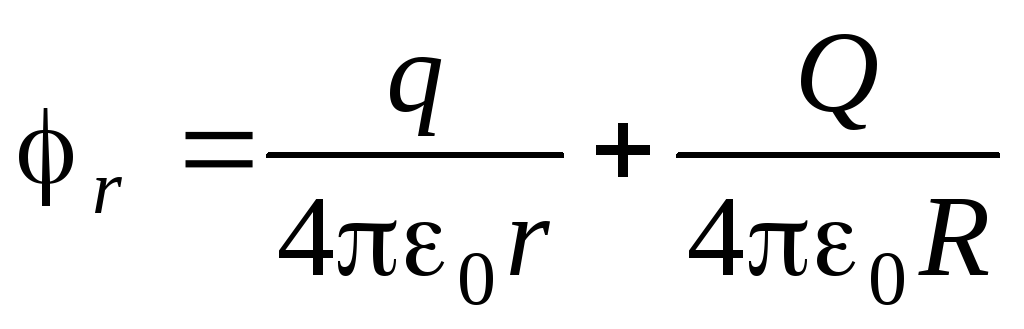
Potencjał sfery promienia R,

Potencjał sfery promienia R. Kiedy zewnętrzna kula rozszerza się, siły elektryczne działają

Po podstawieniach i przekształceniach otrzymujemy odpowiedź.

Wolumetryczna gęstość energii pola elektrycznego

Przykład 10 .

Jaka część energii elektrycznej naładowanej przewodzącej kuli znajdującej się w próżni zawarta jest w wyimaginowanej kuli koncentrycznej z kulą, której promień wynosi N razy promień kuli?

Rozwiązanie.

Wolumetryczna gęstość energii pola elektrycznego

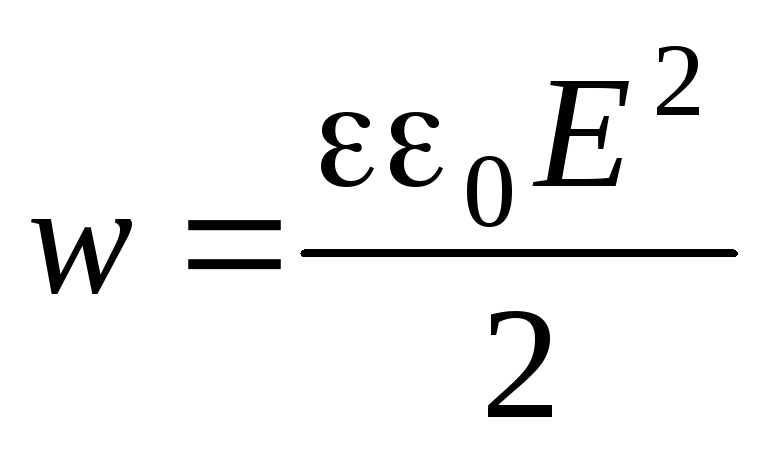
określa energię elektryczną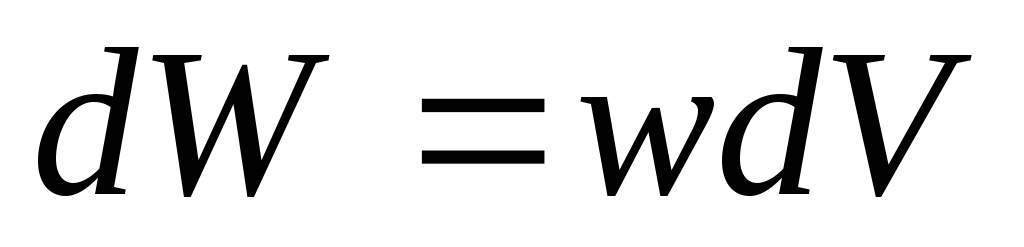

, zlokalizowane w nieskończenie małej objętości

(mi– moduł wektora natężenia pola elektrycznego w tej objętości,  – stała dielektryczna). Aby obliczyć całkowitą energię elektryczną naładowanej przewodzącej kuli, podzielmy w myślach całą przestrzeń na nieskończenie cienkie sferyczne warstwy koncentryczne z naładowaną kulą. Rozważmy jedną z tych warstw promienia R i grubość dr(patrz ryc. 5). Jego objętość jest

oraz energia elektryczna skupiona w warstwie

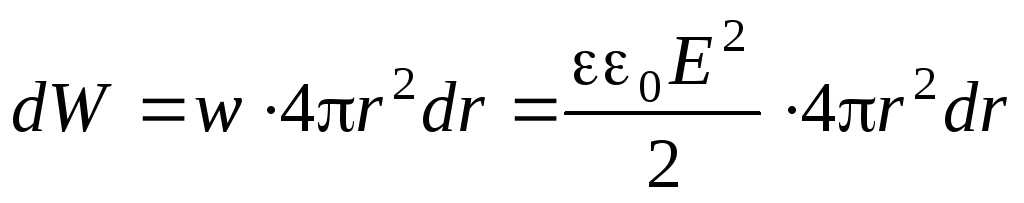Napięcie mi pole naładowanej przewodzącej kuli zależy, jak wiadomo, od odległości R do środka piłki. Wewnątrz piłki

dlatego przy obliczaniu energii wystarczy wziąć pod uwagę tylko te sferyczne warstwy, których promień R który przekracza promień kuli R.

Na

siła pola

przenikalność

i dlatego

Gdzie Q– ładowanie piłki.

Całkowita energia elektryczna naładowanej kuli jest określona przez całkę

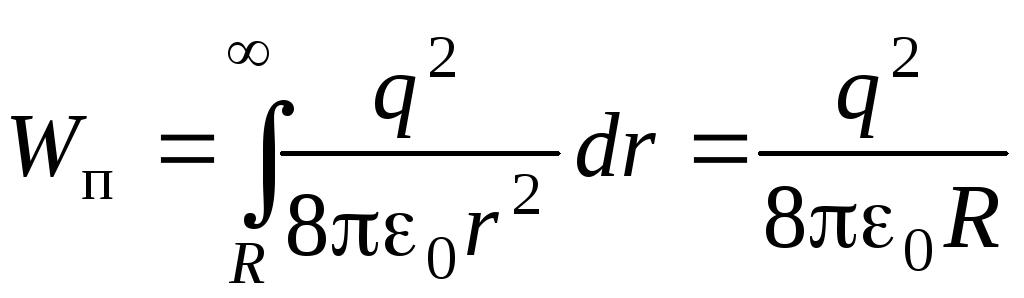a energia skoncentrowana wewnątrz wyimaginowanej kuli o promieniu nr, jest równe

Stąd,

Przykład 11.

Wyznacz energię elektryczną układu składającego się z naładowanej przewodzącej kuli i koncentrycznej z nią nienaładowanej przewodzącej sferycznej warstwy (rys. 6). Promienie wewnętrzne i zewnętrzne warstwy A I B, promień kuli

, opłata Q, system znajduje się w próżni.

Rozwiązanie.

Wewnątrz i powierzchnie zewnętrzne indukowane ładunki są rozmieszczone w warstwie kulistej. Ich suma algebraiczna wynosi zero, więc indukowane ładunki nie wytwarzają pola elektrycznego

, Gdzie R– odległość od środka układu. W okolicy

natężenie pola indukowanych ładunków również wynosi zero, ponieważ są one równomiernie rozmieszczone na powierzchniach kulistych. Zatem pole elektryczne układu pokrywa się z polem kuli równomiernie naładowanej na powierzchni, z wyjątkiem wewnętrznego obszaru warstwy kulistej, gdzie mi= 0. Rysunek 7 przedstawia przybliżony wykres zależności

. Pomijając szczegółowe obliczenia (patrz przykład 10), dla energii elektrycznej układu piszemy:

Gdzie

,

,

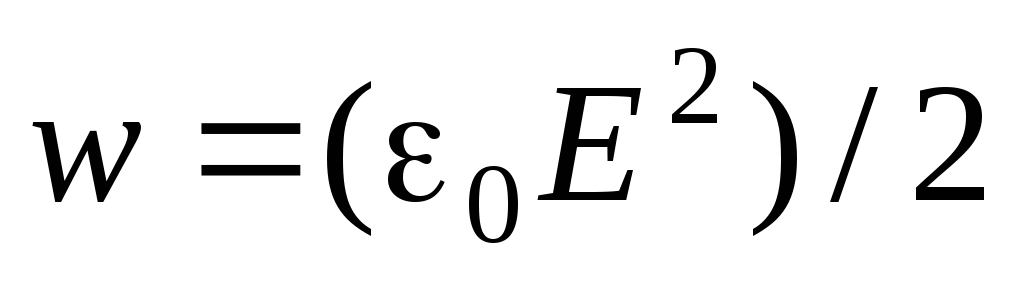. Po całkowaniu otrzymujemy

Przykład 12.

Opłata wstępna Q rozłożone równomiernie w objętości kuli o promieniu R. Następnie, na skutek wzajemnego odpychania, ładunki przemieszczają się na powierzchnię kuli. Jaką pracę wykonują siły elektryczne? Rozważ stałą dielektryczną równą jedności.

Rozwiązanie.

Praca sił elektrycznych jest równa utracie energii elektrycznej:

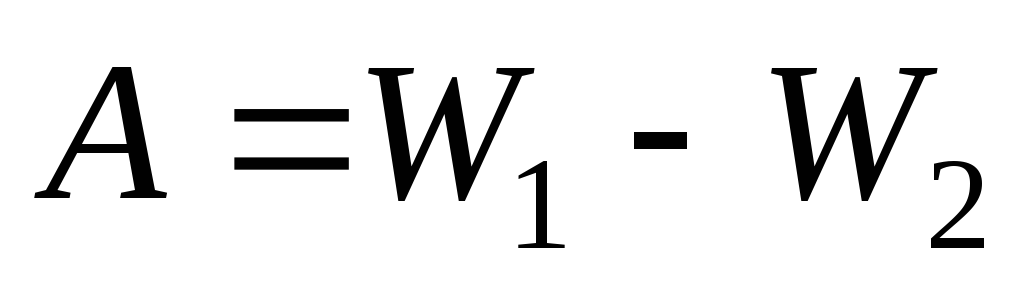Gdzie W 1 – energia elektryczna kuli naładowanej równomiernie w całej objętości, W 2 – energia tej samej kuli, równomiernie naładowanej na powierzchni. Ponieważ całkowity ładunek w obu przypadkach jest taki sam, pole elektryczne na zewnątrz kuli nie zmienia się, gdy ładunek przenosi się z objętości na powierzchnię. Pole elektryczne i energia zmieniają się tylko wewnątrz kuli.

Korzystając z twierdzenia Gaussa, możemy wyprowadzić wzór na natężenie pola wewnątrz równomiernie naładowanej kuli znajdującej się w odległości R od jego środka:

Energię elektryczną skupioną wewnątrz kuli określa całka:

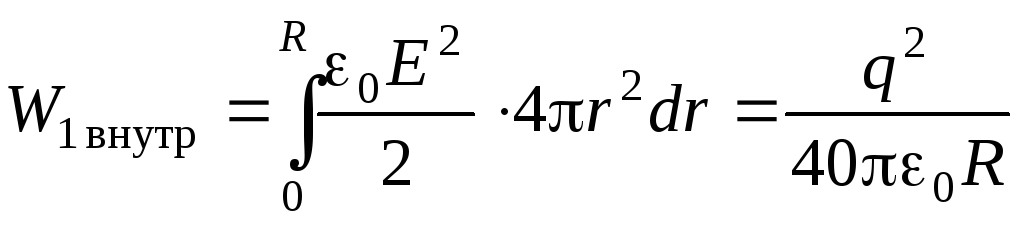Kiedy wszystkie ładunki przeniosły się na powierzchnię kuli, pole elektryczne, a co za tym idzie, energia pola elektrycznego wewnątrz kuli, osiągnęły wartość zerową. Zatem,

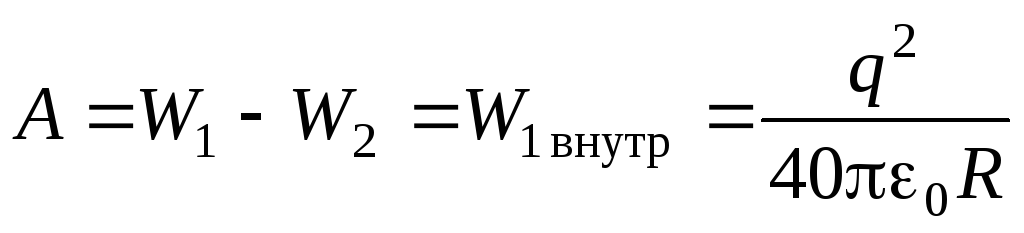Jednym z najciekawszych i najbardziej przydatnych odkryć w mechanice jest prawo zachowania energii. Znając wzory na energię kinetyczną i potencjalną układu mechanicznego, jesteśmy w stanie wykryć związek pomiędzy stanami układu w dwóch różnych momentach czasu, bez wnikania w szczegóły tego, co dzieje się pomiędzy tymi momentami. Chcemy teraz wyznaczyć energię układów elektrostatycznych. W elektryczności zasada zachowania energii okaże się równie przydatna w odkrywaniu wielu interesujących faktów.

Prawo, według którego zmienia się energia podczas oddziaływania elektrostatycznego, jest bardzo proste; właściwie już o tym rozmawialiśmy. Niech będą ładunki i oddzielone przerwą. Układ ten ma pewną energię, ponieważ połączenie ładunków wymagało pewnej pracy. Obliczyliśmy pracę wykonaną, gdy dwa ładunki zbliżają się do siebie z dużej odległości; jest równe

Z zasady superpozycji wiemy, że jeśli ładunków jest wiele, to całkowita siła działająca na którykolwiek z ładunków jest równa sumie sił działających na wszystkie pozostałe ładunki. Wynika z tego, że całkowita energia układu kilku ładunków jest sumą wyrazów wyrażających oddziaływanie każdej pary ładunków z osobna. Jeśli i są dwoma ładunkami i odległością między nimi (ryc. 8.1), wówczas energia tej konkretnej pary jest równa

Rysunek 8.1. Energia elektrostatyczna układu cząstek jest sumą energie elektrostatyczne każda para

Całkowita energia elektrostatyczna jest sumą energii wszystkich możliwych par ładunków:

(8.3)

Jeśli rozkład jest określony przez gęstość ładunku , wówczas sumę z (8.3) należy oczywiście zastąpić całką.

O energii będziemy tutaj mówić z dwóch perspektyw. Pierwszym z nich jest zastosowanie koncepcji energii do problemów elektrostatycznych; drugi - różne sposoby szacunki energetyczne. Czasami łatwiej jest obliczyć wykonaną pracę w jakimś przypadku niż oszacować wartość sumy w (8.3) lub wartość odpowiedniej całki. Dla próbki obliczamy energię potrzebną do złożenia równomiernie naładowanej kuli z ładunków. Energia to tutaj nic innego jak praca włożona w zbieranie ładunków z nieskończoności.

Wyobraź sobie, że budujemy kulę, układając kolejno jedna na drugiej sferyczne warstwy o nieskończenie małej grubości. Na każdym etapie procesu zbieramy niewielką ilość prądu i umieszczamy go cienką warstwą od do. Kontynuujemy ten proces, aż osiągniemy zadany promień (ryc. 8.2). Jeżeli ładunek znajduje się na kuli w chwili, gdy kula osiągnie promień , to praca potrzebna do dostarczenia ładunku kuli jest równa

Rysunek 8.2. Energię równomiernie naładowanej kuli można obliczyć, wyobrażając sobie, że została ona uformowana poprzez kolejne nakładanie na siebie sferycznych warstw.

Jeżeli gęstość ładunku wewnątrz kuli wynosi , wówczas ładunek jest równy

a ładunek jest równy we wszystkich parach punktów wewnątrz kuli.

Pozwalać ładunek elektryczny Q równomiernie rozłożone na powierzchni kuli o promieniu R. Poza kulą pole elektryczne wytworzone przez ładunki na kuli jest równoważne polu ładunku punktowego umieszczonego w środku kuli (ryc. 350).

ryż. 350
Wewnątrz kuli nie ma pola. Zatem natężenie pola w punkcie znajdującym się w dużej odległości R od środka kuli jest równa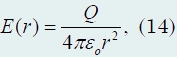

w szczególności bezpośrednio na powierzchni kuli natężenie pola wynosi
(15)
Należy pamiętać, że praca S = 4πR2 jest obszarem kuli, a następnie stosunkiem

jest gęstością ładunku powierzchniowego na kuli, zatem natężenie pola na powierzchni kuli wyraża się tym samym wzorem, co natężenie pola między płytami omówione w poprzedniej sekcji E o = σ/ε o. Potencjał powierzchniowy kuli również obliczyliśmy wcześniej

Obliczmy teraz energię pola wytworzonego przez ładunki na kuli. Podziel mentalnie ładunek kuli na N równe małe części, których rozmiary są równe

Rozważmy jeden z tych małych ładunków. W miejscu jego lokalizacji potencjał pola tworzony jest przez wszystkie pozostałe (N - 1) opłaty są równe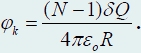

Korzystanie ze wzoru symetrycznego

wyrażenie na energię interakcji przyjmuje formę

ta ilość zawiera N identyczne terminy, a zatem równe

Od ilości części N, na który podzielona jest kula, można dowolnie powiększyć, a następnie w granicach N → ∞ termin 1/N znika, dlatego ostateczne wyrażenie na energię oddziaływania ładunków kuli ma postać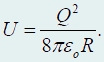

Należy pamiętać, że wynikowe wyrażenie ma postać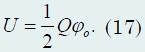

Jeśli od razu stwierdzimy, że zmniejszenie opłaty o mała ilość δQ zmienia w pomijalnym stopniu potencjał kuli, to wynik (17) otrzymujemy poprzez bezpośrednie zastosowanie wzoru na energię oddziaływania ładunków. Jednakże obchodzenie się z małymi ilościami wymaga pewnego rygoru, dlatego podaliśmy nieco „wydłużony” wniosek.
Przedstawmy inny wniosek z tego samego formuła 1. Aby to zrobić, obliczamy energię układu jako pracę, jaką należy wykonać, aby naładować kulę.

Będziemy mentalnie ładować kulę małymi, równymi porcjami ładunku które przeniesiemy na kulę z „nieskończoności”. Jeśli kula nie jest naładowana, to przeniesienie pierwszej „porcji” ładunku nie wymaga wykonania żadnej pracy. Gdy kula nabierze określonego ładunku elektrycznego, przeniesienie kolejnej porcji ładunku wymaga pracy, aby pokonać siły odpychające pochodzące od ładunków kuli. Jeśli zostanie przeniesiony do kuli(k - 1)

część ładunku, wówczas jego potencjał jest równy

Aby więc przenieść kolejną porcję ładunku na kulę, należy wykonać pracę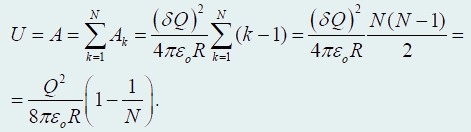

Całkowitą pracę wykonaną podczas ładowania kuli (równą energii pola elektrycznego kuli) wyraża się sumą postępu geometrycznego
Zgodnie z oczekiwaniami otrzymaliśmy wyrażenie całkowicie pokrywające się z (17); przy nieskończonym zmniejszaniu się części przenoszonych ładunków ponownie dochodzimy do wzoru (14).
Nie jest to zaskakujące, ponieważ w pierwszym przypadku obliczyliśmy energię, która zostanie uwolniona, gdy ładunki rozproszą się z kuli, a w drugim przypadku energię, którą należy wydać, aby je zebrać. Pokażmy, że energię oddziaływania ładunków w tym przypadku można interpretować także jako energię pola elektrycznego, „rozpływającą się” po całej przestrzeni, w której to pole występuje. Wyobraźmy sobie, że promień kuli wzrósł o niewielką wartośćΔR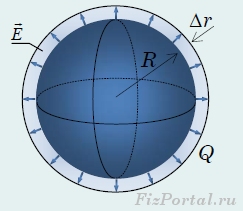

, ale jego ładunek się nie zmienił. Zgodnie ze wzorem (14) energia oddziaływania ładunków będzie się zmniejszać. W przestrzeni poza sferą o zwiększonym promieniu pole elektryczne nie uległo zmianie, natomiast w cienkiej warstwie sferycznej pomiędzy sferą początkową a rozszerzoną zanikło (ryc. 351).
ryż. 351

Należy zatem przyjąć, że spadek energii oddziaływania ładunków wraz ze wzrostem promienia kuli jest równy energii zawartej w tej cienkiej warstwie kulistej. Jeżeli grubość warstwy jest mała, jej objętość można obliczyć jako iloczyn pola powierzchni kuli i grubości warstwy

Pomijając zmianę natężenia pola w cienkiej warstwie, energię w niej zawartą zapisujemy w postaci Gdzie w

− gęstość energii pola. Natomiast energia ta jest równa zmianie energii oddziaływania ładunków wraz ze wzrostem promienia kuli NA ostatni krok Pokażmy, że energię oddziaływania ładunków w tym przypadku można interpretować także jako energię pola elektrycznego, „rozpływającą się” po całej przestrzeni, w której to pole występuje. Wyobraźmy sobie, że promień kuli wzrósł o niewielką wartość zaniedbaliśmy małą zmianę promienia

. Na koniec wyrażamy ładunek kuli w kategoriach natężenia pola elektrycznego na jej powierzchni

Z porównania ze wzorem (16) wynika, że w rozpatrywanym przypadku gęstość energii pola elektrycznego wyraża się wzorem