Densidade de energia do campo elétrico volumétrico
14.1. Energia de um sistema de cargas pontuais
Arroz. 14.1
A partir de uma comparação de (14.1) e (14.2) fica claro que P 1 P 2 , portanto a energia de um sistema de duas cargas pontuais pode ser representada de forma simétrica:
onde eu– potencial de campo criado por todas as cargas, exceto eu th, no ponto onde está localizado eu-ª cobrança.
^
14.2. Energia de um condutor carregado
Uma carga localizada na superfície de um condutor pode ser considerada como um sistema de cargas pontuais, portanto, para calcular a energia de um condutor carregado, pode-se usar a fórmula (14.4). O potencial de qualquer ponto na superfície do condutor é o mesmo ( eu=), pois sua superfície é equipotencial. Portanto, na fórmula (14.4) o potencial pode ser retirado do sinal de soma:
 ou
ou  , (14.5) onde
, (14.5) onde 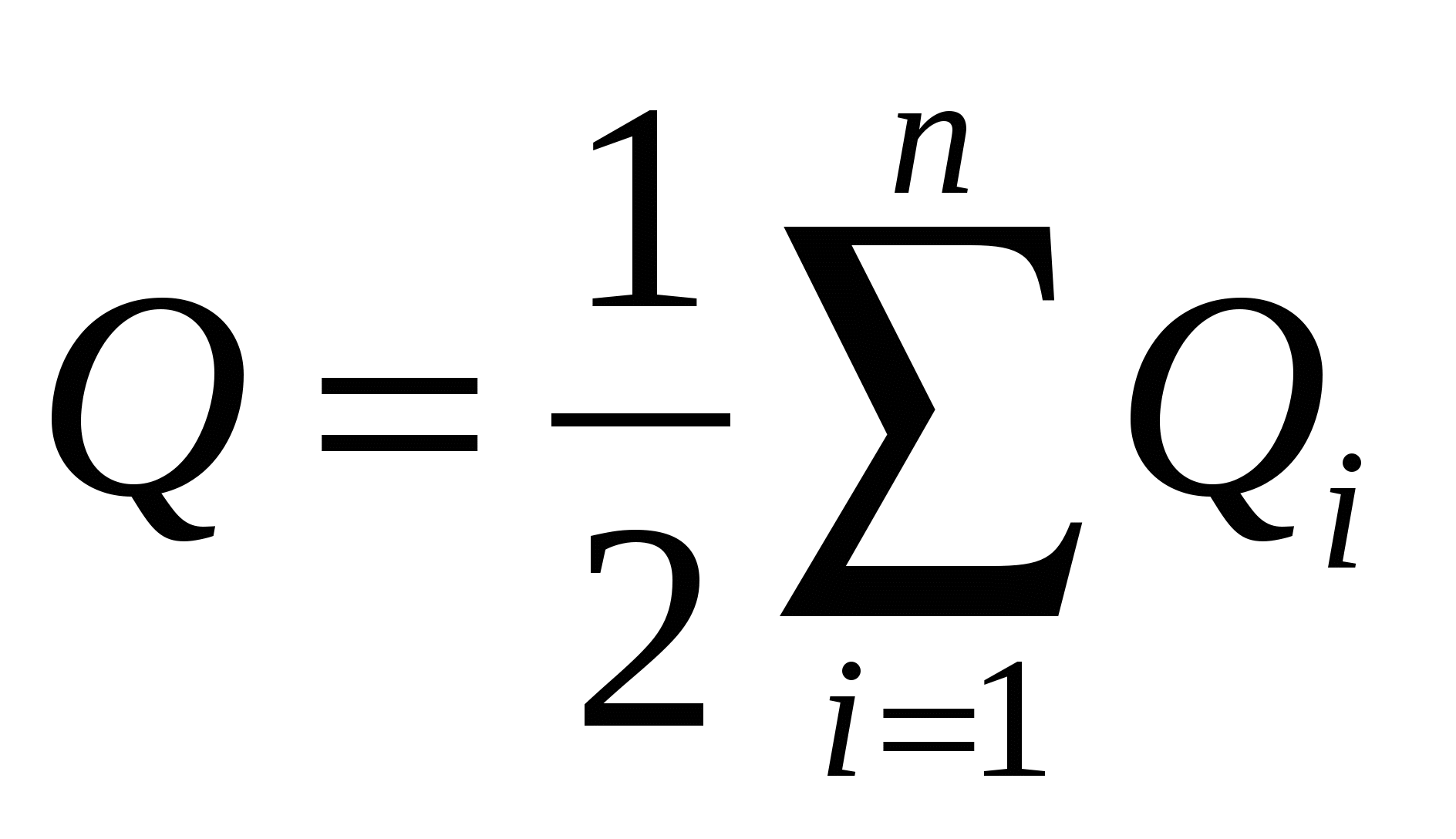 – carga do condutor.
– carga do condutor.
Levando em consideração (13.3), a expressão para a energia de um condutor carregado pode ser representada na forma
^
14.3. Energia de um capacitor carregado. Densidade de energia do campo eletrostático
Para calcular a energia de um capacitor carregado, usamos as fórmulas (14.5) – (14.7), substituindo pela diferença de potencial entre as placas do capacitor você = . Então
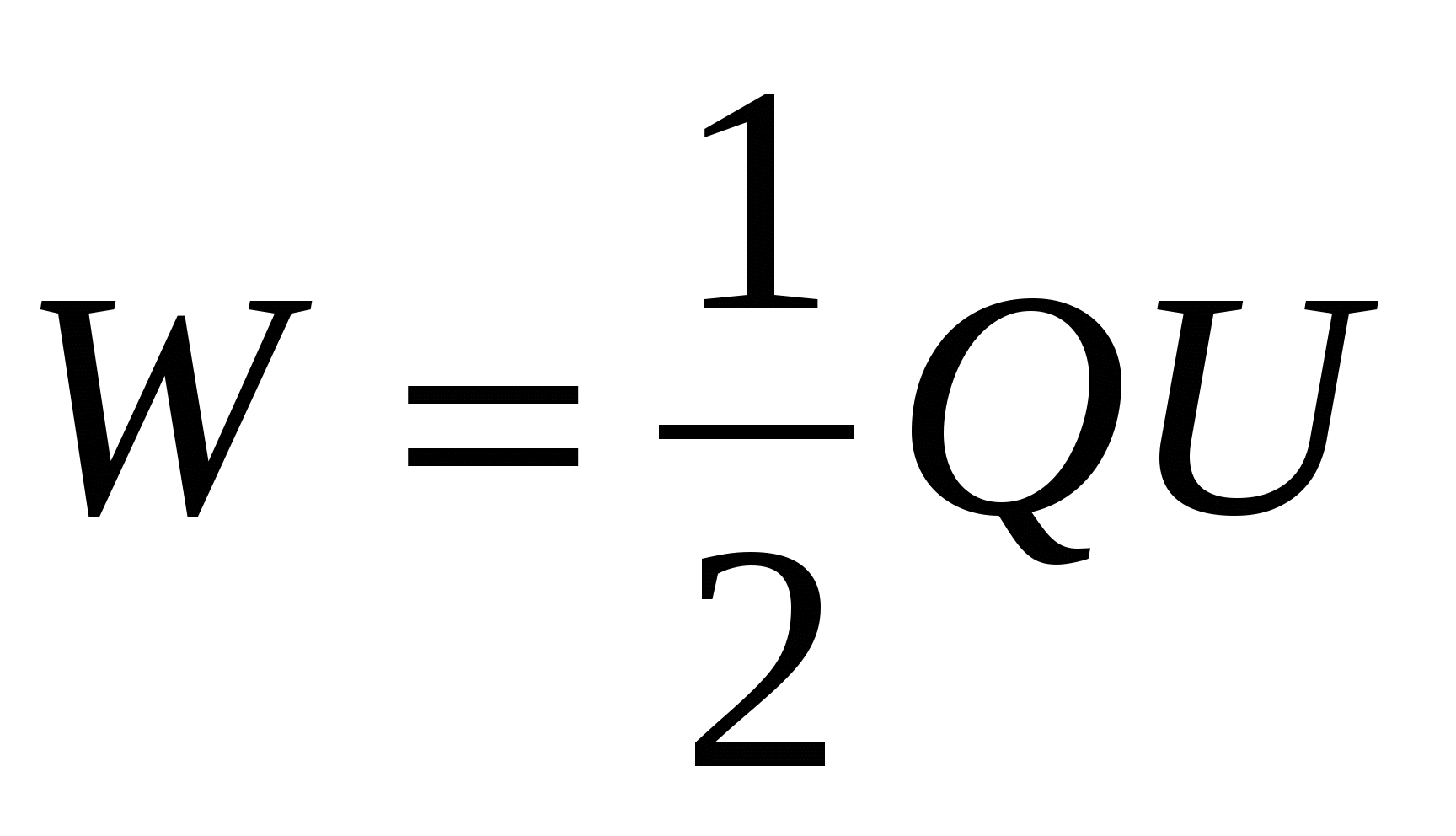 , , | (14.8) |
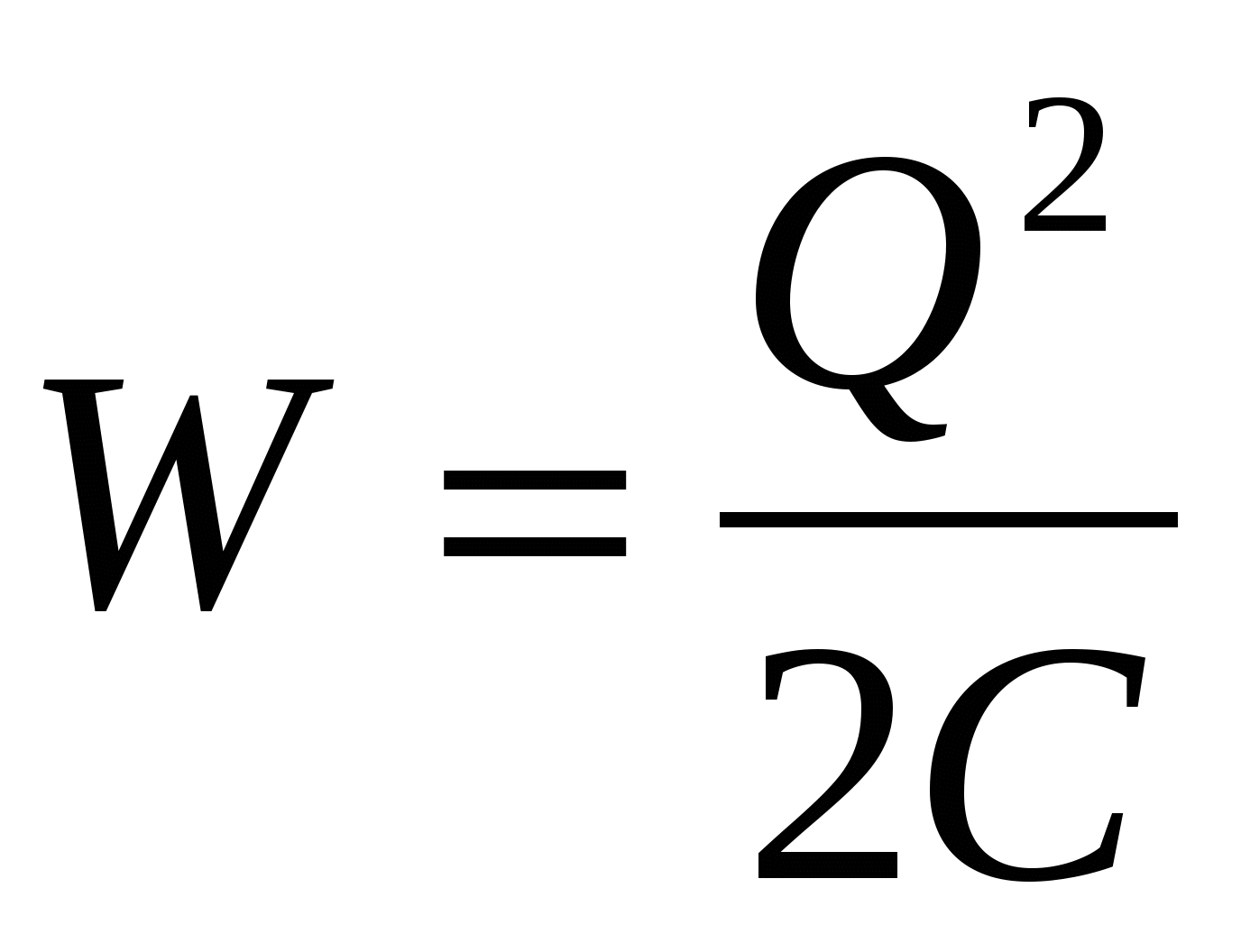 | (14.9) |
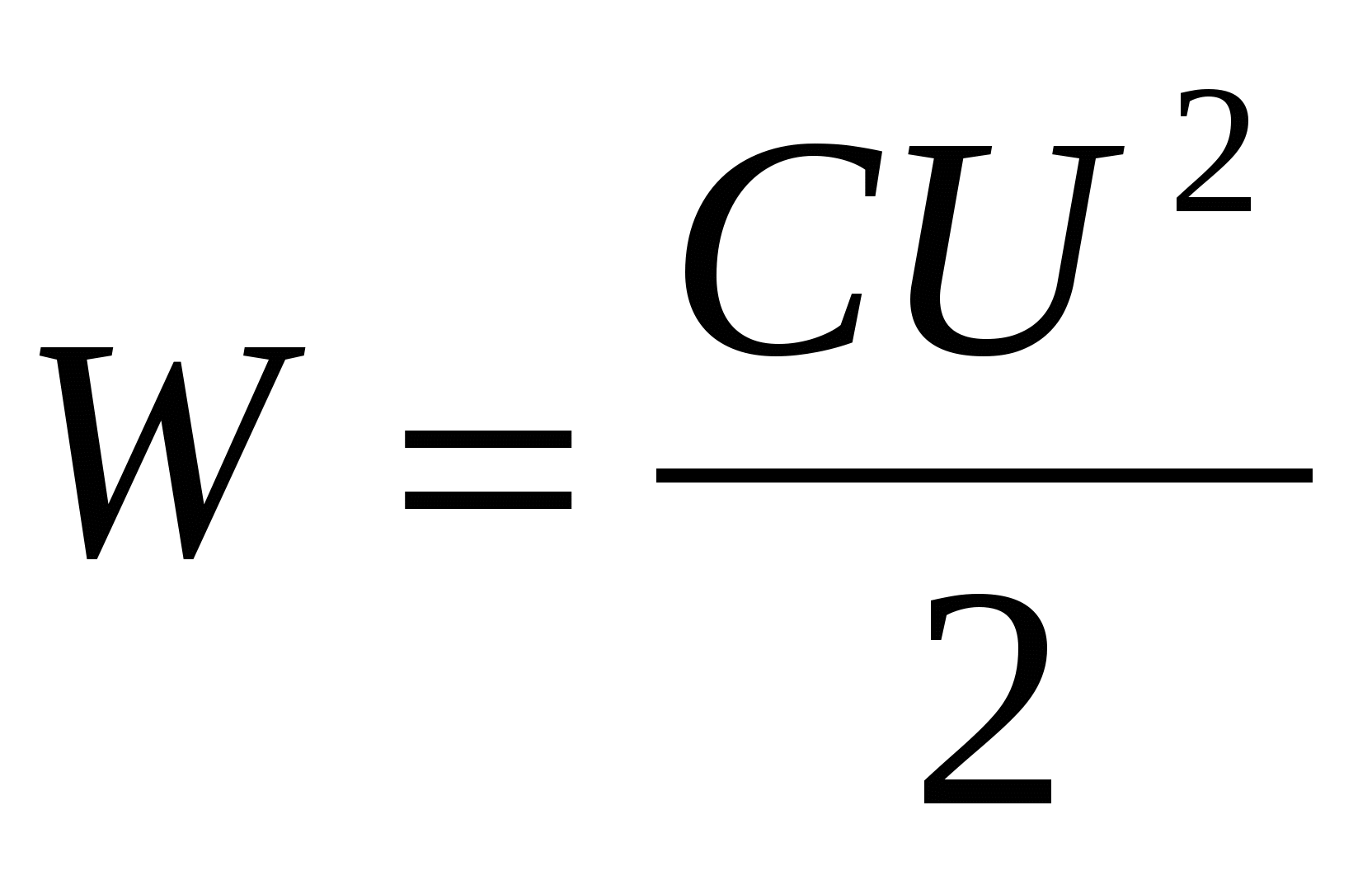 | (14.10) |
Faremos considerações adicionais com base na fórmula (14.9). Vamos imaginar a carga do capacitor como Q = S, onde é a densidade de carga superficial, e S– área da placa do capacitor. Utilizando ainda a expressão para a capacitância de um capacitor plano (13.7), apresentamos (14.9) na forma
Na fórmula (14.9), a energia de um capacitor carregado é expressa em termos da carga em suas placas e da capacitância. Na fórmula (14.12), a energia do capacitor é expressa em termos da tensão campo eletrostático, concentrado entre suas placas. Nesse sentido, surge a questão fundamental sobre o que serve de portador da energia do capacitor: cargas ou um campo eletrostático. Esta questão é central para o debate de longa data entre os proponentes de ações de longo e curto alcance.
Os defensores da ação de longo alcance preferiram a fórmula (14.9), considerando-a como a energia potencial de interação de dois corpos. Os defensores desta teoria rejeitaram a possibilidade de interação através do campo.
Os proponentes da teoria de curto alcance (teoria de campo) acreditavam que a energia do capacitor é a energia do campo eletrostático (fórmula (14.2)). Essa energia fica “espalhada” por todo o volume do capacitor e, portanto, podemos falar em densidade volumétrica de energia:
 [J/m 3 ] ou
[J/m 3 ] ou 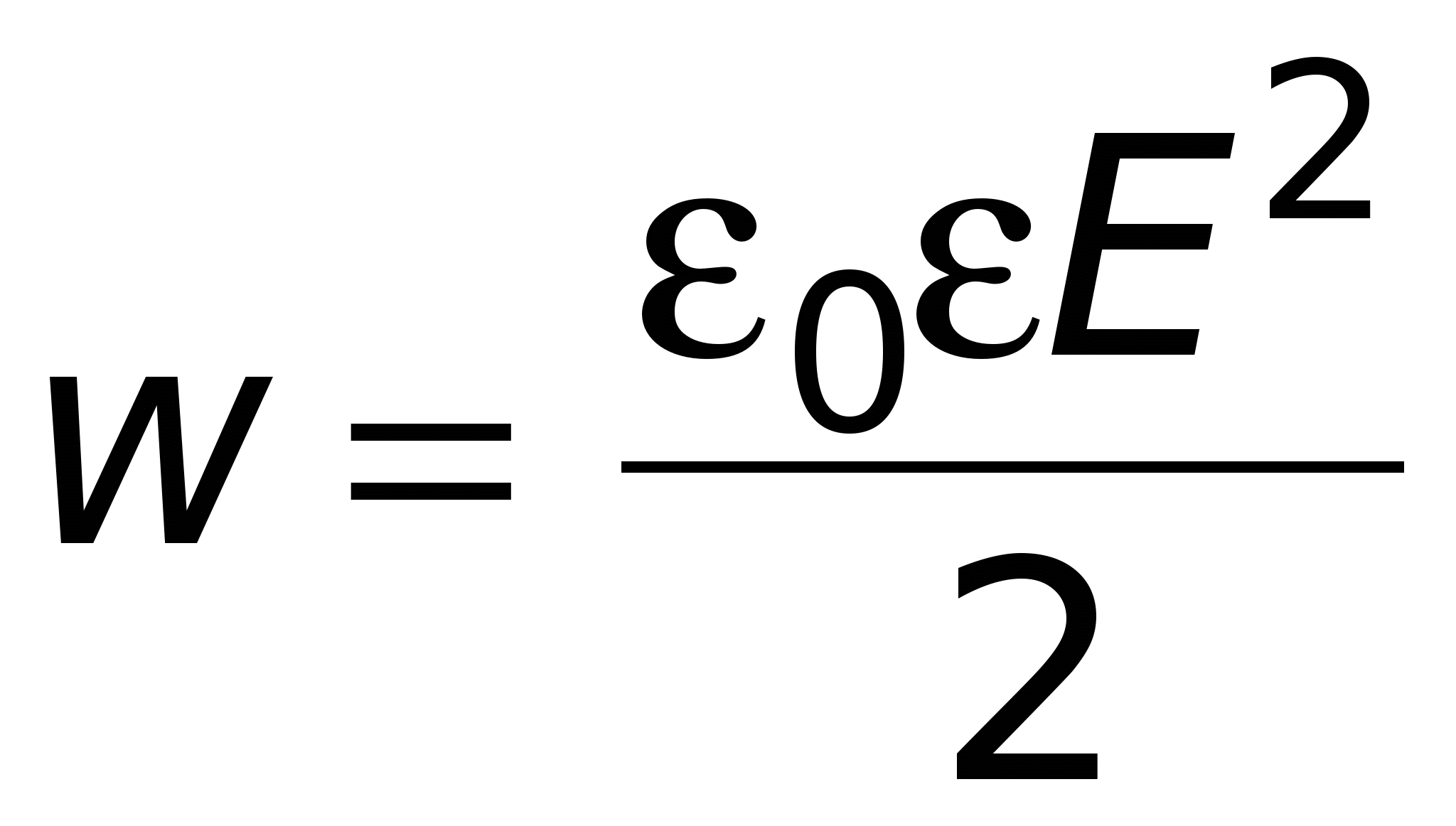 , Levando em consideração (12.11), a fórmula (14.13) pode ser representada na forma
, Levando em consideração (12.11), a fórmula (14.13) pode ser representada na forma
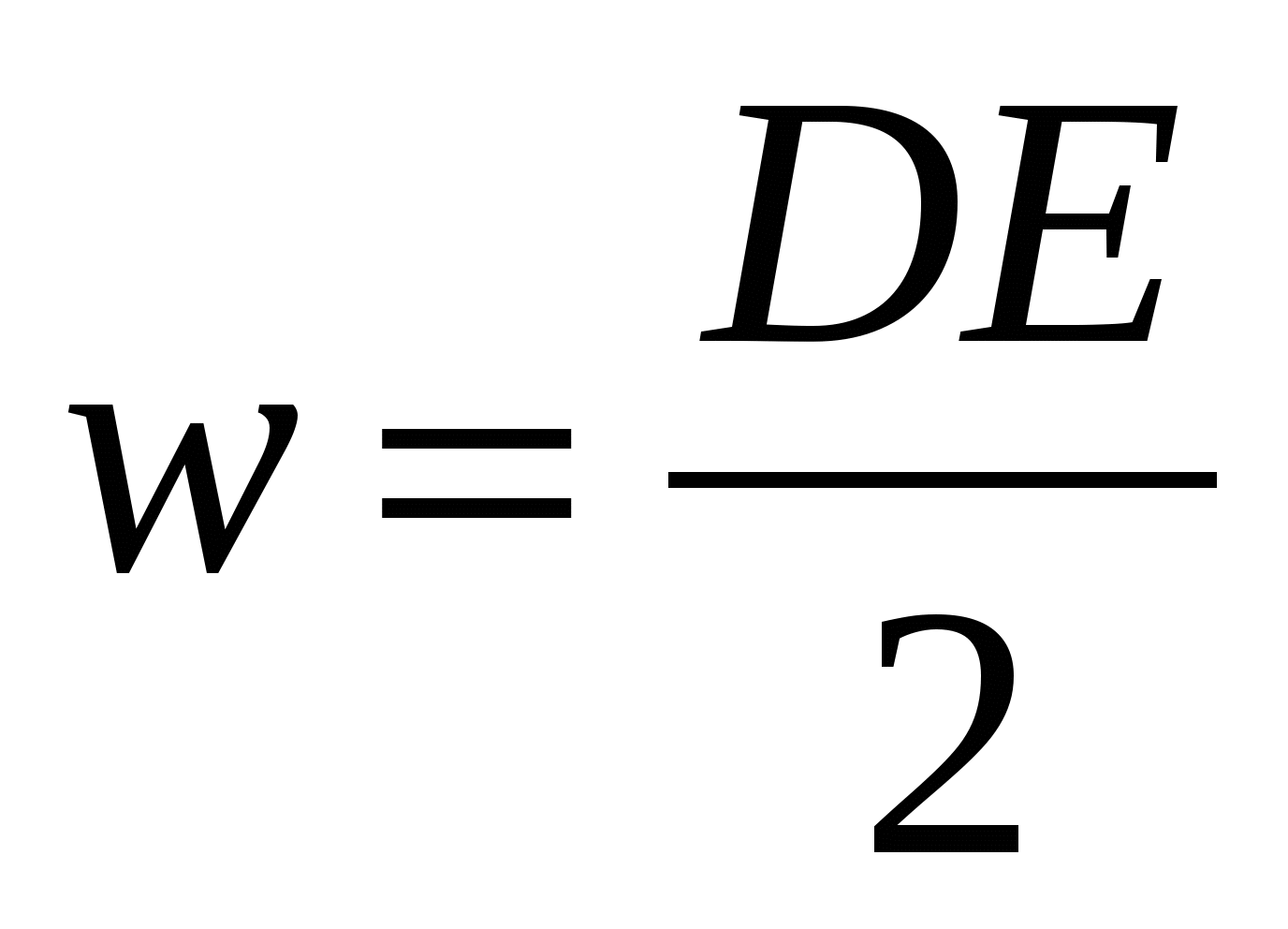 | (14.14) |
No âmbito da eletrostática, é impossível resolver a questão de qual é o portador de energia – cargas ou um campo, uma vez que as cargas estacionárias e o campo eletrostático que elas criam são inseparáveis. Ao estudar campos elétricos e magnéticos alternados, descobriu-se que o campo eletromagnético pode ser separado de cargas que existem independentemente delas. Este é o argumento decisivo a favor da teoria da acção de curto alcance (teoria de campo).
Aula 23.
15. Permanente eletricidade
^
15.1. Força e densidade atuais
A corrente elétrica é o movimento ordenado (direcionado) de micropartículas carregadas ou corpos macroscópicos carregados. A direção da corrente é considerada a direção do movimento das cargas positivas; se a corrente for criada por partículas carregadas negativamente (por exemplo, elétrons), então a direção da corrente é oposta à direção do movimento das partículas. É feita uma distinção entre corrente de condução (movimento direcionado de partículas carregadas dentro de um corpo macroscópico) e corrente de convecção (movimento de um corpo carregado como um todo). A seguir consideraremos apenas a corrente de condução.
Quantitativamente, a corrente elétrica é caracterizada por uma quantidade escalar: intensidade da corrente EU e quantidade vetorial – densidade de corrente elétrica 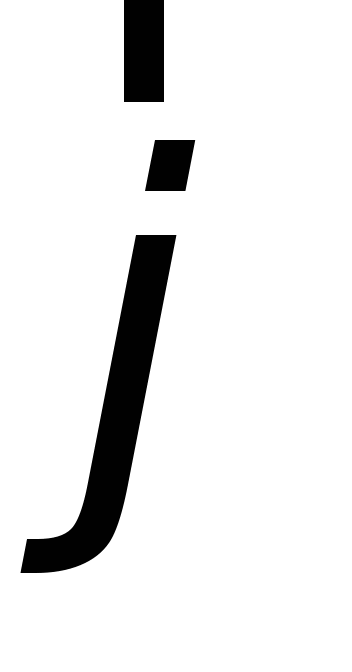 .
.
A intensidade da corrente é numericamente igual à carga que passa pela seção transversal do condutor por unidade de tempo:
onde o sinal "" indica que o site 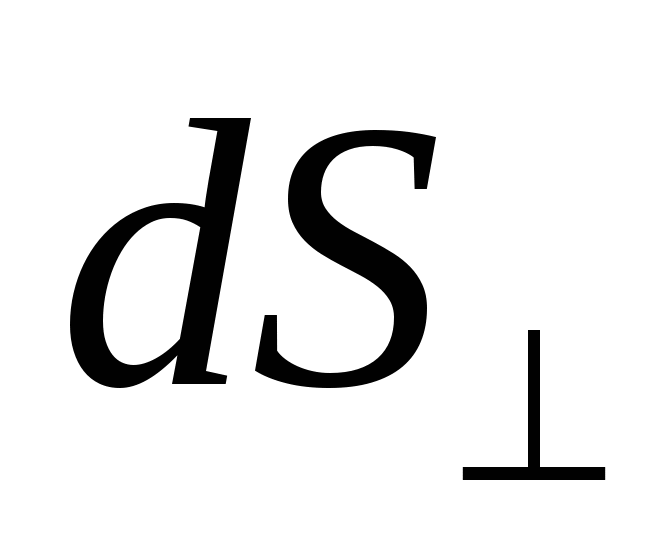 orientado perpendicularmente à direção da corrente. A direção do vetor coincide com a direção do movimento das cargas positivas.
orientado perpendicularmente à direção da corrente. A direção do vetor coincide com a direção do movimento das cargas positivas.
Vamos encontrar uma expressão para o vetor densidade de corrente em metais nos quais os portadores de corrente são elétrons livres. Sob a influência campo elétrico elétrons em um metal se movem em uma direção a uma velocidade média 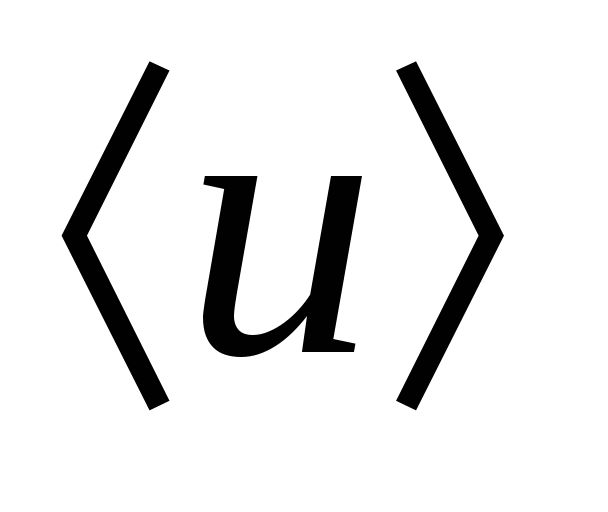 . Em uma unidade de tempo, através de uma unidade de área da seção transversal de um condutor passará n elétrons, onde n– número de elétrons por unidade de volume (concentração). Isso transferirá a cobrança pt. Portanto, a densidade de corrente
. Em uma unidade de tempo, através de uma unidade de área da seção transversal de um condutor passará n elétrons, onde n– número de elétrons por unidade de volume (concentração). Isso transferirá a cobrança pt. Portanto, a densidade de corrente
 . . | (15.3) |
15.2. Condições para a existência de corrente. Forças externas. CEM
Se o vetor de densidade de corrente não mudar ao longo do tempo, nem em magnitude nem em direção, essa corrente será chamada de constante. Vamos encontrar as condições de existência corrente direta.

Arroz. 15.1
Suponhamos que uma diferença de potencial seja criada nas extremidades do condutor  , e
, e 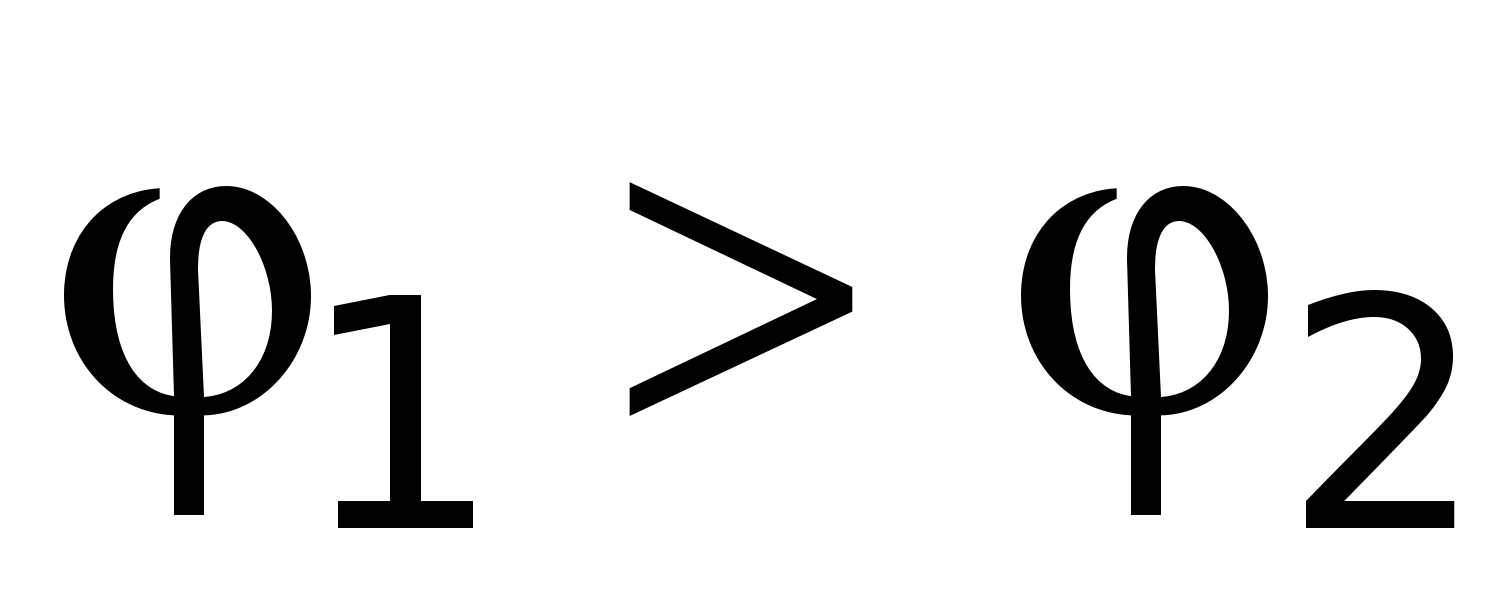 (Fig. 15.1). Neste caso, surgirá uma corrente de curto prazo no condutor, causada pelo movimento ordenado das cargas na direção do potencial decrescente (presume-se que os portadores de corrente tenham carga positiva). A corrente existirá até que os potenciais sejam equalizados nas extremidades do condutor. Para que a corrente permaneça constante por muito tempo, é necessário retirar cargas da extremidade do condutor com menor potencial até a extremidade do condutor com maior potencial, ou seja, realizar a circulação de carga. A este respeito, o circuito deve ser fechado.
(Fig. 15.1). Neste caso, surgirá uma corrente de curto prazo no condutor, causada pelo movimento ordenado das cargas na direção do potencial decrescente (presume-se que os portadores de corrente tenham carga positiva). A corrente existirá até que os potenciais sejam equalizados nas extremidades do condutor. Para que a corrente permaneça constante por muito tempo, é necessário retirar cargas da extremidade do condutor com menor potencial até a extremidade do condutor com maior potencial, ou seja, realizar a circulação de carga. A este respeito, o circuito deve ser fechado.
As forças eletrostáticas não podem garantir tal circulação de cargas, uma vez que na seção do circuito mostrada na Fig. 15.1 linha pontilhada, você precisa trabalhar contra o campo eletrostático. O movimento das cargas na direção do potencial crescente só é possível com a ajuda de forças adicionais de origem não eletrostática, chamadas forças externas. Essas forças podem ser fornecidas por processos químicos (células galvânicas), campos elétricos parasitas (geradores CA ou CC), etc.
Ao contrário das forças eletrostáticas, o trabalho realizado por forças externas para mover uma carga num círculo fechado é diferente de zero. Força eletromotriz(EMF) é o trabalho realizado por forças externas para mover uma única carga positiva ao longo do circuito, 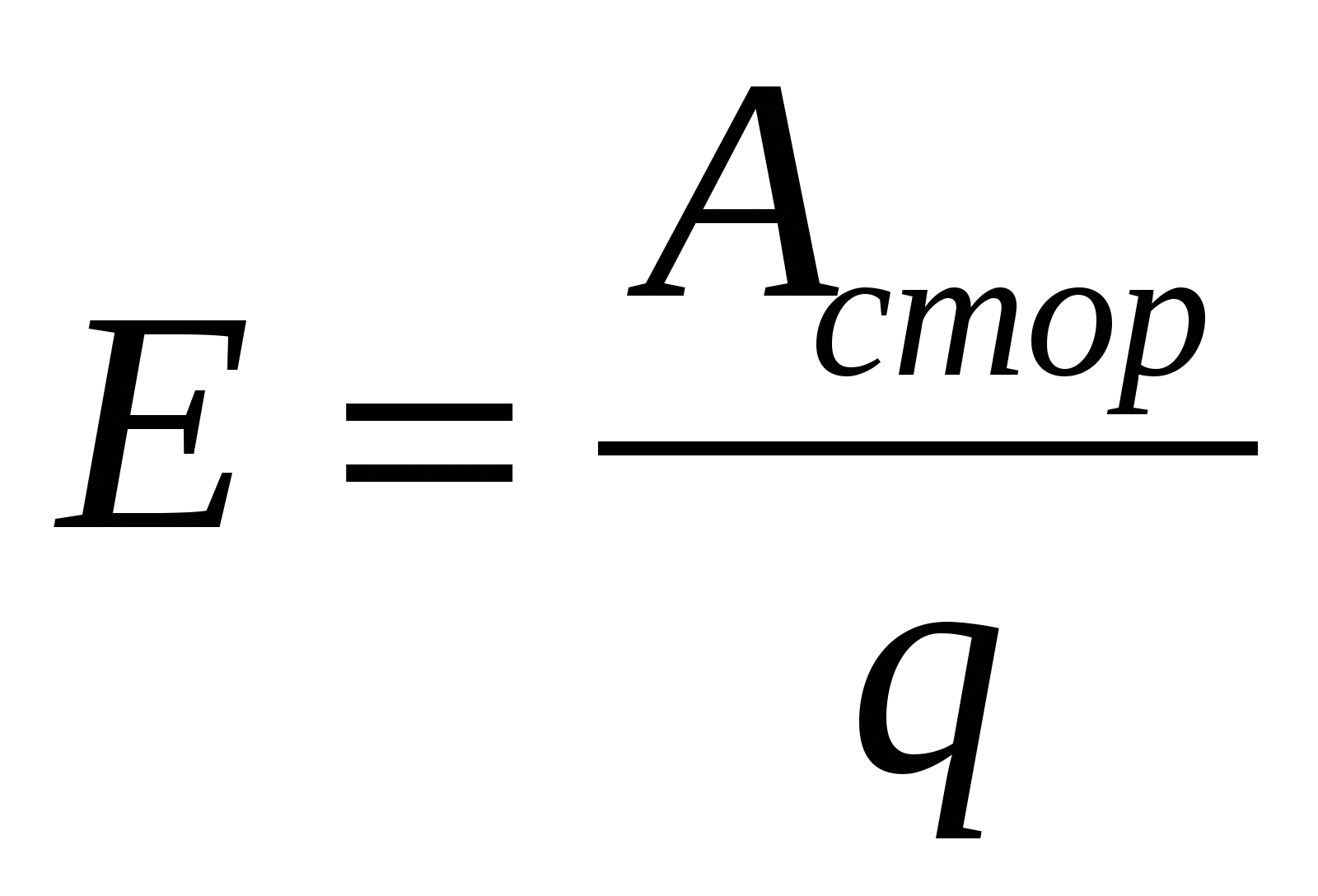 , (15.4) Assim como a diferença de potencial, a EMF é medida em volts.
, (15.4) Assim como a diferença de potencial, a EMF é medida em volts.
Vamos considerar um trecho do circuito onde, além das forças externas, atuam as forças eletrostáticas. Então o trabalho para mover a carga nesta área será igual à soma do trabalho: 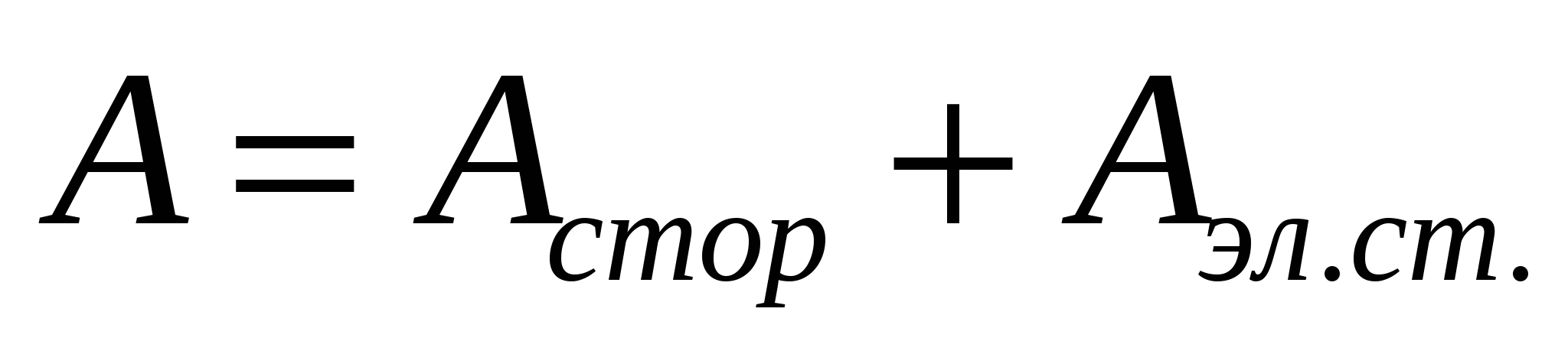
Vamos dividir esta expressão pela carga q:
O trabalho total realizado por forças externas e eletrostáticas para mover uma única carga positiva em uma determinada seção do circuito é chamado de tensão ou queda de tensão:
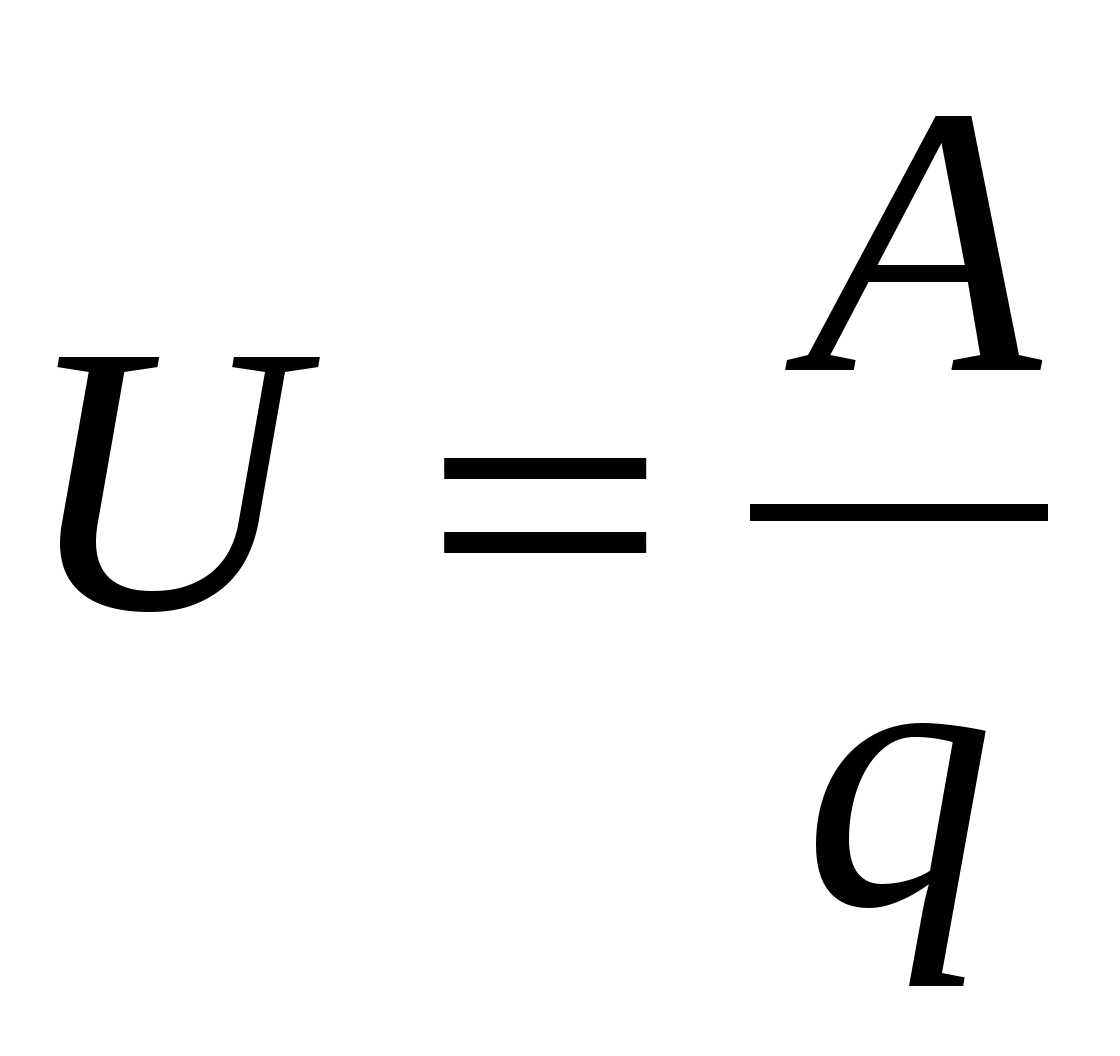 . . | (15.7) |
Substituindo (15.4), (15.6) e (15.7) em (15.5), obtemos a relação entre tensão, fem e diferença de potencial você=E + ( 1 - 2 )
De (15.8) fica claro que a tensão você igual à soma algébrica da fem e da diferença de potencial em uma determinada seção do circuito.
^
15.3. Lei de Ohm
15.3.1. Lei de Ohm para uma seção não uniforme de um circuito
Ohm estabeleceu experimentalmente que a intensidade da corrente em uma determinada seção do circuito é proporcional à tensão e inversamente proporcional à resistência: 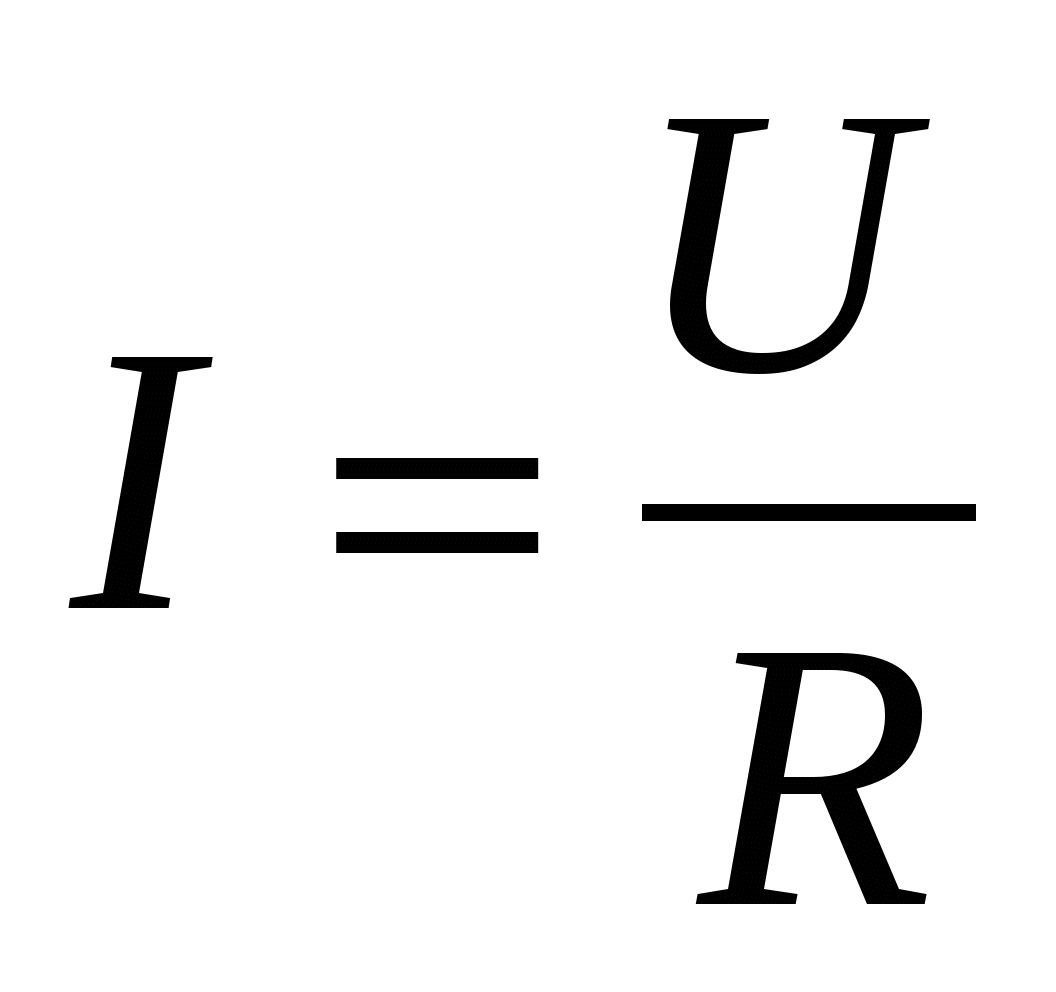 . . | (15.9) |
Vamos encontrar em (15.9) a tensão você e substitua em (15.8): RI= E +( 1 – 2 ) , (15.10)
A expressão resultante é a lei de Ohm para uma seção não uniforme da cadeia, ou seja, seção do circuito contendo EMF.

Arroz. 15.2
No uso pratico fórmula (15.10) você precisa definir os sinais de tensão e fem. Para fazer isso, definimos arbitrariamente a direção do desvio (na Fig. 15.2, a direção do desvio é escolhida no sentido horário). Se o sentido da corrente coincidir com o sentido do bypass, então é tomado com o sinal “+”, caso contrário deve ser tomado com o sinal “-”. Na Fig. 15.2 a direção do bypass e a direção da corrente não coincidem, portanto na fórmula (15.10) RI considere-o com um sinal de menos.
O resto do circuito fechado da Fig. 15.2 é mostrado com uma linha pontilhada. EMF por circuito externo“dispersa” cargas do seu “mais” para o seu “menos”. Deve ser tomada com sinal “+” se atuar no sentido de bypass e com sinal “–” caso contrário. De acordo com isso, no diagrama mostrado na Fig. 15.2, o EMF deve ser tomado com o sinal “+”. Assim, neste caso escrevemos a lei de Ohm para uma seção não uniforme da cadeia na forma: –
RI=
E
+(
1
–
2
)
.
^
15.3.2. Lei de Ohm para um circuito completo
Ao caminhar por aí cadeia completa os pontos inicial e final são iguais, então 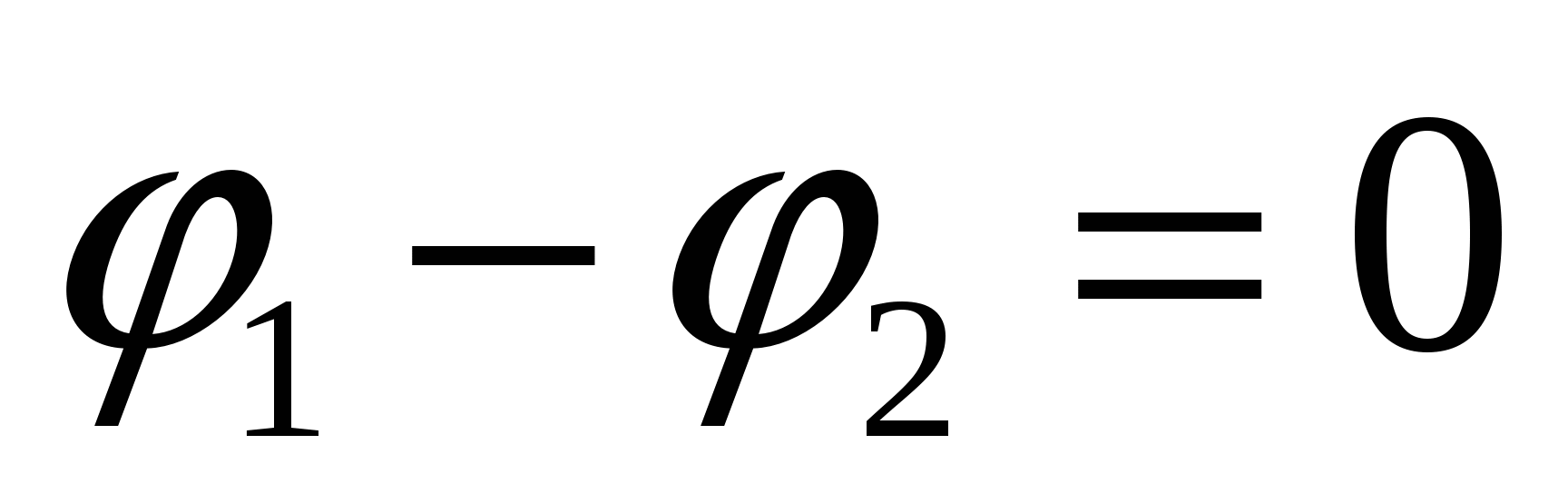 ;
;
^
15.3.3. Lei de Ohm para uma seção homogênea de uma cadeia
Uma seção do circuito que não contém uma fonte EMF é chamada de homogênea, ou seja, na fórmula (15.10) precisamos colocar E
=0
. Então 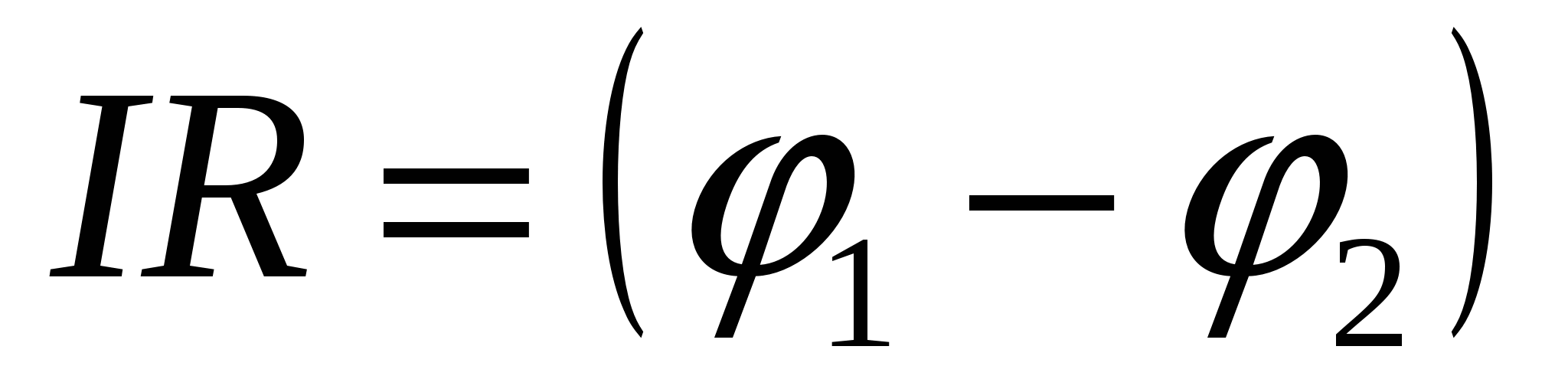 .
.
Neste caso, a queda de tensão coincide com a diferença de potencial você= 1 - 1, ou seja,
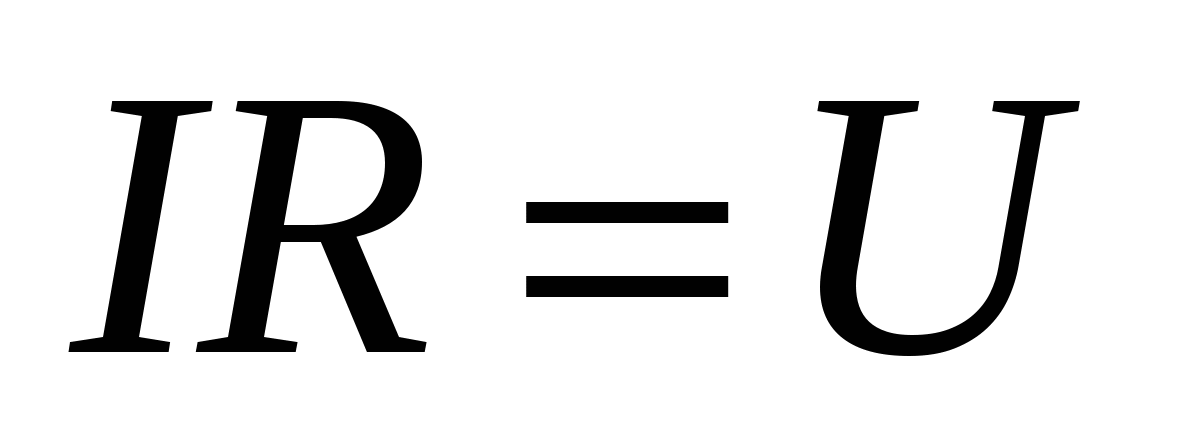 , , | (15.13) |
que também coincide com (15.9).
As fórmulas (15.9) e (15.13) representam a lei de Ohm na forma integral.
^
15.3.4. Lei de Ohm na forma diferencial
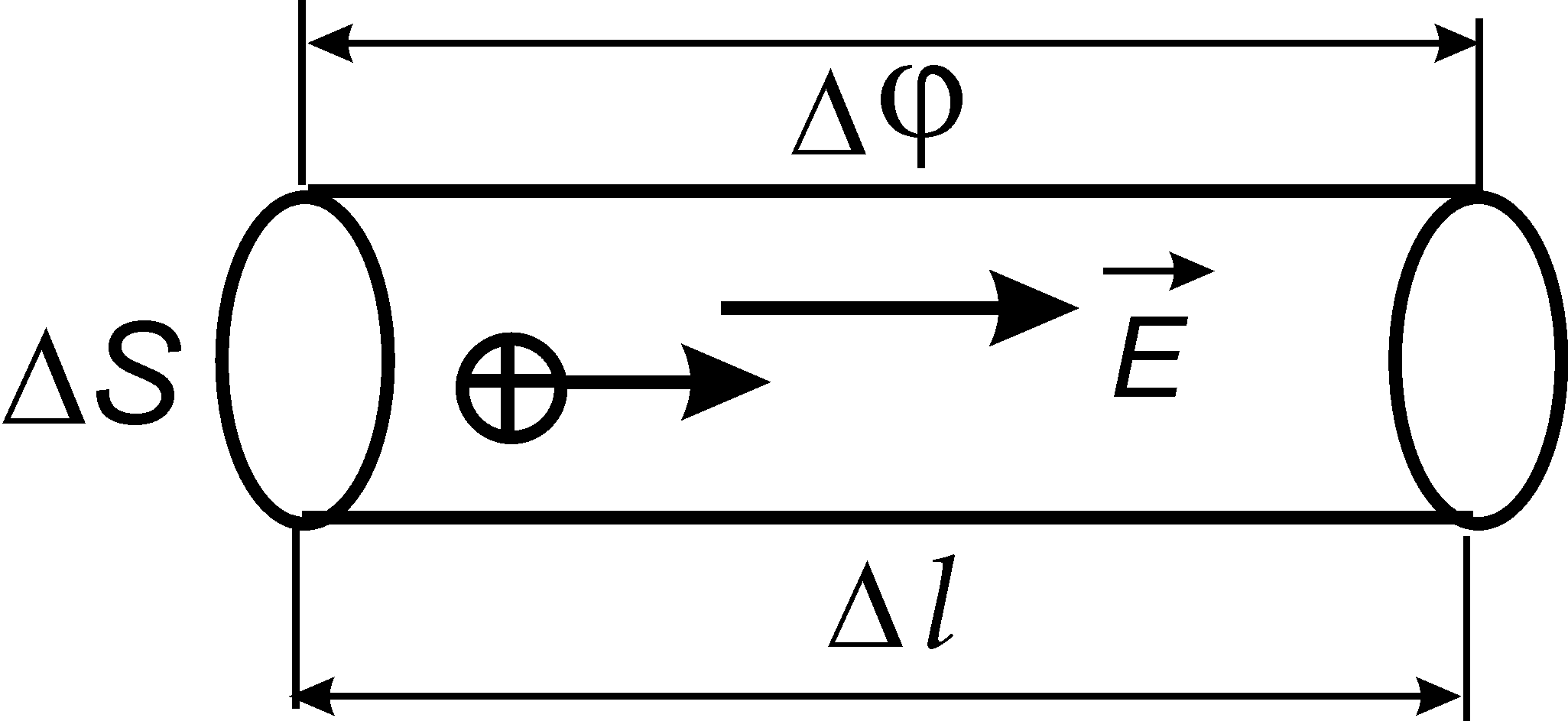
Arroz. 5.3
Vamos selecionar um cilindro elementar com seção transversal dentro do condutor condutor de corrente S e comprimento eu(Fig. 15.3). A força atual nele EU=S, e sua resistência  , onde é a resistividade do condutor. Diferença de potencial nas extremidades do cilindro . Então escrevemos a lei de Ohm (ver (15.9)) na forma
, onde é a resistividade do condutor. Diferença de potencial nas extremidades do cilindro . Então escrevemos a lei de Ohm (ver (15.9)) na forma
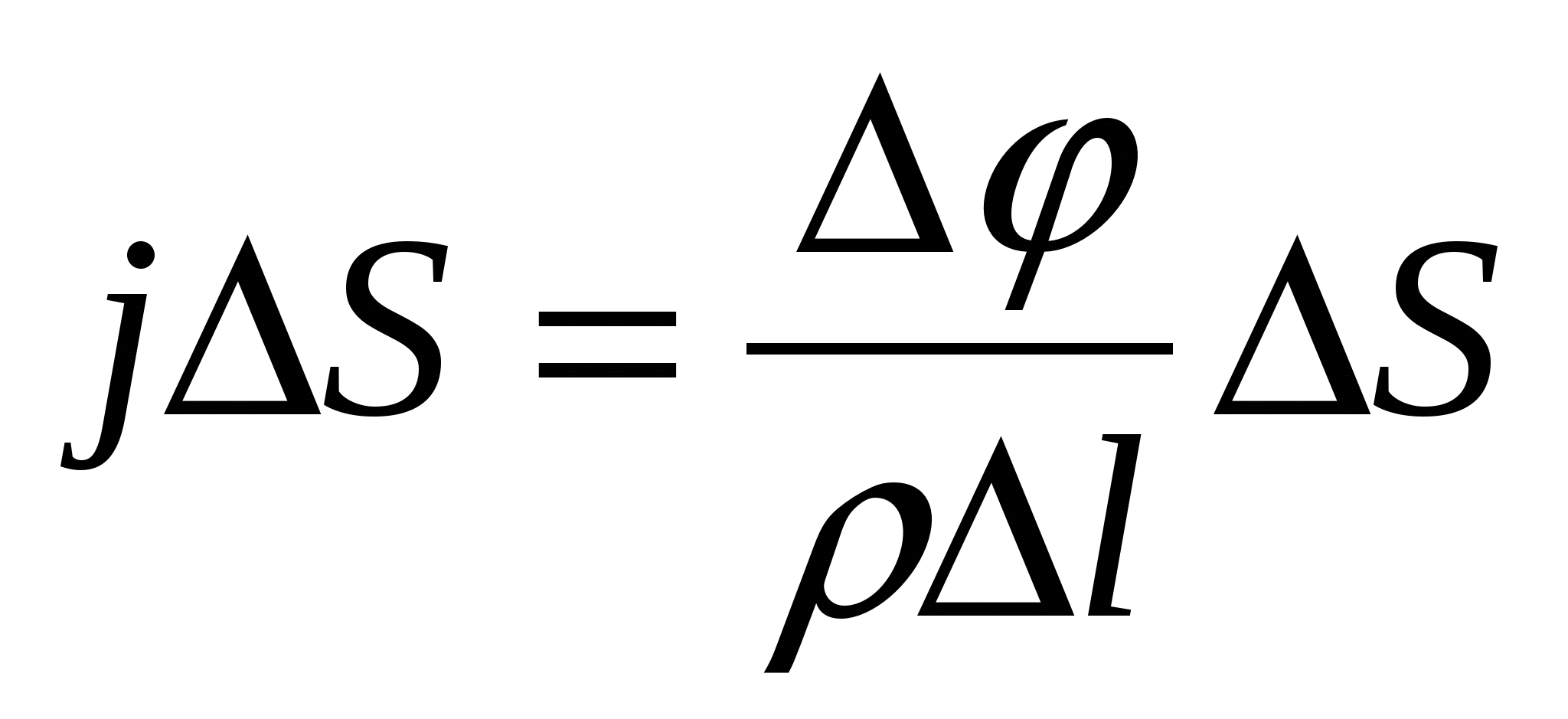 ou .
ou .
Levando em consideração (11.30), a última expressão pode ser transformada na forma
 . . | (15.14) |
O recíproco da resistividade é chamado de condutividade:
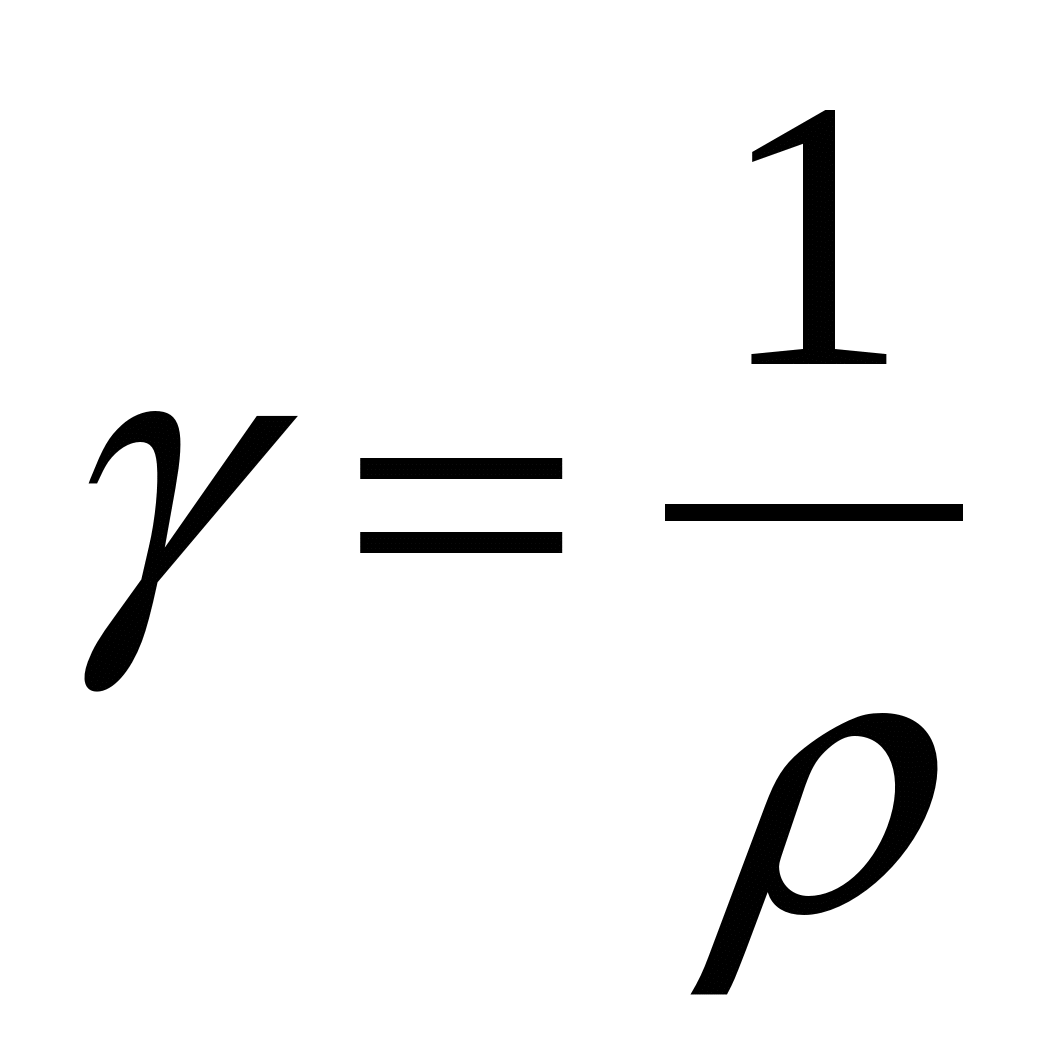 .
.Então a lei de Ohm na forma diferencial (15.4) pode ter a forma 
^
15.4. Lei de Joule-Lenz
15.4.1. Lei de Joule-Lenz na forma integral
Joule e, independentemente dele, Lenz estabeleceram experimentalmente cem a quantidade de calor liberada em um condutor por resistência R durante dt, proporcional ao quadrado da corrente, resistência e tempo: 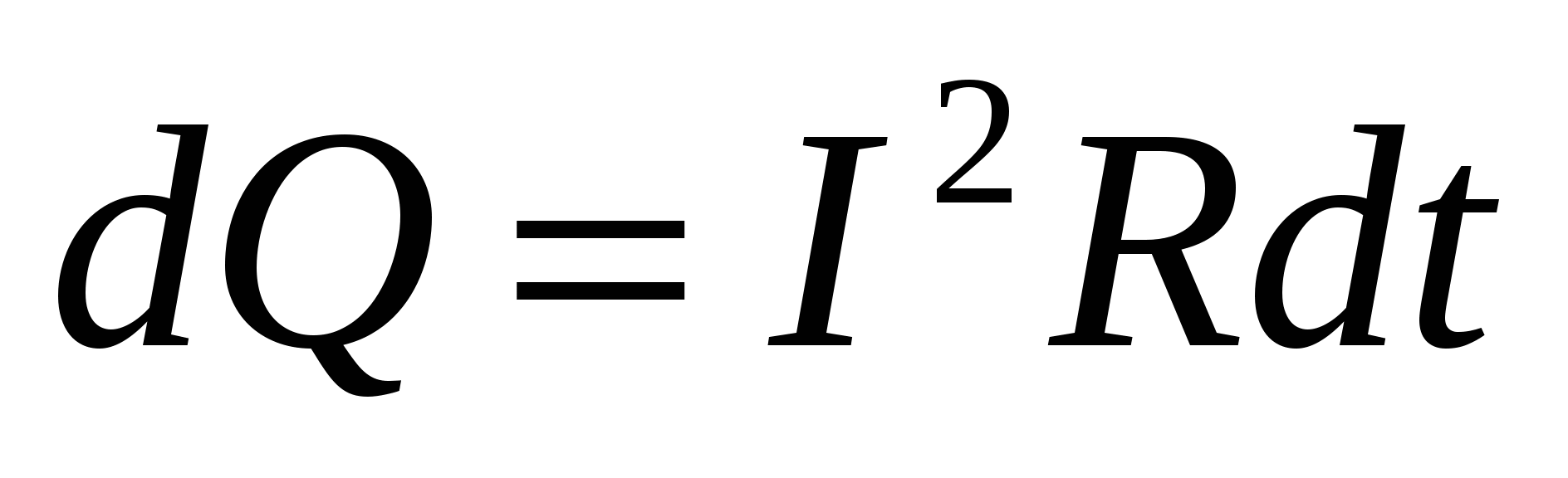 . . | (15.16) |
A fórmula (15.16) representa a lei de Joule-Lenz na forma integral.
^
15.4.2. Lei de Joule-Lenz em forma diferencial
Selecionemos, como antes, um volume cilíndrico elementar dentro do condutor (Fig. 15.3). Vamos substituir em (15.16)
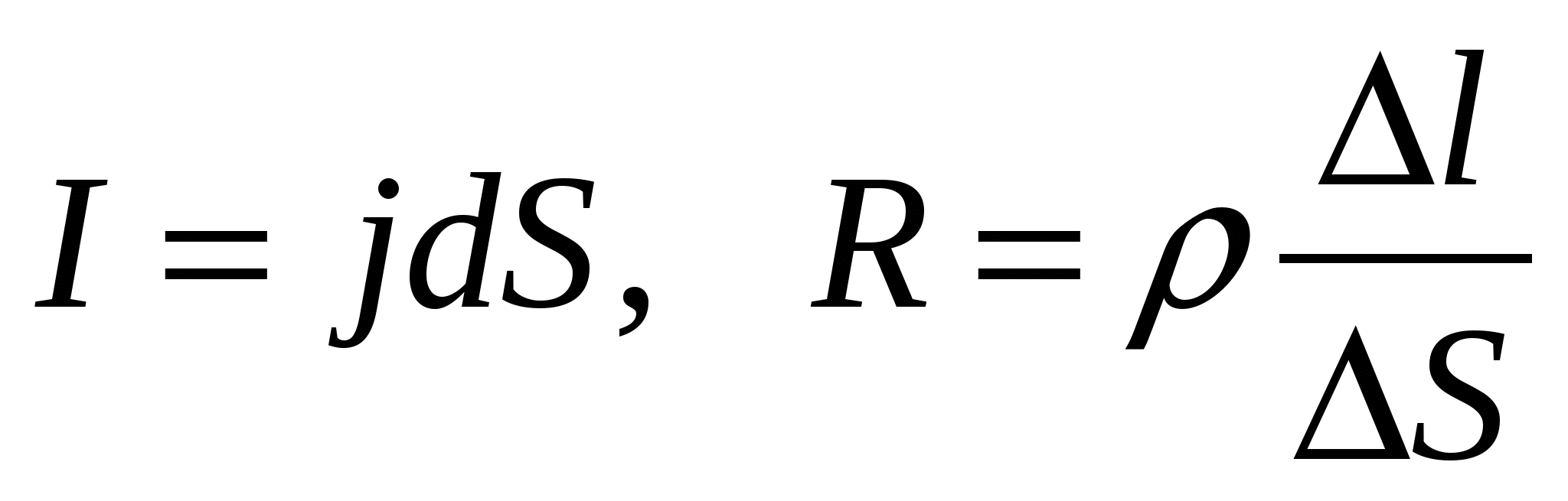 . Então
. Então  Onde V= euS– volume do condutor. Vamos apresentar a potência térmica específica
Onde V= euS– volume do condutor. Vamos apresentar a potência térmica específica 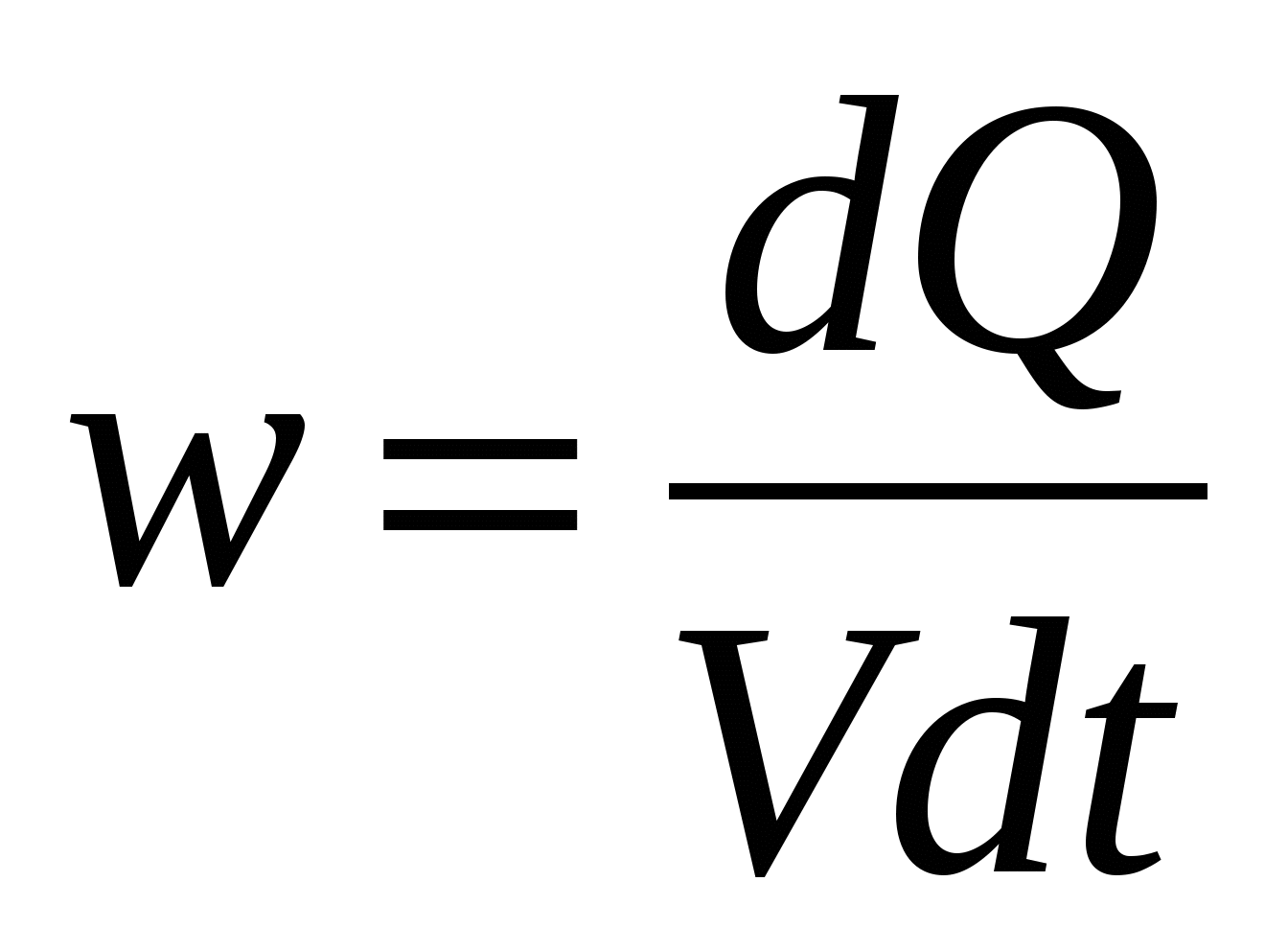 [J/m 3 s = W/m 3 ]. [J/m 3 s = W/m 3 ]. | (15.18) |
A potência térmica específica é numericamente igual à quantidade de calor liberada por unidade de volume do condutor por unidade de tempo. Em outras palavras, esta é a potência térmica desenvolvida por unidade de volume. Levando em consideração (15.18), a expressão (15.17) pode receber a forma
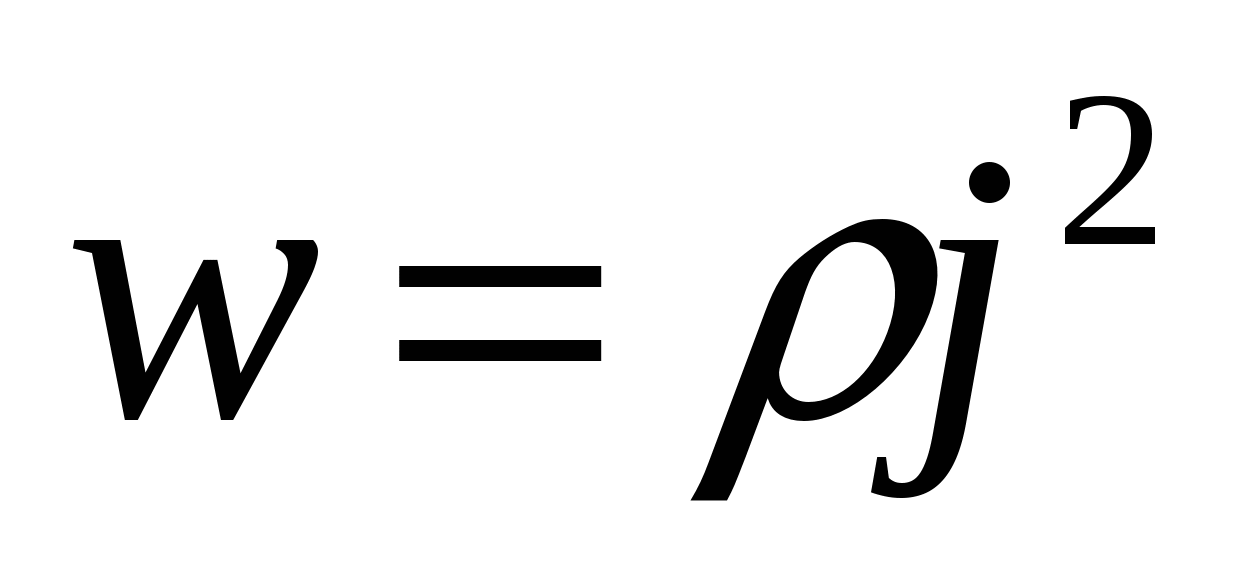 .
.
As fórmulas (15.19) e (15.20) representam a lei de Joule-Lenz na forma diferencial.
Aula 24.
^
15.5. Justificativa das leis de Ohm e Joule-Lenz de acordo com a teoria eletrônica clássica
Em clássico teoria do elétron metais o seguinte modelo é aceito.
1. Os portadores de corrente nos metais são elétrons livres.
2. Os elétrons livres formam um gás de elétrons, que tem propriedades semelhantes a um gás ideal. Há apenas uma diferença: quando os elétrons se movem, eles não colidem entre si, mas com os íons da rede cristalina.
3. Sob a influência de um campo elétrico, os elétrons, juntamente com um movimento caótico com velocidade  começar a se mover em uma direção em velocidade
começar a se mover em uma direção em velocidade  . Neste caso, a velocidade do movimento direcionado é significativamente menor que a velocidade do movimento caótico
. Neste caso, a velocidade do movimento direcionado é significativamente menor que a velocidade do movimento caótico
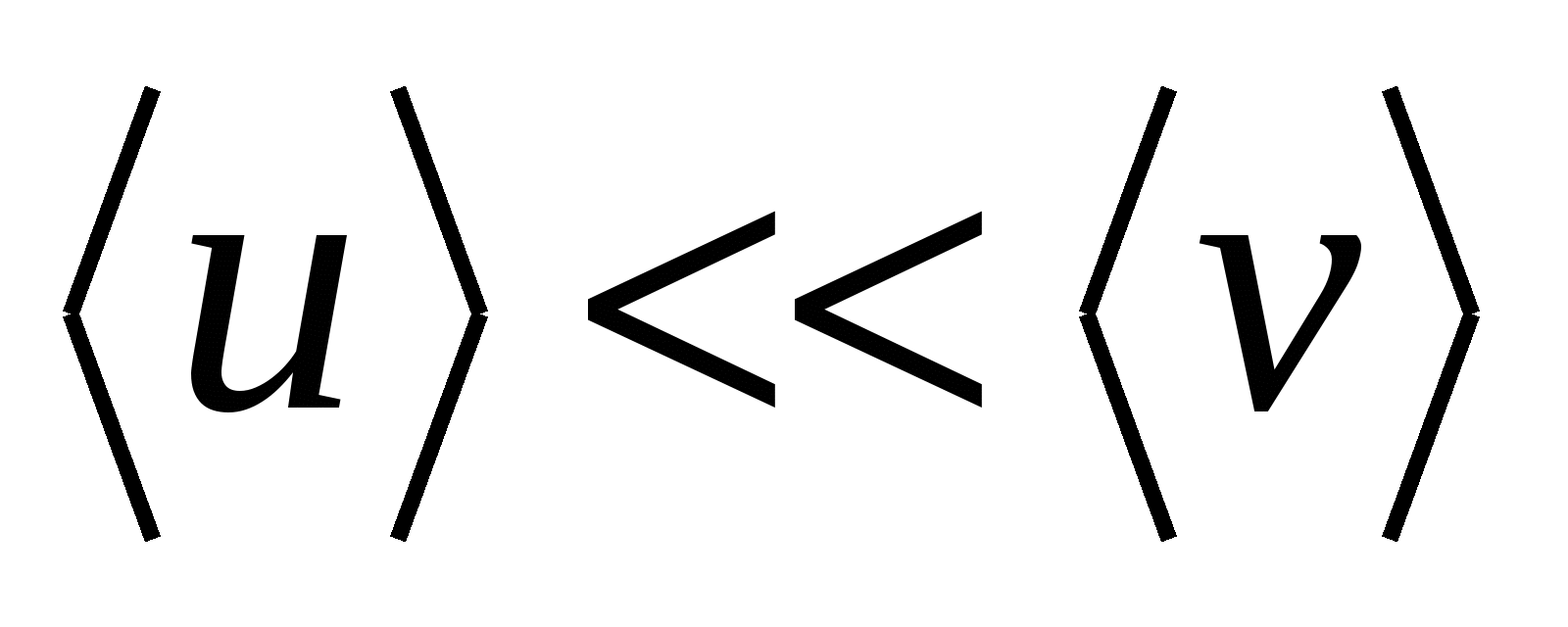 . . | (15.21) |
Vamos encontrar a velocidade do movimento direcional dos elétrons. Suponhamos que no momento t= 0 velocidade de movimento direcional dos elétrons você 0 =0. Sob força F=eE o elétron, de acordo com a segunda lei de Newton, começa a se mover acelerado:
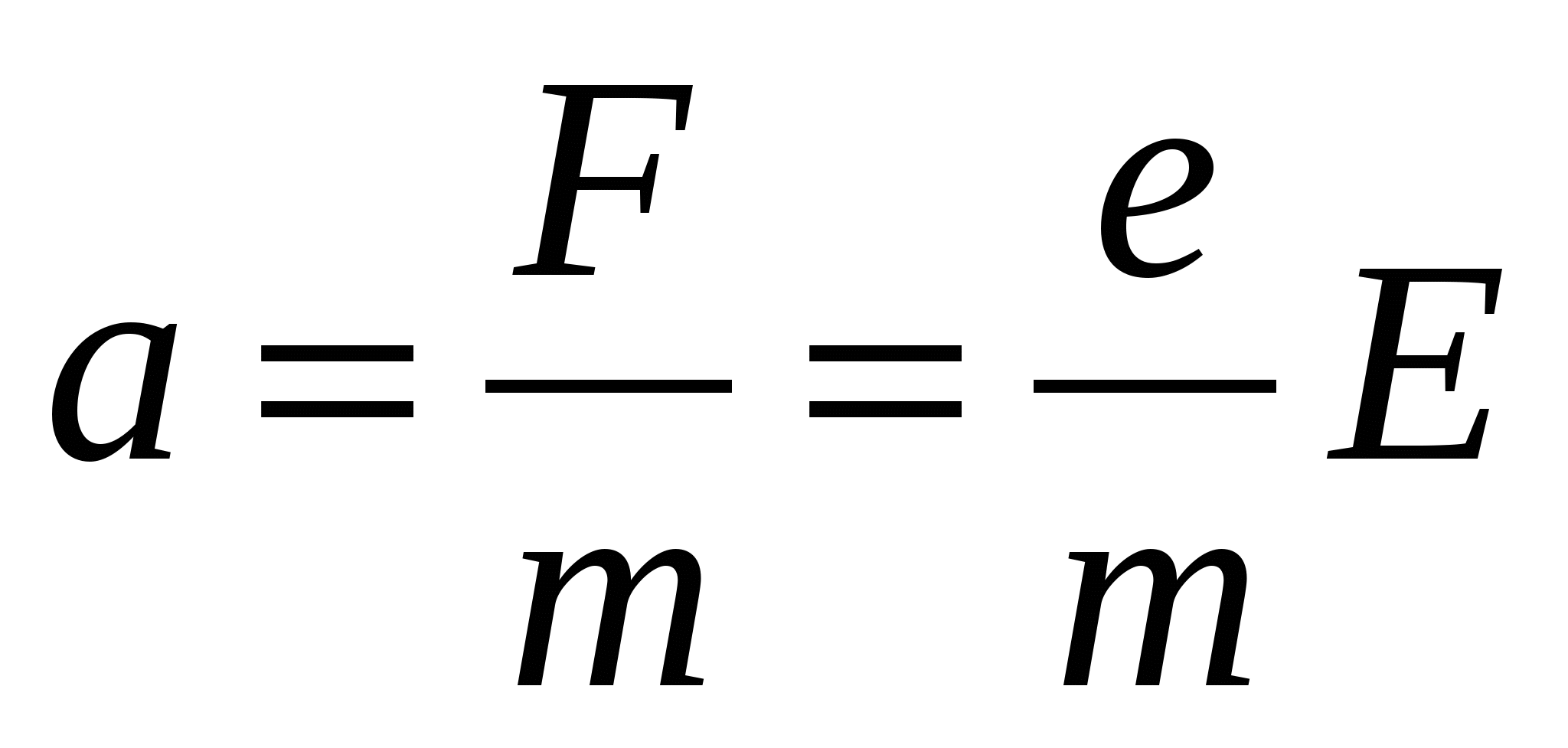 .
.
Velocidade do movimento direcional do elétron
 . . | (15.22) |

Arroz. 15.4
Da fórmula (15.22) segue-se que a velocidade do elétron você deve aumentar indefinidamente ao longo do tempo. No entanto, após um certo período de tempo o elétron experimenta uma colisão com um íon da rede cristalina e para. A dependência da velocidade do movimento direcional com o tempo é mostrada esquematicamente na Fig. 15.4.
Tempo médio entre duas colisões de elétrons sucessivas
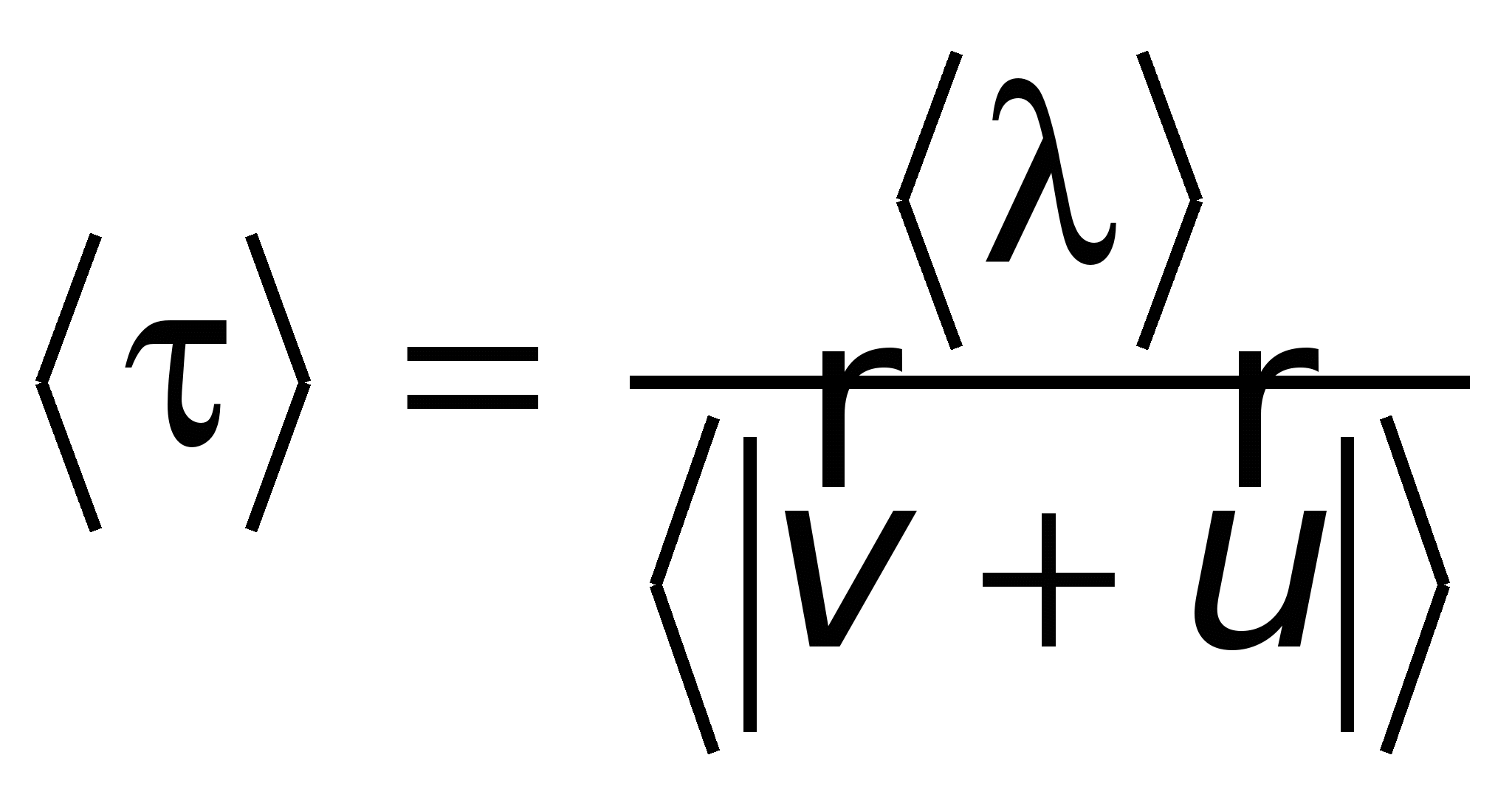 , , | (15.23) |
Onde
 – caminho livre médio de um elétron;
– caminho livre médio de um elétron;  – o valor médio de sua velocidade, que é a soma vetorial das velocidades dos movimentos caóticos e direcionais.
– o valor médio de sua velocidade, que é a soma vetorial das velocidades dos movimentos caóticos e direcionais. Devido à desigualdade (15.21), a velocidade do movimento direcionado pode ser desprezada, portanto
 . .
através das características do gás de elétrons. Com base nos conceitos da teoria eletrônica clássica dos metais, obtemos agora a lei de Joule-Lenz. Ao final do caminho livre, o elétron possui energia cinética de movimento direcionado
Substituindo aqui o valor da velocidade máxima do movimento direcional do elétron de (15.25) e levando em consideração que o número médio de colisões em 1 s
obtemos a lei de Joule-Lenz
A partir de uma comparação de (15.30) e (15.20) encontramos a mesma expressão para condutividade térmica, como na lei de Ohm (ver (15.28)). Apesar dos sucessos óbvios da teoria eletrônica clássica dos metais, ela encontrou uma série de dificuldades. Em particular, a teoria clássica prevê incorretamente a dependência da resistência do metal com a temperatura. A análise da expressão (15.29) mostra que apenas a velocidade do movimento caótico depende da temperatura. Neste caso (ver fórmula (8.18)) Arroz. 15,5 A primeira regra de Kirchhoff. A soma algébrica das correntes convergindo em um nó é igual a zero, ou seja,
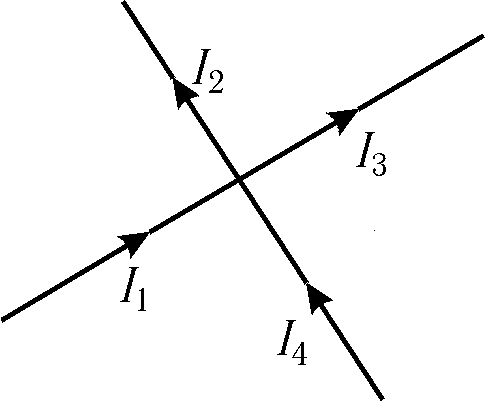
Um nó é um ponto em um circuito onde três ou mais condutores se cruzam. A corrente é tomada com sinal “+” se entrar no nó; a corrente que sai do nó é obtida com um sinal “-”. Arroz. 15.6 aqueles. a soma das correntes que entram em um nó é igual à soma das correntes que saem dele. A primeira regra de Kirchhoff é uma consequência da lei da conservação da carga elétrica: as cargas, uma vez em um nó, não desaparecem nem se acumulam em lugar nenhum. ^
A segunda regra de Kirchhoff.
A soma algébrica das quedas de tensão em um circuito fechado isolado de um circuito complexo é igual à soma algébrica das fem incluídas neste circuito:
A queda de tensão é medida com sinal “+” se a corrente for direcionada para contornar o circuito, e “-” caso contrário. O EMF é obtido com sinal “+” se atuar na direção de bypass e “-” caso contrário. A direção do desvio é escolhida arbitrariamente. Para maior definição, escolhemos a direção do percurso no sentido horário. Vamos escrever, por exemplo, a segunda regra de Kirchhoff para contornos ^ ABCFA E ABCDEFA(Fig. 15.7): o circuito ABCFA: EU 1 R 1 +EU 2 R 2 = E 1 – E 2 ; Circuito ABCDEFA: EU 1 R 1 -EU 3 R 3 = E 1 – E 3 . No caso geral, quando o circuito tem n nós e eu contornos, você precisa fazer n-1 equação de acordo com a primeira regra de Kirchhoff e eu-1 equação de acordo com a segunda regra. 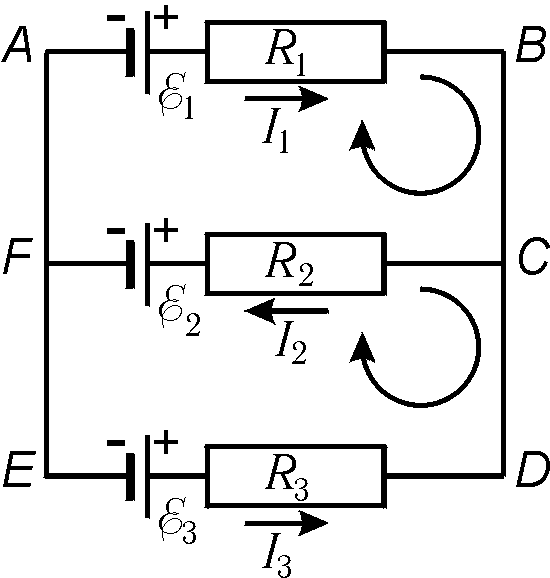 Arroz. 15,7 Aula 25. |
1. Energia de um sistema de cargas pontuais estacionárias. As forças de interação eletrostática são conservadoras; portanto, o sistema de cargas tem energia potencial. Vamos encontrar a energia potencial de um sistema de duas cargas pontuais estacionárias e localizadas a uma distância r uma da outra. Cada uma dessas cargas no campo da outra tem energia potencial:
, ![]() ,
,
onde e são, respectivamente, os potenciais criados pela carga no ponto onde a carga está localizada e pela carga no ponto onde a carga está localizada. De acordo com a fórmula (8.3.6),
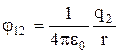 E
E 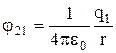 ,
,
![]()
Ao adicionar cargas , ,… a um sistema de duas cargas sucessivas, pode-se verificar que no caso de n cargas estacionárias, a energia de interação do sistema de cargas pontuais é igual a
 , (8.12.1.)
, (8.12.1.)
onde é o potencial criado no ponto onde a carga está localizada por todas as cargas, exceto a i-ésima.
2. Energia de um condutor solitário carregado. Seja um condutor solitário cuja carga, capacitância e potencial sejam respectivamente iguais a q, C, . Vamos aumentar a carga deste condutor em dq. Para isso, é necessário transferir a carga dq do infinito para um condutor isolado, gastando um trabalho igual a
![]() .
.
Para carregar um corpo do potencial zero até , é necessário realizar trabalho
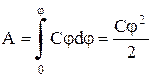 . (8.12.2.)
. (8.12.2.)
A energia de um condutor carregado é igual ao trabalho que deve ser realizado para carregar este condutor:
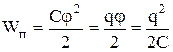 . (8.12.3.)
. (8.12.3.)
A fórmula (8.12.3.) também pode ser obtida pelo fato de que o potencial do condutor em todos os seus pontos é o mesmo, uma vez que a superfície do condutor é equipotencial. Assumindo o potencial do condutor igual a, de (8.12.1.) encontramos
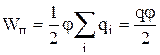 ,
,
onde está a carga do condutor.
3. Energia de um capacitor carregado. Como qualquer condutor carregado, um capacitor possui energia que, de acordo com a fórmula (8.12.3.), é igual a
 , (8.12.4.)
, (8.12.4.)
onde q é a carga do capacitor, C é sua capacidade e é a diferença de potencial entre as placas.
4. Energia do campo eletrostático. Vamos transformar a fórmula (8.12.4.), que expressa a energia de um capacitor plano em termos de cargas e potenciais, utilizando a expressão para a capacitância de um capacitor plano e a diferença de potencial entre suas placas (). Então obtemos
 , (8.12.5.)
, (8.12.5.)
onde V = Sd é o volume do capacitor. A fórmula (8.12.5.) mostra que a energia do capacitor é expressa através de uma quantidade que caracteriza o campo eletrostático - tensão E.
As fórmulas (8.12.4.) e (8.12.5.) relacionam respectivamente a energia do capacitor com carga em suas capas e com força de campo. Naturalmente, surge a questão da localização energia eletrostática e qual é a sua operadora - cargas ou campo? A resposta a esta pergunta só pode ser dada pela experiência. A eletrostática estuda campos constantes no tempo de cargas estacionárias, ou seja, nele os campos e as cargas que os determinam são inseparáveis entre si. Portanto, a eletrostática não pode responder às questões colocadas. O desenvolvimento adicional da teoria e do experimento mostrou que Campos magnéticos podem existir separadamente, independentemente das cargas que os excitaram, e se espalhar no espaço na forma ondas eletromagnéticas, capaz transferir energia. Isto confirma de forma convincente o ponto principal teoria de curto alcance de localização de energia em um campo E daí operadora energia é campo.
Densidade aparente energia do campo eletrostático (energia por unidade de volume)
 . (8.12.6.)
. (8.12.6.)
A expressão (8.12.6.) é válida apenas para dielétrico isotrópico, para o qual vale a seguinte relação: .
A energia elétrica de um capacitor de placas paralelas pode ser expressa em termos da intensidade do campo entre suas placas:
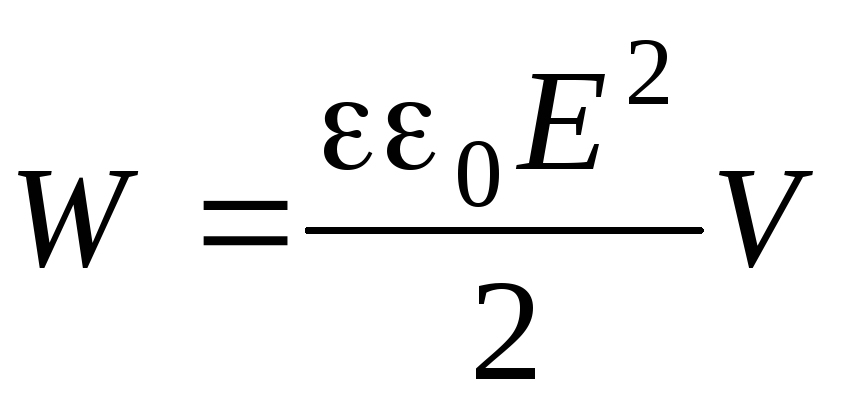 ,
,
Onde - volume de espaço ocupado pelo campo, S– área dos revestimentos, d– a distância entre eles. Acontece que a tensão pode ser expressa energia elétrica e um sistema arbitrário de condutores carregados e dielétricos:
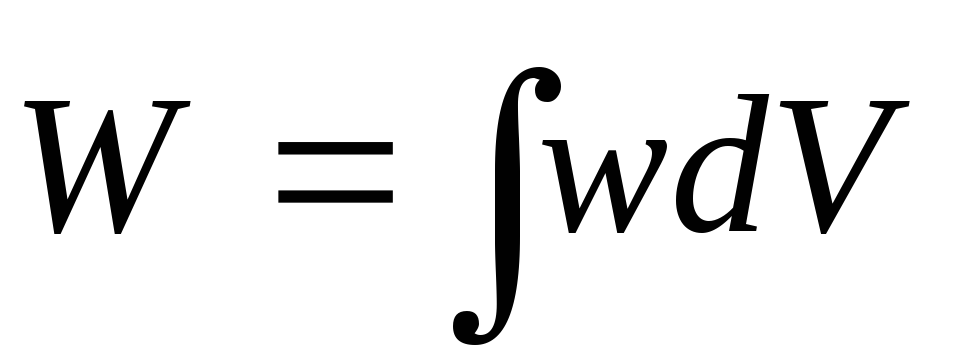 ,
(5)
,
(5)
 ,
,
e a integração é realizada em todo o espaço ocupado pelo campo (presume-se que o dielétrico é isotrópico e 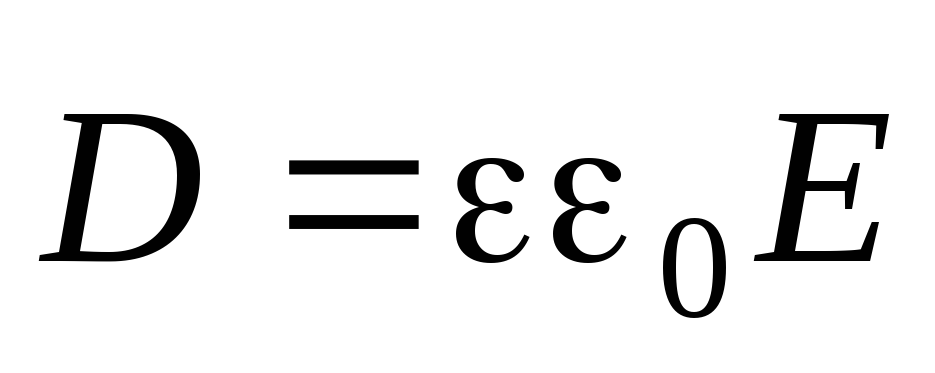 ). Magnitude c representa energia elétrica por unidade de volume. A forma da fórmula (5) dá motivos para supor que a energia elétrica está contida não em cargas em interação, mas em seu campo elétrico preenchendo o espaço. No âmbito da eletrostática, esta suposição não pode ser verificada experimentalmente ou fundamentada teoricamente, mas a consideração de campos elétricos e magnéticos alternados permite verificar a exatidão da interpretação deste campo da fórmula (5).
). Magnitude c representa energia elétrica por unidade de volume. A forma da fórmula (5) dá motivos para supor que a energia elétrica está contida não em cargas em interação, mas em seu campo elétrico preenchendo o espaço. No âmbito da eletrostática, esta suposição não pode ser verificada experimentalmente ou fundamentada teoricamente, mas a consideração de campos elétricos e magnéticos alternados permite verificar a exatidão da interpretação deste campo da fórmula (5).
7. Energia do campo elétrico (exemplos de resolução de problemas) Energia de interação de carga
Exemplo 1.
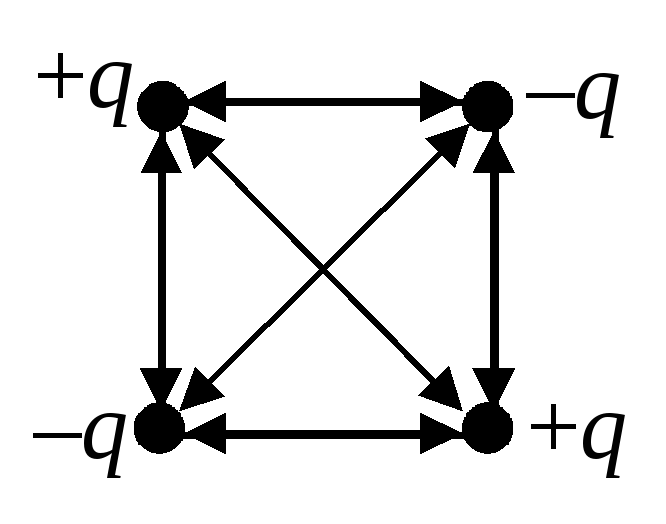
Determine a energia elétrica de interação de cargas pontuais localizadas nos vértices de um quadrado com lado a(ver Fig. 2).
Solução.
Na Fig. 3, todas as interações de cargas em pares são convencionalmente representadas por setas de duas direções. Levando em conta as energias de todas essas interações, obtemos:
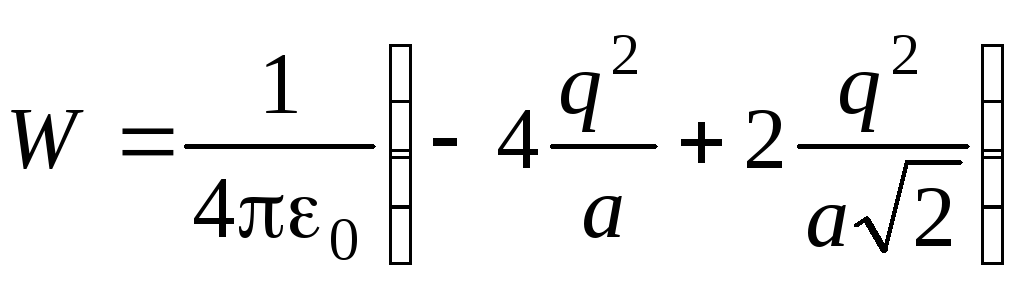 .
.
|
|
|
|
Exemplo 2.
Determine a energia elétrica de interação de um anel carregado com um dipolo localizado em seu eixo, conforme mostrado na Fig. Distâncias conhecidas a, eu, cobranças P, q e raio do anel R.
Solução.
Ao resolver o problema, deve-se levar em consideração todas as energias das interações dos pares de cargas de um corpo (anel) com cargas de outro corpo (dipolo). Energia de interação de uma carga pontual q com carga P distribuído ao longo do anel é determinado pela soma
![]() ,
,
Onde 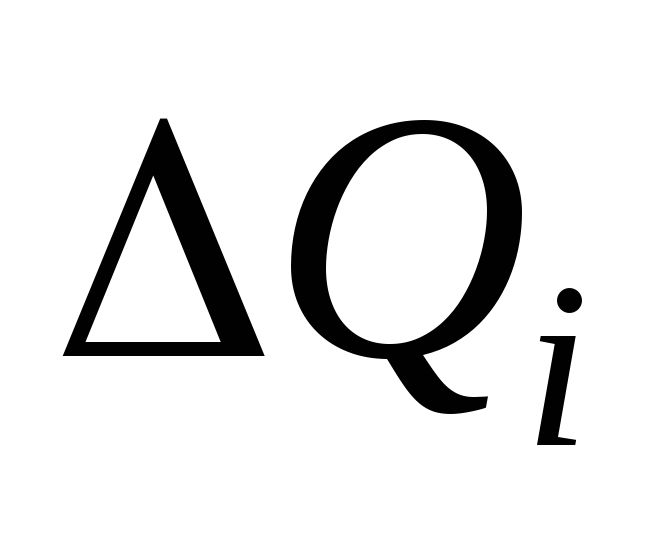 - carga de um fragmento de anel infinitesimal,
- carga de um fragmento de anel infinitesimal,
 -
distância deste fragmento até a carga q. Porque tudo
-
distância deste fragmento até a carga q. Porque tudo  iguais e iguais
iguais e iguais 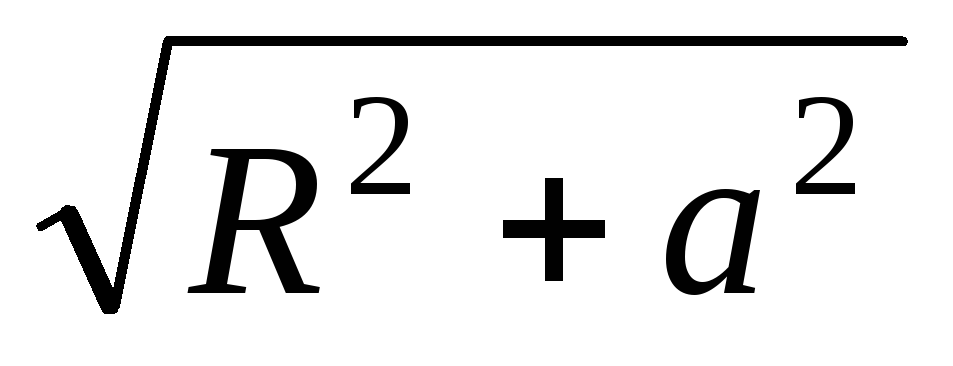 , Que
, Que
Da mesma forma, encontramos a energia de interação de uma carga pontual – q com anel carregado:
Resumindo C 1 e C 2, obtemos para a energia de interação do anel com o dipolo:
 .
.
Energia elétrica de condutores carregados
Exemplo 3.
Defina o trabalho forças elétricas quando o raio de uma esfera uniformemente carregada diminui por um fator de 2. Carga de esfera q, seu raio inicial R.
Solução.
A energia elétrica de um condutor solitário é determinada pela fórmula 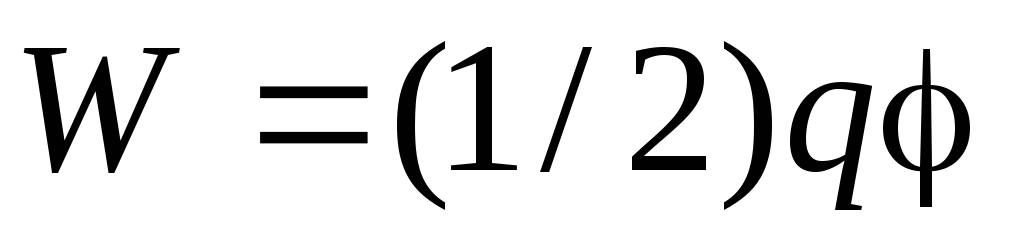 , Onde q– carga do condutor, – seu potencial. Considerando que o potencial de uma esfera uniformemente carregada de raio Ré igual a
, Onde q– carga do condutor, – seu potencial. Considerando que o potencial de uma esfera uniformemente carregada de raio Ré igual a  , vamos encontrar sua energia elétrica:
, vamos encontrar sua energia elétrica:
 .
.
Depois que o raio da esfera é reduzido à metade, sua energia se torna igual a
 .
.
As forças elétricas funcionam
 .
.
Exemplo 4.
Duas esferas metálicas cujos raios são R e 2 R, e as cobranças correspondentes são 2 q E - q, localizados no vácuo a uma grande distância um do outro. Quantas vezes a energia elétrica do sistema diminuirá se as bolas estiverem conectadas com um fio fino?
Solução.
Depois de conectar as bolas com um fio fino, seus potenciais tornam-se os mesmos
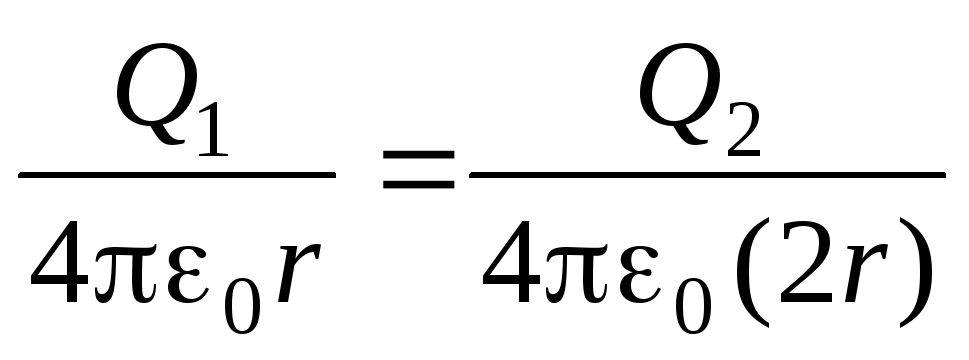 ,
,
e as cargas constantes das bolas P 1 e P 2 são obtidos como resultado do fluxo de carga de uma bola para outra. Neste caso, a carga total das bolas permanece constante:
 .
.
A partir dessas equações encontramos
 ,
, .
.
A energia das bolas antes de serem conectadas por fio é igual a
 ,
,
e depois da conexão
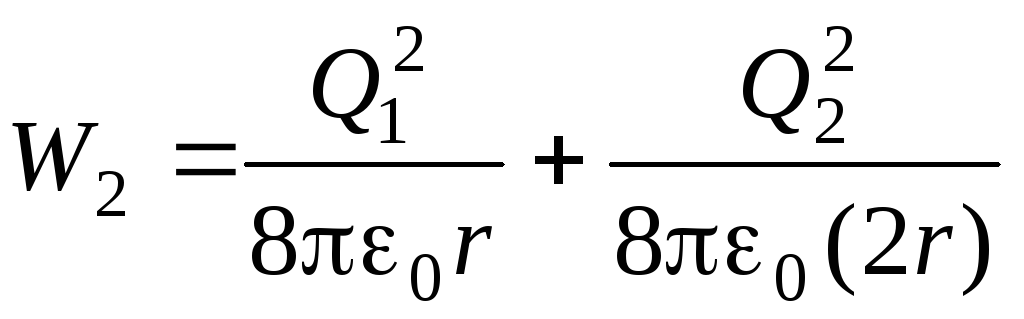 .
.
Substituindo valores na última expressão P 1 e P 2, obtemos após transformações simples
 .
.
Exemplo 5.
Fundido em uma bola N= 8 bolas idênticas de mercúrio, cada uma com carga q. Considerando que no estado inicial as bolas de mercúrio estavam ligadas longa distância um do outro, determine quantas vezes a energia elétrica do sistema aumentou.
Solução.
Quando as esferas de mercúrio se fundem, sua carga e volume totais são preservados:
![]() ,
,
Onde P– carga da bola, R– seu raio, Ré o raio de cada pequena bola de mercúrio. Energia elétrica total N bolas solitárias é igual a
 .
.
Energia elétrica da bola resultante
 .
.
Depois das transformações algébricas obtemos
 = 4.
= 4.
Exemplo 6.
Bola de raio de metal R= 1 mm e carga q= 0,1nC de uma grande distância eles se aproximam lentamente de um condutor descarregado e param quando o potencial da bola se torna igual a = 450 V. Que trabalho deve ser feito para isso?
Solução.
A energia elétrica de um sistema de dois condutores carregados é determinada pela fórmula
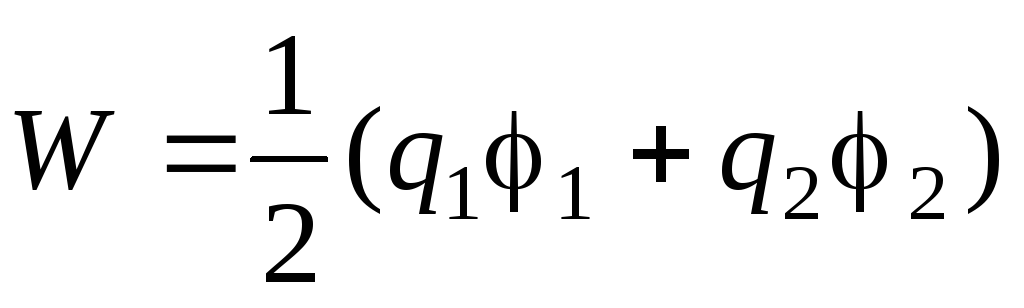 ,
,
Onde q 1 e q 2 – cargas dos condutores, 1 e 2 – seus potenciais. Como o condutor de acordo com o problema não está carregado, então
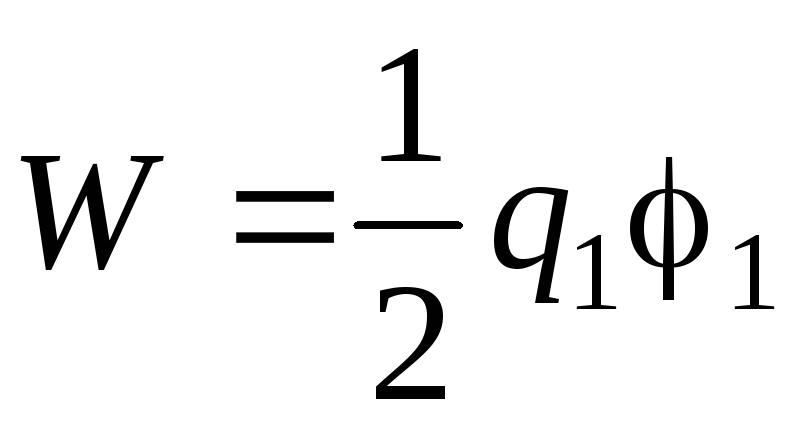 ,
,
Onde q 1 e 1 carga e potencial da bola. Quando a bola e o condutor descarregado estão a uma grande distância um do outro,
 ,
,
e energia elétrica do sistema
 .
.
No estado final do sistema, quando o potencial da bola se torna igual a , a energia elétrica do sistema é:
 .
.
O trabalho das forças externas é igual ao incremento da energia elétrica:
 = –0,0225 µJ.
= –0,0225 µJ.
notar que campo elétrico no estado final do sistema é criado por cargas induzidas no condutor, bem como por cargas distribuídas de maneira não uniforme sobre a superfície da bola metálica. É muito difícil calcular este campo com uma geometria de condutor conhecida e uma determinada posição da bola metálica. Não foi necessário fazer isso, pois o problema não especifica a configuração geométrica do sistema, mas sim o potencial da bola no estado final.
Exemplo 7 .
O sistema consiste em duas cascas metálicas finas concêntricas com raios R 1 e R 2
( e encargos correspondentes q 1 e q 2. Encontre energia elétrica C sistemas. Considere também o caso especial quando
e encargos correspondentes q 1 e q 2. Encontre energia elétrica C sistemas. Considere também o caso especial quando ![]() .
.
Solução.
A energia elétrica de um sistema de dois condutores carregados é determinada pela fórmula
 .
.
Para resolver o problema, é necessário encontrar os potenciais das esferas interna ( 1) e externa ( 2). Isto não é difícil de fazer (veja a seção correspondente do manual):
 ,
, .
.
Substituindo essas expressões na fórmula da energia, obtemos
 .
.
No ![]() energia é igual
energia é igual
 .
.
Pergunta nº 1
Campo elétrico. Para explicar a natureza das interações elétricas dos corpos carregados, é necessário assumir a presença no espaço circundante das cargas de um agente físico que realiza essa interação. Conforme teoria de curto alcance, que afirma que as interações de força entre os corpos são realizadas através de um ambiente material especial que envolve os corpos em interação e transmite quaisquer mudanças em tais interações no espaço com uma velocidade finita, tal agente é campo elétrico.
O campo elétrico é criado por cargas estacionárias e móveis. A presença de um campo elétrico pode ser avaliada, em primeiro lugar, pela sua capacidade de exercer um efeito de força sobre cargas eletricas, móveis e estacionários, bem como pela capacidade de induzir cargas elétricas na superfície de corpos neutros condutores.
O campo criado por cargas elétricas estacionárias é chamado elétrico estacionário, ou eletrostático campo. Representa caso especial campo eletromagnetico, através do qual são realizadas interações de força entre corpos eletricamente carregados, movendo-se no caso geral de maneira arbitrária em relação ao sistema de referência.
Intensidade do campo elétrico. Uma característica quantitativa da ação da força de um campo elétrico sobre corpos carregados é a grandeza vetorial E, chamado intensidade do campo elétrico.
E= F / q etc.
É determinado pela razão de força F, agindo a partir do campo em uma carga de teste pontual q pr, colocado no ponto de campo em consideração, à magnitude desta carga.
O conceito de “carga de teste” pressupõe que esta carga não participa da criação do campo elétrico e é tão pequena que não o distorce, ou seja, não provoca uma redistribuição no espaço das cargas que criam o campo em questão. A unidade SI de tensão é 1 V/m, o que equivale a 1 N/C.
Intensidade de campo de uma carga pontual. Usando a lei de Coulomb, encontramos uma expressão para a intensidade do campo elétrico criado por uma carga pontual q em um meio isotrópico homogêneo à distância R da cobrança:
Nesta fórmula R– cargas de conexão do vetor raio q E q etc. De (1.2) segue-se que a tensão E campos de carga pontual q em todos os pontos do campo é direcionado radialmente a partir da carga em q> 0 e carregar em q< 0.
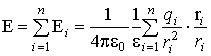 Princípio da superposição. Força de campo gerado pelo sistema cargas pontuais estacionárias q 1 , q 2 , q 3, ¼, qn, é igual à soma vetorial das intensidades do campo elétrico criado por cada uma dessas cargas separadamente:
Princípio da superposição. Força de campo gerado pelo sistema cargas pontuais estacionárias q 1 , q 2 , q 3, ¼, qn, é igual à soma vetorial das intensidades do campo elétrico criado por cada uma dessas cargas separadamente:
, Onde eu– distância entre carga qi e o ponto de campo considerado.
Princípio da superposição, permite calcular não apenas a intensidade do campo de um sistema de cargas pontuais, mas também a intensidade do campo em sistemas onde há uma distribuição contínua de carga. A carga de um corpo pode ser representada como a soma das cargas pontuais elementares d q.
Além disso, se a taxa for distribuída com densidade linear t, então d q=td eu; se a carga for distribuída com densidade superficial s, então d q=d eu e d q= rd eu, se a carga for distribuída com densidade aparente R.
Pergunta nº 2
Fluxo vetorial de indução elétrica. O fluxo do vetor de indução elétrica é determinado de forma semelhante ao fluxo do vetor de intensidade do campo elétrico
dF D = D d S
Existe alguma ambiguidade nas definições de fluxos devido ao fato de que para cada superfície podem ser especificadas duas normais de direções opostas. Para uma superfície fechada, a normal externa é considerada positiva.
Teorema de Gauss. Consideremos uma carga elétrica pontual positiva q localizada dentro de uma superfície fechada arbitrária S (Fig. 1.3). O fluxo do vetor de indução através do elemento de superfície dS é igual a ![]()
Componente dS D = dS cosa do elemento de superfície d S na direção do vetor de indução D consideramos-o como um elemento de uma superfície esférica de raio r, no centro da qual está localizada uma carga q.
Levando em consideração que dS D / r 2 é igual ao ângulo sólido elementar dw, no qual o elemento de superfície dS é visível do ponto onde a carga q está localizada, transformamos a expressão (1.4) na forma dF D = q dw /4p, de onde, após integração em todo o espaço ao redor da carga, ou seja, dentro do ângulo sólido de 0 a 4p, obtemos
O fluxo do vetor de indução elétrica através de uma superfície fechada de formato arbitrário é igual à carga contida nesta superfície.
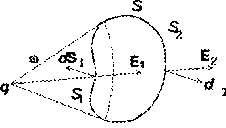
Se uma superfície fechada arbitrária S não cobre uma carga pontual q, então, construindo uma superfície cônica com o vértice no ponto onde a carga está localizada, dividimos a superfície S em duas partes: S 1 e S 2. Vetor de fluxo D através da superfície S encontramos como a soma algébrica dos fluxos através das superfícies S 1 e S 2:
![]() .
.
Ambas as superfícies do ponto onde a carga q está localizada são visíveis no mesmo ângulo sólido w. Portanto os fluxos são iguais
Como a normal externa à superfície é usada ao calcular o fluxo através de uma superfície fechada, é fácil ver que o fluxo Ф 1D< 0, тогда как поток Ф 2D >0. Fluxo total Ф D = 0. Isso significa que o fluxo do vetor de indução elétrica através de uma superfície fechada de formato arbitrário não depende das cargas localizadas fora desta superfície.
Se o campo elétrico é criado por um sistema de cargas pontuais q 1, q 2,¼, q n, que é coberto por uma superfície fechada S, então, de acordo com o princípio da superposição, o fluxo do vetor de indução através desta superfície é determinado como a soma dos fluxos criados por cada uma das cargas. O fluxo do vetor de indução elétrica através de uma superfície fechada de formato arbitrário é igual à soma algébrica das cargas cobertas por esta superfície:
Deve-se notar que as cargas q i não precisam ser pontuais, Condição necessaria- a área carregada deve estar completamente coberta pela superfície. Se no espaço delimitado por uma superfície fechada S a carga elétrica se distribui continuamente, então devemos assumir que cada volume elementar dV possui uma carga. Neste caso, no lado direito da expressão, a soma algébrica das cargas é substituída pela integração sobre o volume encerrado na superfície fechada S:
Esta expressão é a formulação mais geral do teorema de Gauss: o fluxo do vetor de indução elétrica através de uma superfície fechada de formato arbitrário é igual à carga total no volume coberto por esta superfície e não depende de cargas localizadas fora da superfície em questão ![]() .
.
Questão 3
Energia potencial de uma carga em um campo elétrico. Trabalho realizado pelas forças do campo elétrico ao mover uma carga pontual positiva q da posição 1 para a posição 2, imagine como uma mudança na energia potencial desta carga: ![]() , Onde C p1 e C p2 – energias potenciais de carga q nas posições 1 e 2. Com pequeno movimento de carga q no campo criado por uma carga pontual positiva P, a mudança na energia potencial é
, Onde C p1 e C p2 – energias potenciais de carga q nas posições 1 e 2. Com pequeno movimento de carga q no campo criado por uma carga pontual positiva P, a mudança na energia potencial é ![]() . No movimento de carga final q da posição 1 à posição 2, localizados a distâncias R 1 e R 2 de carga P, . Se o campo for criado por um sistema de cobranças pontuais P 1 ,P 2¼, P n , então a mudança na energia potencial da carga q nesta área:
. No movimento de carga final q da posição 1 à posição 2, localizados a distâncias R 1 e R 2 de carga P, . Se o campo for criado por um sistema de cobranças pontuais P 1 ,P 2¼, P n , então a mudança na energia potencial da carga q nesta área:  . As fórmulas fornecidas nos permitem encontrar apenas mudar energia potencial de uma carga pontual q, e não a energia potencial em si. Para determinar a energia potencial, é necessário concordar em que ponto do campo ela deve ser considerada igual a zero. Para a energia potencial de uma carga pontual q localizado em um campo elétrico criado por outra carga pontual P, Nós temos
. As fórmulas fornecidas nos permitem encontrar apenas mudar energia potencial de uma carga pontual q, e não a energia potencial em si. Para determinar a energia potencial, é necessário concordar em que ponto do campo ela deve ser considerada igual a zero. Para a energia potencial de uma carga pontual q localizado em um campo elétrico criado por outra carga pontual P, Nós temos
![]() , Onde C– constante arbitrária. Deixe a energia potencial ser zero a uma distância infinitamente grande da carga P(no R® ¥), então a constante C= 0 e a expressão anterior assume a forma . Neste caso, a energia potencial é definida como o trabalho de mover uma carga por forças de campo de um determinado ponto para um ponto infinitamente distante.No caso de um campo elétrico criado por um sistema de cargas pontuais, a energia potencial da carga q:
, Onde C– constante arbitrária. Deixe a energia potencial ser zero a uma distância infinitamente grande da carga P(no R® ¥), então a constante C= 0 e a expressão anterior assume a forma . Neste caso, a energia potencial é definida como o trabalho de mover uma carga por forças de campo de um determinado ponto para um ponto infinitamente distante.No caso de um campo elétrico criado por um sistema de cargas pontuais, a energia potencial da carga q:
![]() .
.
![]() Energia potencial de um sistema de cargas pontuais. No caso de um campo eletrostático, a energia potencial serve como medida da interação de cargas. Que haja um sistema de cargas pontuais no espaço Qi(eu = 1, 2, ... , n). A energia da interação de todos n encargos é determinado pela relação, onde r ij - a distância entre as cargas correspondentes, e a soma é realizada de forma que a interação entre cada par de cargas seja levada em consideração uma vez.
Energia potencial de um sistema de cargas pontuais. No caso de um campo eletrostático, a energia potencial serve como medida da interação de cargas. Que haja um sistema de cargas pontuais no espaço Qi(eu = 1, 2, ... , n). A energia da interação de todos n encargos é determinado pela relação, onde r ij - a distância entre as cargas correspondentes, e a soma é realizada de forma que a interação entre cada par de cargas seja levada em consideração uma vez.
Potencial de campo eletrostático. O campo de uma força conservativa pode ser descrito não apenas por uma função vetorial, mas uma descrição equivalente deste campo pode ser obtida definindo uma quantidade escalar adequada em cada um dos seus pontos. Para um campo eletrostático, esta quantidade é potencial de campo eletrostático, definido como a razão entre a energia potencial da carga de teste q para a magnitude desta carga, j = C P/ q, do qual se segue que o potencial é numericamente igual à energia potencial possuída por uma carga positiva unitária em um determinado ponto do campo. A unidade de medida do potencial é o Volt (1 V).
Potencial de campo de carga pontualP em meio isotrópico homogêneo com constante dielétrica e: .
![]()
![]() Princípio da superposição. O potencial é uma função escalar; o princípio da superposição é válido para ele. Então, para o potencial de campo de um sistema de cargas pontuais P 1, P 2¼, Qn temos onde eu- distância de um ponto de campo com potencial j até a carga Qi. Se a carga for distribuída arbitrariamente no espaço, então onde R- distância do volume elementar d x,d sim,d z apontar ( x, sim, z), onde o potencial é determinado; V- o volume do espaço em que a carga é distribuída.
Princípio da superposição. O potencial é uma função escalar; o princípio da superposição é válido para ele. Então, para o potencial de campo de um sistema de cargas pontuais P 1, P 2¼, Qn temos onde eu- distância de um ponto de campo com potencial j até a carga Qi. Se a carga for distribuída arbitrariamente no espaço, então onde R- distância do volume elementar d x,d sim,d z apontar ( x, sim, z), onde o potencial é determinado; V- o volume do espaço em que a carga é distribuída.
Potencial e trabalho das forças do campo elétrico. Com base na definição de potencial, pode-se mostrar que o trabalho realizado pelas forças do campo elétrico ao mover uma carga pontual q de um ponto a outro do campo é igual ao produto da magnitude dessa carga e a diferença de potencial nos pontos inicial e final do caminho, UMA=q(j 1 - j 2).
É conveniente escrever a definição da seguinte forma:
Pergunta nº 4
Para estabelecer uma conexão entre a força característica do campo elétrico - tensão e suas características energéticas - potencial Consideremos o trabalho elementar das forças do campo elétrico em um deslocamento infinitesimal de uma carga pontual q:d UMA=qE d eu, o mesmo trabalho é igual à diminuição da energia potencial da carga q:d UMA = - d C P = - q d, onde d é a mudança no potencial do campo elétrico ao longo do comprimento do percurso d eu. Igualando os lados direitos das expressões, obtemos: E d eu= -d ou no sistema de coordenadas cartesianas
E x d x + E y d y + E z d z =-d, (1.8)
Onde E x,E-e,Ez- projeções do vetor tensão nos eixos do sistema de coordenadas. Como a expressão (1.8) é um diferencial total, então para as projeções do vetor intensidade temos
![]() onde .
onde .
A expressão entre parênteses é gradiente potencial j, ou seja,
E= -grad = -Ñ .
A intensidade em qualquer ponto do campo elétrico é igual ao gradiente de potencial neste ponto, tomado com sinal oposto. O sinal negativo indica que a tensão E direcionado para a diminuição do potencial.
Considere o campo elétrico criado por uma carga pontual positiva q(Fig. 1.6). Potencial de campo em um ponto M, cuja posição é determinada pelo vetor raio R, igual = q/4pe 0e R. Direção do vetor raio R coincide com a direção do vetor de tensão E, e o gradiente potencial é direcionado na direção oposta. Projeção do gradiente na direção do vetor raio
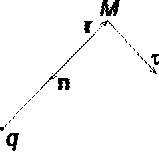
![]() . A projeção do gradiente potencial na direção do vetor t, perpendicular ao vetor R, é igual
. A projeção do gradiente potencial na direção do vetor t, perpendicular ao vetor R, é igual ![]() ,
,
ou seja, nesta direção o potencial do campo elétrico é valor constante(= const).
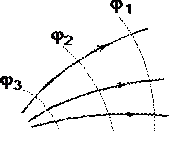 No caso considerado, a direção do vetor R coincide com a direção
No caso considerado, a direção do vetor R coincide com a direção
linhas de energia. Resumindo o resultado obtido, pode-se afirmar que em todos os pontos da curva ortogonais às linhas de força, o potencial do campo elétrico é o mesmo. O lugar geométrico de pontos com o mesmo potencial é uma superfície equipotencial ortogonal às linhas de força.
Ao representar graficamente campos elétricos, superfícies equipotenciais são frequentemente usadas. Normalmente, os equipotenciais são desenhados de tal forma que a diferença de potencial entre quaisquer duas superfícies equipotenciais seja a mesma. Aqui está uma imagem bidimensional do campo elétrico. As linhas de campo são mostradas como linhas sólidas, os equipotenciais como linhas tracejadas.
Tal imagem nos permite dizer em que direção o vetor intensidade do campo elétrico está direcionado; onde a tensão é maior, onde é menor; onde uma carga elétrica colocada em um ou outro ponto do campo começará a se mover. Como todos os pontos de uma superfície equipotencial têm o mesmo potencial, mover uma carga ao longo dela não requer trabalho. Isso significa que a força que atua sobre a carga é sempre perpendicular ao deslocamento.
Pergunta nº 5
Se o condutor receber uma carga excessiva, então esta carga distribuído sobre a superfície do condutor. Na verdade, se dentro de um condutor selecionarmos uma superfície fechada arbitrária S, então o fluxo do vetor de intensidade do campo elétrico através desta superfície deve ser igual a zero. Caso contrário, existirá um campo elétrico dentro do condutor, o que levará ao movimento de cargas. Portanto, para que a condição seja satisfeita
A carga elétrica total dentro desta superfície arbitrária deve ser zero.
A intensidade do campo elétrico próximo à superfície de um condutor carregado pode ser determinada usando o teorema de Gauss. Para fazer isso, selecionamos uma pequena área arbitrária d na superfície do condutor S e, considerando-o como base, construímos sobre ele um cilindro com geratriz d eu(Fig. 3.1). Vetor na superfície do condutor E direcionado normal a esta superfície. Portanto, o fluxo vetorial E através da superfície lateral do cilindro devido à pequenez de d eu igual a zero. O fluxo desse vetor pela base inferior do cilindro, localizado dentro do condutor, também é zero, pois não há campo elétrico no interior do condutor. Portanto, o fluxo vetorial E através de toda a superfície do cilindro é igual ao fluxo através dele base superior d S": , onde E n é a projeção do vetor de intensidade do campo elétrico na normal externa n para o site d S. 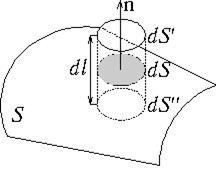
Segundo o teorema de Gauss, esse fluxo é igual à soma algébrica das cargas elétricas cobertas pela superfície do cilindro, dividida pelo produto da constante elétrica e a permissividade relativa do meio que envolve o condutor. Dentro do cilindro existe uma carga, onde é a densidade de carga superficial. Por isso ![]() e, isto é, a intensidade do campo elétrico próximo à superfície de um condutor carregado é diretamente proporcional à densidade superficial das cargas elétricas localizadas nesta superfície.
e, isto é, a intensidade do campo elétrico próximo à superfície de um condutor carregado é diretamente proporcional à densidade superficial das cargas elétricas localizadas nesta superfície.
Estudos experimentais da distribuição de cargas excessivas em condutores várias formas mostrou que a distribuição de cargas na superfície externa do condutor depende apenas da forma da superfície: quanto maior a curvatura da superfície (quanto menor o raio de curvatura), maior a densidade de carga superficial.
Perto de áreas com pequenos raios de curvatura, especialmente perto da ponta, devido aos altos valores de tensão, ocorre a ionização de gases, por exemplo, o ar. Como resultado, íons com a mesma carga do condutor se movem na direção da superfície do condutor, e os íons sinal oposto para a superfície do condutor, o que leva a uma diminuição na carga do condutor. Este fenômeno é denominado drenagem de carga.
Existem cargas excessivas nas superfícies internas de condutores ocos fechados nenhum.
Se um condutor carregado entrar em contato com superfície externa condutor descarregado, então a carga será redistribuída entre os condutores até que seus potenciais se tornem iguais.
Se o mesmo condutor carregado tocar superfície interior condutor oco, então a carga é transferida completamente para o condutor oco.
Concluindo, notamos mais um fenômeno inerente apenas aos condutores. Se um condutor sem carga for colocado em um campo elétrico externo, então suas partes opostas na direção do campo terão cargas de sinais opostos. Se, sem remover o campo externo, o condutor for dividido, as partes separadas terão cargas opostas. Este fenômeno é denominado indução eletrostática.
Pergunta nº 8
Todas as substâncias, de acordo com sua capacidade de conduzir corrente elétrica, são divididas em condutores, dielétricos E semicondutores. Condutores são substâncias nas quais partículas eletricamente carregadas - transportadoras de carga- capaz de mover-se livremente por todo o volume da substância. Os condutores incluem metais, soluções de sais, ácidos e álcalis, sais fundidos, gases ionizados.
Vamos limitar nossa consideração condutores de metal sólido, tendo estrutura de cristal. Experimentos mostram que com uma diferença de potencial muito pequena aplicada a um condutor, os elétrons de condução nele contidos começam a se mover e se mover quase livremente por todo o volume dos metais.
Na ausência de um campo eletrostático externo, os campos elétricos de íons positivos e elétrons de condução são mutuamente compensados, de modo que a intensidade do campo interno resultante é zero.
Ao introduzir um condutor metálico em um campo eletrostático externo com tensão E 0 As forças de Coulomb direcionadas em direções opostas começam a agir sobre íons e elétrons livres. Essas forças provocam o deslocamento de partículas carregadas no interior do metal, e principalmente os elétrons livres são deslocados, e os íons positivos localizados nos nós da rede cristalina praticamente não mudam de posição. Como resultado, um campo elétrico com intensidade de E".
O deslocamento de partículas carregadas dentro do condutor para quando a intensidade total do campo E em um condutor, igual à soma das intensidades dos campos externo e interno, será igual a zero: ![]()
Apresentamos uma expressão conectando a intensidade e o potencial do campo eletrostático da seguinte forma:
Onde E- a intensidade do campo resultante dentro do condutor; n- normal interna à superfície do condutor. Da igualdade a zero da tensão resultante E segue-se que em dentro do volume do condutor, o potencial tem o mesmo valor: .
Os resultados obtidos permitem-nos tirar três conclusões importantes:
1. Em todos os pontos dentro do condutor, a intensidade do campo, ou seja, todo o volume do condutor equipotencial.
2. Com uma distribuição estática de cargas ao longo de um condutor, o vetor de tensão E em sua superfície deve ser direcionado normal à superfície, caso contrário, sob a influência dos componentes de tensão tangentes à superfície do condutor, as cargas devem se mover ao longo do condutor.
3. A superfície do condutor também é equipotencial, pois para qualquer ponto da superfície
![]()
Pergunta nº 10
Se dois condutores têm uma forma tal que o campo elétrico que eles criam está concentrado em uma área limitada do espaço, então o sistema formado por eles é chamado capacitor, e os próprios condutores chamam forros capacitor.
Capacitor esférico. Dois condutores em forma de esferas concêntricas com raios R 1 e R 2 (R 2 > R 1), formam um capacitor esférico. Usando o teorema de Gauss é fácil mostrar que o campo elétrico existe apenas no espaço entre as esferas. A força deste campo ![]() ,
,
Onde q- carga elétrica da esfera interna; - constante dielétrica relativa do meio que preenche o espaço entre as placas; R- distância do centro das esferas, e R 1 r R 2. Diferença potencial entre placas  e a capacitância de um capacitor esférico.
e a capacitância de um capacitor esférico.
Capacitor cilíndrico consiste em dois cilindros coaxiais condutores com raios R 1 e R 2 (R 2 > R 1). Desprezando os efeitos de borda nas extremidades dos cilindros e assumindo que o espaço entre as placas é preenchido com um meio dielétrico com permeabilidade relativa, a intensidade do campo dentro do capacitor pode ser encontrada pela fórmula: ![]() ,
,
Onde q- carga do cilindro interno; h- altura dos cilindros (revestimentos); R- distância do eixo do cilindro. Assim, a diferença de potencial entre as placas de um capacitor cilíndrico e sua capacitância é 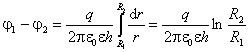 . .
. .
Capacitor plano. Duas placas planas paralelas de mesma área S localizado a uma distância d um do outro, formar capacitor plano. Se o espaço entre as placas for preenchido com um meio com uma constante dielétrica relativa, então quando uma carga for transmitida a elas q a intensidade do campo elétrico entre as placas é igual a, a diferença de potencial é igual a. Assim, a capacitância de um capacitor de placas paralelas é
Conexão em série e paralelo de capacitores.
No conexão serial n capacitores, a capacidade total do sistema é igual a
Conexão paralela n capacitores formam um sistema cuja capacidade elétrica pode ser calculada da seguinte forma:
Pergunta nº 11
Energia de um condutor carregado. A superfície do condutor é equipotencial. Portanto, os potenciais daqueles pontos nos quais as cargas pontuais estão localizadas d q, são idênticos e iguais ao potencial do condutor. Cobrar q, localizado no condutor, pode ser considerado como um sistema de cargas pontuais d q. Então a energia do condutor carregado
Levando em consideração a definição de capacitância, podemos escrever
Qualquer uma dessas expressões determina a energia de um condutor carregado.
Energia de um capacitor carregado. Deixe o potencial da placa do capacitor na qual a carga é + q, é igual a , e o potencial da placa na qual a carga está localizada é q, é igual a . A energia de tal sistema
A energia de um capacitor carregado pode ser representada como
Energia do campo elétrico. A energia de um capacitor carregado pode ser expressa em termos de quantidades que caracterizam o campo elétrico no espaço entre as placas. Vamos fazer isso usando o exemplo de um capacitor plano. Substituindo a expressão da capacitância na fórmula da energia do capacitor dá
Privado você / d igual à intensidade do campo na lacuna; trabalhar S· d representa o volume V ocupada pelo campo. Por isso, ![]()
Se o campo for uniforme (que é o caso de um capacitor plano a uma distância d muito menor que as dimensões lineares das placas), então a energia nela contida é distribuída no espaço com densidade constante c. Então densidade de energia volumétrica campo elétrico é igual
![]()
Levando em conta a relação, podemos escrever
Em um dielétrico isotrópico, as direções dos vetores D E E coincidir e
Substituindo a expressão, obtemos
O primeiro termo nesta expressão coincide com a densidade de energia do campo no vácuo. O segundo termo representa a energia gasta na polarização do dielétrico. Vamos demonstrar isso usando o exemplo de um dielétrico apolar. A polarização de um dielétrico apolar consiste no fato de que as cargas que compõem as moléculas são deslocadas de suas posições sob a influência de um campo elétrico E. Por unidade de volume de dielétrico, trabalho gasto no deslocamento de cargas q eu por valor d R eu, é
A expressão entre parênteses é o momento dipolar por unidade de volume ou a polarização do dielétrico R. Por isso, .
Vetor P associado a um vetor E razão Substituindo esta expressão na fórmula do trabalho, obtemos
Feita a integração, determinamos o trabalho gasto na polarização de uma unidade de volume do dielétrico.
Conhecendo a densidade de energia do campo em cada ponto, você pode encontrar a energia do campo contida em qualquer volume V. Para fazer isso, você precisa calcular a integral: ![]()
Densidade de energia do campo eletrostático
Utilizando (66), (50), (53), transformamos a fórmula da energia do capacitor da seguinte forma: , onde está o volume do capacitor. Vamos dividir a última expressão por: ![]() . O valor tem o significado da densidade de energia do campo eletrostático.
. O valor tem o significado da densidade de energia do campo eletrostático.
Pergunta nº 12
Um dielétrico colocado em um campo elétrico externo polariza sob a influência deste campo. A polarização de um dielétrico é o processo de aquisição de um momento dipolar macroscópico diferente de zero.
O grau de polarização de um dielétrico é caracterizado por uma grandeza vetorial chamada polarização ou vetor de polarização (P). A polarização é definida como o momento elétrico por unidade de volume do dielétrico,
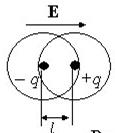 Onde N- número de moléculas em volume. Polarização P frequentemente chamada de polarização, significando com isso uma medida quantitativa desse processo.
Onde N- número de moléculas em volume. Polarização P frequentemente chamada de polarização, significando com isso uma medida quantitativa desse processo.
Nos dielétricos, distinguem-se os seguintes tipos de polarização: eletrônica, orientacional e reticular (para cristais iônicos).
Tipo de polarização eletrônica característica de dielétricos com moléculas apolares. Em um campo elétrico externo, as cargas positivas dentro da molécula são deslocadas na direção do campo, e as cargas negativas na direção oposta, como resultado as moléculas adquirem um momento dipolar direcionado ao longo do campo externo
 O momento dipolar induzido de uma molécula é proporcional à força do campo elétrico externo, onde está a polarizabilidade da molécula. O valor de polarização neste caso é igual a, onde n- concentração de moléculas; - o momento dipolar induzido de uma molécula, que é o mesmo para todas as moléculas e cuja direção coincide com a direção do campo externo.
O momento dipolar induzido de uma molécula é proporcional à força do campo elétrico externo, onde está a polarizabilidade da molécula. O valor de polarização neste caso é igual a, onde n- concentração de moléculas; - o momento dipolar induzido de uma molécula, que é o mesmo para todas as moléculas e cuja direção coincide com a direção do campo externo.
Tipo de orientação de polarização característica dos dielétricos polares. Na ausência de um campo elétrico externo, os dipolos moleculares são orientados aleatoriamente, de modo que o momento elétrico macroscópico do dielétrico é zero.
 Se colocarmos tal dielétrico em um campo elétrico externo, então um momento de força atuará sobre a molécula dipolo (Fig. 2.2), tendendo a orientar seu momento dipolar na direção da intensidade do campo. Porém, a orientação completa não ocorre, uma vez que o movimento térmico tende a destruir o efeito do campo elétrico externo.
Se colocarmos tal dielétrico em um campo elétrico externo, então um momento de força atuará sobre a molécula dipolo (Fig. 2.2), tendendo a orientar seu momento dipolar na direção da intensidade do campo. Porém, a orientação completa não ocorre, uma vez que o movimento térmico tende a destruir o efeito do campo elétrico externo.
Essa polarização é chamada de orientacional. A polarização neste caso é igual a, onde<p> é o valor médio da componente do momento dipolar da molécula na direção do campo externo.
Tipo de polarização de grade característica dos cristais iônicos. Em cristais iônicos (NaCl, etc.) na ausência de um campo externo, o momento dipolar de cada célula unitária é zero (Fig. 2.3.a), sob a influência de um campo elétrico externo, íons positivos e negativos são deslocados em direções opostas (Fig. 2.3.b). Cada célula do cristal torna-se um dipolo, o cristal é polarizado. Essa polarização é chamada treliça. A polarização, neste caso, também pode ser definida como, onde é o valor do momento dipolar da célula unitária, n- número de células por unidade de volume.
A polarização de dielétricos isotrópicos de qualquer tipo está relacionada à intensidade do campo pela relação, onde - suscetibilidade dielétrica dielétrico.
Pergunta nº 13
A polarização de um meio tem uma propriedade notável: o fluxo do vetor de polarização do meio através de uma superfície fechada arbitrária é numericamente igual ao valor das cargas “ligadas” não compensadas dentro desta superfície, tomadas com o sinal oposto:
![]() (1). Na formulação local, a propriedade descrita é descrita pela relação
(1). Na formulação local, a propriedade descrita é descrita pela relação
(2), onde é a densidade de volume das cargas “ligadas”. Essas relações são chamadas de teorema de Gauss para a polarização do meio (vetor de polarização) nas formas integral e diferencial, respectivamente. Se o teorema de Gauss para a intensidade do campo elétrico é uma consequência da lei de Coulomb na forma de "campo", então o teorema de Gauss para a polarização é uma consequência da definição desta quantidade.
Vamos provar a relação (1), então a relação (2) será válida devido ao teorema matemático de Ostrogradsky-Gauss.
Consideremos um dielétrico de moléculas apolares com uma concentração volumétrica destas últimas igual a. Acreditamos que, sob a influência de um campo elétrico, as cargas positivas se deslocaram da posição de equilíbrio em uma quantidade e as cargas negativas em uma quantidade. Cada molécula adquiriu um momento elétrico ![]() , e o volume unitário adquiriu um momento elétrico. Consideremos uma superfície fechada arbitrária suficientemente lisa no dielétrico que está sendo descrito. Suponhamos que a superfície seja desenhada de tal forma que na ausência de campo elétrico ela “não atravessa” dipolos individuais, ou seja, as cargas positivas e negativas associadas à estrutura molecular da substância “compensam” umas às outras .
, e o volume unitário adquiriu um momento elétrico. Consideremos uma superfície fechada arbitrária suficientemente lisa no dielétrico que está sendo descrito. Suponhamos que a superfície seja desenhada de tal forma que na ausência de campo elétrico ela “não atravessa” dipolos individuais, ou seja, as cargas positivas e negativas associadas à estrutura molecular da substância “compensam” umas às outras .
Observe, a propósito, que as relações (1) e (2) para e são satisfeitas de forma idêntica.
Sob a influência de um campo elétrico, um elemento de área superficial será atravessado por cargas positivas do volume na quantidade de. Para cargas negativas temos os valores correspondentes e . A carga total transferida para o lado “externo” do elemento de área de superfície (lembre-se que - a normal externa em relação ao volume coberto pela superfície) é igual a
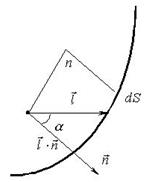
Propriedades do vetor de polarização do meio
Integrando a expressão resultante sobre uma superfície fechada, obtemos o valor da carga elétrica total que saiu do volume considerado. Este último permite-nos concluir que no volume considerado permanece uma carga não compensada - igual em magnitude à carga que partiu. Como resultado temos: ![]() , assim o teorema de Gauss para um campo vetorial na formulação integral é provado.
, assim o teorema de Gauss para um campo vetorial na formulação integral é provado.
Para considerar o caso de uma substância constituída por moléculas polares, basta no raciocínio acima substituir a quantidade pelo seu valor médio.
A prova da validade da relação (1) pode ser considerada completa.
Pergunta nº 14
Cargas elétricas de dois tipos podem estar presentes em um meio dielétrico: “livres” e “ligadas”. Os primeiros não estão relacionados com a estrutura molecular da substância e, via de regra, podem mover-se com relativa liberdade no espaço. Estes últimos estão associados à estrutura molecular da substância e, sob a influência de um campo elétrico, podem ser deslocados da posição de equilíbrio, via de regra, em distâncias muito curtas.
O uso direto do teorema de Gauss para um campo vetorial ao descrever um meio dielétrico é inconveniente porque o lado direito da fórmula
![]() (1), contém tanto o valor das cargas “livres” quanto o valor das cargas “ligadas” (não compensadas) dentro da superfície fechada.
(1), contém tanto o valor das cargas “livres” quanto o valor das cargas “ligadas” (não compensadas) dentro da superfície fechada.
Se a relação (1) for adicionada termo a termo com a relação ![]() , Nós temos
, Nós temos ![]() , (2)
, (2)
onde é a carga “livre” total do volume coberto pela superfície fechada. A relação (2) determina a conveniência de introduzir um vetor especial
Como uma quantidade calculada conveniente que caracteriza o campo elétrico em um meio dielétrico. O vetor era anteriormente chamado de vetor de indução elétrica ou vetor de deslocamento elétrico. O termo "vetor" está atualmente em uso. Para um campo vetorial, a forma integral do teorema de Gauss é válida: ![]() e, consequentemente, a forma diferencial do teorema de Gauss:
e, consequentemente, a forma diferencial do teorema de Gauss:
onde está a densidade de volume de cobranças gratuitas.
Se a relação for válida (para eletretos rígidos não é válida), então para o vetor da definição (3) segue,
onde está a constante dielétrica do meio, uma das características elétricas mais importantes de uma substância. Na eletrostática e na eletrodinâmica quase estacionária, a quantidade é real. Ao considerar processos oscilatórios de alta frequência, a fase de oscilação do vetor e, portanto, do vetor, pode não coincidir com a fase de oscilação do vetor; nesses casos, a quantidade torna-se uma quantidade de valor complexo.
Consideremos a questão em que condições em um meio dielétrico é possível o aparecimento de uma densidade volumétrica descompensada de cargas ligadas. Para tanto, escrevemos a expressão para o vetor de polarização em termos da constante dielétrica do meio e do vetor:
A validade disso é fácil de verificar. A quantidade de juros agora pode ser calculada:
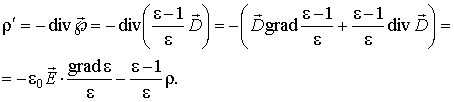 (3)
(3)
Na ausência de densidade volumétrica de cargas livres em um meio dielétrico, o valor pode se tornar zero se
a) o campo está faltando; ou b) o meio é homogêneo ou c) os vetores e são ortogonais. No caso geral, é necessário calcular o valor através das relações (3).
Pergunta nº 17
 Vamos considerar o comportamento dos vetores E E D na interface entre dois dielétricos isotrópicos homogêneos com permeabilidades e na ausência de cargas livres na interface.
Vamos considerar o comportamento dos vetores E E D na interface entre dois dielétricos isotrópicos homogêneos com permeabilidades e na ausência de cargas livres na interface.
Condições de contorno para os componentes normais dos vetores D e E siga o teorema de Gauss. Selecionemos uma superfície fechada em forma de cilindro próximo à interface, cuja geratriz é perpendicular à interface e as bases estão a uma distância igual da interface.
Como não há cargas livres na interface entre os dielétricos, então, de acordo com o teorema de Gauss, o fluxo do vetor de indução elétrica através dada superfície
Isolamento de fluxos através das bases e superfície lateral do cilindro
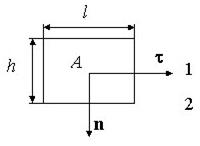 , onde é o valor médio da componente tangente sobre a superfície lateral. Passando ao limite em (neste caso também tende a zero), obtemos
, onde é o valor médio da componente tangente sobre a superfície lateral. Passando ao limite em (neste caso também tende a zero), obtemos ![]() , ou finalmente para os componentes normais do vetor de indução elétrica. Para os componentes normais do vetor de intensidade de campo obtemos
, ou finalmente para os componentes normais do vetor de indução elétrica. Para os componentes normais do vetor de intensidade de campo obtemos ![]() . Assim, ao passar pela interface entre meios dielétricos, a componente normal do vetor sofre brecha, e o componente normal do vetor contínuo.
. Assim, ao passar pela interface entre meios dielétricos, a componente normal do vetor sofre brecha, e o componente normal do vetor contínuo.
Condições de contorno para os componentes tangentes dos vetores D e E segue da relação que descreve a circulação do vetor de intensidade do campo elétrico. Vamos construir um contorno retangular fechado de comprimento próximo à interface eu e alturas h. Considerando isso para o campo eletrostático, e percorrendo o contorno no sentido horário, imaginemos a circulação do vetor E no seguinte formato: ![]() ,
,
onde está o valor médio E n nas laterais do retângulo. Passando ao limite em , obtemos para as componentes tangenciais E .
Para as componentes tangenciais do vetor de indução elétrica, a condição de contorno tem a forma ![]()
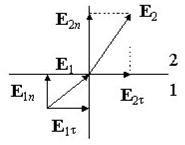 Assim, ao passar pela interface entre meios dielétricos, a componente tangencial do vetor contínuo, e a componente tangente do vetor sofre brecha.
Assim, ao passar pela interface entre meios dielétricos, a componente tangencial do vetor contínuo, e a componente tangente do vetor sofre brecha.
Refração de linhas de campo elétrico. Das condições de contorno para os vetores componentes correspondentes E E D segue-se que ao cruzar a interface entre dois meios dielétricos, as linhas desses vetores são refratadas (Fig. 2.8). Vamos expandir os vetores E1 E E2 na interface em componentes normais e tangenciais e determine a relação entre os ângulos e sob a condição. É fácil ver que a mesma lei de refração das linhas de tensão e das linhas de deslocamento é válida tanto para a intensidade do campo quanto para a indução.
![]() .
.
Ao passar para um meio com valor inferior, o ângulo formado pelas linhas de tensão (deslocamento) com a normal diminui, portanto, as linhas se localizam com menor frequência. Ao passar para um ambiente a partir de uma linha maior de vetores E E D, pelo contrário, são condensados e saindo do normal.
Pergunta nº 6
Teorema sobre a unicidade das soluções para problemas eletrostáticos (dada a localização dos condutores e suas cargas).
Se a localização dos condutores no espaço e a carga total de cada um dos condutores forem fornecidas, então o vetor da intensidade do campo eletrostático em cada ponto é determinado de forma única. Documento: (por contradição)
Deixe a carga nos condutores ser distribuída da seguinte forma:
Suponhamos que não só isso, mas também uma distribuição de carga diferente dela seja possível:
(isto é, difere tão pouco quanto desejado em pelo menos um condutor)
Isso significa que pelo menos em um ponto do espaço outro vetor E será encontrado, ou seja, perto de novos valores de densidade, pelo menos em alguns pontos E será excelente. Que. com o mesmo condições iniciais, com os mesmos condutores obtemos uma solução diferente. Agora vamos mudar o sinal da carga para o oposto.
(o sinal deve ser alterado em todos os condutores de uma vez)
Neste caso, a aparência das linhas de campo não mudará (não contradiz nem o teorema de Gauss nem o teorema da circulação), apenas a sua direção e o vetor E mudarão.
Agora vamos fazer uma superposição de cobranças (uma combinação de duas opções de cobrança):
(ou seja, vamos colocar uma carga em cima da outra e carregá-la da 3ª maneira)
Se não coincidir pelo menos em algum lugar com , então pelo menos em um lugar obteremos algum
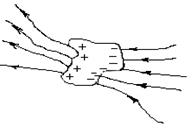 3) levamos as linhas ao infinito sem fechá-las no condutor. neste caso fechamos o contorno fechado L no infinito. Mas mesmo neste caso, ignorando linha de energia não dará circulação zero.
3) levamos as linhas ao infinito sem fechá-las no condutor. neste caso fechamos o contorno fechado L no infinito. Mas mesmo neste caso, ignorando linha de energia não dará circulação zero.
Conclusão: isso significa que não pode ser diferente de zero, o que significa que a distribuição das cobranças é estabelecida de forma única -> a singularidade da solução, ou seja, E – encontramos isso de uma forma única.
Pergunta nº 7
Bilhete 7. Teorema sobre a singularidade das soluções para problemas eletrostáticos. (as localizações dos condutores e seus potenciais são especificados). Se a localização dos condutores e o potencial de cada um deles forem fornecidos, então a intensidade do campo eletrostático em cada ponto poderá ser encontrada de uma forma única.
(Curso de Berkeley)
Em todos os lugares fora do condutor a função deve satisfazer a equação diferencial parcial: , ou, caso contrário, (2)
É óbvio que W não satisfaz as condições de contorno. Na superfície de cada condutor, a função W é igual a zero, pois assumem o mesmo valor na superfície do condutor. Portanto W é uma solução para outro problema eletrostático, com os mesmos condutores, mas sob a condição de que todos os condutores tenham potencial zero. Se for assim, podemos dizer que a função W é igual a zero em todos os pontos do espaço. Se não for esse o caso, então deve haver um máximo ou um mínimo em algum lugar. O caminho W tem um extremo no ponto P; então considere uma bola com centro neste ponto. Sabemos que o valor médio sobre a esfera de uma função que satisfaz a equação de Laplace é igual ao valor da função no centro. É injusto que o centro seja o máximo ou o mínimo desta função. Assim, W não pode ter máximo ou mínimo; deve ser igual a zero em todos os lugares. Segue-se que =
Pergunta nº 28
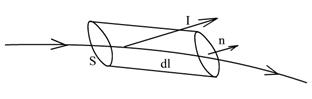 Trm. sobre circulação EU.
Trm. sobre circulação EU.
I é o vetor de magnetização. Eu = = N p 1 m = N n eu 1 S\c
DV = Sdl cosα; di mol = i 1 mol NSdl cosα = cIdl cosα, N é o número de mol-l por 1 cm 3. Próximo ao contorno, consideramos a substância homogênea, ou seja, todos os dipolos, todas as moléculas possuem o mesmo momento magnético. Para calcular, tomemos uma molécula cujo núcleo esteja localizado diretamente no contorno dl. Precisamos contar quantos átomos cruzarão o cilindro uma vez => Esses são aqueles cujos centros estão dentro desse cilindro imaginário. Assim, estamos interessados apenas em eu digo – ou seja, corrente atravessando uma superfície apoiada por um contorno.
Pergunta nº 9
1. Energia de um sistema de cargas pontuais estacionárias . As forças eletrostáticas são conservativas e o sistema de cargas possui energia potencial. Deixe as cargas Q 1 e Q 2 estarem a uma distância r uma da outra. Cada uma dessas cargas no campo da outra tem energia potencial
onde φ 12 e φ 21 são, respectivamente, os potenciais criados pela carga Q 2 no ponto onde a carga Q 1 está localizada e vice-versa.
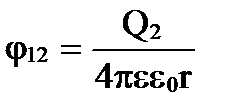 ;
; 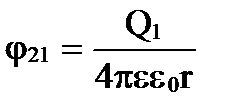 .
.
W 1 = W 2 =W = Q 1 φ 12 = Q 2 φ 21 = ½ (Q 1 φ 12 + Q 2 φ 21).
Ao adicionar cargas Q 3 , Q 4 , ..., Q n sequencialmente a um sistema de duas cargas, pode-se verificar que a energia de interação do sistema de cargas é igual a
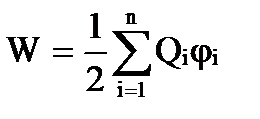 ,
,
onde φ i é o potencial criado no ponto onde a carga Q i está localizada por todas as cargas, exceto a i-ésima.
2. Energia de um condutor solitário carregado . Seja um condutor solitário cuja carga, capacidade e potencial sejam Q, C, φ.
Vamos aumentar a carga em dQ. Para isso, é necessário transferir a carga dQ do infinito para a superfície do condutor, gastando um trabalho igual a
dA = φdQ = C φd φ
Para carregar um corpo de um potencial zero a um potencial igual a φ, é necessário realizar trabalho
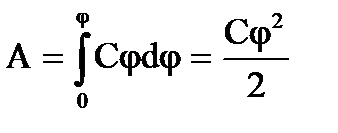
A energia do condutor carregado será igual a este trabalho

Considerando que  , esta energia pode ser representada na forma
, esta energia pode ser representada na forma
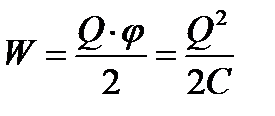
3. Energia de um capacitor carregado . Como qualquer condutor carregado, um capacitor possui energia
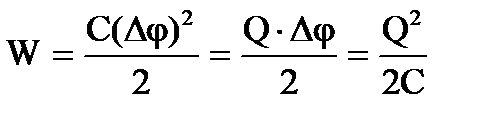
onde Q é a carga do capacitor, C é sua capacidade e Δφ é a diferença de potencial entre as placas.
Usando a expressão para energia, podemos encontrar a força mecânica (ponderomotriz) com a qual as placas do capacitor se atraem. Para fazer isso, suponha que a distância x entre as placas mude na quantidade dx. Então força efetiva funciona igual a
devido a uma diminuição na energia potencial Fdx = - dW, de onde
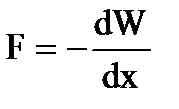 .
.
Substituindo energia na fórmula 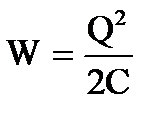 expressão de capacidade
expressão de capacidade
 , Nós temos
, Nós temos
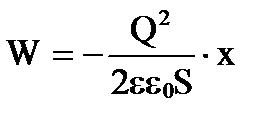 .
.
Diferenciando W em relação a X, vamos encontrar a força F
 ,
,
onde o sinal menos indica que a força F tende a reduzir a distância entre as placas, ou seja, é a força da atração. Substituindo a expressão pela densidade de carga nas placas  , Nós temos
, Nós temos 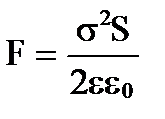 .
.
Considerando a intensidade do campo que E =  , Nós temos
, Nós temos
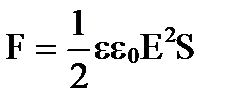 .
.
A pressão nas placas dielétricas colocadas na folga do capacitor será
![]()
4. Energia do campo eletrostático.
Vamos transformar a fórmula da energia de um capacitor plano  , usando fórmulas
, usando fórmulas
 e Δφ = Ed.
e Δφ = Ed.
Nós temos,
onde V é o volume do espaço entre as placas do capacitor no qual está concentrada a energia de seu campo W.
A densidade de energia do campo volumétrico w é a energia contida em uma unidade de volume do campo elétrico e é igual a
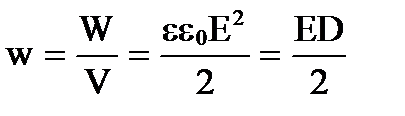 .
.
Unidade de medida [J/m 3 ].
Pode-se observar que a densidade de energia do campo volumétrico depende apenas das características do campo e do meio.

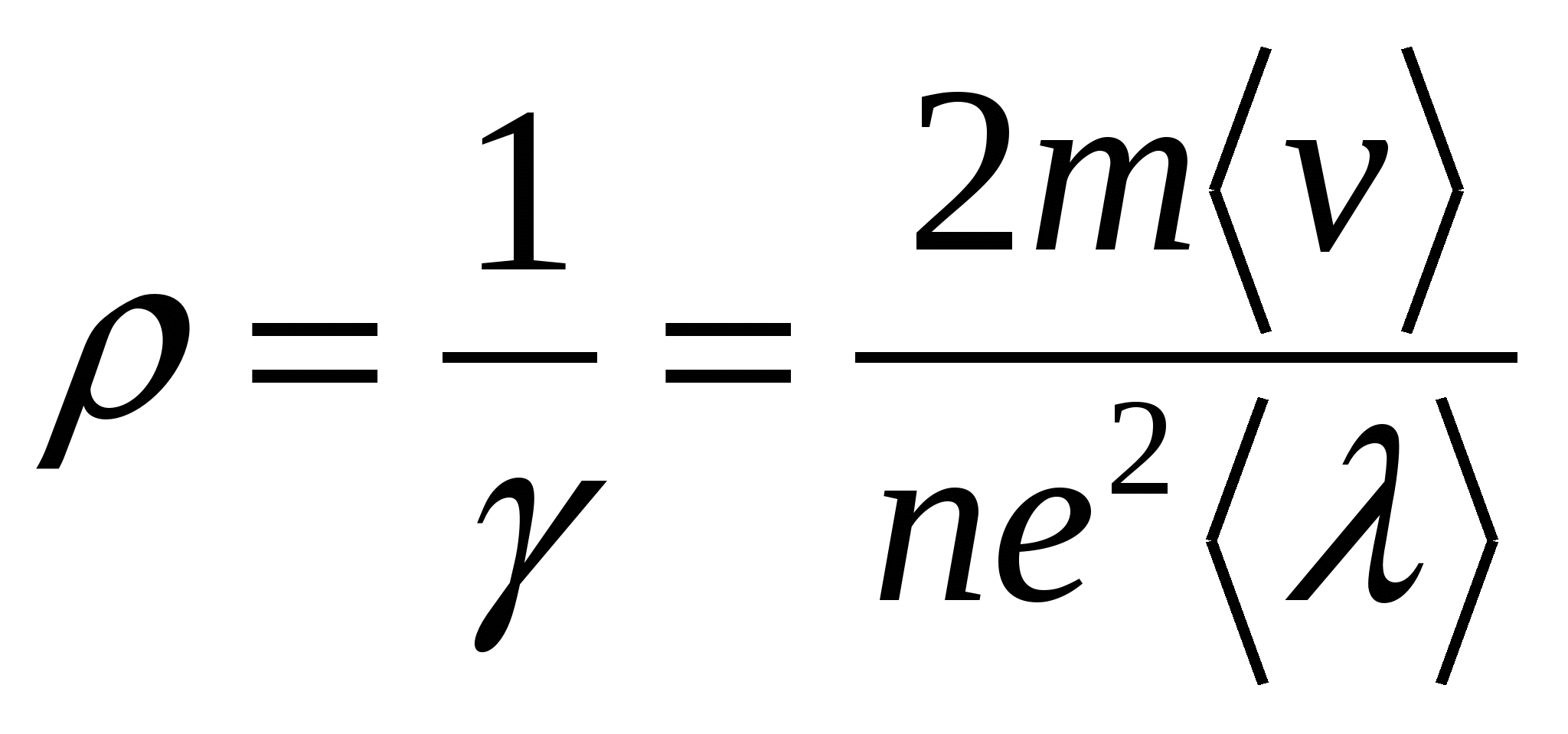 .
. . O elétron transfere completamente essa energia para o íon da rede cristalina ao colidir com ele. Muitas dessas colisões levam à liberação de calor Joule. Se a concentração de elétrons n, e cada um deles enfrenta
. O elétron transfere completamente essa energia para o íon da rede cristalina ao colidir com ele. Muitas dessas colisões levam à liberação de calor Joule. Se a concentração de elétrons n, e cada um deles enfrenta  vezes em 1 s, então a energia será liberada em uma unidade de volume do condutor
vezes em 1 s, então a energia será liberada em uma unidade de volume do condutor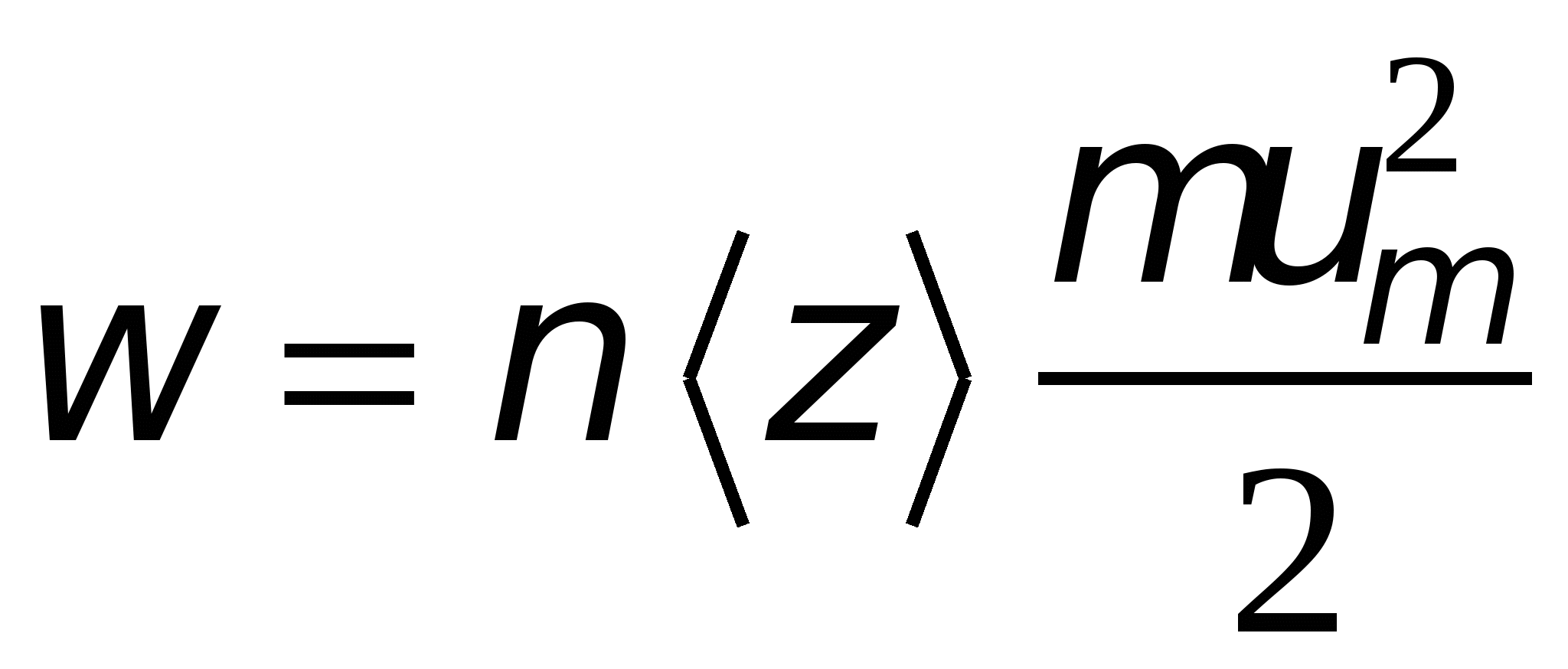 .
.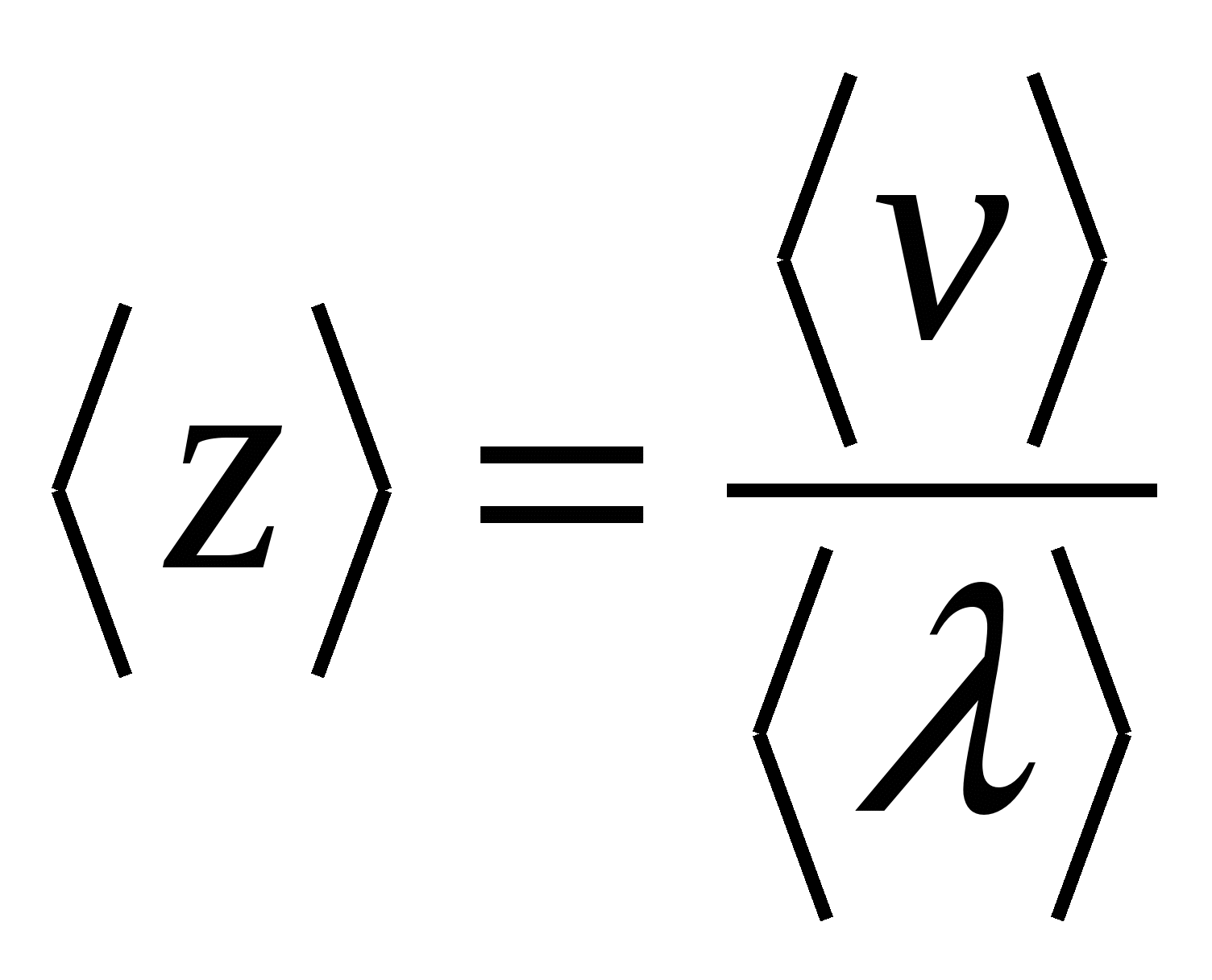 ,
, 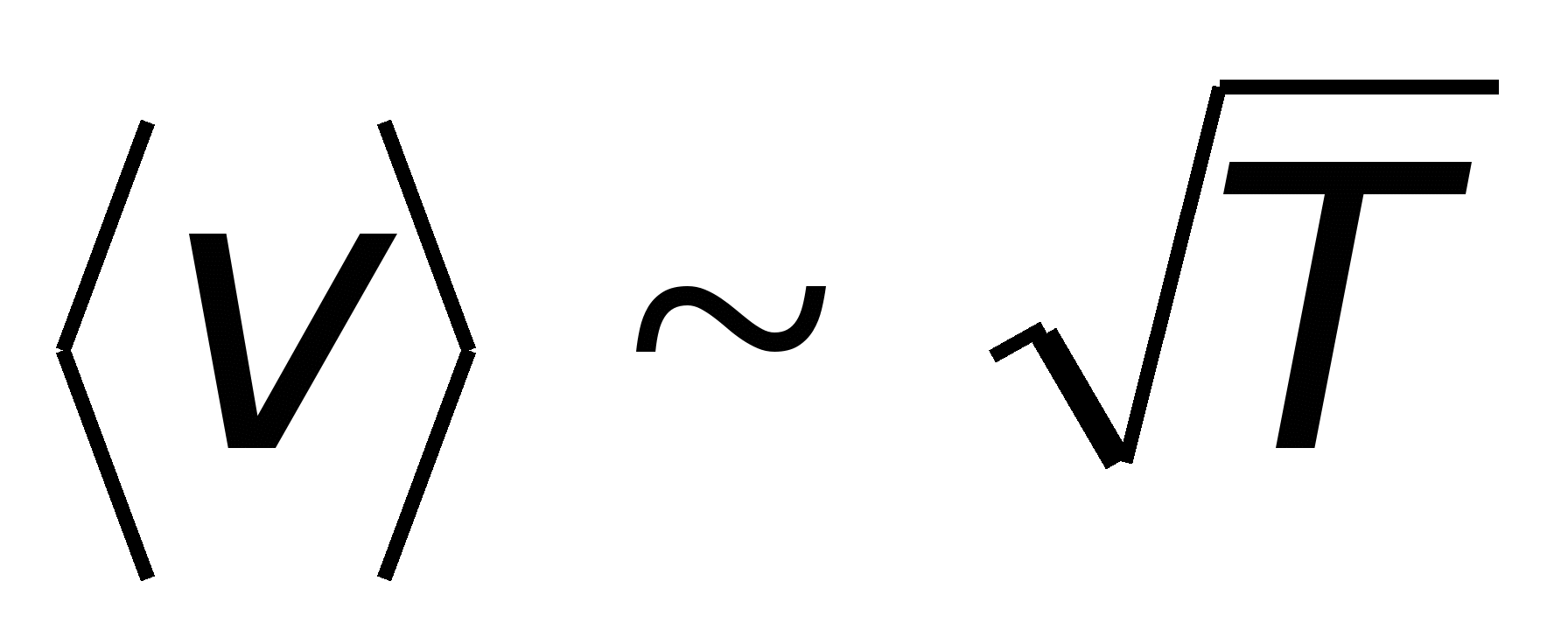 , portanto, resistividade
, portanto, resistividade 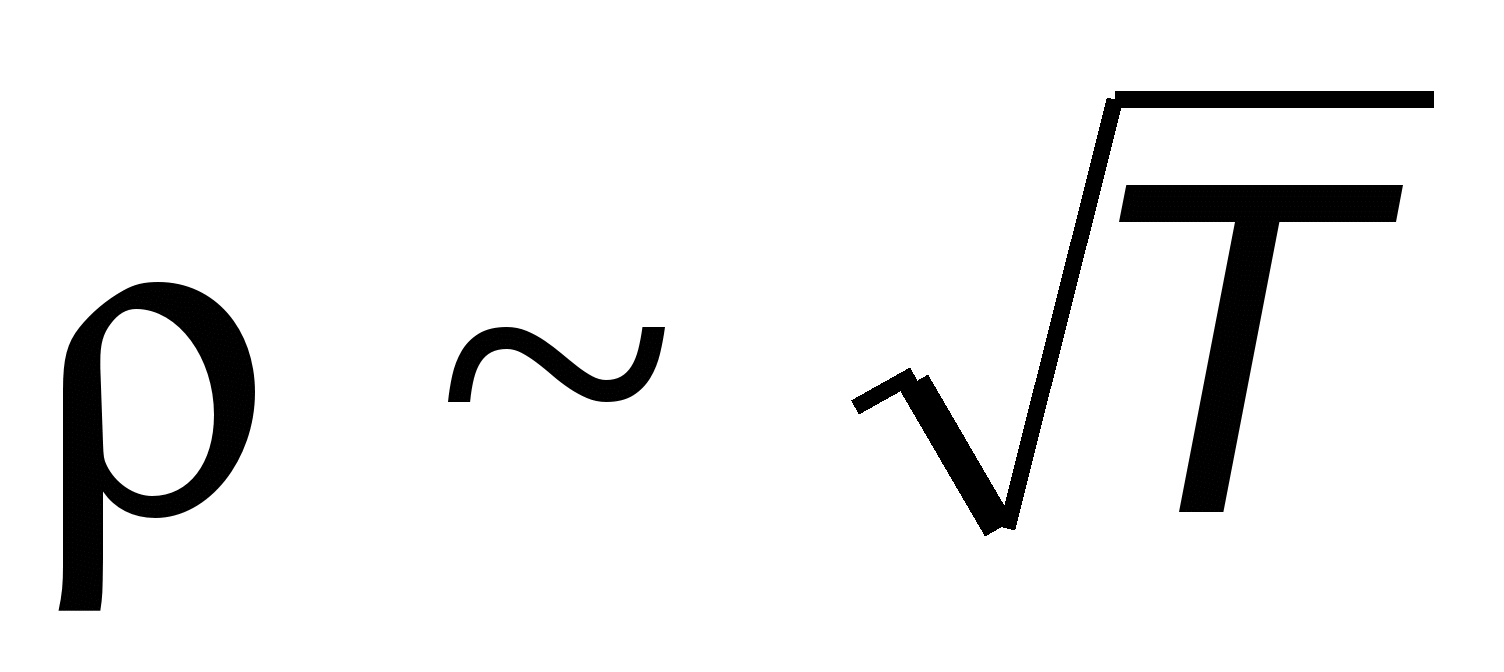 . Entretanto, a experiência mostra que depende linearmente da temperatura
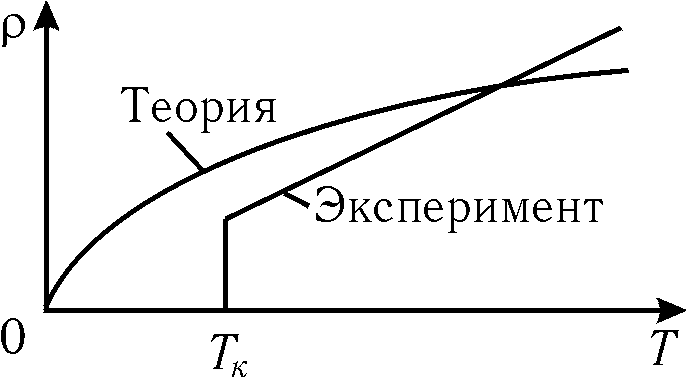
. Entretanto, a experiência mostra que depende linearmente da temperatura 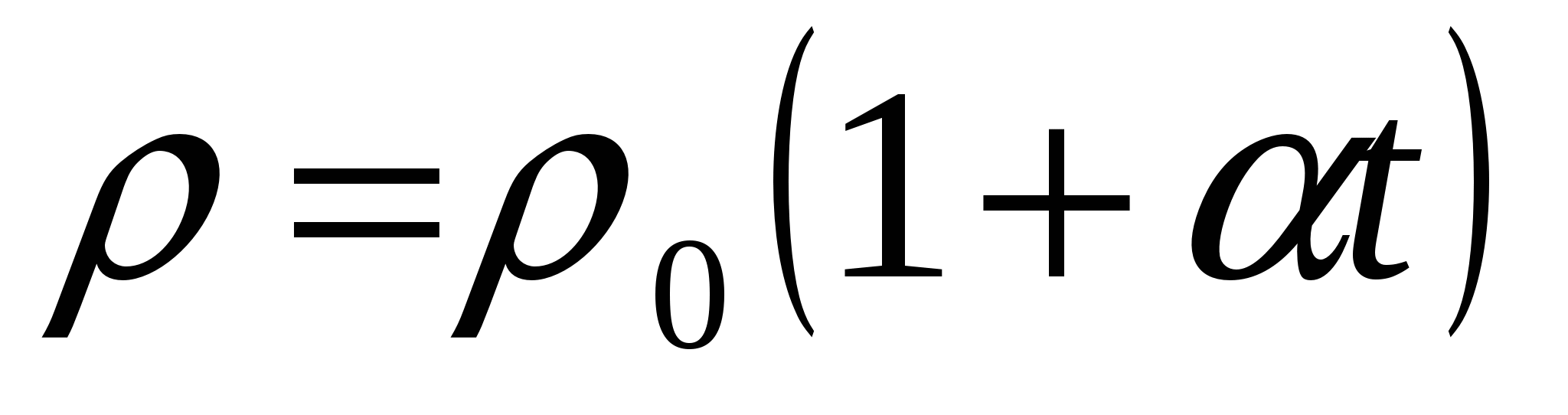 ,
,
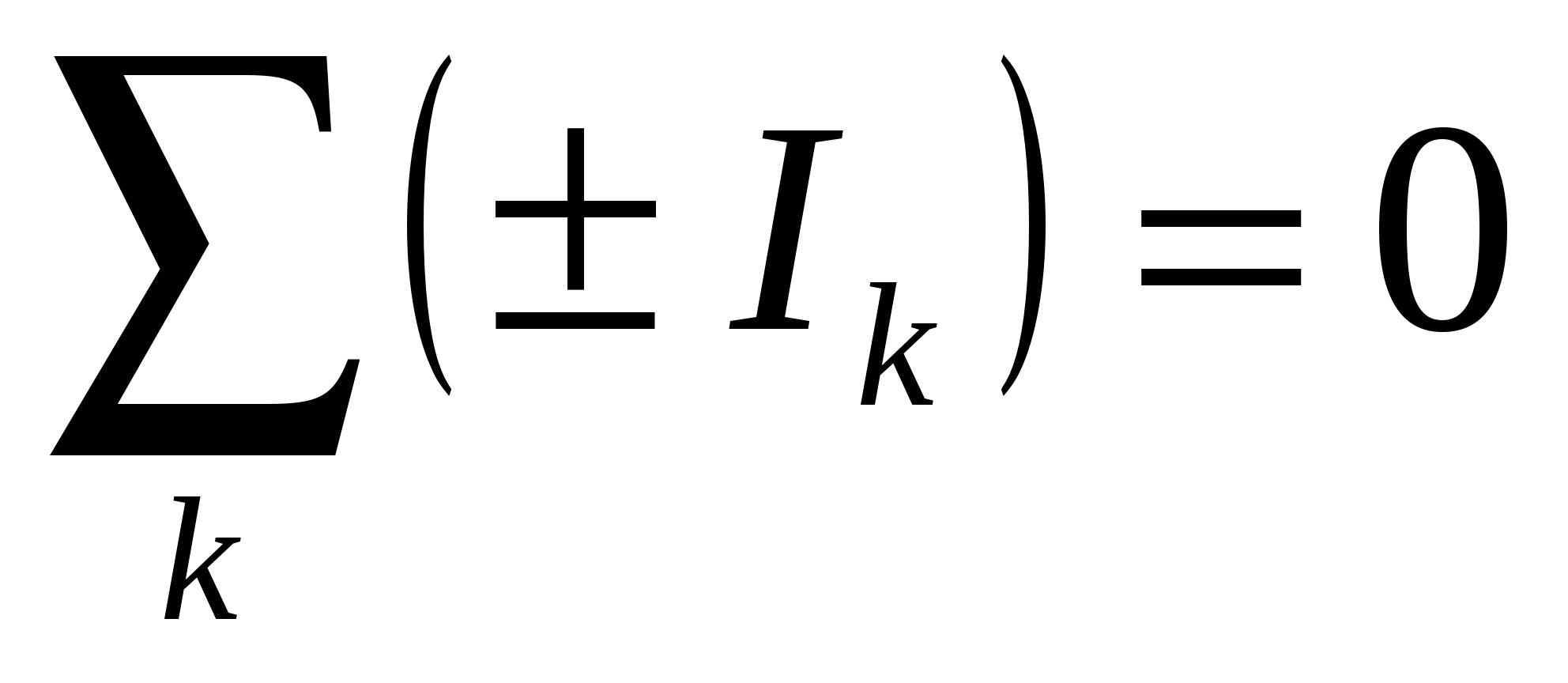 .
.
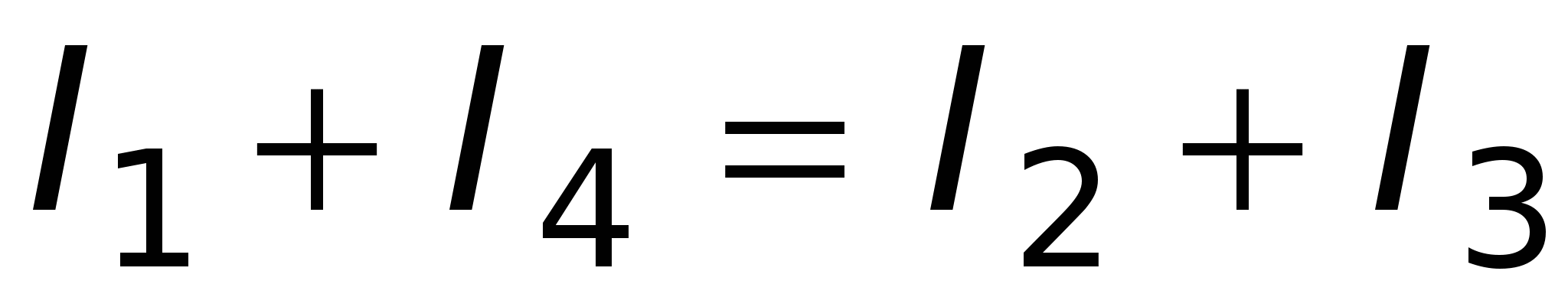 ,
,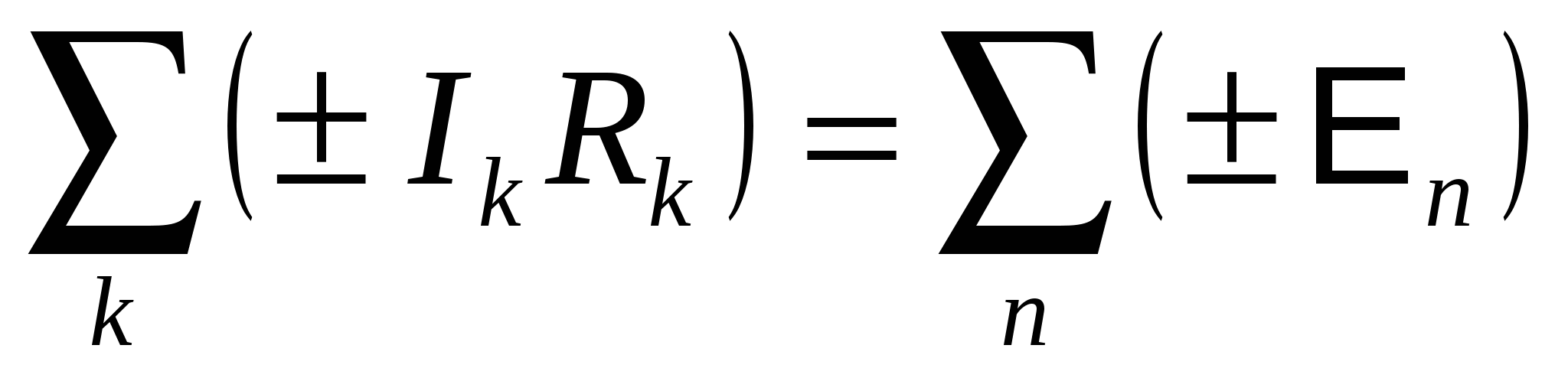 .
.