Densitatea energiei câmpului electric volumetric
14.1. Energia unui sistem de sarcini punctiforme
Orez. 14.1
Dintr-o comparație a (14.1) și (14.2) este clar că Q 1 Q 2 , prin urmare energia unui sistem de două sarcini punctiforme poate fi reprezentată într-o formă simetrică:
unde i– potențial de câmp creat de toate sarcinile, cu excepția i a, în punctul în care se află i-a taxa.
^
14.2. Energia unui conductor încărcat
O sarcină situată pe suprafața unui conductor poate fi considerată ca un sistem de sarcini punctuale, prin urmare, pentru a calcula energia unui conductor încărcat, puteți utiliza formula (14.4). Potențialul oricărui punct de pe suprafața conductorului este același ( i=), deoarece suprafața sa este echipotențială. Prin urmare, în formula (14.4) potențialul poate fi scos din semnul sumei:
 sau
sau  , (14.5) unde
, (14.5) unde 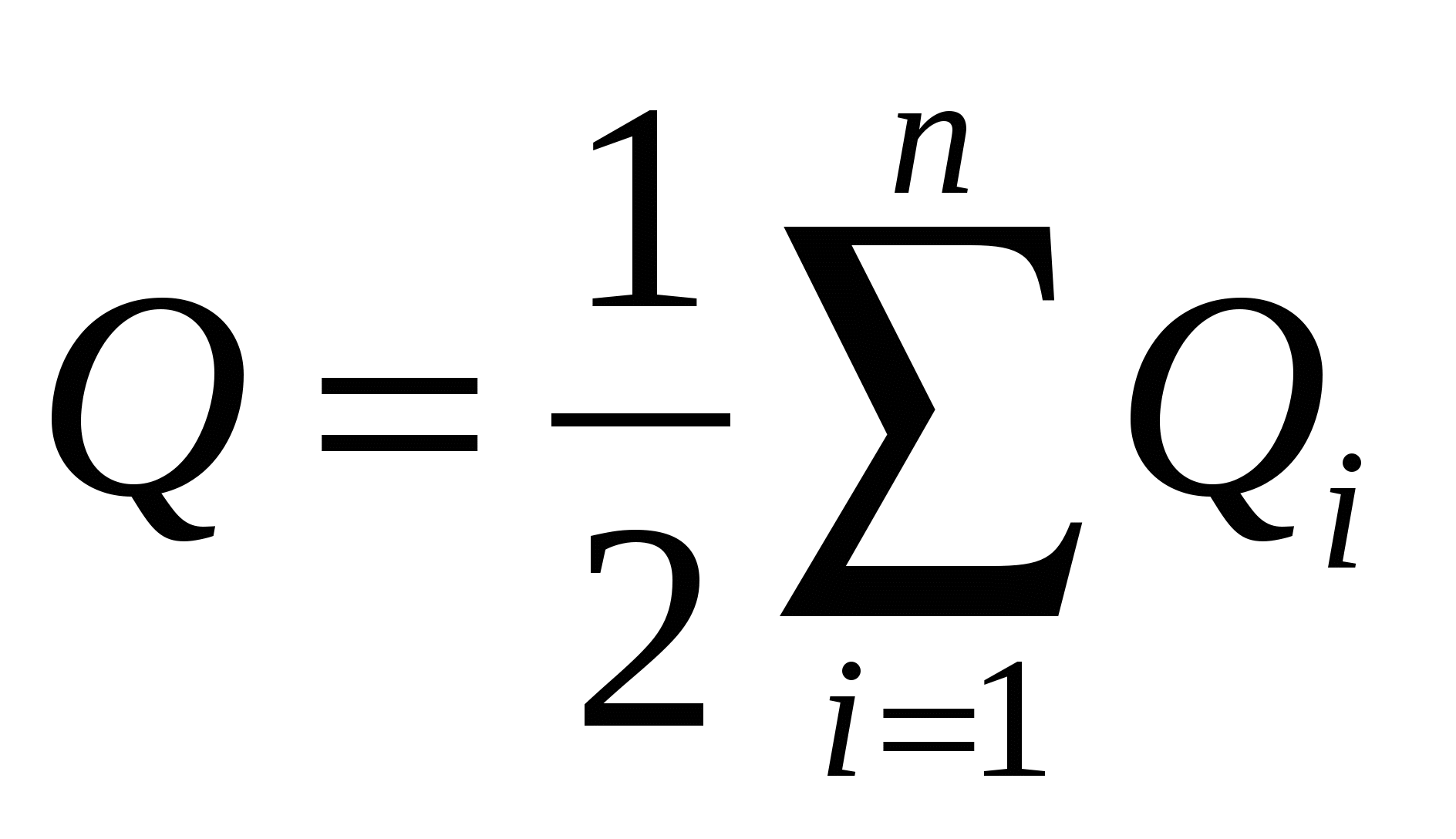 – sarcina conductorului.
– sarcina conductorului.
Ținând cont de (13.3), expresia pentru energia unui conductor încărcat poate fi reprezentată sub forma
^
14.3. Energia unui condensator încărcat. Densitatea energiei câmpului electrostatic
Pentru a calcula energia unui condensator încărcat, folosim formulele (14.5) – (14.7), înlocuind cu diferența de potențial dintre plăcile condensatorului U= . Apoi
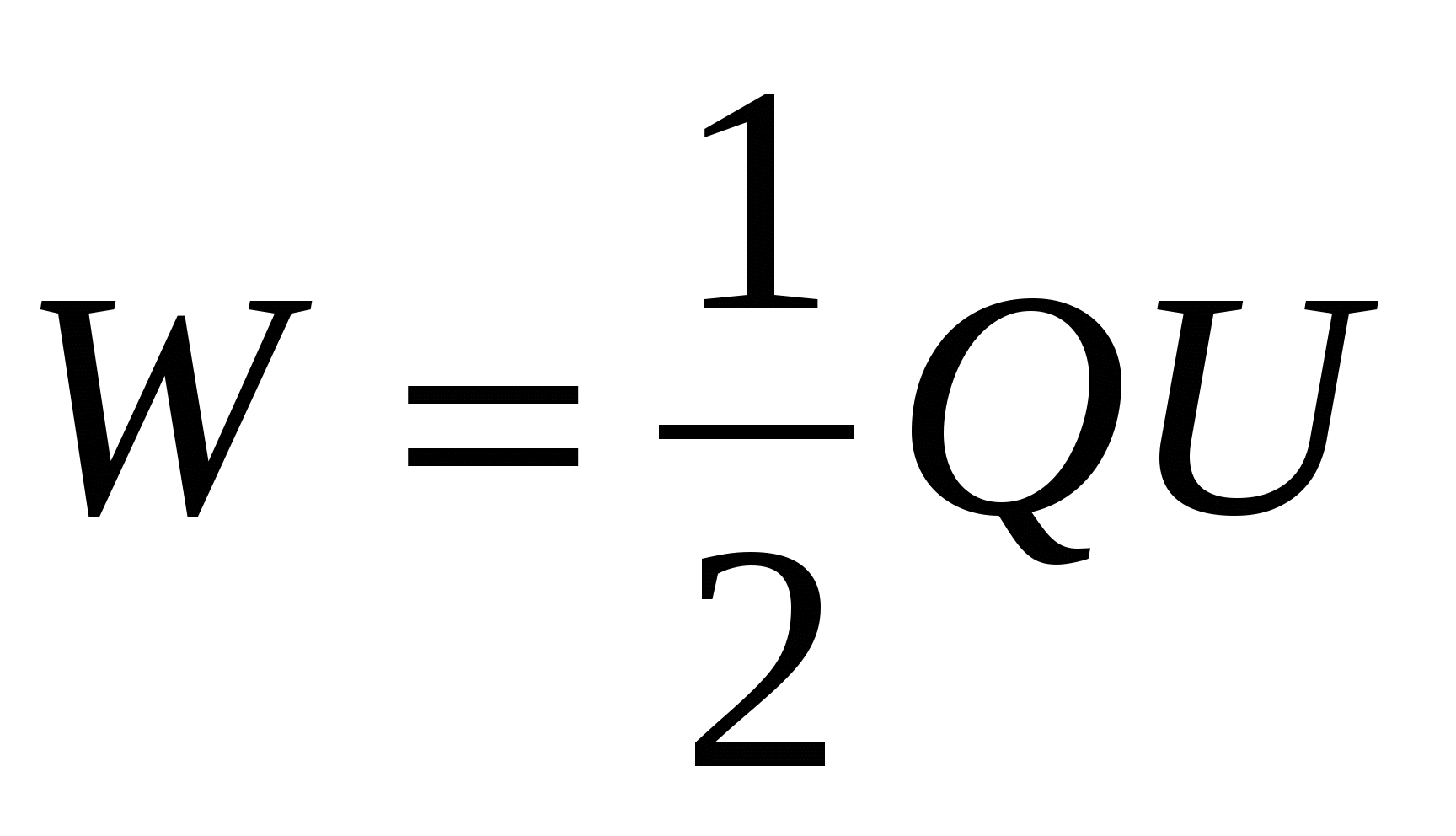 , , | (14.8) |
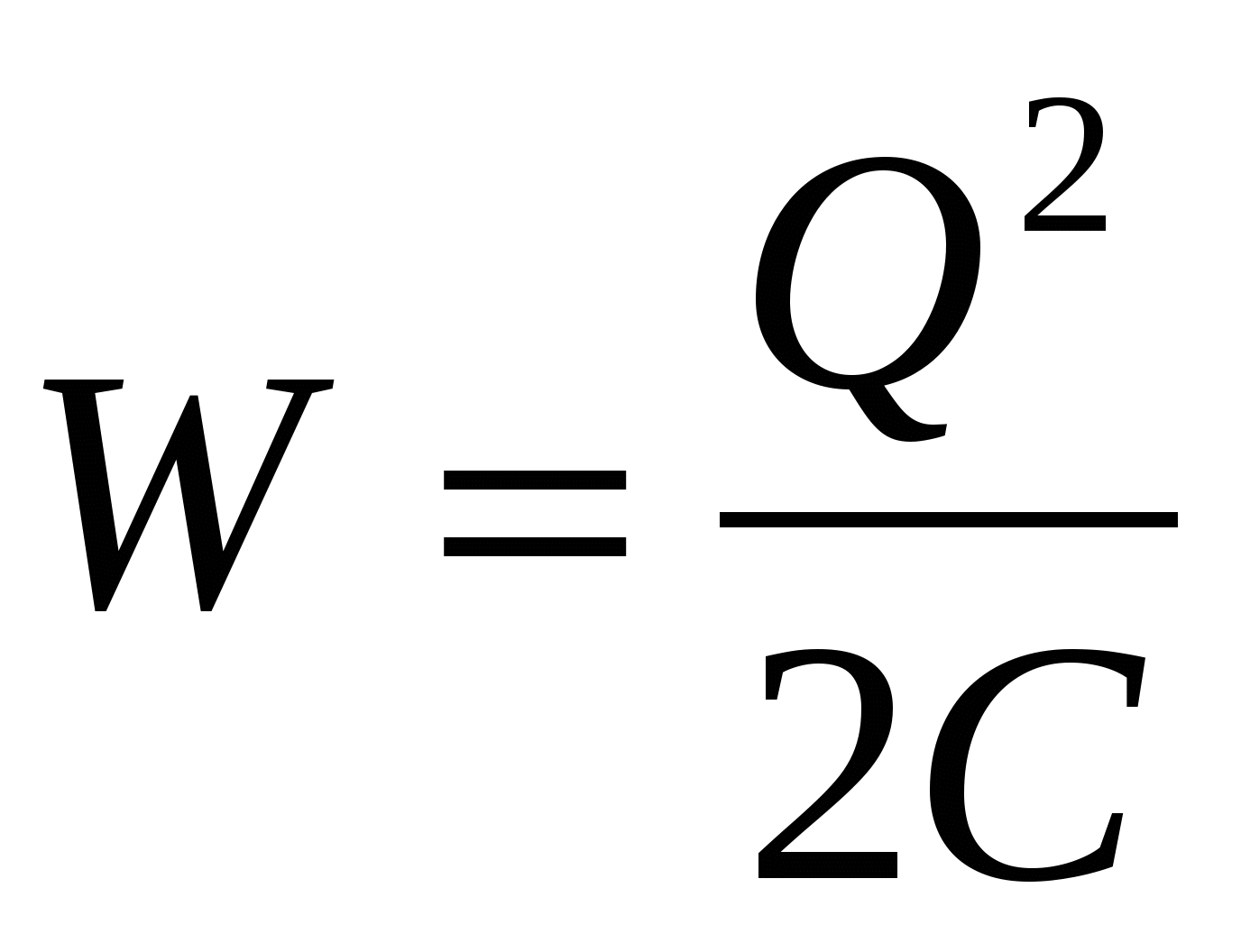 | (14.9) |
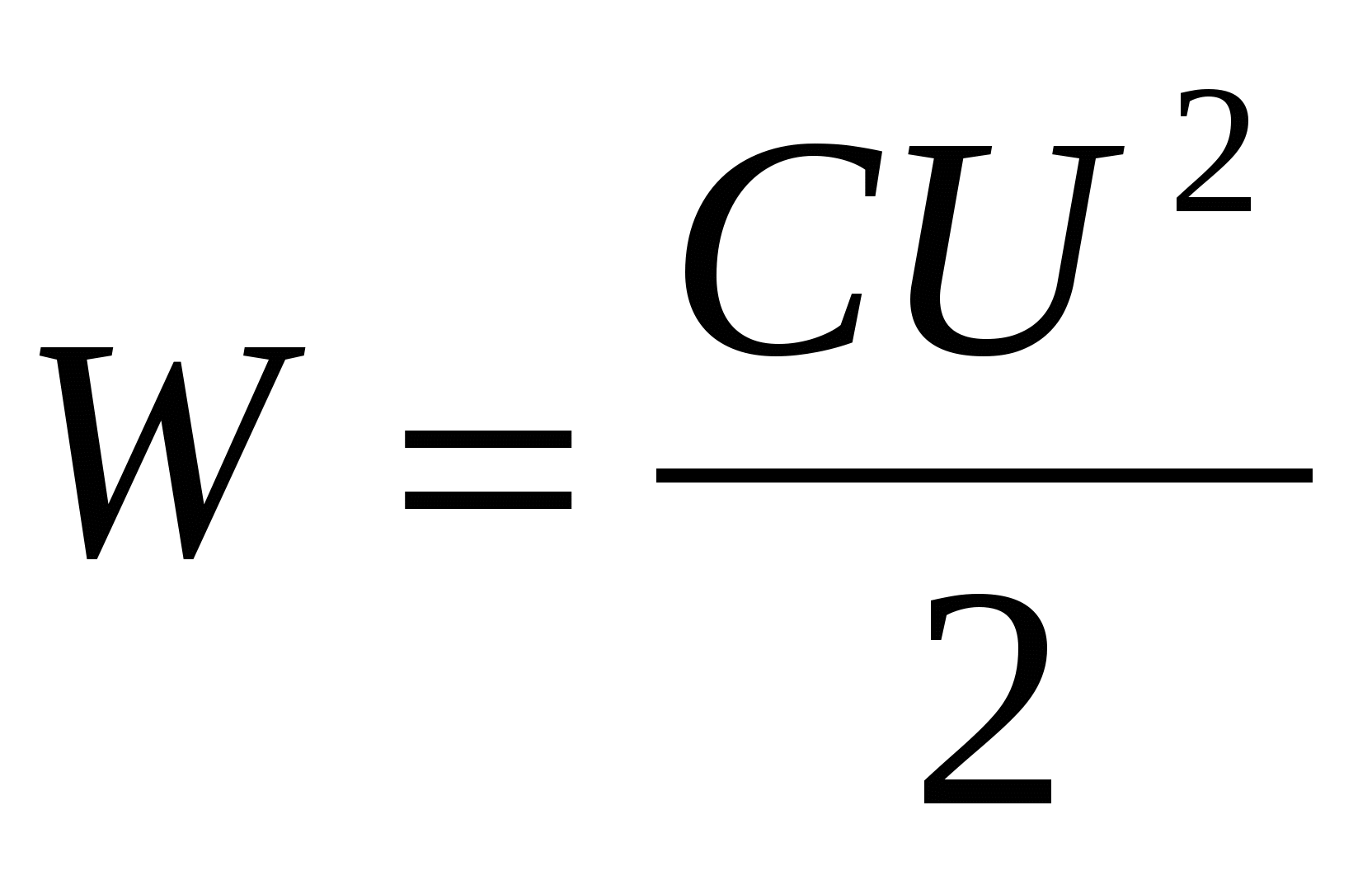 | (14.10) |
Vom efectua o analiză suplimentară pe baza formulei (14.9). Să ne imaginăm încărcarea condensatorului ca Q= S, unde este densitatea sarcinii de suprafață și S– zona plăcii condensatorului. Folosind în continuare expresia pentru capacitatea unui condensator plat (13.7), prezentăm (14.9) sub forma
În formula (14.9), energia unui condensator încărcat este exprimată în termeni de încărcare de pe plăcile sale și capacitatea. În formula (14.12), energia condensatorului este exprimată prin tensiune câmp electrostatic, concentrat între plăcile sale. În acest sens, se pune întrebarea fundamentală despre ceea ce servește ca purtător al energiei condensatorului: sarcini sau un câmp electrostatic. Această întrebare este esențială pentru dezbaterea de lungă durată dintre susținătorii acțiunii pe termen lung și scurt.
Susținătorii acțiunii pe distanță lungă au preferat formula (14.9), considerând-o ca energia potențială de interacțiune a două corpuri. Susținătorii acestei teorii au respins posibilitatea interacțiunii prin câmp.
Susținătorii teoriei cu rază scurtă de acțiune (teoria câmpului) credeau că energia condensatorului este energia câmpului electrostatic (formula (14.2)). Această energie este „împrăștiată” în întregul volum al condensatorului și, prin urmare, putem vorbi despre densitatea energiei volumetrice:
 [J/m3] sau
[J/m3] sau 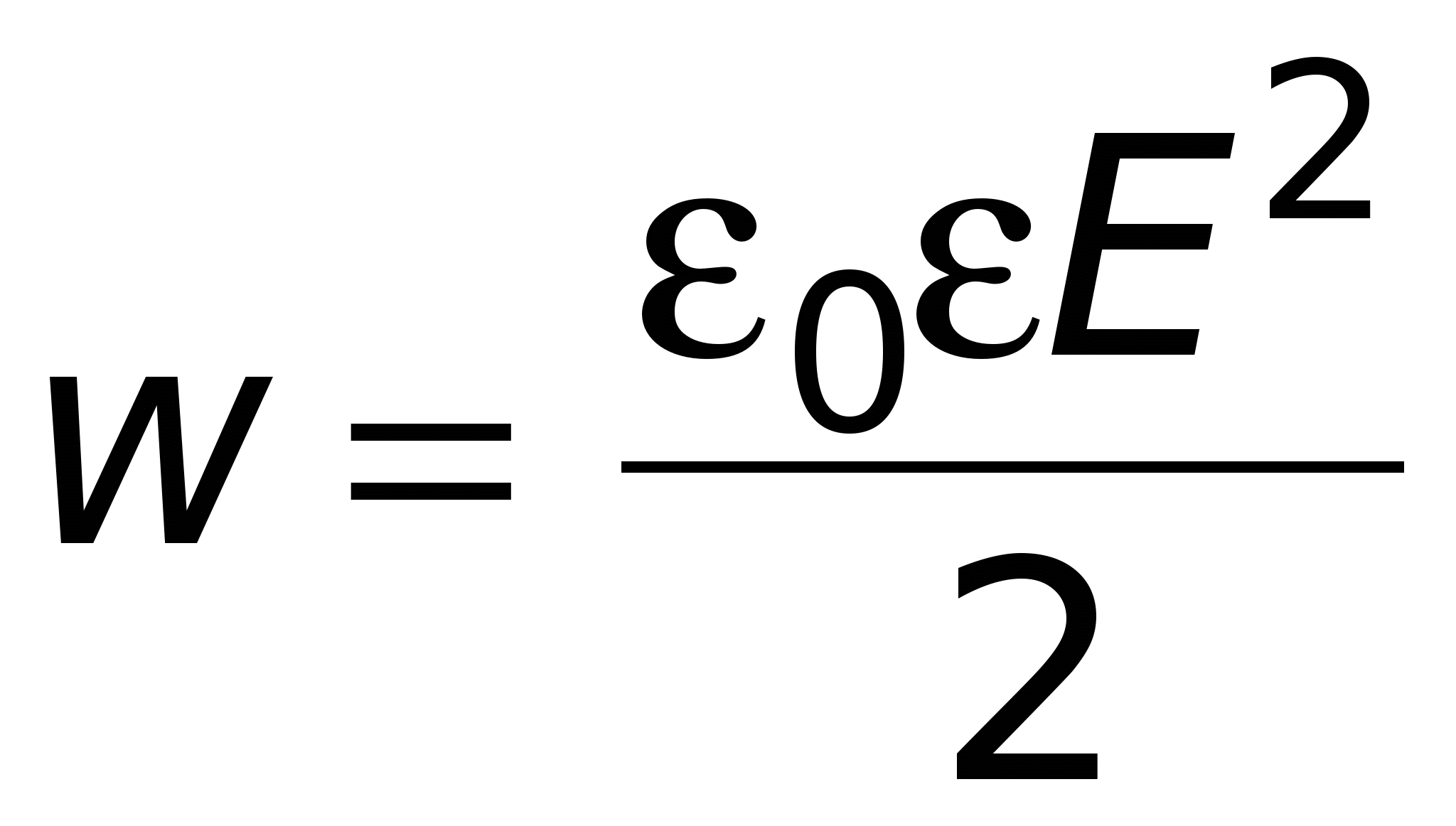 , Ținând cont de (12.11), formula (14.13) poate fi reprezentată sub forma
, Ținând cont de (12.11), formula (14.13) poate fi reprezentată sub forma
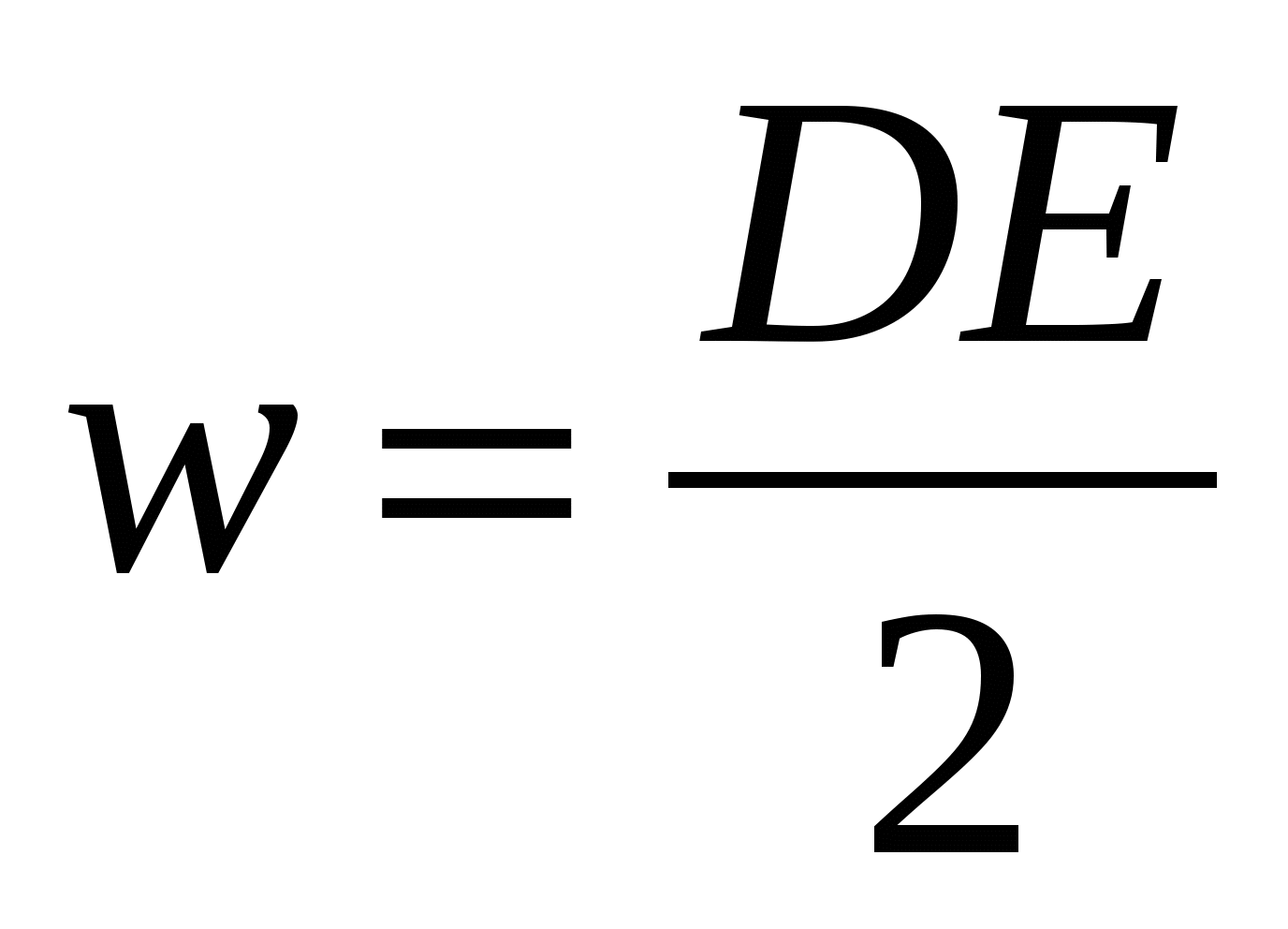 | (14.14) |
În cadrul electrostaticei, este imposibil să se rezolve întrebarea care este purtătorul de energie - sarcini sau un câmp, deoarece sarcinile staționare și câmpul electrostatic pe care le creează sunt inseparabile unele de altele. La studierea câmpurilor electrice și magnetice alternative, s-a dovedit că câmpul electromagnetic poate fi separat de sarcini, care există independent de acestea. Acesta este argumentul decisiv în favoarea teoriei acțiunii cu rază scurtă de acțiune (teoria câmpului).
Cursul 23.
15. Permanent electricitate
^
15.1. Forța și densitatea curentului
Curentul electric este mișcarea ordonată (dirijată) a microparticulelor încărcate sau a corpurilor macroscopice încărcate. Direcția curentului este considerată direcția de mișcare a sarcinilor pozitive; dacă curentul este creat de particule încărcate negativ (de exemplu, electroni), atunci direcția curentului este opusă direcției de mișcare a particulelor. Se face o distincție între curentul de conducție (mișcarea direcționată a particulelor încărcate în interiorul unui corp macroscopic) și curentul de convecție (mișcarea unui corp încărcat ca întreg). În cele ce urmează vom lua în considerare doar curentul de conducere.
Cantitativ, curentul electric este caracterizat de o mărime scalară: puterea curentului eu iar mărimea vectorială – densitatea curentului electric 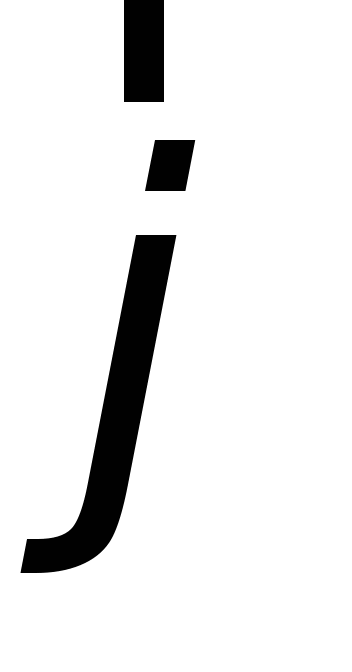 .
.
Puterea curentului este numeric egală cu sarcina care trece prin secțiunea transversală a conductorului pe unitatea de timp:
unde semnul „” indică faptul că site-ul 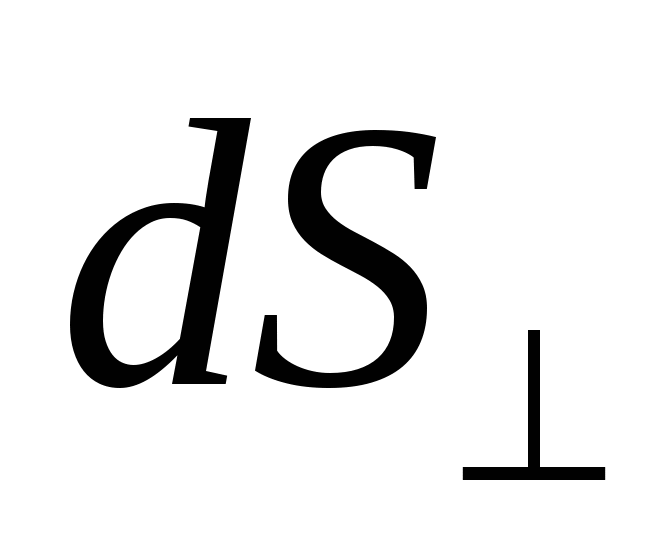 orientată perpendicular pe direcția curentului. Direcția vectorului coincide cu direcția de mișcare a sarcinilor pozitive.
orientată perpendicular pe direcția curentului. Direcția vectorului coincide cu direcția de mișcare a sarcinilor pozitive.
Să găsim o expresie pentru vectorul de densitate de curent în metale în care purtătorii de curent sunt electroni liberi. Sub influenta câmp electric electronii dintr-un metal se mișcă într-o direcție cu o viteză medie 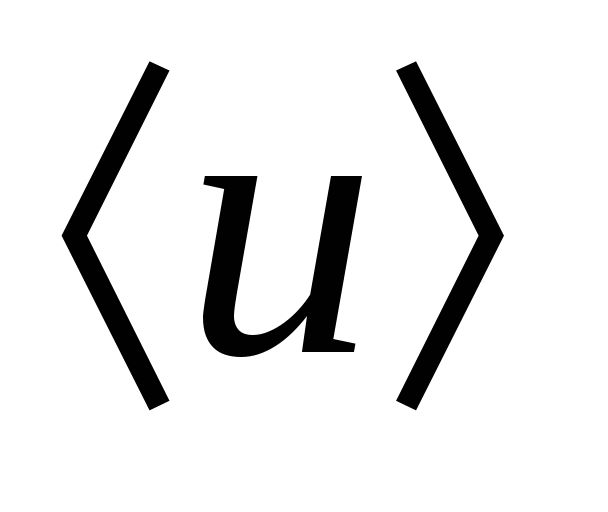 . Într-o unitate de timp, va trece printr-o unitate de secțiune transversală a unui conductor n electroni, unde n– numărul de electroni pe unitatea de volum (concentrație). Aceasta va transfera taxa ro. Prin urmare densitatea de curent
. Într-o unitate de timp, va trece printr-o unitate de secțiune transversală a unui conductor n electroni, unde n– numărul de electroni pe unitatea de volum (concentrație). Aceasta va transfera taxa ro. Prin urmare densitatea de curent
 . . | (15.3) |
15.2. Condiții de existență a curentului. Forțele exterioare. EMF
Dacă vectorul densității curentului nu se modifică în timp nici în mărime, nici în direcție, atunci un astfel de curent se numește constant. Să găsim condițiile de existență curent continuu.

Orez. 15.1
Să presupunem că la capetele conductorului se creează o diferență de potențial  , și
, și 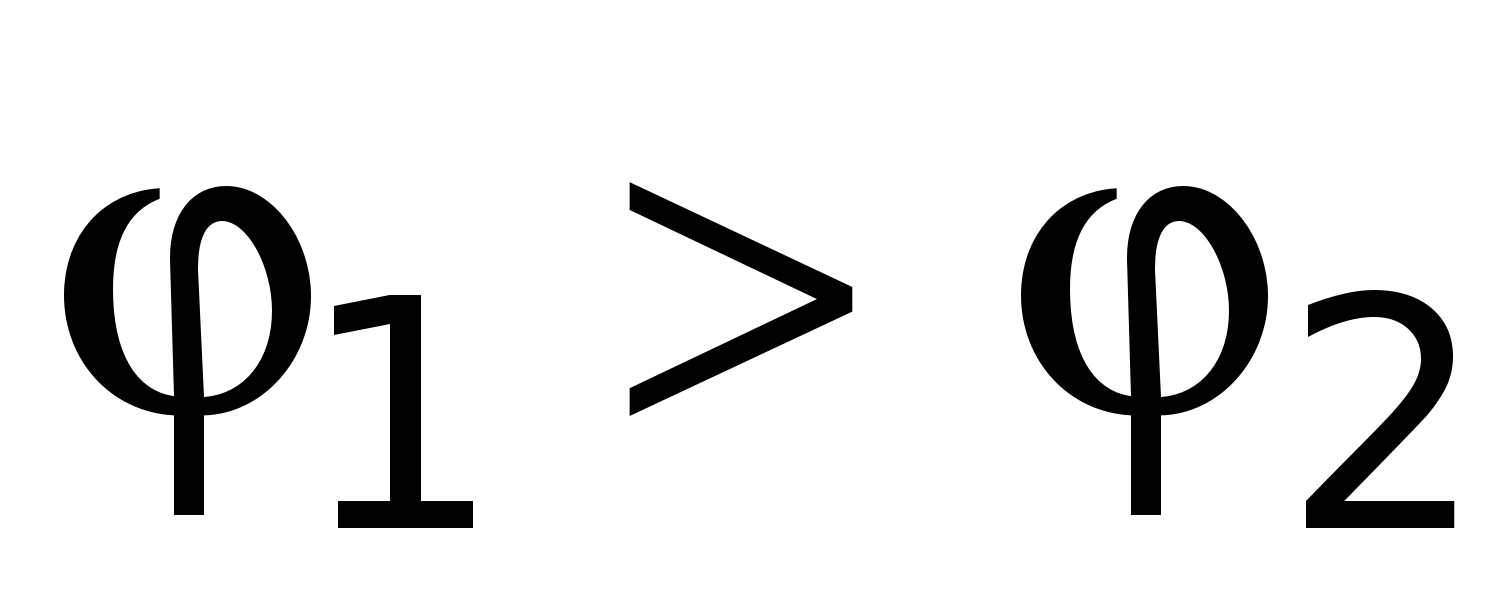 (Fig. 15.1). În acest caz, în conductor va apărea un curent de scurtă durată, cauzat de mișcarea ordonată a sarcinilor în direcția de scădere a potențialului (se presupune că purtătorii de curent au o sarcină pozitivă). Curentul va exista până când potențialele sunt egalizate la capetele conductorului.Pentru ca curentul să rămână constant pentru o lungă perioadă de timp, este necesar să îndepărtați sarcinile de la capătul conductorului cu un potențial mai mic până la capătul conductorului. conductor cu un potențial mai mare, adică efectuează circulația de încărcare. În acest sens, circuitul trebuie închis.
(Fig. 15.1). În acest caz, în conductor va apărea un curent de scurtă durată, cauzat de mișcarea ordonată a sarcinilor în direcția de scădere a potențialului (se presupune că purtătorii de curent au o sarcină pozitivă). Curentul va exista până când potențialele sunt egalizate la capetele conductorului.Pentru ca curentul să rămână constant pentru o lungă perioadă de timp, este necesar să îndepărtați sarcinile de la capătul conductorului cu un potențial mai mic până la capătul conductorului. conductor cu un potențial mai mare, adică efectuează circulația de încărcare. În acest sens, circuitul trebuie închis.
Forțele electrostatice nu pot asigura o astfel de circulație a sarcinilor, deoarece în secțiunea circuitului prezentată în Fig. 15.1 linie punctată, trebuie să lucrați împotriva câmpului electrostatic. Mișcarea sarcinilor în direcția creșterii potențialului este posibilă numai cu ajutorul unor forțe suplimentare de origine neelectrostatică, numite forțe externe. Aceste forțe pot fi furnizate de procese chimice (pile galvanice), câmpuri electrice turbioare (generatoare de curent alternativ sau de curent continuu), etc.
Spre deosebire de forțele electrostatice, munca efectuată de forțele externe pentru a muta o sarcină într-un cerc închis este diferită de zero. Forta electromotoare(EMF) este munca efectuată de forțele externe pentru a deplasa o singură sarcină pozitivă prin circuit, 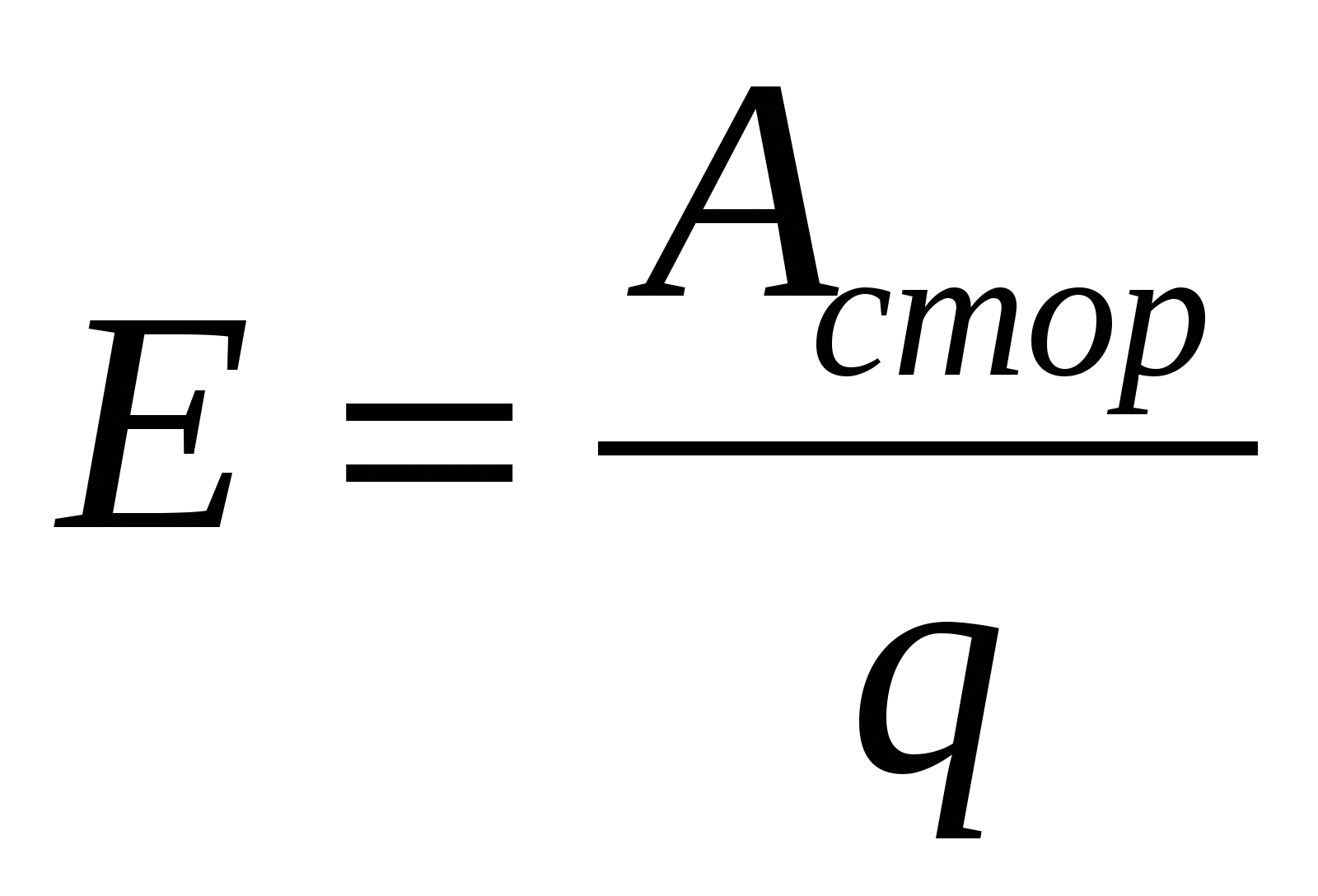 , (15.4) Ca și diferența de potențial, EMF se măsoară în volți.
, (15.4) Ca și diferența de potențial, EMF se măsoară în volți.
Să luăm în considerare o secțiune a circuitului în care, pe lângă forțele externe, acționează și forțele electrostatice. Atunci munca pentru a muta sarcina în această zonă va fi egală cu suma muncii: 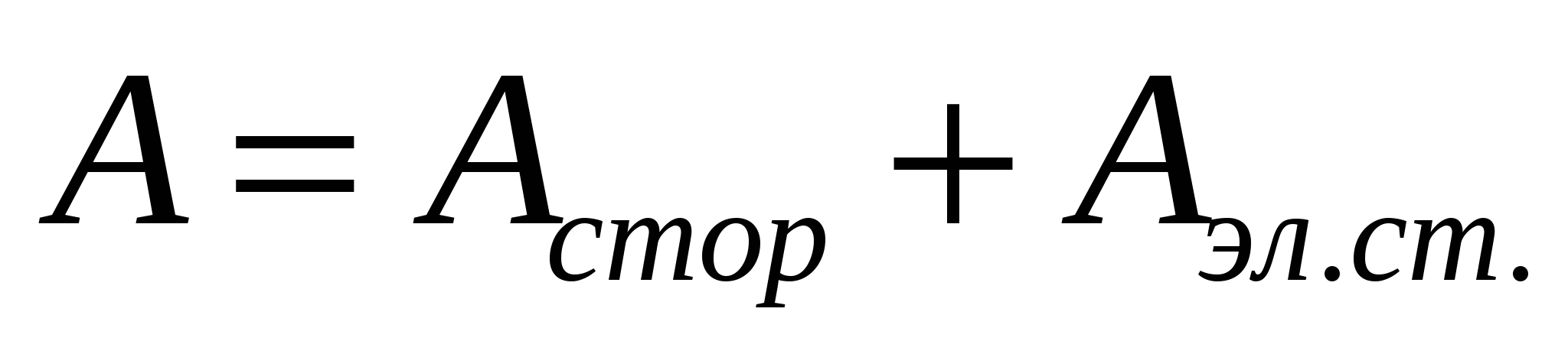
Să împărțim această expresie la taxă q:
Lucrul total efectuat de forțele externe și electrostatice pentru a deplasa o singură sarcină pozitivă într-o anumită secțiune a circuitului se numește tensiune sau cădere de tensiune:
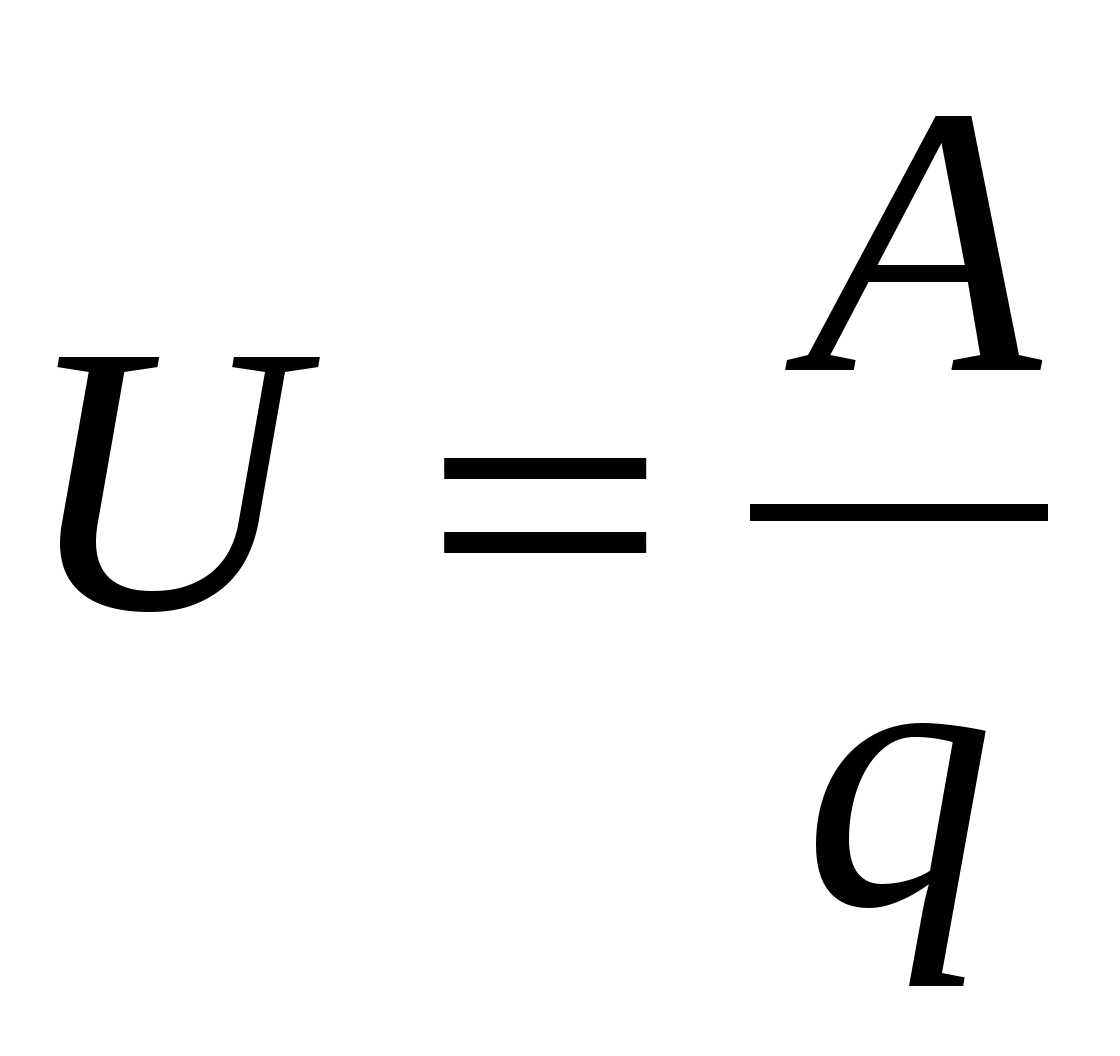 . . | (15.7) |
Înlocuind (15.4), (15.6) și (15.7) în (15.5), obținem relația dintre tensiune, fem și diferența de potențial U=E + ( 1 - 2 )
Din (15.8) este clar că tensiunea U egală cu suma algebrică a emf și diferența de potențial dintr-o secțiune dată a circuitului.
^
15.3. Legea lui Ohm
15.3.1. Legea lui Ohm pentru o secțiune neuniformă a unui circuit
Ohm a stabilit experimental că puterea curentului într-o anumită secțiune a circuitului este proporțională cu tensiunea și invers proporțională cu rezistența: 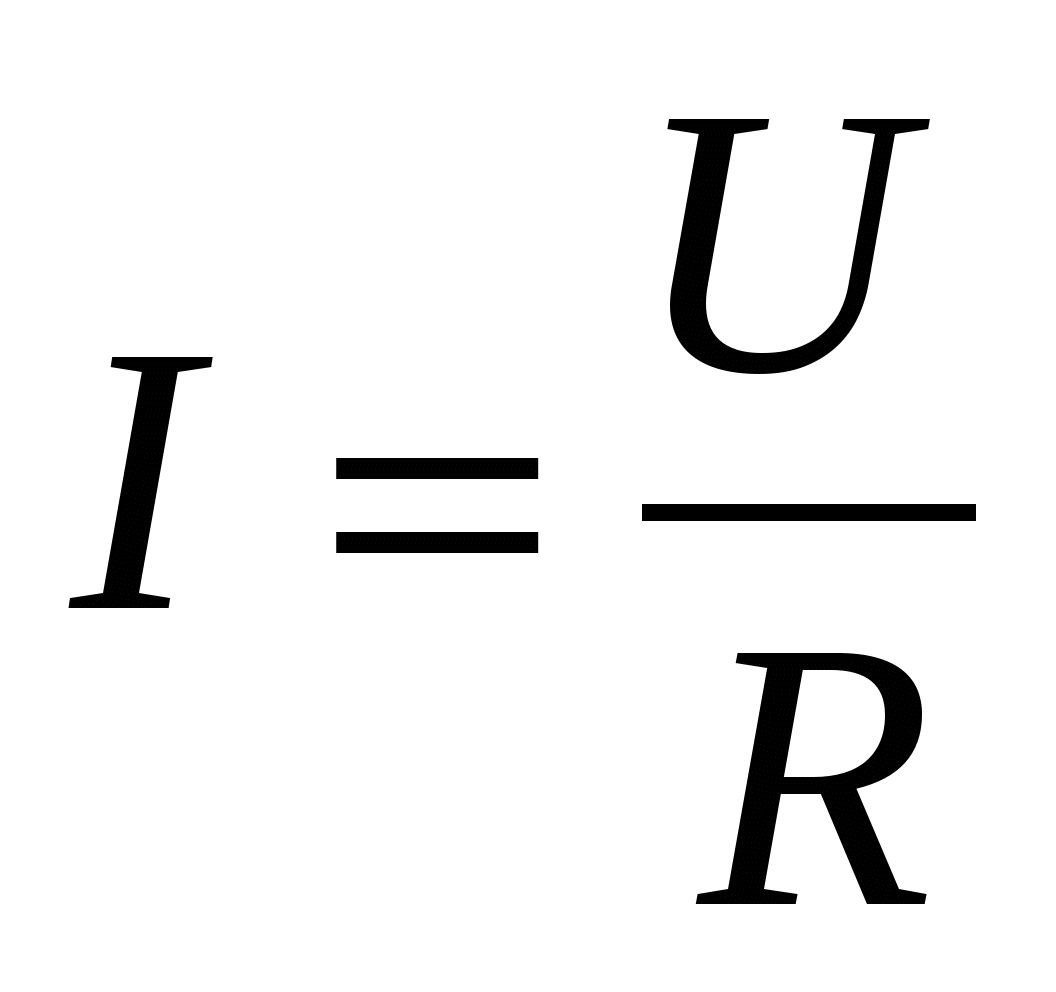 . . | (15.9) |
Să găsim din (15.9) tensiunea Uși înlocuiți în (15.8): IR= E +( 1 – 2 ) , (15.10)
Expresia rezultată este legea lui Ohm pentru o secțiune neuniformă a lanțului, i.e. secțiunea circuitului care conține EMF.

Orez. 15.2
La uz practic formula (15.10) trebuie să setați semnele pentru tensiune și fem. Pentru a face acest lucru, setăm în mod arbitrar direcția de ocolire (în Fig. 15.2, direcția de ocolire este aleasă în sensul acelor de ceasornic). Dacă direcția curentului coincide cu direcția de ocolire, atunci este luată cu semnul „+”, altfel trebuie luat cu semnul „-”. În fig. 15.2 direcția bypass-ului și direcția curentului nu coincid, deci în formula (15.10) IR ia-l cu semnul minus.
Restul buclei închise din fig. 15.2 este prezentat cu o linie punctată. EMF de circuit extern„Dispersează” încărcăturile din „plus” în „minus”. Trebuie luată cu semnul „+” dacă acționează în direcția de ocolire și cu semnul „–” în caz contrar. În conformitate cu aceasta, în diagrama prezentată în fig. 15.2, EMF trebuie luat cu semnul „+”. Astfel, în acest caz scriem legea lui Ohm pentru o secțiune neuniformă a lanțului sub forma: –
IR=
E
+(
1
–
2
)
.
^
15.3.2. Legea lui Ohm pentru un circuit complet
Când te plimbi lanț complet punctele de început și de sfârșit sunt aceleași, deci 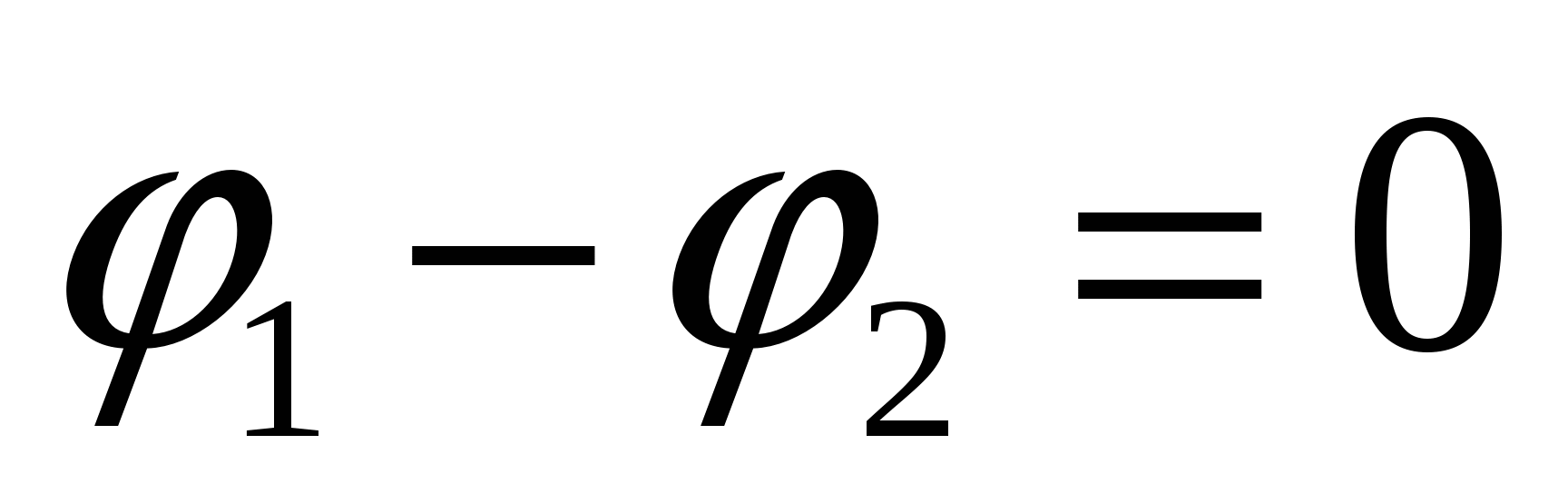 ;
;
^
15.3.3. Legea lui Ohm pentru o secțiune omogenă a unui lanț
O secțiune a circuitului care nu conține o sursă EMF se numește omogenă, adică în formula (15.10) trebuie să punem E
=0
. Apoi 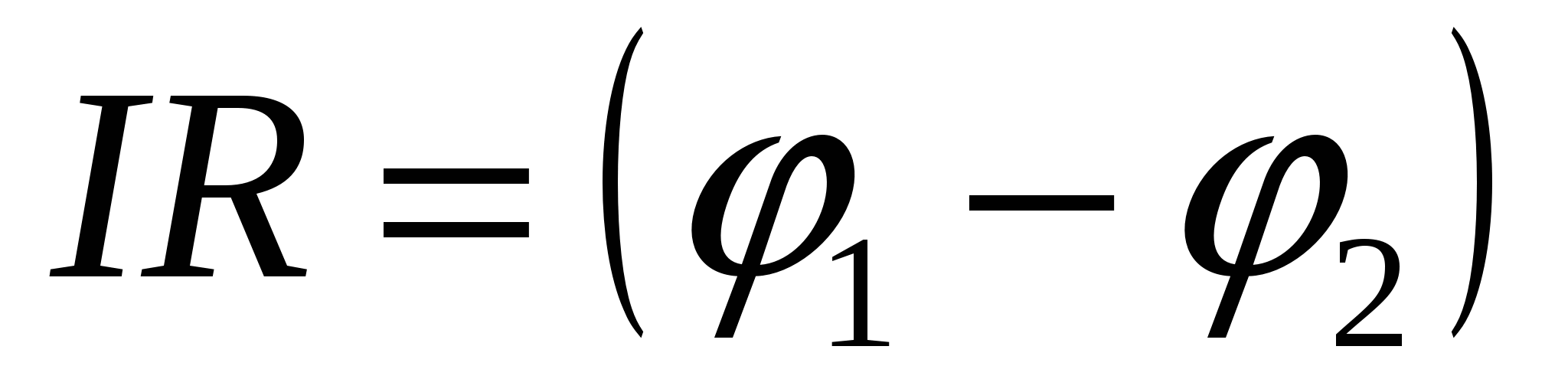 .
.
În acest caz, căderea de tensiune coincide cu diferența de potențial U= 1 - 1, adică.
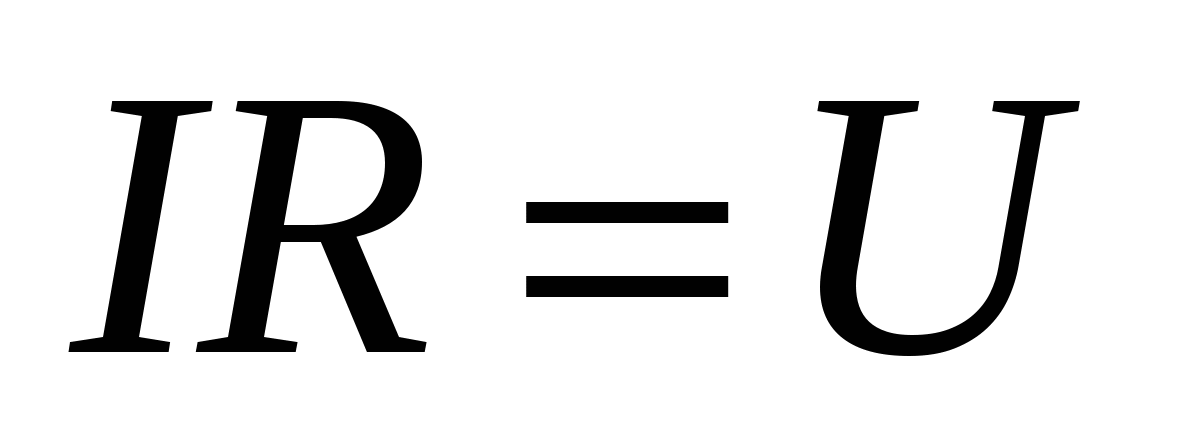 , , | (15.13) |
care coincide şi cu (15.9).
Formulele (15.9) și (15.13) reprezintă legea lui Ohm în formă integrală.
^
15.3.4. Legea lui Ohm în formă diferențială
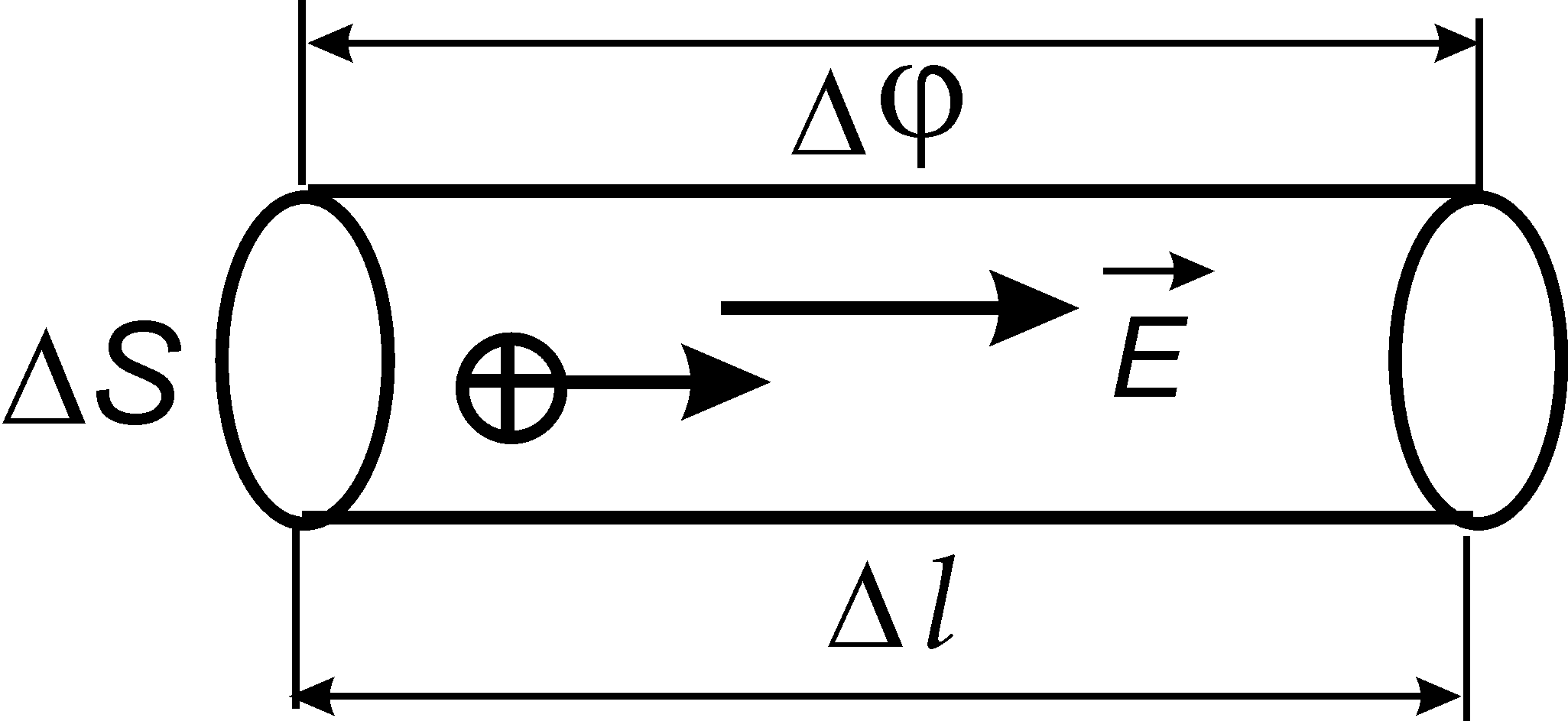
Orez. 5.3
Să alegem un cilindru elementar cu secțiune transversală în interiorul conductorului purtător de curent S iar lungimea l(Fig. 15.3). Puterea actuală în ea eu=S, și rezistența acestuia  , unde este rezistivitatea conductorului. Diferența de potențial la capetele cilindrului . Apoi scriem legea lui Ohm (vezi (15.9)) sub forma
, unde este rezistivitatea conductorului. Diferența de potențial la capetele cilindrului . Apoi scriem legea lui Ohm (vezi (15.9)) sub forma
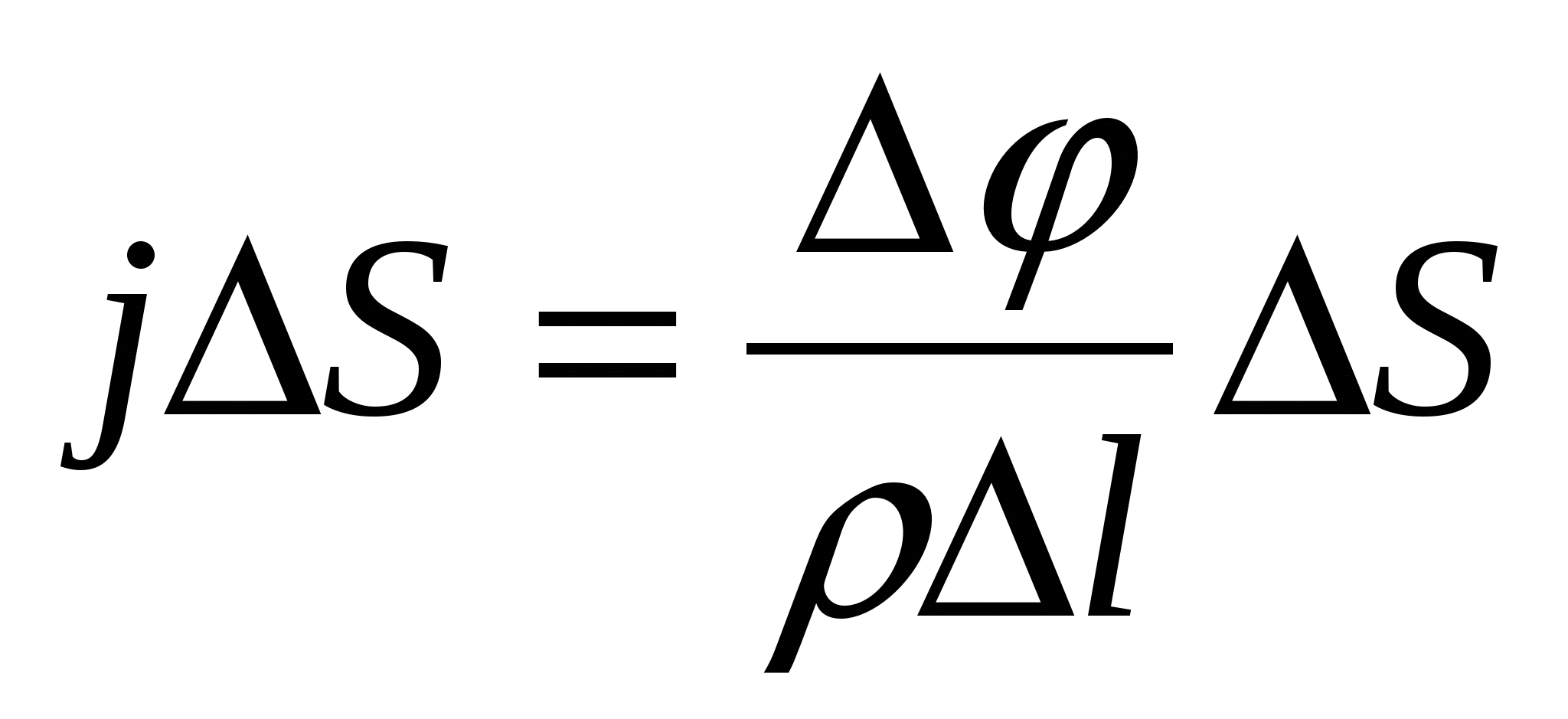 sau .
sau .
Ținând cont de (11.30), ultima expresie poate fi transformată în forma
 . . | (15.14) |
Reciproca rezistivității se numește conductivitate:
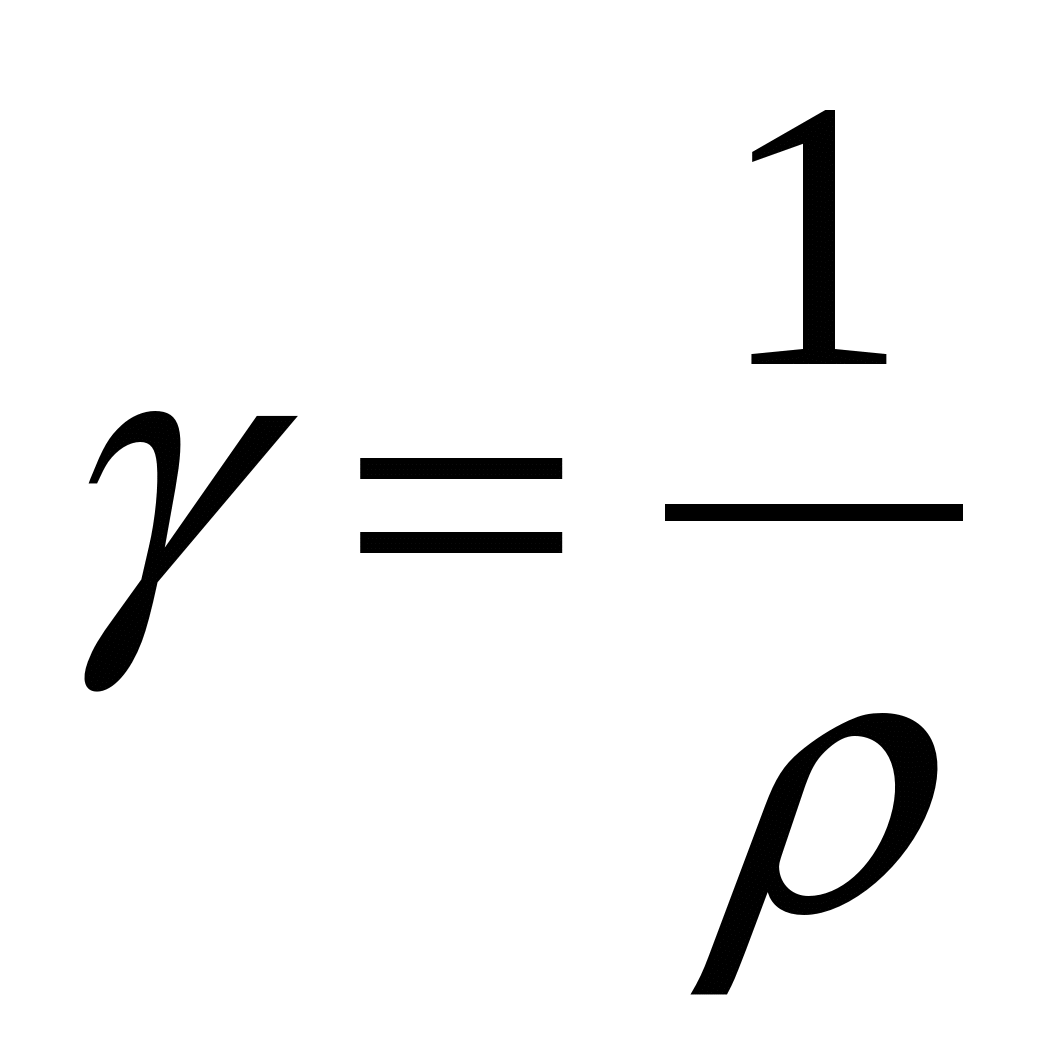 .
.Atunci legea lui Ohm în formă diferențială (15.4) poate fi dată sub forma 
^
15.4. Legea Joule-Lenz
15.4.1. Legea Joule-Lenz în formă integrală
Joule și, independent de el, Lenz au stabilit experimental o sută cantitatea de căldură eliberată într-un conductor prin rezistență R pe parcursul dt, proporțional cu pătratul curentului, rezistenței și timpului: 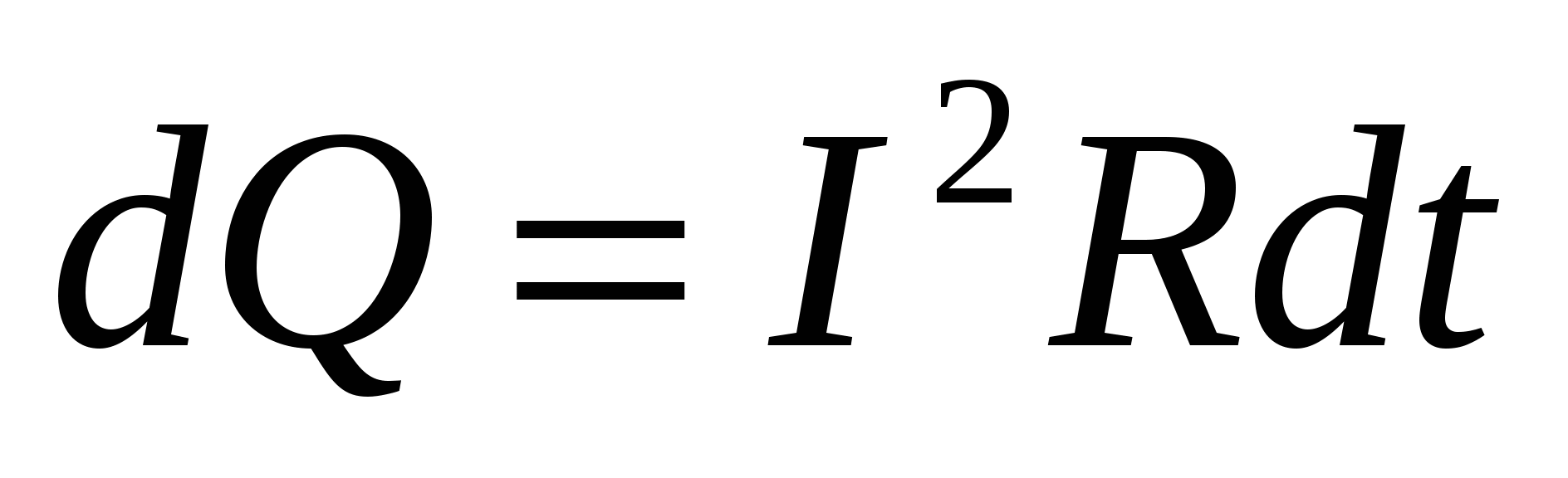 . . | (15.16) |
Formula (15.16) reprezintă legea Joule-Lenz în formă integrală.
^
15.4.2. Legea Joule-Lenz în formă diferențială
Să selectăm, ca mai înainte, un volum cilindric elementar în interiorul conductorului (Fig. 15.3). Să înlocuim în (15.16)
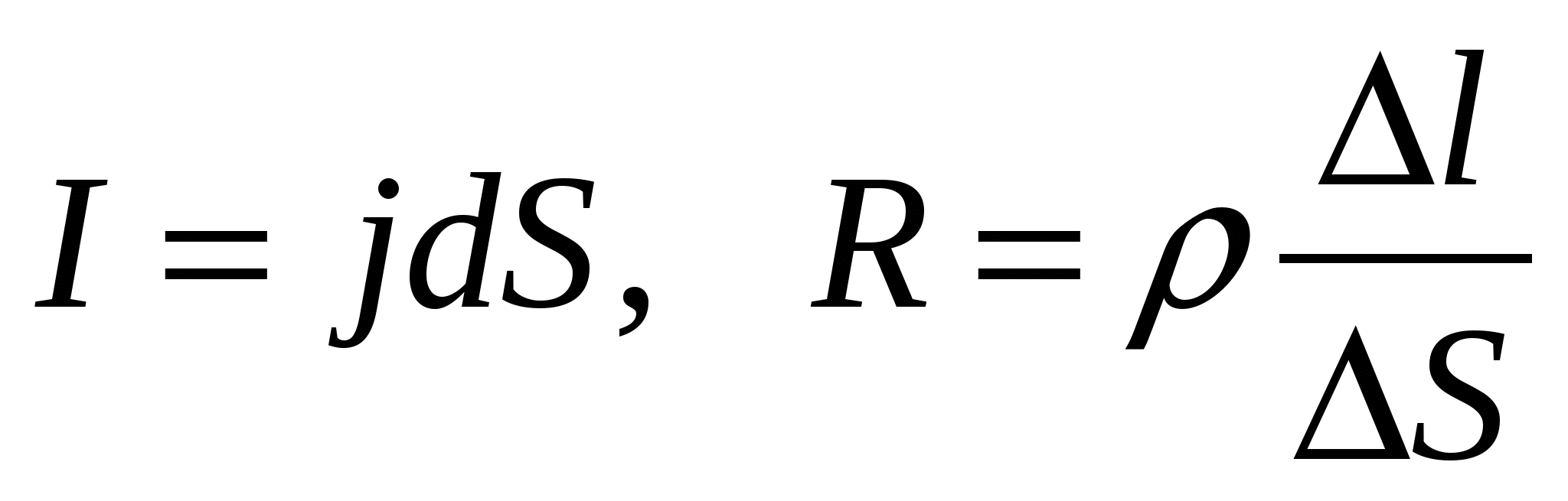 . Apoi
. Apoi  Unde V= lS– volumul conductorului. Să introducem puterea termică specifică
Unde V= lS– volumul conductorului. Să introducem puterea termică specifică 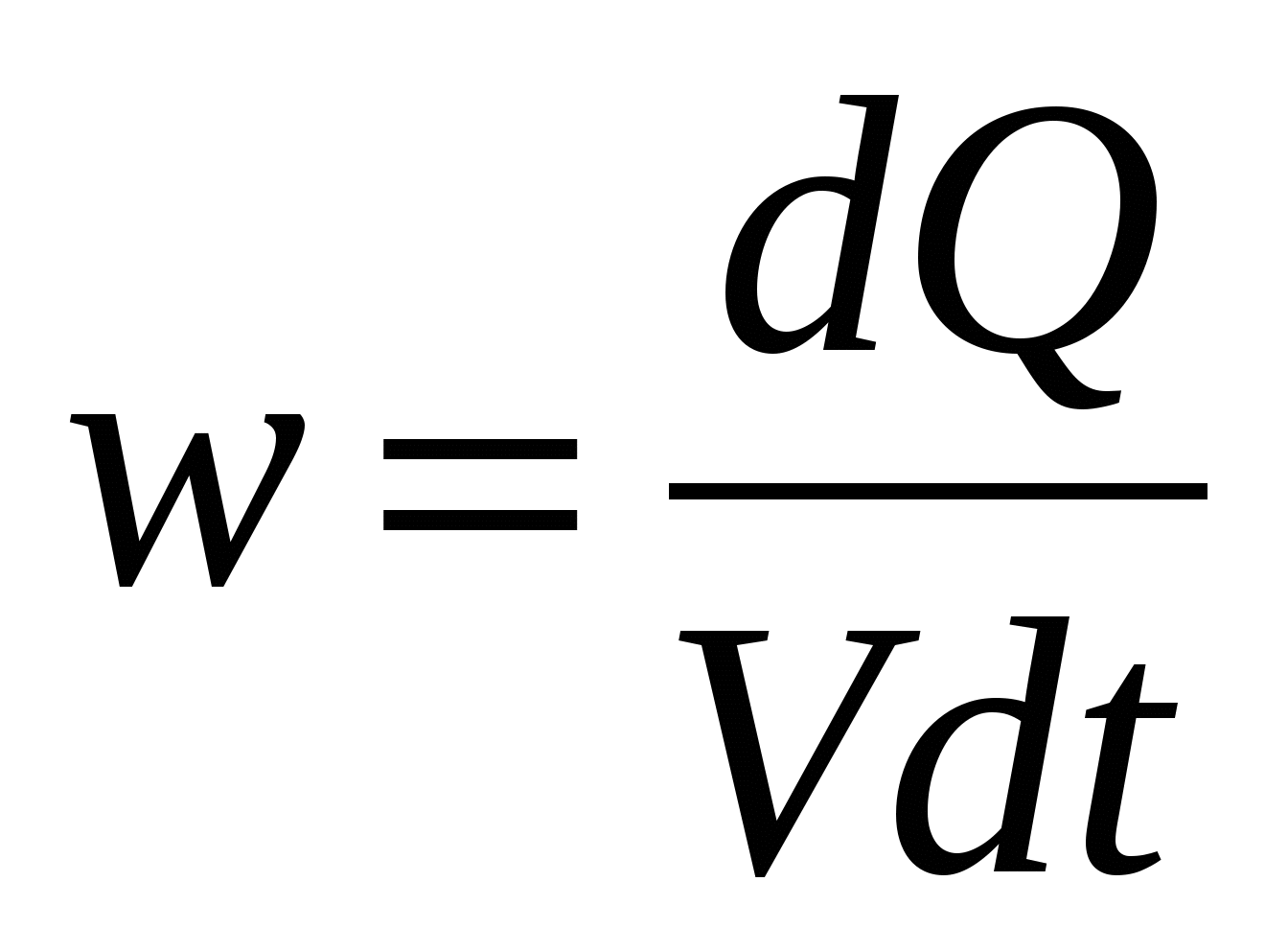 [J/m 3 s = W/m 3 ]. [J/m 3 s = W/m 3 ]. | (15.18) |
Puterea termică specifică este numeric egală cu cantitatea de căldură eliberată pe unitate de volum a conductorului pe unitatea de timp. Cu alte cuvinte, aceasta este puterea termică dezvoltată pe unitate de volum. Ținând cont de (15.18), expresiei (15.17) i se poate da forma
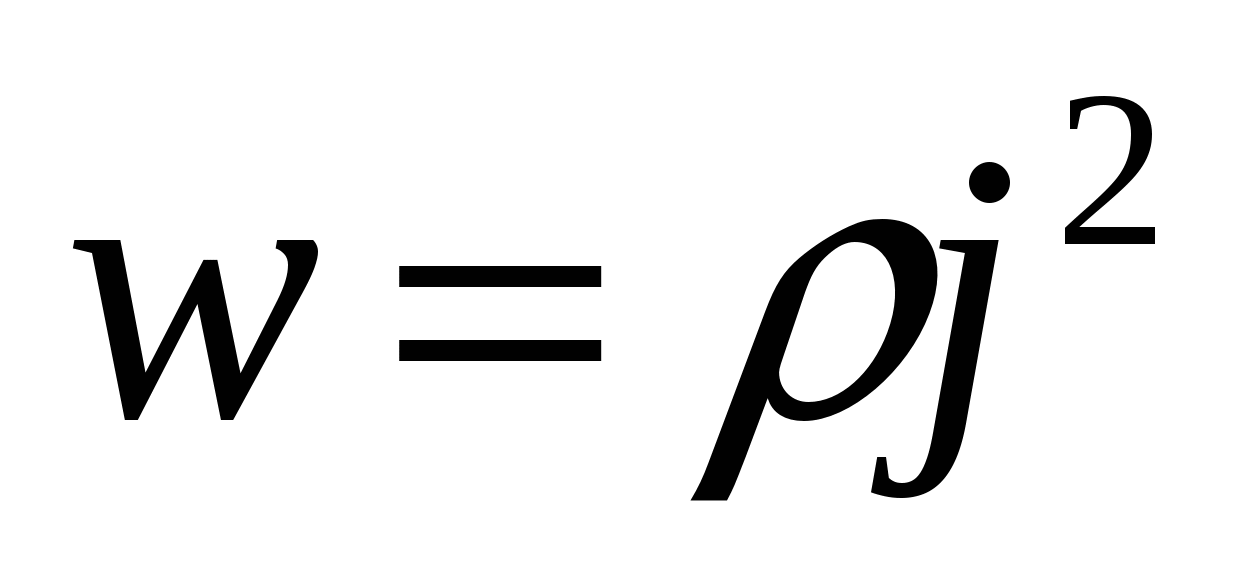 .
.
Formulele (15.19) și (15.20) reprezintă legea Joule-Lenz în formă diferențială.
Cursul 24.
^
15.5. Justificarea legilor lui Ohm și Joule-Lenz conform teoriei electronice clasice
În clasică teoria electronilor metale se acceptă următorul model.
1. Purtătorii de curent în metale sunt electronii liberi.
2. Electronii liberi formează un gaz de electroni, care este similar în proprietăți cu un gaz ideal. Există o singură diferență: atunci când electronii se mișcă, ei nu se ciocnesc între ei, ci cu ionii rețelei cristaline.
3. Sub influența unui câmp electric, electronii împreună cu mișcarea haotică cu viteza  începe să se deplaseze într-o direcție cu viteză
începe să se deplaseze într-o direcție cu viteză  . În acest caz, viteza mișcării direcționate este semnificativ mai mică decât viteza mișcării haotice
. În acest caz, viteza mișcării direcționate este semnificativ mai mică decât viteza mișcării haotice
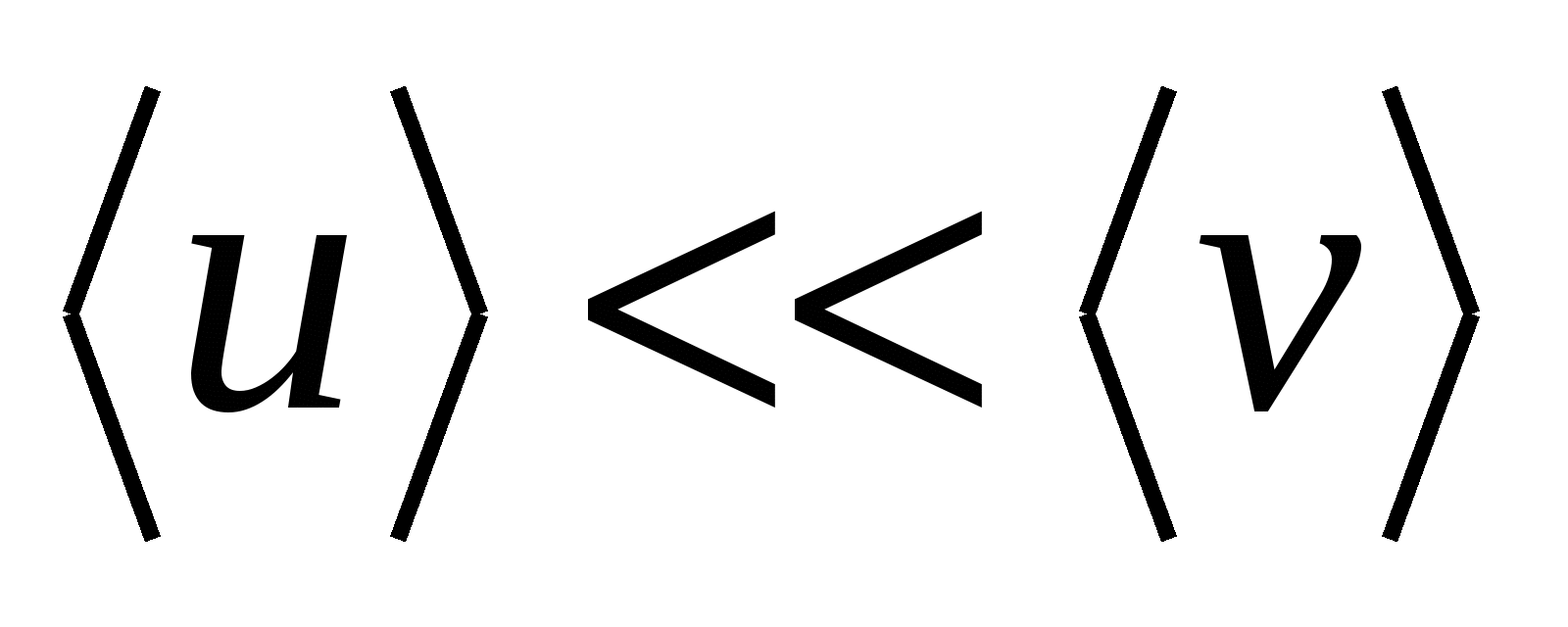 . . | (15.21) |
Să aflăm viteza mișcării direcționale a electronilor. Să presupunem că în momentul de față t= 0 viteza mișcării direcționale a electronilor u 0 =0. Sub forță F=eE electronul, în conformitate cu a doua lege a lui Newton, începe să se miște accelerat:
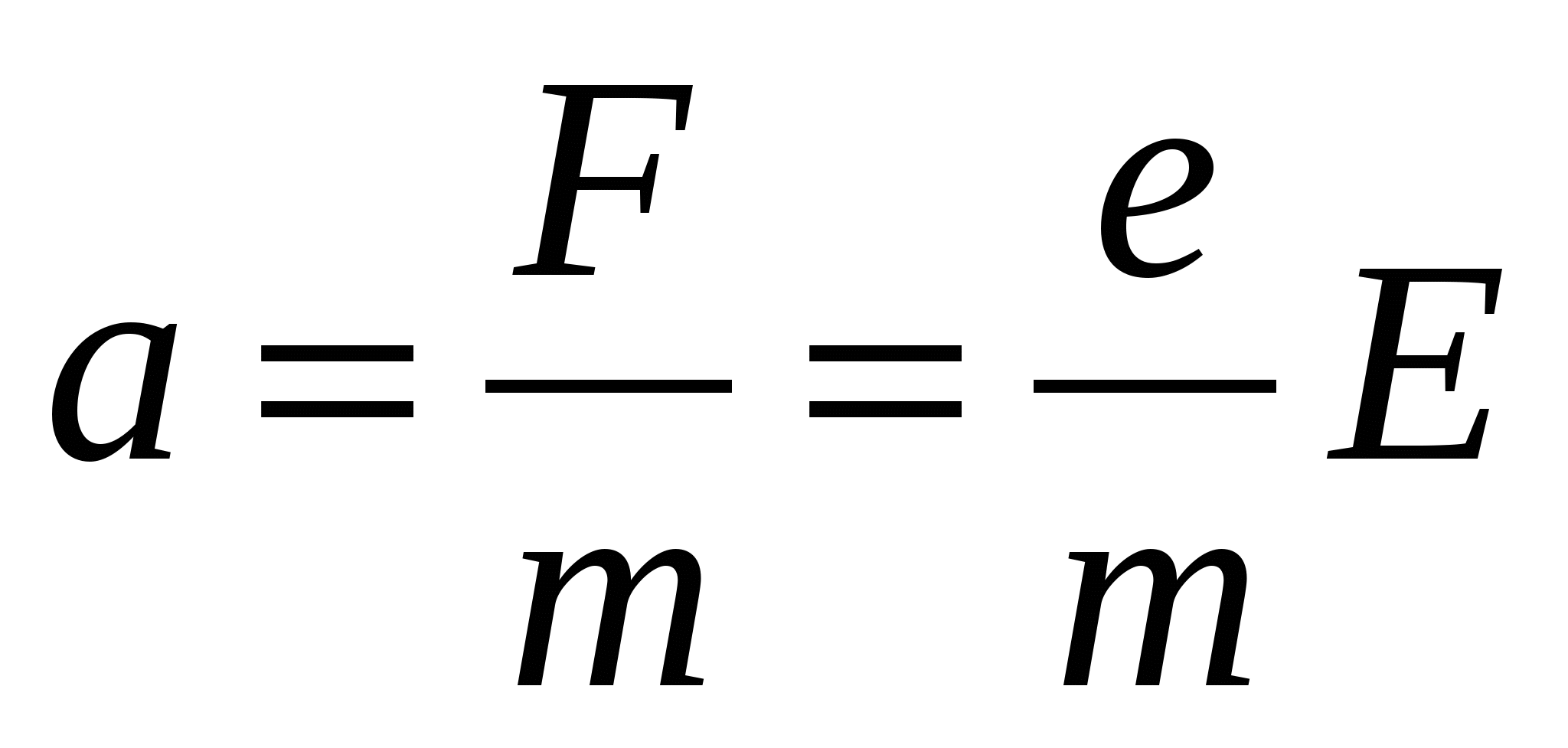 .
.
Viteza mișcării direcționale a electronului
 . . | (15.22) |

Orez. 15.4
Din formula (15.22) rezultă că viteza electronului u ar trebui să crească nelimitat în timp. Cu toate acestea, după o anumită perioadă de timp electronul experimentează o coliziune cu un ion al rețelei cristaline și se oprește. Dependența vitezei mișcării direcționale de timp este prezentată schematic în Fig. 15.4.
Timpul mediu dintre două ciocniri succesive de electroni
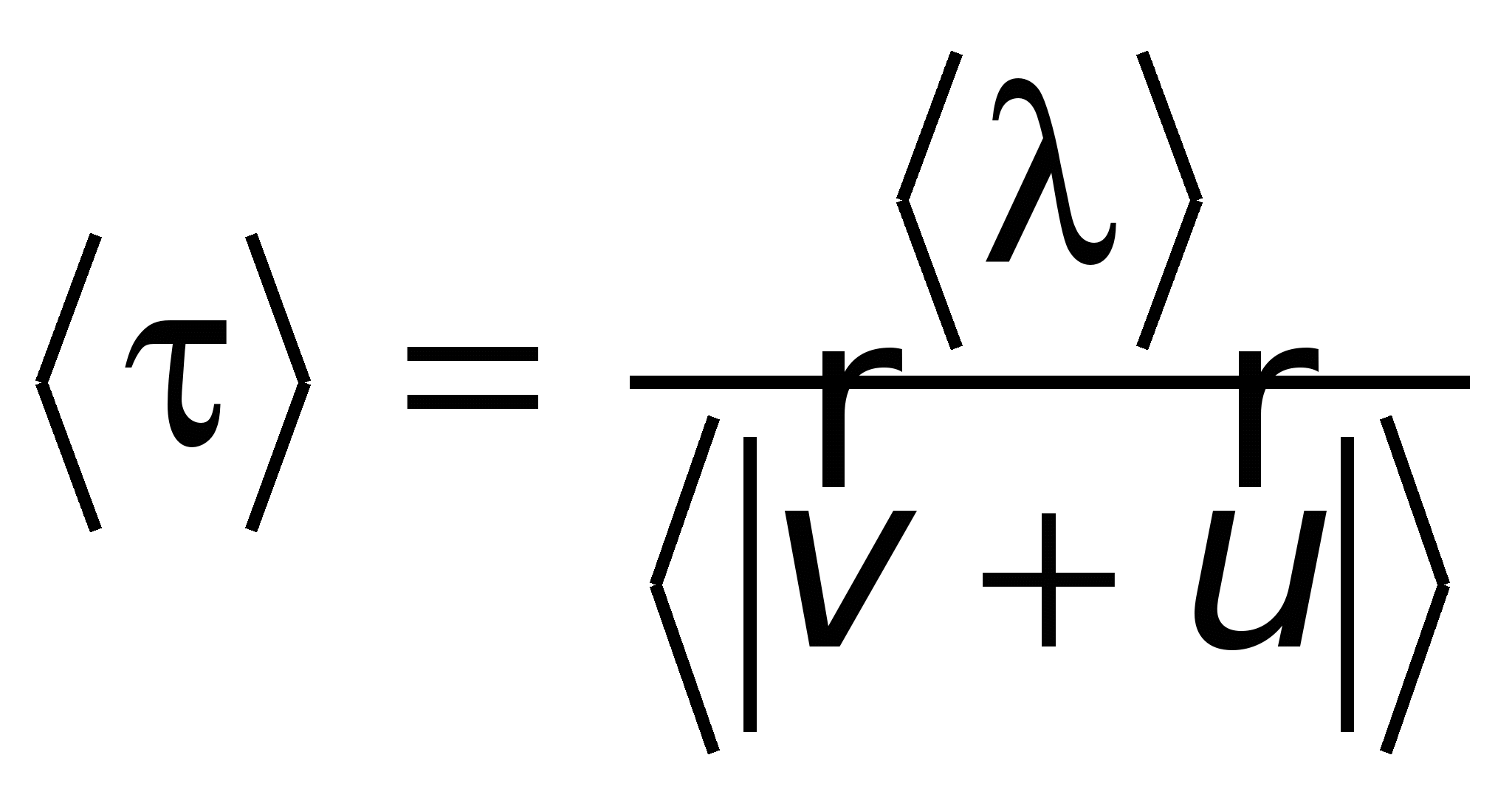 , , | (15.23) |
Unde
 – calea liberă medie a unui electron;
– calea liberă medie a unui electron;  – valoarea medie a vitezei sale, care este suma vectorială a vitezelor mișcărilor haotice și direcționale.
– valoarea medie a vitezei sale, care este suma vectorială a vitezelor mișcărilor haotice și direcționale. Din cauza inegalității (15.21), viteza mișcării direcționate poate fi neglijată, prin urmare
 . .
prin caracteristicile gazului de electroni. Pe baza conceptelor teoriei electronice clasice a metalelor, obținem acum legea Joule-Lenz. Până la sfârșitul căii libere, electronul are energie cinetică de mișcare direcționată
Înlocuind aici valoarea vitezei maxime de mișcare direcțională a electronului din (15.25) și ținând cont că numărul mediu de ciocniri în 1 s
obţinem legea Joule–Lenz
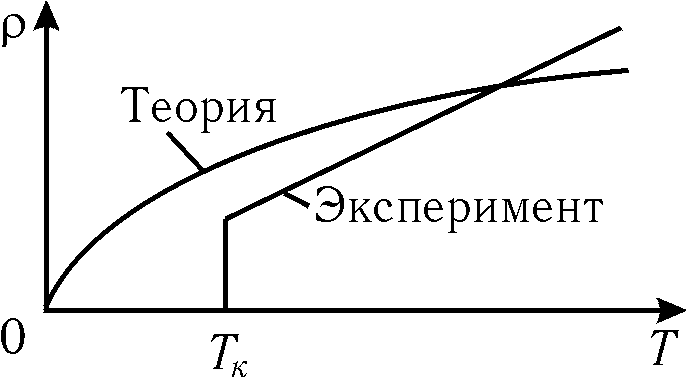
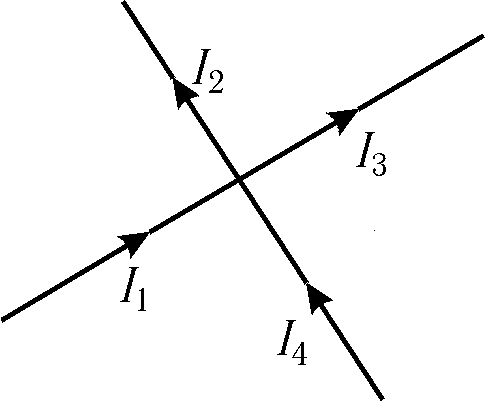
Dintr-o comparație a (15.30) și (15.20) găsim aceeași expresie pentru conductivitate termică, ca în legea lui Ohm (vezi (15.28)). În ciuda succeselor evidente ale teoriei electronice clasice a metalelor, aceasta a întâmpinat totuși o serie de dificultăți. În special, teoria clasică prezice incorect dependența rezistenței metalelor de temperatură. Analiza expresiei (15.29) arată că numai viteza mișcării haotice depinde de temperatură. În acest caz (vezi formula (8.18)) Orez. 15.5 Prima regulă a lui Kirchhoff. Suma algebrică a curenților care converg la un nod este egală cu zero, adică.
Un nod este un punct dintr-un circuit în care trei sau mai mulți conductori se intersectează. Curentul este luat cu semnul „+” dacă intră în nod; curentul care iese din nod este luat cu semnul „-”. Orez. 15.6 acestea. suma curenților care intră într-un nod este egală cu suma curenților care ies din acesta. Prima regulă a lui Kirchhoff este o consecință a legii conservării sarcinii electrice: sarcinile, odată ajunse într-un nod, nu dispar și nu se acumulează nicăieri. ^
A doua regulă a lui Kirchhoff.
Suma algebrică a căderilor de tensiune într-o buclă închisă, izolată dintr-un circuit complex, este egală cu suma algebrică a emfs incluse în această buclă:
Căderea de tensiune este luată cu semnul „+” dacă curentul este direcționat către ocolirea circuitului, iar „-” în caz contrar. EMF este luat cu semnul „+” dacă acționează în direcția de ocolire, iar „-” în caz contrar. Direcția de ocolire este aleasă în mod arbitrar. Pentru claritate, alegem direcția de traversare în sensul acelor de ceasornic. Să notăm, de exemplu, a doua regulă a lui Kirchhoff pentru contururi ^ ABCFAȘi ABCDEFA(Fig. 15.7): circuit ABCFA: eu 1 R 1 +eu 2 R 2 = E 1 – E 2 ; Circuit ABCDEFA: eu 1 R 1 -eu 3 R 3 = E 1 – E 3 . În cazul general, când circuitul are n noduri și m contururi, trebuie să faci n-1 ecuație conform primei reguli a lui Kirchhoff și m-1 ecuație conform celei de-a doua reguli. 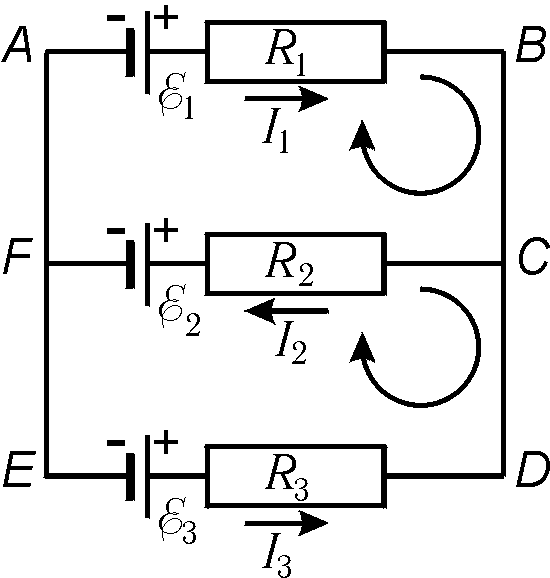 Orez. 15.7 Cursul 25. |
1. Energia unui sistem de sarcini punctuale staționare. Forțele de interacțiune electrostatică sunt conservatoare; prin urmare, sistemul de sarcini are energie potențială. Să găsim energia potențială a unui sistem de două sarcini punctuale staționare și situate la o distanță r una de cealaltă. Fiecare dintre aceste sarcini în câmpul celeilalte are energie potențială:
, ![]() ,
,
unde si sunt, respectiv, potentialele create de sarcina in punctul in care se afla sarcina si de sarcina in punctul in care se afla sarcina. Conform formulei (8.3.6),
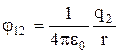 Și
Și 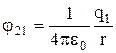 ,
,
![]()
Adăugând sarcini , , … la un sistem de două sarcini succesive, se poate verifica că în cazul n sarcini staționare, energia de interacțiune a sistemului de sarcini punctiforme este egală cu
 , (8.12.1.)
, (8.12.1.)
unde este potențialul creat în punctul în care sarcina este localizată de toate sarcinile, cu excepția celei i-a.
2. Energia unui conductor solitar încărcat. Să existe un conductor solitar a cărui sarcină, capacitate și potențial sunt, respectiv, egale cu q, C, . Să creștem sarcina acestui conductor cu dq. Pentru a face acest lucru, este necesar să transferați sarcina dq de la infinit la un conductor izolat, cheltuind munca egală cu
![]() .
.
Pentru a încărca un corp de la potențial zero la , trebuie să se lucreze
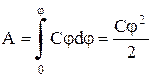 . (8.12.2.)
. (8.12.2.)
Energia unui conductor încărcat este egală cu munca care trebuie făcută pentru a încărca acest conductor:
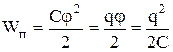 . (8.12.3.)
. (8.12.3.)
Formula (8.12.3.) se poate obține și din faptul că potențialul conductorului în toate punctele sale este același, deoarece suprafața conductorului este echipotențială. Presupunând potenţialul conductorului egal cu , din (8.12.1.) găsim
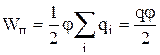 ,
,
unde este sarcina conductorului.
3. Energia unui condensator încărcat. Ca orice conductor încărcat, un condensator are energie, care, conform formulei (8.12.3.), este egală cu
 , (8.12.4.)
, (8.12.4.)
unde q este sarcina condensatorului, C este capacitatea acestuia și este diferența de potențial dintre plăci.
4. Energia câmpului electrostatic. Să transformăm formula (8.12.4.), care exprimă energia unui condensator plat prin sarcini și potențiale, folosind expresia pentru capacitatea unui condensator plat și diferența de potențial dintre plăcile sale (). Apoi primim
 , (8.12.5.)
, (8.12.5.)
unde V=Sd este volumul condensatorului. Formula (8.12.5.) arată că energia condensatorului este exprimată printr-o mărime care caracterizează câmpul electrostatic - tensiune E.
Formulele (8.12.4.) și respectiv (8.12.5.) relaționează energia condensatorului cu taxa pe coperțile sale și cu puterea câmpului. Desigur, se pune problema localizării energie electrostaticăși care este transportatorul său - taxe sau câmp? Răspunsul la această întrebare poate fi dat doar de experiență. Electrostatica studiază câmpurile constante în timp ale sarcinilor staționare, de ex. în ea câmpurile şi sarcinile care le determină sunt inseparabile unele de altele. Prin urmare, electrostatica nu poate răspunde la întrebările puse. Dezvoltarea ulterioară a teoriei și experimentului a arătat că variabile în timp electrice și campuri magnetice pot exista separat, indiferent de sarcinile care i-au excitat, și se răspândesc în spațiu sub formă undele electromagnetice, capabil transfera energie. Acest lucru confirmă în mod convingător punctul principal teoria cu rază scurtă a localizării energiei într-un câmpŞi ce dacă purtător energia este camp.
Densitate în vrac energie câmp electrostatic (energie pe unitate de volum)
 . (8.12.6.)
. (8.12.6.)
Expresia (8.12.6.) este valabilă numai pentru dielectric izotrop, pentru care este valabilă următoarea relaţie: .
Energia electrică a unui condensator cu plăci paralele poate fi exprimată în termeni de intensitatea câmpului dintre plăcile sale:
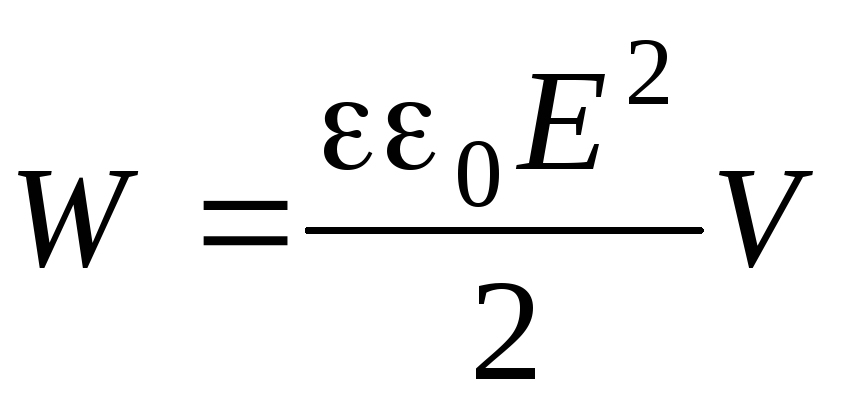 ,
,
Unde - volumul de spațiu ocupat de câmp, S– zona acoperirilor, d– distanța dintre ele. Se dovedește că tensiunea poate fi exprimată energie electricași un sistem arbitrar de conductori încărcați și dielectrici:
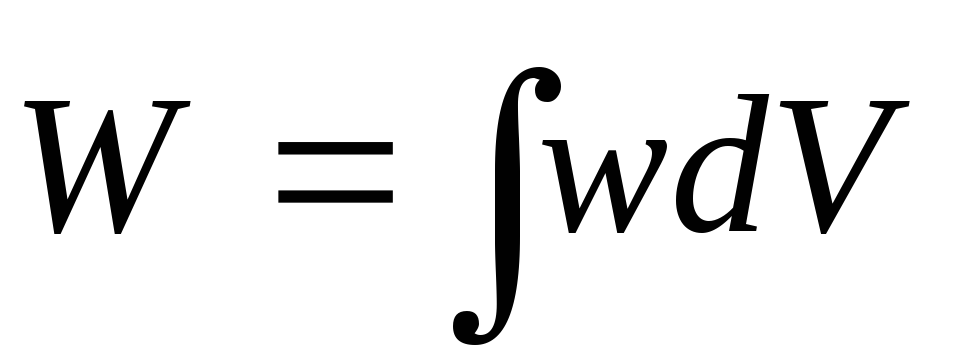 ,
(5)
,
(5)
 ,
,
iar integrarea se realizează pe întreg spațiul ocupat de câmp (se presupune că dielectricul este izotrop și 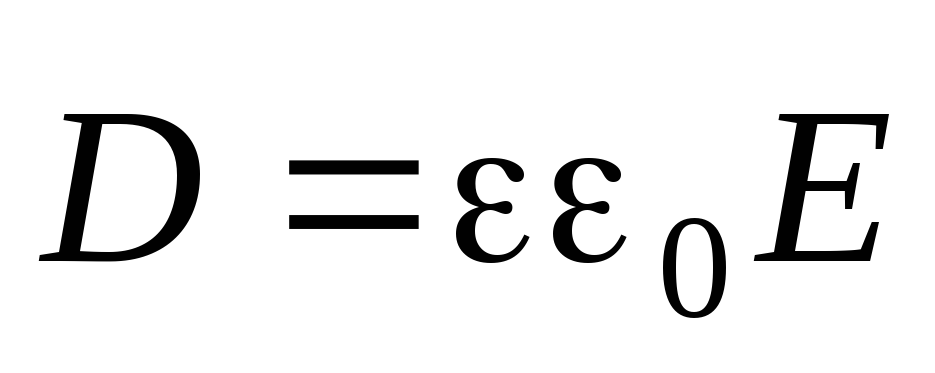 ). Magnitudinea w reprezintă energia electrică pe unitatea de volum. Forma formulei (5) dă motive să presupunem că energia electrică este conținută nu în sarcinile care interacționează, ci în spațiul lor de umplere a câmpului electric. În cadrul electrostaticei, această ipoteză nu poate fi verificată experimental sau fundamentată teoretic, dar luarea în considerare a câmpurilor electrice și magnetice alternative face posibilă verificarea corectitudinii interpretării acestui câmp a formulei (5).
). Magnitudinea w reprezintă energia electrică pe unitatea de volum. Forma formulei (5) dă motive să presupunem că energia electrică este conținută nu în sarcinile care interacționează, ci în spațiul lor de umplere a câmpului electric. În cadrul electrostaticei, această ipoteză nu poate fi verificată experimental sau fundamentată teoretic, dar luarea în considerare a câmpurilor electrice și magnetice alternative face posibilă verificarea corectitudinii interpretării acestui câmp a formulei (5).
7. Energia câmpului electric (Exemple de rezolvare a problemelor) Energia de interacțiune a sarcinii
Exemplul 1.
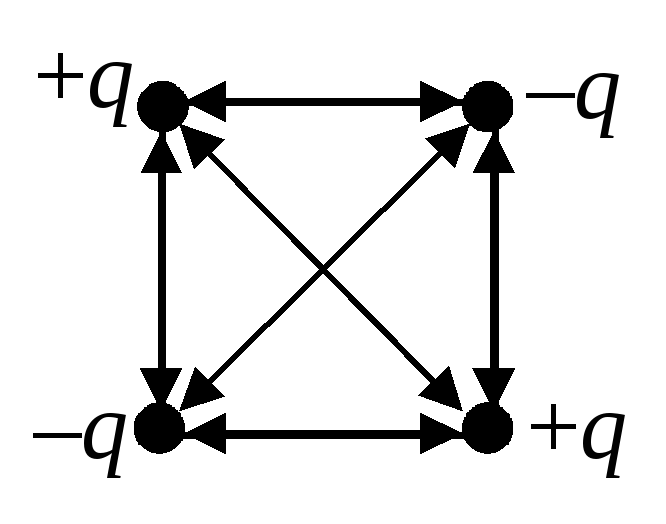
Determinați energia electrică de interacțiune a sarcinilor punctiforme situate la vârfurile unui pătrat cu latura A(vezi fig. 2).
Soluţie.
În Fig. 3, toate interacțiunile perechi ale sarcinilor sunt descrise în mod convențional prin săgeți dublu direcționate. Ținând cont de energiile tuturor acestor interacțiuni, obținem:
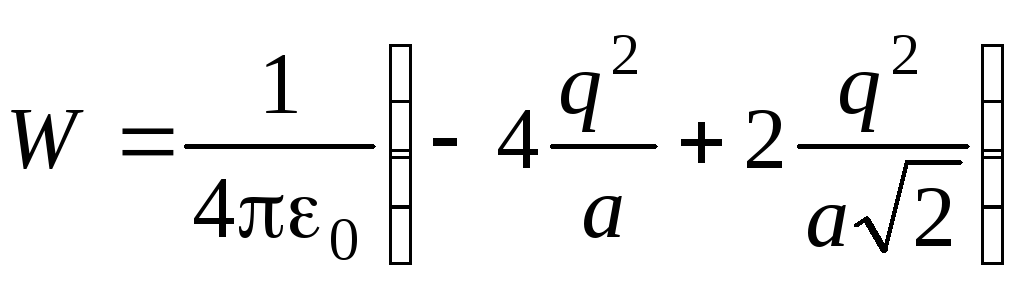 .
.
|
|
|
|
Exemplul 2.
Determinați energia electrică de interacțiune a unui inel încărcat cu un dipol situat pe axa sa, așa cum se arată în Fig. 4. Distanțe cunoscute A, l, taxe Q, qși raza inelului R.
Soluţie.
La rezolvarea problemei, ar trebui să se țină cont de toate energiile interacțiunilor de perechi ale sarcinilor unui corp (inel) cu sarcinile altui corp (dipol). Energia de interacțiune a unei sarcini punctiforme q cu taxa Q distribuit pe inel este determinat de suma
![]() ,
,
Unde 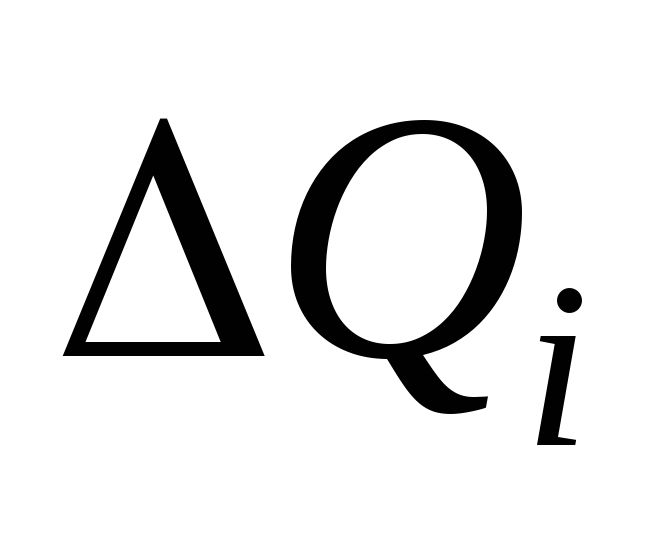 - sarcina unui fragment de inel infinitezimal,
- sarcina unui fragment de inel infinitezimal,
 -
distanta de la acest fragment la sarcina q. Pentru că totul
-
distanta de la acest fragment la sarcina q. Pentru că totul  aceleași și egale
aceleași și egale 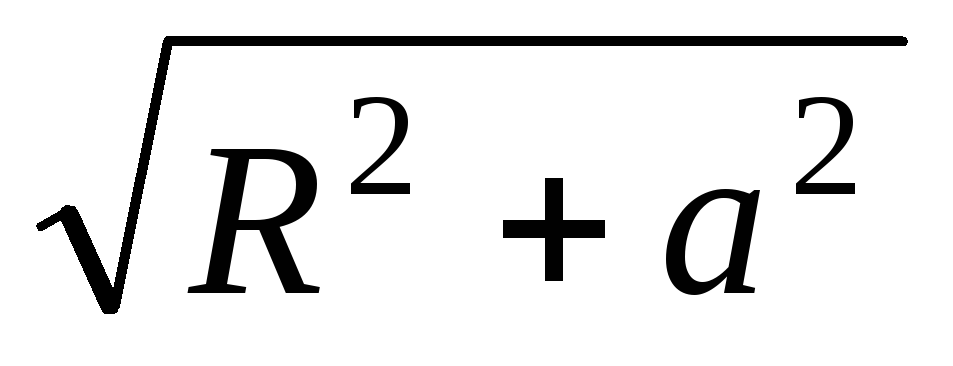 , Acea
, Acea
În mod similar, găsim energia de interacțiune a unei sarcini punctiforme - q cu inel încărcat:
Rezumând W 1 și W 2, obținem pentru energia de interacțiune a inelului cu dipolul:
 .
.
Energia electrică a conductoarelor încărcate
Exemplul 3.
Definiți locul de muncă forte electrice când raza unei sfere încărcate uniform scade cu un factor de 2. Încărcare sferă q, raza sa inițială R.
Soluţie.
Energia electrică a unui conductor solitar este determinată de formula 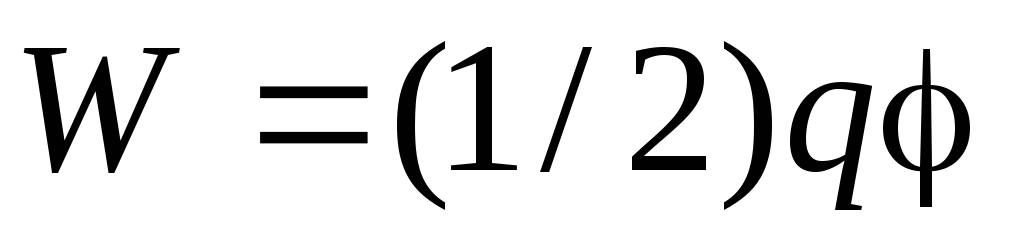 , Unde q– sarcina conductorului, – potenţialul acestuia. Având în vedere că potențialul unei sfere de rază încărcate uniform R egală
, Unde q– sarcina conductorului, – potenţialul acestuia. Având în vedere că potențialul unei sfere de rază încărcate uniform R egală  , să-i găsim energia electrică:
, să-i găsim energia electrică:
 .
.
După ce raza sferei este înjumătățită, energia ei devine egală cu
 .
.
Forțele electrice funcționează
 .
.
Exemplul 4.
Două bile metalice ale căror raze sunt rși 2 r, iar taxele corespunzătoare sunt 2 qȘi - q, situate în vid la mare distanță unul de celălalt. De câte ori va scădea energia electrică a sistemului dacă bilele sunt conectate cu un fir subțire?
Soluţie.
După conectarea bilelor cu un fir subțire, potențialele lor devin aceleași
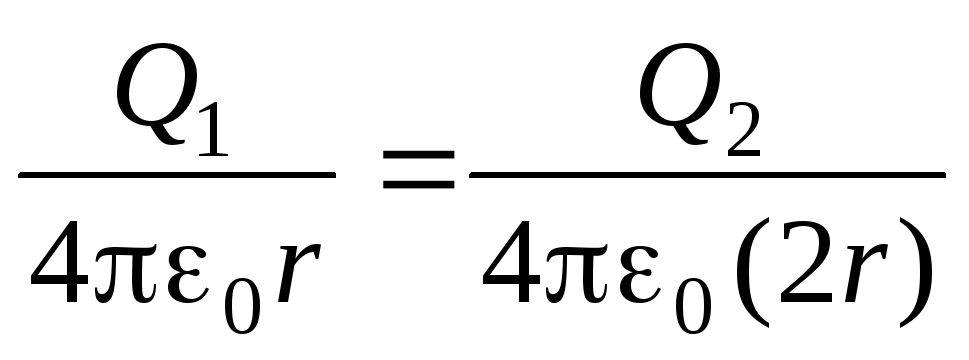 ,
,
și încărcările constante ale bilelor Q 1 și Q 2 sunt obținute ca urmare a fluxului de sarcină de la o minge la alta. În acest caz, sarcina totală a bilelor rămâne constantă:
 .
.
Din aceste ecuații găsim
 ,
, .
.
Energia bilelor înainte ca acestea să fie conectate prin sârmă este egală cu
 ,
,
si dupa conectare
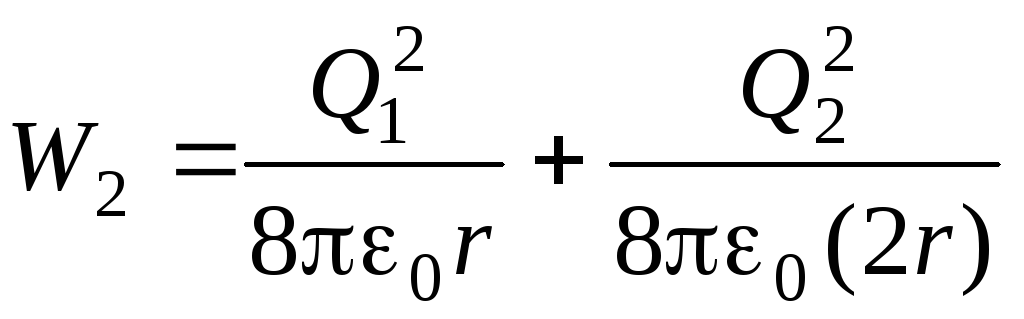 .
.
Înlocuirea valorilor în ultima expresie Q 1 și Q 2, obținem după transformări simple
 .
.
Exemplul 5.
Îmbinată într-o singură minge N= 8 bile identice de mercur, fiecare având o încărcătură q. Avand in vedere ca in starea initiala bilele de mercur erau aprinse distanta lunga unul de altul, determinați de câte ori a crescut energia electrică a sistemului.
Soluţie.
Când sferele de mercur se îmbină, încărcarea și volumul lor total sunt păstrate:
![]() ,
,
Unde Q- încărcarea mingii, R- raza sa, r este raza fiecărei bile mici de mercur. Energia electrică totală N bile solitare este egală cu
 .
.
Energia electrică a mingii rezultate
 .
.
După transformări algebrice obținem
 = 4.
= 4.
Exemplul 6.
Bilă cu rază de metal R= 1 mm și încărcați q= 0,1 nC de la mare distanță se apropie încet de un conductor neîncărcat și se opresc când potențialul bilei devine egal cu = 450 V. Ce lucru ar trebui făcut pentru aceasta?
Soluţie.
Energia electrică a unui sistem de doi conductori încărcați este determinată de formula
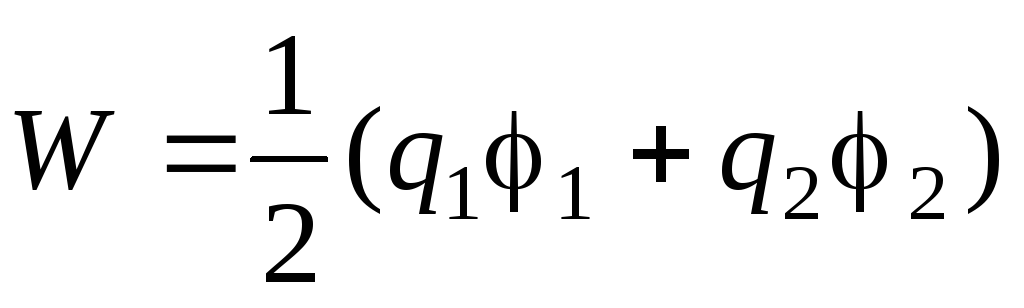 ,
,
Unde q 1 și q 2 – sarcinile conductoarelor, 1 și 2 – potențialele acestora. Deoarece conductorul conform problemei nu este încărcat, atunci
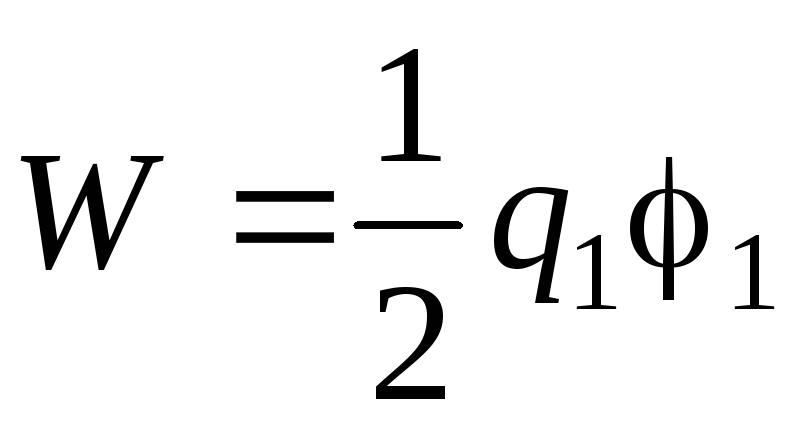 ,
,
Unde q 1 și 1 sarcină și potențialul mingii. Când mingea și conductorul neîncărcat sunt la o distanță mare unul de celălalt,
 ,
,
și energia electrică a sistemului
 .
.
În starea finală a sistemului, când potențialul bilei devine egal cu , energia electrică a sistemului este:
 .
.
Munca forțelor externe este egală cu creșterea energiei electrice:
 = –0,0225 µJ.
= –0,0225 µJ.
observa asta câmp electricîn starea finală a sistemului este creată de sarcinile induse pe conductor, precum și de sarcini distribuite neuniform pe suprafața bilei de metal. Este foarte dificil de calculat acest câmp cu o geometrie cunoscută a conductorului și o poziție dată a bilei metalice. Nu a fost nevoie să facem acest lucru, deoarece problema nu specifică configurația geometrică a sistemului, ci potențialul mingii în starea finală.
Exemplu 7 .
Sistemul este format din două carcase de metal subțiri concentrice cu raze R 1 și R 2
( și taxele corespunzătoare q 1 și q 2. Găsiți energie electrică W sisteme. Luați în considerare și cazul special când
și taxele corespunzătoare q 1 și q 2. Găsiți energie electrică W sisteme. Luați în considerare și cazul special când ![]() .
.
Soluţie.
Energia electrică a unui sistem de doi conductori încărcați este determinată de formula
 .
.
Pentru a rezolva problema, este necesar să găsim potențialele sferelor interne ( 1) și externe ( 2). Acest lucru nu este dificil de făcut (consultați secțiunea corespunzătoare a manualului):
 ,
, .
.
Înlocuind aceste expresii în formula pentru energie, obținem
 .
.
La ![]() energia este egală
energia este egală
 .
.
Întrebarea nr. 1
Câmp electric. Pentru a explica natura interacțiunilor electrice ale corpurilor încărcate, este necesar să presupunem prezența în spațiul care înconjoară sarcinile unui agent fizic care realizează această interacțiune. În conformitate cu teoria cu raza scurta de actiune, care afirmă că interacțiunile de forță dintre corpuri se desfășoară printr-un mediu material special care înconjoară corpurile care interacționează și transmit orice modificări ale acestor interacțiuni în spațiu cu o viteză finită, un astfel de agent este câmp electric.
Câmpul electric este creat atât de sarcinile staționare, cât și de cele în mișcare. Prezența unui câmp electric poate fi judecată, în primul rând, după capacitatea sa de a exercita un efect de forță asupra sarcini electrice, în mișcare și staționar, precum și prin capacitatea de a induce sarcini electrice pe suprafața corpurilor neutre conducătoare.
Câmpul creat de sarcini electrice staționare se numește electric staționar, sau electrostatic camp. Reprezinta caz special câmp electromagnetic, prin care se realizează interacțiuni de forță între corpuri încărcate electric care se deplasează în cazul general într-o manieră arbitrară față de sistemul de referință.
Intensitatea câmpului electric. O caracteristică cantitativă a acțiunii forței unui câmp electric asupra corpurilor încărcate este mărimea vectorială E, numit intensitatea câmpului electric.
E= F / q etc.
Este determinat de raportul de forță F, acționând din câmp pe o încărcare de testare punctuală q pr, plasat în punctul de câmp luat în considerare, la magnitudinea acestei sarcini.
Conceptul de „sarcină de test” presupune că această sarcină nu participă la crearea câmpului electric și este atât de mică încât nu o distorsionează, adică nu provoacă o redistribuire în spațiu a sarcinilor care creează câmpul. în cauză. Unitatea SI de tensiune este 1 V/m, ceea ce este echivalent cu 1 N/C.
Intensitatea câmpului unei sarcini punctiforme. Folosind legea lui Coulomb, găsim o expresie pentru intensitatea câmpului electric creat de o sarcină punctiformă qîntr-un mediu izotrop omogen la distanţă r din taxa:
În această formulă r– vectorul de rază a sarcinilor de legătură qȘi q etc. Din (1.2) rezultă că tensiunea E câmpuri de taxă punctuală qîn toate punctele câmpului este îndreptată radial de la sarcina la q> 0 și pentru a încărca la q< 0.
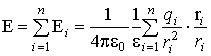 Principiul suprapunerii. Puterea câmpului generate de sistem taxe punctiforme staționare q 1 , q 2 , q 3, ¼, qn, este egal cu suma vectorială a intensităților câmpului electric creat de fiecare dintre aceste sarcini separat:
Principiul suprapunerii. Puterea câmpului generate de sistem taxe punctiforme staționare q 1 , q 2 , q 3, ¼, qn, este egal cu suma vectorială a intensităților câmpului electric creat de fiecare dintre aceste sarcini separat:
, Unde r i– distanța dintre încărcare q iși punctul de câmp considerat.
Principiul suprapunerii, vă permite să calculați nu numai intensitatea câmpului unui sistem de sarcini punctuale, ci și intensitatea câmpului în sistemele în care există o distribuție continuă a încărcăturii. Sarcina unui corp poate fi reprezentată ca suma sarcinilor punctiforme elementare d q.
Mai mult, dacă taxa este distribuită cu densitate liniară t, apoi d q= td l; dacă taxa este distribuită cu densitatea suprafeței s, apoi d q=d lși d q= rd l, dacă taxa este distribuită cu densitate în vrac r.
Întrebarea nr. 2
Flux vectorial de inducție electrică. Fluxul vectorului de inducție electrică este determinat în mod similar cu fluxul vectorului intensității câmpului electric
dF D = D d S
Există o oarecare ambiguitate în definițiile fluxurilor datorită faptului că pentru fiecare suprafață pot fi specificate două normale de direcții opuse. Pentru o suprafață închisă, normala exterioară este considerată pozitivă.
teorema lui Gauss. Să considerăm o sarcină electrică pozitivă punctiformă q situată în interiorul unei suprafețe închise arbitrare S (Fig. 1.3). Fluxul vectorului de inducție prin elementul de suprafață dS este egal cu ![]()
Componenta dS D = dS cosa elementului de suprafață d Sîn direcția vectorului de inducție Dîl considerăm ca un element al unei suprafețe sferice de rază r, în centrul căreia se află o sarcină q.
Ținând cont de faptul că dS D / r 2 este egal cu unghiul solid elementar dw, la care elementul de suprafață dS este vizibil din punctul în care se află sarcina q, transformăm expresia (1.4) în forma dF D = q dw / 4p, de unde, după integrarea pe întreg spațiul care înconjoară sarcina, adică în unghiul solid de la 0 la 4p, obținem
Fluxul vectorului de inducție electrică printr-o suprafață închisă de formă arbitrară este egal cu sarcina conținută în această suprafață.
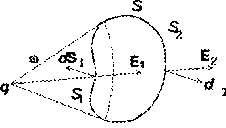
Dacă o suprafață închisă arbitrară S nu acoperă o sarcină punctiformă q, atunci, construind o suprafață conică cu vârful în punctul în care se află sarcina, împărțim suprafața S în două părți: S 1 și S 2. Vector de flux D prin suprafața S găsim ca sumă algebrică a fluxurilor prin suprafețele S 1 și S 2:
![]() .
.
Ambele suprafețe din punctul în care se află sarcina q sunt vizibile la același unghi solid w. Prin urmare, debitele sunt egale
Deoarece normala exterioară la suprafață este utilizată la calcularea debitului printr-o suprafață închisă, este ușor de observat că debitul Ф 1D< 0, тогда как поток Ф 2D >0. Flux total Ф D = 0. Aceasta înseamnă că fluxul vectorului de inducție electrică printr-o suprafață închisă de formă arbitrară nu depinde de sarcinile situate în afara acestei suprafețe.
Dacă câmpul electric este creat de un sistem de sarcini punctiforme q 1, q 2,¼, q n, care este acoperit de o suprafață închisă S, atunci, în conformitate cu principiul suprapunerii, fluxul vectorului de inducție prin această suprafață este determinată ca suma fluxurilor create de fiecare dintre sarcini. Fluxul vectorului de inducție electrică printr-o suprafață închisă de formă arbitrară este egal cu suma algebrică a sarcinilor acoperite de această suprafață:
Trebuie remarcat faptul că taxele q i nu trebuie să fie punctuale, conditie necesara- zona incarcata trebuie sa fie complet acoperita de suprafata. Dacă în spațiul delimitat de o suprafață închisă S, sarcina electrică este distribuită continuu, atunci ar trebui să presupunem că fiecare volum elementar dV are o sarcină. În acest caz, în partea dreaptă a expresiei, însumarea algebrică a sarcinilor este înlocuită cu integrarea peste volumul închis în interiorul suprafeței închise S:
Această expresie este formularea cea mai generală a teoremei lui Gauss: fluxul vectorului de inducție electrică printr-o suprafață închisă de formă arbitrară este egal cu sarcina totală din volumul acoperit de această suprafață și nu depinde de sarcinile situate în afara suprafeței în cauză. ![]() .
.
Întrebarea #3
Energia potențială a unei sarcini într-un câmp electric. Lucru efectuat de forțele câmpului electric atunci când se deplasează o sarcină punctiformă pozitivă q de la poziția 1 la poziția 2, imaginați-vă ca o schimbare a energiei potențiale a acestei sarcini: ![]() , Unde W p1 și W p2 – energii potențiale de încărcare qîn poziţiile 1 şi 2. Cu mişcare mică de încărcare qîn câmpul creat de o sarcină punctiformă pozitivă Q, modificarea energiei potenţiale este
, Unde W p1 și W p2 – energii potențiale de încărcare qîn poziţiile 1 şi 2. Cu mişcare mică de încărcare qîn câmpul creat de o sarcină punctiformă pozitivă Q, modificarea energiei potenţiale este ![]() . La mișcarea finală de încărcare q de la poziția 1 la poziția 2, situată la distanțe r 1 și r 2 din taxă Q, . Dacă câmpul este creat de un sistem de taxe punctiforme Q 1 ,Q 2 ¼, Q n , apoi modificarea energiei potențiale a sarcinii qîn acest domeniu:
. La mișcarea finală de încărcare q de la poziția 1 la poziția 2, situată la distanțe r 1 și r 2 din taxă Q, . Dacă câmpul este creat de un sistem de taxe punctiforme Q 1 ,Q 2 ¼, Q n , apoi modificarea energiei potențiale a sarcinii qîn acest domeniu:  . Formulele date ne permit să găsim doar Schimbare energia potenţială a unei sarcini punctiforme q, și nu energia potențială în sine. Pentru a determina energia potențială, este necesar să se convină în ce punct al câmpului ar trebui considerată egală cu zero. Pentru energia potențială a unei sarcini punctiforme q situat într-un câmp electric creat de o altă sarcină punctuală Q, primim
. Formulele date ne permit să găsim doar Schimbare energia potenţială a unei sarcini punctiforme q, și nu energia potențială în sine. Pentru a determina energia potențială, este necesar să se convină în ce punct al câmpului ar trebui considerată egală cu zero. Pentru energia potențială a unei sarcini punctiforme q situat într-un câmp electric creat de o altă sarcină punctuală Q, primim
![]() , Unde C– constantă arbitrară. Fie ca energia potențială să fie zero la o distanță infinit de mare de sarcină Q(la r® ¥), apoi constanta C= 0 iar expresia anterioară ia forma . În acest caz, energia potențială este definită ca munca de deplasare a unei sarcini cu ajutorul forțelor câmpului dintr-un punct dat la un punct infinit îndepărtat.În cazul unui câmp electric creat de un sistem de sarcini punctuale, energia potenţială a sarcinii q:
, Unde C– constantă arbitrară. Fie ca energia potențială să fie zero la o distanță infinit de mare de sarcină Q(la r® ¥), apoi constanta C= 0 iar expresia anterioară ia forma . În acest caz, energia potențială este definită ca munca de deplasare a unei sarcini cu ajutorul forțelor câmpului dintr-un punct dat la un punct infinit îndepărtat.În cazul unui câmp electric creat de un sistem de sarcini punctuale, energia potenţială a sarcinii q:
![]() .
.
![]() Energia potențială a unui sistem de sarcini punctiforme.În cazul unui câmp electrostatic, energia potențială servește ca măsură a interacțiunii sarcinilor. Să existe un sistem de sarcini punctuale în spațiu Q i(i = 1, 2, ... , n). Energia interacțiunii tuturor n taxele este determinată de relația, unde r ij - distanța dintre sarcinile corespunzătoare și însumarea se realizează astfel încât interacțiunea dintre fiecare pereche de sarcini să fie luată în considerare o singură dată.
Energia potențială a unui sistem de sarcini punctiforme.În cazul unui câmp electrostatic, energia potențială servește ca măsură a interacțiunii sarcinilor. Să existe un sistem de sarcini punctuale în spațiu Q i(i = 1, 2, ... , n). Energia interacțiunii tuturor n taxele este determinată de relația, unde r ij - distanța dintre sarcinile corespunzătoare și însumarea se realizează astfel încât interacțiunea dintre fiecare pereche de sarcini să fie luată în considerare o singură dată.
Potențial de câmp electrostatic. Câmpul unei forțe conservative poate fi descris nu numai printr-o funcție vectorială, dar o descriere echivalentă a acestui câmp poate fi obținută prin definirea unei mărimi scalare adecvate în fiecare dintre punctele sale. Pentru un câmp electrostatic, această mărime este potenţial de câmp electrostatic, definit ca raportul dintre energia potențială a sarcinii de testare q la mărimea acestei sarcini, j = W P / q, din care rezultă că potențialul este numeric egal cu energia potențială deținută de o sarcină pozitivă unitară într-un punct dat al câmpului. Unitatea de măsură pentru potențial este Volt (1 V).
Potențial de câmp de sarcină punctiformăQîntr-un mediu izotrop omogen cu constantă dielectrică e: .
![]()
![]() Principiul suprapunerii. Potențialul este o funcție scalară; principiul suprapunerii este valabil pentru acesta. Deci pentru potențialul de câmp al unui sistem de sarcini punctuale Q 1, Q 2 ¼, Qn avem unde r i- distanta de la un punct de camp cu potential j la sarcina Q i. Dacă sarcina este distribuită în mod arbitrar în spațiu, atunci unde r- distanta fata de volumul elementar d X,d y,d z la punctul ( X, y, z), unde potenţialul este determinat; V- volumul spațiului în care este distribuită sarcina.
Principiul suprapunerii. Potențialul este o funcție scalară; principiul suprapunerii este valabil pentru acesta. Deci pentru potențialul de câmp al unui sistem de sarcini punctuale Q 1, Q 2 ¼, Qn avem unde r i- distanta de la un punct de camp cu potential j la sarcina Q i. Dacă sarcina este distribuită în mod arbitrar în spațiu, atunci unde r- distanta fata de volumul elementar d X,d y,d z la punctul ( X, y, z), unde potenţialul este determinat; V- volumul spațiului în care este distribuită sarcina.
Potențialul și munca forțelor câmpului electric. Pe baza definiției potențialului, se poate demonstra că munca efectuată de câmpul electric forțează la deplasarea unei sarcini punctiforme q de la un punct al câmpului la altul este egal cu produsul dintre mărimea acestei sarcini și diferența de potențial la punctele inițiale și finale ale traseului, A = q(j 1 - j 2).
Este convenabil să scrieți definiția după cum urmează:
Întrebarea #4
Pentru a stabili o legătură între forța caracteristică câmpului electric - tensiuneși caracteristicile sale energetice - potenţial Să luăm în considerare munca elementară a forțelor câmpului electric asupra unei deplasări infinitezimale a unei sarcini punctiforme q:d A = qE d l, același lucru este egal cu scăderea energiei potențiale a sarcinii q:d A = - d W P = - q d, unde d este modificarea potențialului câmpului electric pe lungimea călătoriei d l. Echivalând părțile din dreapta ale expresiilor, obținem: E d l= -d sau în sistem de coordonate carteziene
ex d x + E y d y + E z d z =-d, (1,8)
Unde ex,E y,Ez- proiectii ale vectorului tensiune pe axele sistemului de coordonate. Deoarece expresia (1.8) este o diferenţială totală, atunci pentru proiecţiile vectorului intensitate avem
![]() Unde .
Unde .
Expresia dintre paranteze este gradient potenţialul j, adică
E= - grad = -Ñ .
Intensitatea în orice punct al câmpului electric este egală cu gradientul de potențial din acest punct, luat cu semnul opus. Semnul minus indică faptul că tensiunea Eîndreptată spre scăderea potenţialului.
Luați în considerare câmpul electric creat de o sarcină punctiformă pozitivă q(Fig. 1.6). Potențial de câmp într-un punct M, a cărui poziţie este determinată de vectorul rază r, egal = q/ 4pe 0 e r. Direcția vectorului de rază r coincide cu direcția vectorului de tensiune E, iar gradientul de potențial este îndreptat în direcția opusă. Proiecția gradientului pe direcția vectorului rază
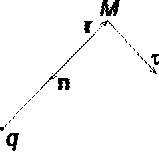
![]() . Proiecția gradientului de potențial pe direcția vectorului t, perpendicular pe vector r, este egal
. Proiecția gradientului de potențial pe direcția vectorului t, perpendicular pe vector r, este egal ![]() ,
,
adică în această direcție potențialul câmpului electric este valoare constantă( = const).
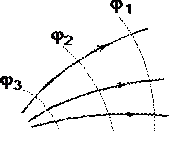 În cazul luat în considerare, direcția vectorului r coincide cu directia
În cazul luat în considerare, direcția vectorului r coincide cu directia
linii de înaltă tensiune. Rezumând rezultatul obținut, se poate afirma că în toate punctele curbei ortogonale cu liniile de forță, potențialul câmpului electric este același. Locul geometric al punctelor cu același potențial este o suprafață echipotențială ortogonală cu liniile de forță.
Atunci când descrieți grafic câmpurile electrice, sunt adesea folosite suprafețele echipotențiale. De obicei, echipotențialele sunt desenate în așa fel încât diferența de potențial dintre oricare două suprafețe echipotențiale să fie aceeași. Iată o imagine bidimensională a câmpului electric. Liniile de câmp sunt afișate ca linii continue, echipotenţialele ca linii întrerupte.
O astfel de imagine ne permite să spunem în ce direcție este îndreptat vectorul intensității câmpului electric; unde tensiunea este mai mare, unde este mai mică; unde o sarcină electrică plasată într-unul sau altul punct al câmpului va începe să se miște. Deoarece toate punctele de pe o suprafață echipotențială sunt la același potențial, deplasarea unei sarcini de-a lungul ei nu necesită muncă. Aceasta înseamnă că forța care acționează asupra sarcinii este întotdeauna perpendiculară pe deplasare.
Întrebarea #5
Dacă conductorului i se dă o sarcină în exces, atunci această sarcină distribuite pe suprafața conductorului. Într-adevăr, dacă în interiorul unui conductor selectăm o suprafață închisă arbitrară S, atunci fluxul vectorului intensității câmpului electric prin această suprafață ar trebui să fie egal cu zero. În caz contrar, în interiorul conductorului va exista un câmp electric, care va duce la mișcarea sarcinilor. Prin urmare, pentru ca condiția să fie îndeplinită
Sarcina electrică totală din interiorul acestei suprafețe arbitrare trebuie să fie zero.
Intensitatea câmpului electric lângă suprafața unui conductor încărcat poate fi determinată folosind teorema lui Gauss. Pentru a face acest lucru, selectăm o mică zonă arbitrară d pe suprafața conductorului S si, considerandu-l ca baza, construim pe el un cilindru cu generatoare d l(Fig. 3.1). Vector pe suprafața conductorului Eîndreptată normal către această suprafaţă. Prin urmare fluxul vectorial E prin suprafața laterală a cilindrului datorită micii lui d l egal cu zero. Fluxul acestui vector prin baza inferioară a cilindrului, situată în interiorul conductorului, este, de asemenea, zero, deoarece în interiorul conductorului nu există câmp electric. Prin urmare, fluxul vectorial E prin întreaga suprafață a cilindrului este egală cu debitul prin acesta baza de sus d S": , unde E n este proiecția vectorului intensității câmpului electric pe normala externă n la amplasament d S. 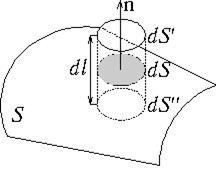
Conform teoremei lui Gauss, acest flux este egal cu suma algebrică a sarcinilor electrice acoperite de suprafața cilindrului, împărțită la produsul constantei electrice și permitivitatea relativă a mediului care înconjoară conductorul. În interiorul cilindrului există o sarcină, unde este densitatea sarcinii de suprafață. Prin urmare ![]() și, adică intensitatea câmpului electric lângă suprafața unui conductor încărcat este direct proporțională cu densitatea suprafeței sarcinilor electrice situate pe această suprafață.
și, adică intensitatea câmpului electric lângă suprafața unui conductor încărcat este direct proporțională cu densitatea suprafeței sarcinilor electrice situate pe această suprafață.
Studii experimentale ale distribuției sarcinilor în exces pe conductori diverse forme a arătat că distribuţia sarcinilor pe suprafaţa exterioară a conductorului depinde doar de forma suprafeței: cu cât curbura suprafeței este mai mare (cu cât raza de curbură este mai mică), cu atât densitatea de sarcină a suprafeței este mai mare.
În apropierea zonelor cu raze mici de curbură, în special în apropierea vârfului, din cauza valorilor mari de tensiune, are loc ionizarea gazelor, de exemplu a aerului. Ca urmare, ionii cu aceeași sarcină ca și conductorul se mișcă în direcția de la suprafața conductorului, iar ionii semnul opus la suprafața conductorului, ceea ce duce la o scădere a sarcinii conductorului. Acest fenomen se numește drenaj de sarcină.
Există încărcături în exces pe suprafețele interioare ale conductoarelor goale închise nici unul.
Dacă un conductor încărcat este adus în contact cu suprafata exterioara conductor neîncărcat, atunci sarcina va fi redistribuită între conductori până când potențialele lor devin egale.
Dacă același conductor încărcat atinge suprafata interioara conductor gol, apoi sarcina este transferată complet la conductorul gol.
În concluzie, remarcăm încă un fenomen inerent doar conductorilor. Dacă un conductor neîncărcat este plasat într-un câmp electric extern, atunci părțile sale opuse în direcția câmpului vor avea sarcini de semne opuse. Dacă, fără a elimina câmpul exterior, conductorul este divizat, atunci părțile separate vor avea sarcini opuse. Acest fenomen se numește inducție electrostatică.
Întrebarea #8
Toate substanțele, în funcție de capacitatea lor de a conduce curentul electric, sunt împărțite în conductoare, dielectriceȘi semiconductori. Conductorii sunt substanțe în care particulele încărcate electric - purtători de taxe- capabil să se miște liber pe întregul volum al substanței. Conductorii includ metale, soluții de săruri, acizi și alcaline, săruri topite, gaze ionizate.
Să ne limităm considerația conductoare metalice solide, având structură cristalină. Experimentele arată că, cu o diferență de potențial foarte mică aplicată unui conductor, electronii de conducție conținute în acesta încep să se miște și să se miște în volumul metalelor aproape liber.
În absența unui câmp electrostatic extern, câmpurile electrice ale ionilor pozitivi și ale electronilor de conducție sunt compensate reciproc, astfel încât puterea câmpului rezultat intern este zero.
La introducerea unui conductor metalic într-un câmp electrostatic extern cu o tensiune E 0 Forțele coulombiene îndreptate în direcții opuse încep să acționeze asupra ionilor și electronilor liberi. Aceste forțe determină deplasarea particulelor încărcate în interiorul metalului și, în principal, electronii liberi sunt deplasați, iar ionii pozitivi aflați la nodurile rețelei cristaline practic nu își schimbă poziția. Ca urmare, un câmp electric cu o intensitate de E".
Deplasarea particulelor încărcate în interiorul conductorului se oprește atunci când puterea totală a câmpului Eîntr-un conductor, egal cu suma puterilor câmpurilor externe și interne, va deveni egal cu zero: ![]()
Să prezentăm o expresie care conectează intensitatea și potențialul câmpului electrostatic sub următoarea formă:
Unde E- puterea câmpului rezultat în interiorul conductorului; n- normală internă la suprafaţa conductorului. De la egalitatea la zero a tensiunii rezultate E rezultă că în în volumul conductorului, potențialul are aceeași valoare: .
Rezultatele obținute ne permit să tragem trei concluzii importante:
1. În toate punctele din interiorul conductorului, intensitatea câmpului, adică întregul volum al conductorului echipotenţială.
2. Cu o distribuție statică a sarcinilor de-a lungul unui conductor, vectorul de tensiune E pe suprafața sa trebuie îndreptată normal față de suprafață, în caz contrar, sub influența componentelor de tensiune tangente la suprafața conductorului, sarcinile trebuie să se deplaseze de-a lungul conductorului.
3. Suprafața conductorului este și echipotențială, deoarece pentru orice punct de pe suprafață
![]()
Întrebarea #10
Dacă doi conductori au o astfel de formă încât câmpul electric pe care îl creează este concentrat într-o zonă limitată a spațiului, atunci sistemul format de ei se numește condensator, iar conducătorii înșiși sună căptușeli condensator.
Condensator sferic. Două conductoare în formă de sfere concentrice cu raze R 1 și R 2 (R 2 > R 1), formează un condensator sferic. Folosind teorema lui Gauss, este ușor de demonstrat că câmpul electric există doar în spațiul dintre sfere. Puterea acestui câmp ![]() ,
,
Unde q- sarcina electrică a sferei interioare; - constanta dielectrica relativa a mediului care umple spatiul dintre placi; r- distanta fata de centrul sferelor, si R 1 r R 2. Diferența potențială între plăci  și capacitatea unui condensator sferic.
și capacitatea unui condensator sferic.
Condensator cilindric este format din doi cilindri coaxiali conductori cu raze R 1 și R 2 (R 2 > R 1). Neglijând efectele marginilor de la capetele cilindrilor și presupunând că spațiul dintre plăci este umplut cu un mediu dielectric cu permeabilitate relativă, intensitatea câmpului din interiorul condensatorului poate fi găsită prin formula: ![]() ,
,
Unde q- sarcina cilindrului interior; h- inaltimea cilindrilor (garniturilor); r- distanta fata de axa cilindrului. În consecință, diferența de potențial dintre plăcile unui condensator cilindric și capacitatea acestuia este 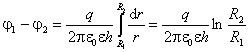 . .
. .
Condensator plat. Două plăci paralele plate de aceeași zonă S situat la distanta d unul de altul, formă condensator plat. Dacă spațiul dintre plăci este umplut cu un mediu cu o constantă dielectrică relativă, atunci când le este conferită o sarcină q intensitatea câmpului electric dintre plăci este egală cu , diferența de potențial este egală cu . Astfel, capacitatea unui condensator cu plăci paralele este .
Conectarea în serie și paralelă a condensatoarelor.
La conexiune serială n condensatoare, capacitatea totală a sistemului este egală cu
Conexiune paralelă n condensatorii formează un sistem, a cărui capacitate electrică poate fi calculată după cum urmează:
Întrebarea nr. 11
Energia unui conductor încărcat. Suprafața conductorului este echipotențială. Prin urmare, potențialele acelor puncte în care sunt situate sarcinile punctuale d q, sunt identice și egale cu potențialul conductorului. Încărca q, situat pe conductor, poate fi considerat ca un sistem de sarcini punctuale d q. Apoi energia conductorului încărcat
Ținând cont de definiția capacității, putem scrie
Oricare dintre aceste expresii determină energia unui conductor încărcat.
Energia unui condensator încărcat. Fie potențialul plăcii condensatorului pe care sarcina este + q, este egal cu , iar potențialul plăcii pe care se află sarcina este q, este egal cu . Energia unui astfel de sistem
Energia unui condensator încărcat poate fi reprezentată ca
Energia câmpului electric. Energia unui condensator încărcat poate fi exprimată în termeni de mărimi care caracterizează câmpul electric din golul dintre plăci. Să facem asta folosind exemplul unui condensator plat. Înlocuirea expresiei pentru capacitate în formula pentru energia condensatorului dă
Privat U / d egală cu puterea câmpului în decalaj; muncă S· d reprezintă volumul V ocupat de câmp. Prin urmare, ![]()
Dacă câmpul este uniform (ceea ce este cazul într-un condensator plat la distanță d mult mai mici decât dimensiunile liniare ale plăcilor), atunci energia conținută în el este distribuită în spațiu cu o densitate constantă w. Apoi densitatea energiei volumetrice câmpul electric este egal
![]()
Ținând cont de relație, putem scrie
Într-un dielectric izotrop, direcțiile vectorilor DȘi E coincid și
Înlocuind expresia , obținem
Primul termen din această expresie coincide cu densitatea energiei câmpului în vid. Al doilea termen reprezintă energia cheltuită pentru polarizarea dielectricului. Să demonstrăm acest lucru folosind exemplul unui dielectric nepolar. Polarizarea unui dielectric nepolar constă în faptul că sarcinile care alcătuiesc moleculele sunt deplasate din pozițiile lor sub influența unui câmp electric. E. Pe unitatea de volum de dielectric, lucru cheltuit la sarcinile de deplasare q i prin valoare d r eu, este
Expresia dintre paranteze este momentul dipolar pe unitate de volum sau polarizarea dielectricului R. Prin urmare, .
Vector P asociat cu un vector E raport Înlocuind această expresie în formula pentru lucru, obținem
După ce am realizat integrarea, determinăm munca cheltuită pentru polarizarea unei unități de volum de dielectric.
Cunoscând densitatea energiei câmpului în fiecare punct, puteți găsi energia câmpului conținută în orice volum V. Pentru a face acest lucru, trebuie să calculați integrala: ![]()
Densitatea energiei câmpului electrostatic
Folosind (66), (50), (53), transformăm formula pentru energia condensatorului după cum urmează: , unde este volumul condensatorului. Să împărțim ultima expresie la: ![]() . Valoarea are semnificația densității de energie a câmpului electrostatic.
. Valoarea are semnificația densității de energie a câmpului electrostatic.
Întrebarea #12
Un dielectric plasat într-un câmp electric extern polarizează sub influenţa acestui domeniu. Polarizarea unui dielectric este procesul de dobândire a unui moment dipolar macroscopic diferit de zero.
Gradul de polarizare al unui dielectric este caracterizat de o mărime vectorială numită polarizare sau vector de polarizare (P). Polarizarea este definită ca momentul electric pe unitatea de volum a dielectricului,
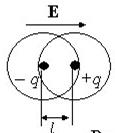 Unde N- numărul de molecule în volum. Polarizare P adesea numită polarizare, adică prin aceasta o măsură cantitativă a acestui proces.
Unde N- numărul de molecule în volum. Polarizare P adesea numită polarizare, adică prin aceasta o măsură cantitativă a acestui proces.
In dielectrici se disting urmatoarele tipuri de polarizare: electronica, orientativa si latice (pentru cristale ionice).
Tip de polarizare electronică caracteristică dielectricilor cu molecule nepolare. Într-un câmp electric extern, sarcinile pozitive din interiorul moleculei sunt deplasate în direcția câmpului, iar sarcinile negative în direcția opusă, în urma cărora moleculele capătă un moment dipolar îndreptat de-a lungul câmpului extern.
 Momentul dipol indus al unei molecule este proporțional cu puterea câmpului electric extern, unde este polarizabilitatea moleculei. Valoarea polarizării în acest caz este egală cu , unde n- concentrarea moleculelor; - momentul dipol indus al unei molecule, care este același pentru toate moleculele și a cărui direcție coincide cu direcția câmpului exterior.
Momentul dipol indus al unei molecule este proporțional cu puterea câmpului electric extern, unde este polarizabilitatea moleculei. Valoarea polarizării în acest caz este egală cu , unde n- concentrarea moleculelor; - momentul dipol indus al unei molecule, care este același pentru toate moleculele și a cărui direcție coincide cu direcția câmpului exterior.
Tipul de orientare de polarizare caracteristică dielectricilor polari. În absența unui câmp electric extern, dipolii moleculari sunt orientați aleatoriu, astfel încât momentul electric macroscopic al dielectricului este zero.
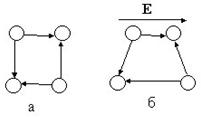 Dacă plasați un astfel de dielectric într-un câmp electric extern, atunci un moment de forță va acționa asupra moleculei dipolului (Fig. 2.2), având tendința de a-și orienta momentul dipolului în direcția intensității câmpului. Cu toate acestea, orientarea completă nu are loc, deoarece mișcarea termică tinde să distrugă efectul câmpului electric extern.
Dacă plasați un astfel de dielectric într-un câmp electric extern, atunci un moment de forță va acționa asupra moleculei dipolului (Fig. 2.2), având tendința de a-și orienta momentul dipolului în direcția intensității câmpului. Cu toate acestea, orientarea completă nu are loc, deoarece mișcarea termică tinde să distrugă efectul câmpului electric extern.
Această polarizare se numește orientativă. Polarizarea în acest caz este egală cu , unde<p> este valoarea medie a componentei momentului dipolar al moleculei în direcția câmpului exterior.
Tipul rețelei de polarizare caracteristic cristalelor ionice. În cristalele ionice (NaCl etc.) în absența unui câmp extern, momentul dipol al fiecărei celule unitate este zero (Fig. 2.3.a), sub influența unui câmp electric extern, ionii pozitivi și negativi sunt deplasați în directii opuse (Fig. 2.3.b) . Fiecare celulă a cristalului devine un dipol, cristalul este polarizat. Această polarizare se numește zăbrele. Polarizarea în acest caz poate fi definită și ca , unde este valoarea momentului dipol al celulei unitare, n- numărul de celule pe unitatea de volum.
Polarizarea dielectricilor izotropi de orice tip este legată de intensitatea câmpului prin relația, unde - susceptibilitate dielectrică dielectric.
Întrebarea nr. 13
Polarizarea unui mediu are o proprietate remarcabilă: fluxul vectorului de polarizare al mediului printr-o suprafață închisă arbitrară este numeric egal cu valoarea sarcinilor „legate” necompensate din interiorul acestei suprafețe, luate cu semnul opus:
![]() (1). În formularea locală, proprietatea descrisă este descrisă de relație
(1). În formularea locală, proprietatea descrisă este descrisă de relație
(2) , unde este densitatea de volum a sarcinilor „legate”. Aceste relații se numesc teorema Gauss pentru polarizarea mediului (vector de polarizare) în forme integrale și, respectiv, diferențiale. Dacă teorema lui Gauss pentru intensitatea câmpului electric este o consecință a legii lui Coulomb sub formă de „câmp”, atunci teorema lui Gauss pentru polarizare este o consecință a definiției acestei mărimi.
Să demonstrăm relația (1), atunci relația (2) va fi valabilă datorită teoremei matematice Ostrogradsky-Gauss.
Să considerăm un dielectric de molecule nepolare cu o concentrație în volum a acestora din urmă egală cu . Credem că, sub influența unui câmp electric, sarcinile pozitive s-au deplasat din poziția de echilibru cu o cantitate, iar sarcinile negative cu o cantitate. Fiecare moleculă a dobândit un moment electric ![]() , iar volumul unitar a dobândit un moment electric. Să considerăm o suprafață închisă arbitrară suficient de netedă în dielectricul care este descris. Să presupunem că suprafața este desenată în așa fel încât, în absența unui câmp electric, „nu traversează” dipolii individuali, adică sarcinile pozitive și negative asociate cu structura moleculară a substanței „se compensează” reciproc. .
, iar volumul unitar a dobândit un moment electric. Să considerăm o suprafață închisă arbitrară suficient de netedă în dielectricul care este descris. Să presupunem că suprafața este desenată în așa fel încât, în absența unui câmp electric, „nu traversează” dipolii individuali, adică sarcinile pozitive și negative asociate cu structura moleculară a substanței „se compensează” reciproc. .
Rețineți, apropo, că relațiile (1) și (2) pentru și sunt satisfăcute identic.
Sub influența unui câmp electric, un element de suprafață va fi străbătut de sarcini pozitive din volum în cantitate de . Pentru sarcini negative avem valorile corespunzătoare și . Sarcina totală transferată către partea „exterioară” a elementului de suprafață (amintim că - normala exterioară la în raport cu volumul acoperit de suprafață) este egală cu
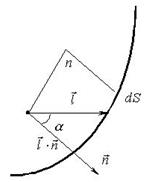
Proprietăți ale vectorului de polarizare al mediului
Prin integrarea expresiei rezultate pe o suprafață închisă, obținem valoarea sarcinii electrice totale care a lăsat volumul luat în considerare. Acesta din urmă ne permite să concluzionăm că în volumul luat în considerare rămâne o sarcină necompensată - egală ca mărime cu sarcina părăsită. Ca rezultat avem: ![]() , astfel se dovedește teorema Gauss pentru un câmp vectorial în formularea integrală.
, astfel se dovedește teorema Gauss pentru un câmp vectorial în formularea integrală.
Pentru a lua în considerare cazul unei substanțe formate din molecule polare, este suficient în raționamentul de mai sus să înlocuim cantitatea cu valoarea sa medie.
Dovada validității relației (1) poate fi considerată completă.
Întrebarea nr. 14
Într-un mediu dielectric pot fi prezente sarcini electrice de două tipuri: „liber” și „legat”. Primele dintre ele nu au legătură cu structura moleculară a substanței și, de regulă, se pot mișca relativ liber în spațiu. Acestea din urmă sunt asociate cu structura moleculară a substanței și, sub influența unui câmp electric, pot fi deplasate de la poziția de echilibru, de regulă, pe distanțe foarte scurte.
Utilizarea directă a teoremei Gauss pentru un câmp vectorial atunci când se descrie un mediu dielectric este incomod, deoarece partea dreaptă a formulei
![]() (1), conține atât valoarea încărcărilor „libere”, cât și valoarea sarcinilor „legate” (necompensate) în interiorul suprafeței închise.
(1), conține atât valoarea încărcărilor „libere”, cât și valoarea sarcinilor „legate” (necompensate) în interiorul suprafeței închise.
Dacă relația (1) se adaugă termen cu termen cu relația ![]() , primim
, primim ![]() , (2)
, (2)
unde este sarcina totală „liberă” a volumului acoperit de suprafața închisă. Relația (2) determină oportunitatea introducerii unui vector special
Ca mărime calculată convenabilă care caracterizează câmpul electric într-un mediu dielectric. Vectorul a fost numit anterior vector de inducție electrică sau vector de deplasare electrică. Termenul „vector” este utilizat în prezent. Pentru un câmp vectorial, forma integrală a teoremei lui Gauss este valabilă: ![]() și, în consecință, forma diferențială a teoremei lui Gauss:
și, în consecință, forma diferențială a teoremei lui Gauss:
unde este densitatea de volum a taxelor gratuite.
Dacă relația este validă (pentru electreți rigidi nu este validă), atunci pentru vectorul din definiția (3) rezultă:
unde este constanta dielectrică a mediului, una dintre cele mai importante caracteristici electrice ale unei substanțe. În electrostatică și electrodinamică cvasi-staționară, mărimea este reală. Când se iau în considerare procesele oscilatorii de înaltă frecvență, faza de oscilație a vectorului și, prin urmare, a vectorului, poate să nu coincidă cu faza de oscilație a vectorului, în astfel de cazuri mărimea devine o mărime cu valoare complexă.
Să luăm în considerare întrebarea în ce condiții într-un mediu dielectric este posibilă apariția unei densități volumetrice necompensate a sarcinilor legate. În acest scop, scriem expresia pentru vectorul de polarizare în termeni de constantă dielectrică a mediului și vector:
A cărui validitate este ușor de verificat. Cantitatea de dobândă poate fi acum calculată:
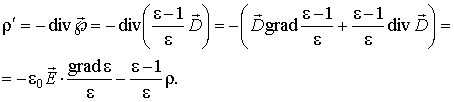 (3)
(3)
În absența unei densități volumetrice a sarcinilor libere într-un mediu dielectric, valoarea poate deveni zero dacă
a) câmpul lipsește; sau b) mediul este omogen sau c) vectorii și sunt ortogonali. În cazul general, este necesar să se calculeze valoarea utilizând relațiile (3).
Întrebarea nr. 17
 Să luăm în considerare comportamentul vectorilor EȘi D la interfata dintre doi dielectrici izotropi omogene cu permeabilitati si in absenta sarcinilor libere la interfata.
Să luăm în considerare comportamentul vectorilor EȘi D la interfata dintre doi dielectrici izotropi omogene cu permeabilitati si in absenta sarcinilor libere la interfata.
Condiții la limită pentru componentele normale ale vectorilor D și E rezultă din teorema lui Gauss. Să selectăm o suprafață închisă sub forma unui cilindru lângă interfață, a cărei generatoare este perpendiculară pe interfață, iar bazele sunt la o distanță egală de interfață.
Deoarece nu există încărcături libere la interfața dintre dielectrici, atunci, în conformitate cu teorema lui Gauss, fluxul vectorului de inducție electrică prin suprafata data
Izolarea curge prin bazele și suprafața laterală a cilindrului
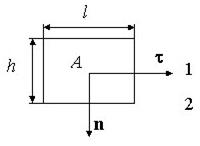 , unde este valoarea componentei tangente mediată pe suprafața laterală. Trecând la limita de la (în acest caz tinde și spre zero), obținem
, unde este valoarea componentei tangente mediată pe suprafața laterală. Trecând la limita de la (în acest caz tinde și spre zero), obținem ![]() , sau în sfârșit pentru componentele normale ale vectorului de inducție electrică. Pentru componentele normale ale vectorului intensitatea câmpului obținem
, sau în sfârșit pentru componentele normale ale vectorului de inducție electrică. Pentru componentele normale ale vectorului intensitatea câmpului obținem ![]() . Astfel, la trecerea prin interfața dintre mediile dielectrice, componenta normală a vectorului are de suferit decalaj, și componenta normală a vectorului continuu.
. Astfel, la trecerea prin interfața dintre mediile dielectrice, componenta normală a vectorului are de suferit decalaj, și componenta normală a vectorului continuu.
Condiții la limită pentru componentele tangente ale vectorilor D și E rezultă din relația care descrie circulația vectorului intensității câmpului electric. Să construim un contur dreptunghiular închis de lungime lângă interfață lși înălțimi h. Având în vedere că pentru câmpul electrostatic și înconjurând conturul în sensul acelor de ceasornic, să ne imaginăm circulația vectorului Eîn următoarea formă: ![]() ,
,
unde este valoarea medie E n pe laturile dreptunghiului. Trecand la limita la , obtinem pentru componentele tangentiale E .
Pentru componentele tangențiale ale vectorului de inducție electrică, condiția la limită are forma ![]()
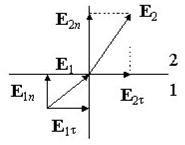 Astfel, la trecerea prin interfața dintre mediile dielectrice, componenta tangențială a vectorului continuu, iar componenta tangentă a vectorului are de suferit decalaj.
Astfel, la trecerea prin interfața dintre mediile dielectrice, componenta tangențială a vectorului continuu, iar componenta tangentă a vectorului are de suferit decalaj.
Refracția liniilor de câmp electric. Din condițiile la limită pentru vectorii componente corespunzători EȘi D rezultă că la traversarea interfeţei dintre două medii dielectrice, liniile acestor vectori sunt refractate (Fig. 2.8). Să extindem vectorii E 1Și E 2 la interfata in componente normale si tangentiale si determina relatia dintre unghiuri si in conditia . Este ușor de observat că aceeași lege de refracție a liniilor de tensiune și a liniilor de deplasare este valabilă atât pentru intensitatea câmpului, cât și pentru inducție.
![]() .
.
La trecerea la un mediu cu o valoare mai mică, unghiul format de liniile de tensiune (deplasare) cu normalul scade, prin urmare, liniile sunt localizate mai rar. Când treceți într-un mediu dintr-o linie mai mare de vectori EȘi D, dimpotrivă, sunt condensate şi îndepărtându-se de normal.
Întrebarea #6
Teorema privind unicitatea soluțiilor la problemele de electrostatică (dată fiind amplasarea conductorilor și sarcinile acestora).
Dacă este dată locația conductorilor în spațiu și sarcina totală a fiecăruia dintre conductori, atunci vectorul intensității câmpului electrostatic în fiecare punct este determinat într-un mod unic. Document: (prin contradicție)
Să fie repartizată sarcina de pe conductori după cum urmează:
Să presupunem că nu numai aceasta, ci și o distribuție a taxelor diferită de aceasta este posibilă:
(adică diferă cât se dorește pe cel puțin un conductor)
Aceasta înseamnă că cel puțin într-un punct din spațiu va fi găsit un alt vector E, adică. aproape de noi valori de densitate, cel puțin în unele puncte E va fi excelent. Acea. cu acelasi condiții inițiale, cu aceiași conductori obținem o soluție diferită. Acum să schimbăm semnul încărcăturii cu cel opus.
(semnul trebuie schimbat pe toți conductorii simultan)
În acest caz, aspectul liniilor de câmp nu se va modifica (nu contrazice nici teorema Gauss, nici teorema circulației), doar direcția și vectorul E se vor schimba.
Acum să luăm o suprapunere de taxe (o combinație de două opțiuni de încărcare):
(adică să punem o încărcare peste alta și să o încărcăm în al treilea mod)
Dacă nu coincide măcar undeva cu , atunci cel puțin într-un loc obținem câteva
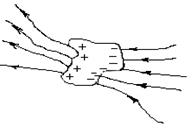 3) ducem liniile la infinit fără a le închide pe conductor. în acest caz închidem conturul închis L la infinit. Dar chiar și în acest caz, ocolirea linie de alimentare nu va da circulatie zero.
3) ducem liniile la infinit fără a le închide pe conductor. în acest caz închidem conturul închis L la infinit. Dar chiar și în acest caz, ocolirea linie de alimentare nu va da circulatie zero.
Concluzie: aceasta înseamnă că nu poate fi diferită de zero, ceea ce înseamnă că distribuția sarcinilor este stabilită într-un mod unic -> unicitatea soluției, i.e. E – îl găsim într-un mod unic.
Întrebarea nr. 7
Biletul 7. Teorema privind unicitatea soluțiilor la problemele de electrostatică. (se precizează locațiile conductoarelor și potențialele acestora). Dacă sunt date locația conductorilor și potențialul fiecăruia dintre ei, atunci intensitatea câmpului electrostatic în fiecare punct poate fi găsită într-un mod unic.
(curs Berkeley)
Peste tot în afara conductorului funcția trebuie să satisfacă ecuația cu diferență parțială: , sau, în caz contrar, (2)
Este evident că W nu îndeplinește condițiile la limită. La suprafața fiecărui conductor, funcția W este egală cu zero, deoarece iau aceeași valoare la suprafața conductorului. Prin urmare, W este o soluție la o altă problemă electrostatică, cu aceiași conductori, dar cu condiția ca toți conductorii să aibă potențial zero. Dacă este așa, atunci putem spune că funcția W este egală cu zero în toate punctele spațiului. Dacă nu este cazul, atunci trebuie să aibă undeva un maxim sau un minim. Calea W are un extremum în punctul P; apoi luați în considerare o minge cu centru în acest punct. Știm că valoarea medie pe sfera unei funcții care satisface ecuația lui Laplace este egală cu valoarea funcției din centru. Este nedrept dacă centrul este maxim sau minim al acestei funcții. Astfel, W nu poate avea un maxim sau un minim; trebuie să fie egal cu zero peste tot. Rezultă că =
Întrebarea nr. 28
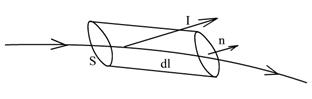 Trm. despre circulatie eu.
Trm. despre circulatie eu.
I este vectorul de magnetizare. I = = N p 1 m = N n i 1 S\c
DV = Sdl cosα; di mol = i 1 mol NSdl cosα = cIdl cosα, N este numărul de mol-l pe 1 cm 3. În apropierea conturului, considerăm substanța ca fiind omogenă, adică toți dipolii, toate moleculele au același moment magnetic. Pentru a calcula, să luăm o moleculă al cărei nucleu este situat direct pe conturul dl. Trebuie să numărăm câți atomi vor traversa cilindrul o dată => Aceștia sunt cei ai căror centre se află în interiorul acestui cilindru foarte imaginar. Astfel, ne interesează doar eu spun – adică. curent care traversează o suprafață susținută de un contur.
Întrebarea nr. 9
1. Energia unui sistem de sarcini punctuale staționare . Forțele electrostatice sunt conservatoare și sistemul de sarcini are energie potențială. Fie sarcinile Q 1 și Q 2 să fie la o distanță r una de cealaltă. Fiecare dintre aceste sarcini în câmpul celeilalte are energie potențială
unde φ 12 și φ 21 sunt, respectiv, potențialele create de sarcina Q 2 în punctul în care se află sarcina Q 1 și invers.
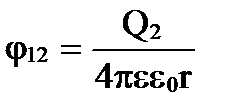 ;
; 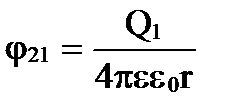 .
.
W 1 = W 2 =W = Q 1 φ 12 = Q 2 φ 21 = ½ (Q 1 φ 12 + Q 2 φ 21).
Adunând sarcini Q 3 , Q 4 , ..., Q n succesiv la un sistem de două sarcini, se poate verifica dacă energia de interacțiune a sistemului de sarcini este egală cu
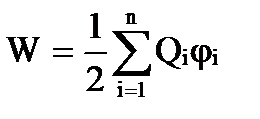 ,
,
unde φ i este potențialul creat în punctul în care sarcina Q i este localizată de toate sarcinile cu excepția celei i-a.
2. Energia unui conductor solitar încărcat . Să existe un conductor solitar a cărui sarcină, capacitate și potențial sunt Q, C, φ.
Să creștem taxa cu dQ. Pentru a face acest lucru, este necesar să transferați sarcina dQ de la infinit la suprafața conductorului, cheltuind muncă egală cu
dA = φdQ = C φd φ
Pentru a încărca un corp de la potențial zero la un potențial egal cu φ, trebuie să se lucreze
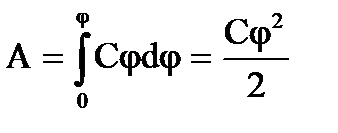
Energia conductorului încărcat va fi egală cu acest lucru

Având în vedere că  , această energie poate fi reprezentată sub formă
, această energie poate fi reprezentată sub formă
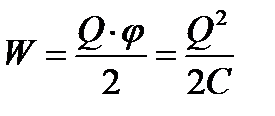
3. Energia unui condensator încărcat . Ca orice conductor încărcat, un condensator are energie
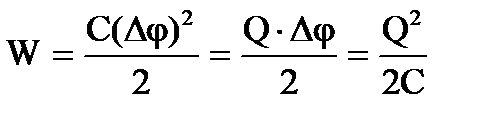
unde Q este sarcina condensatorului, C este capacitatea acestuia și Δφ este diferența de potențial dintre plăci.
Folosind expresia energiei, putem găsi forța mecanică (ponderomotivă) cu care plăcile condensatorului se atrag reciproc. Pentru a face acest lucru, presupuneți că distanța x dintre plăci se modifică cu cantitatea dx. Apoi forță efectivă functioneaza egal cu
datorita scaderii energiei potentiale Fdx = - dW, de unde
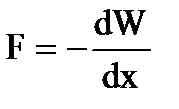 .
.
Înlocuirea energiei în formulă 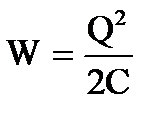 exprimarea capacității
exprimarea capacității
 , primim
, primim
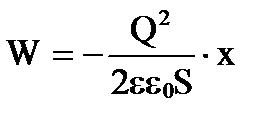 .
.
Diferențierea W în raport cu X, să găsim forța F
 ,
,
unde semnul minus indică faptul că forța F tinde să reducă distanța dintre plăci, i.e. este forța de atracție. Înlocuind expresia pentru densitatea de sarcină pe plăci  , primim
, primim 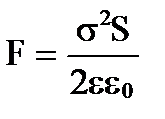 .
.
Având în vedere intensitatea câmpului că E =  , primim
, primim
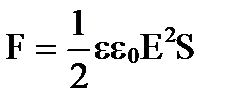 .
.
Presiunea pe plăcile dielectrice plasate în golul condensatorului va fi
![]()
4. Energia câmpului electrostatic.
Să transformăm formula pentru energia unui condensator plat  , folosind formule
, folosind formule
 și Δφ = Ed.
și Δφ = Ed.
Primim,
unde V este volumul spațiului dintre plăcile condensatorului în care este concentrată energia câmpului său W.
Densitatea de energie a câmpului volumetric w este energia conținută într-o unitate de volum a câmpului electric și este egală cu
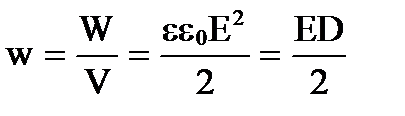 .
.
Unitate de măsură [J/m3].
Se poate observa că densitatea de energie a câmpului volumetric depinde doar de caracteristicile câmpului și ale mediului.

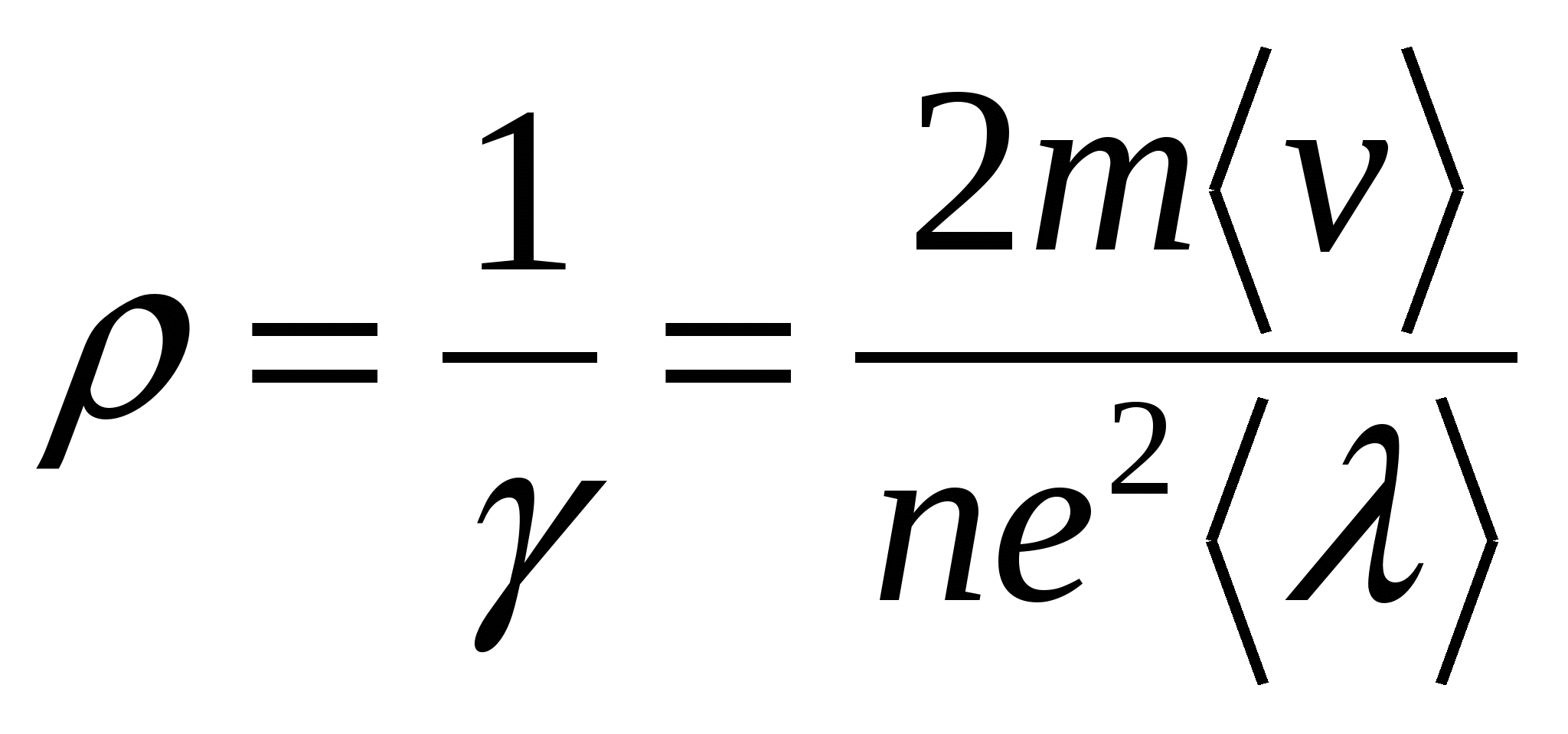 .
. . Electronul transferă complet această energie ionului rețelei cristaline la ciocnirea cu acesta. Multe astfel de ciocniri au ca rezultat eliberarea de căldură Joule. Dacă concentraţia de electroni n, iar fiecare dintre ele se confruntă
. Electronul transferă complet această energie ionului rețelei cristaline la ciocnirea cu acesta. Multe astfel de ciocniri au ca rezultat eliberarea de căldură Joule. Dacă concentraţia de electroni n, iar fiecare dintre ele se confruntă  ori în 1 s, atunci puterea va fi eliberată într-o unitate de volum a conductorului
ori în 1 s, atunci puterea va fi eliberată într-o unitate de volum a conductorului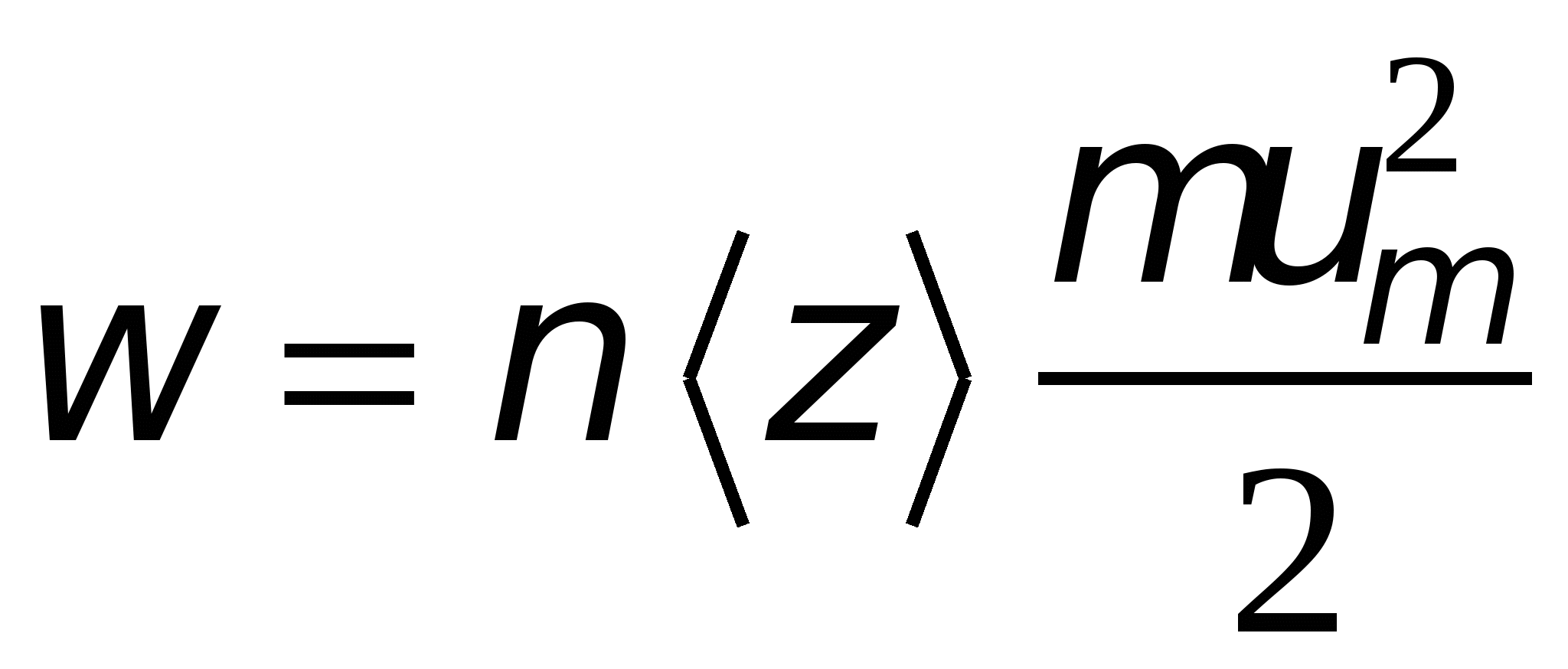 .
.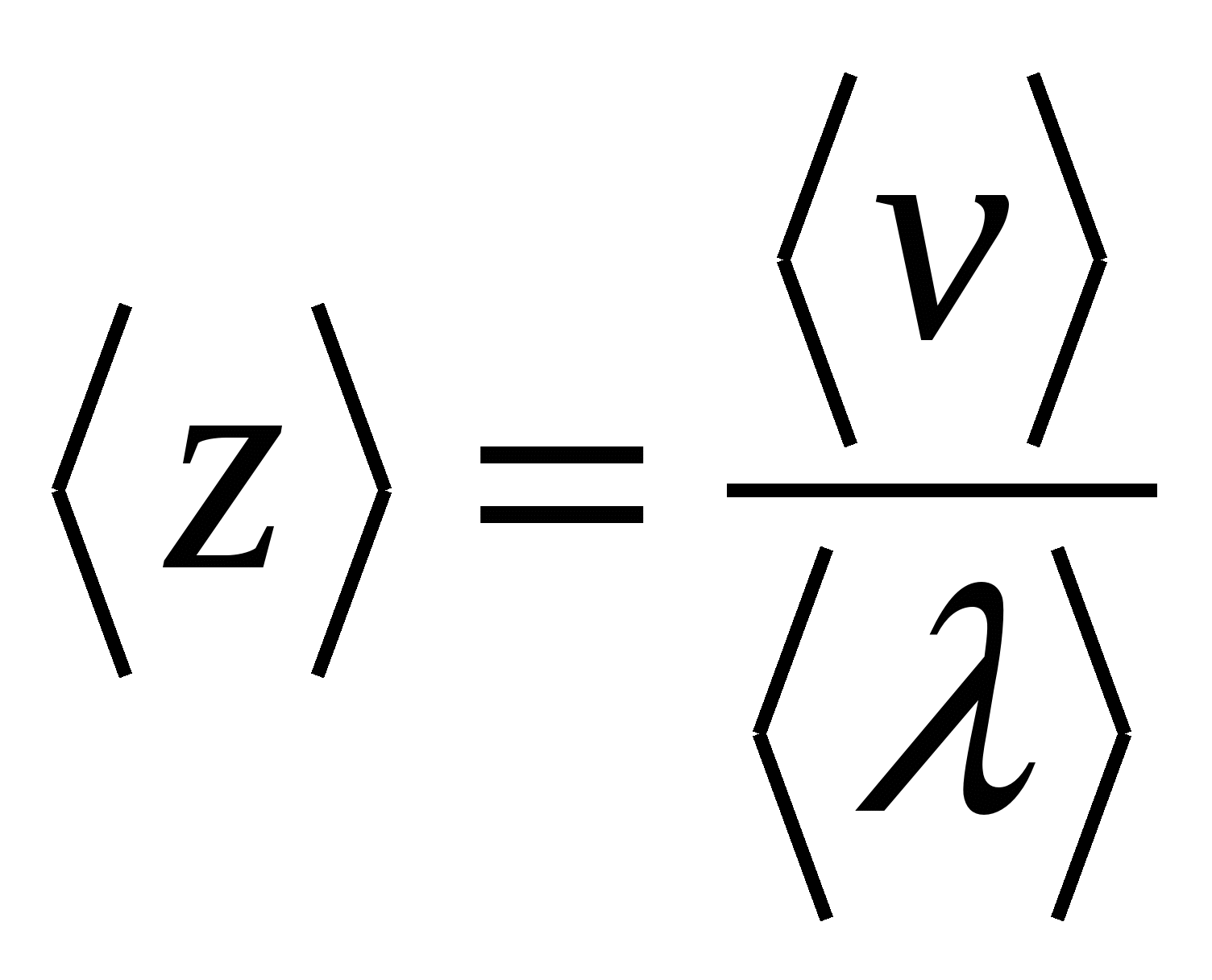 ,
, 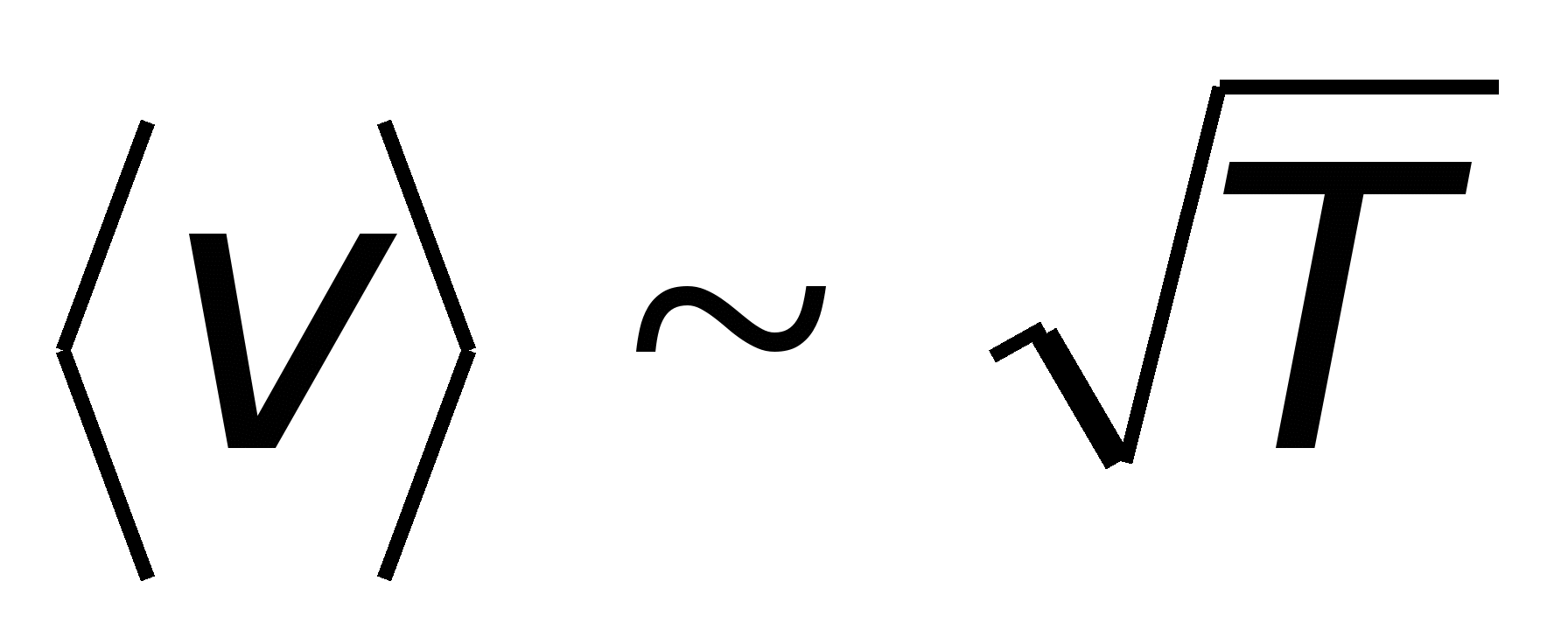 , prin urmare, rezistivitate
, prin urmare, rezistivitate 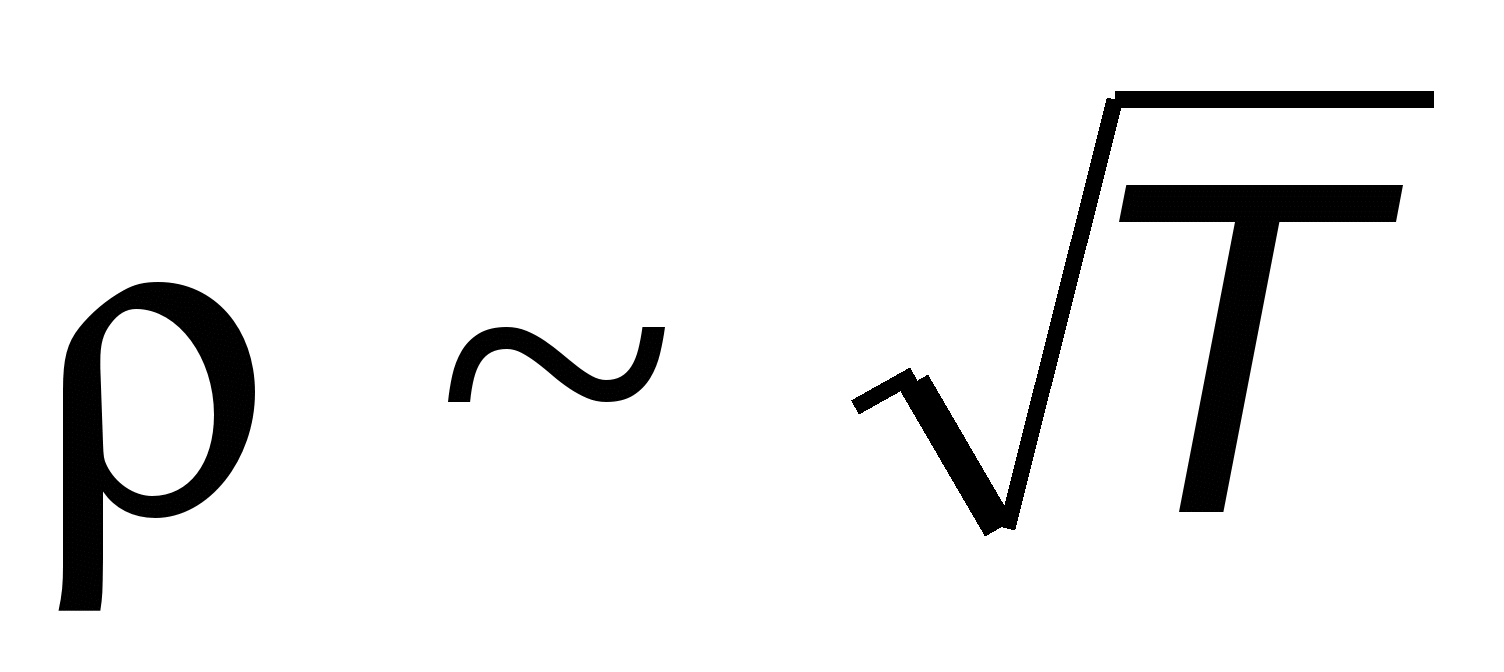 . Între timp, experiența arată că depinde liniar de temperatură
. Între timp, experiența arată că depinde liniar de temperatură 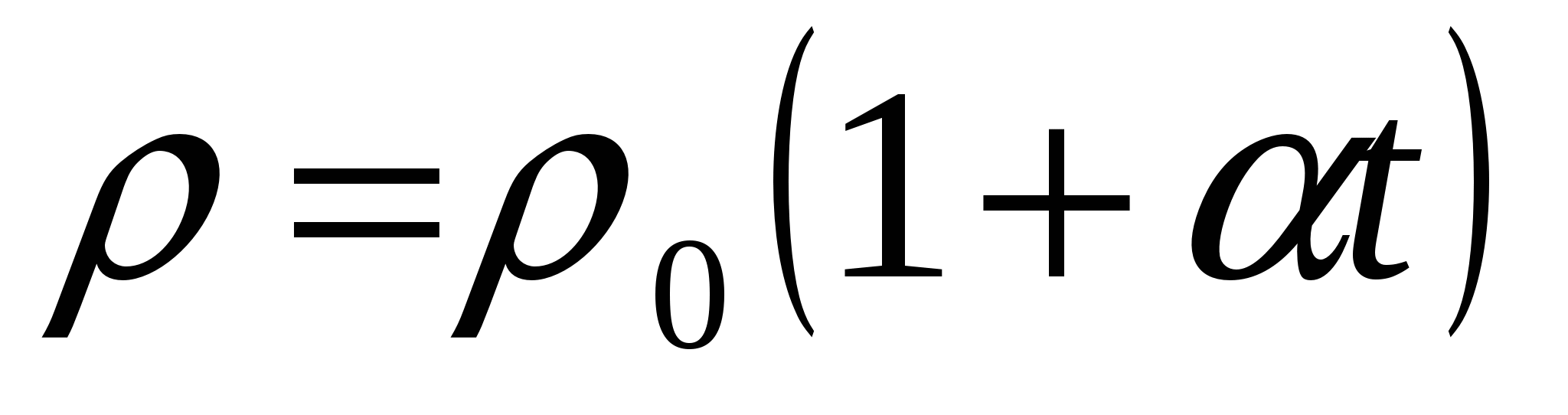 ,
,
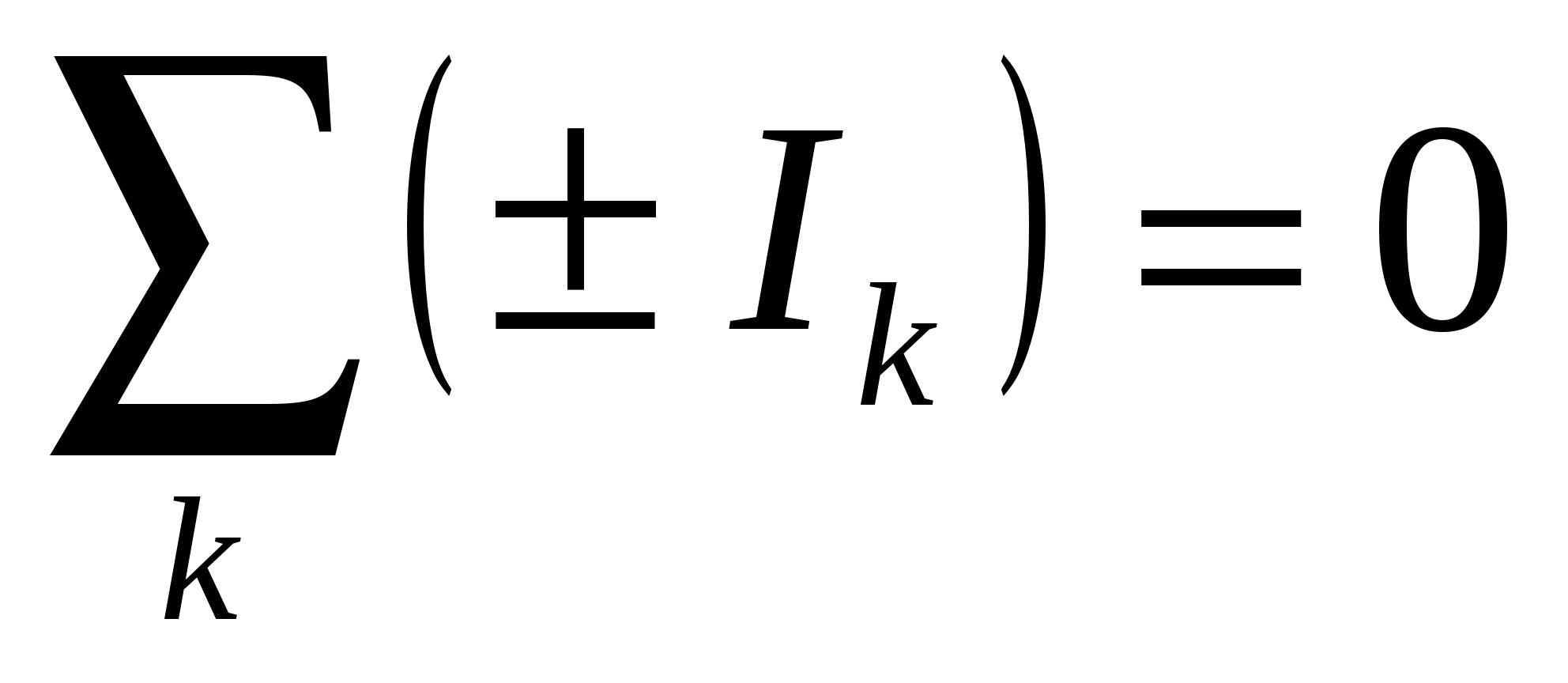 .
.
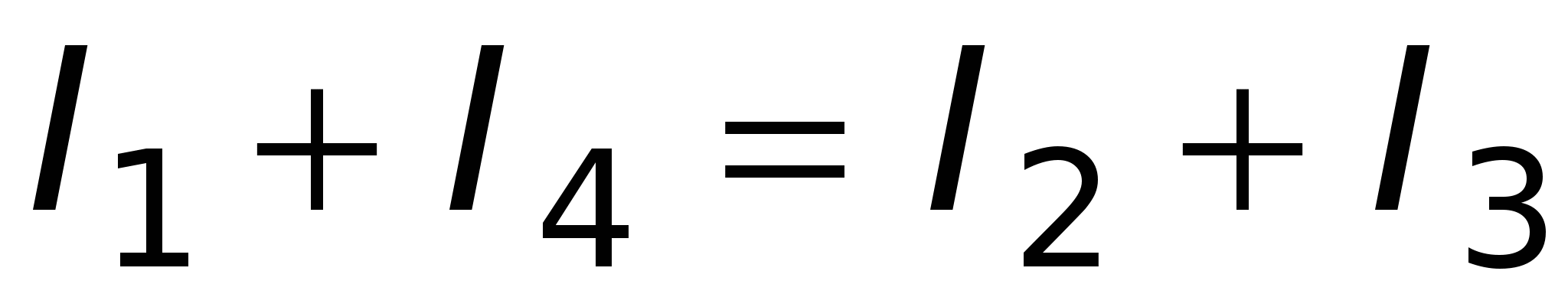 ,
,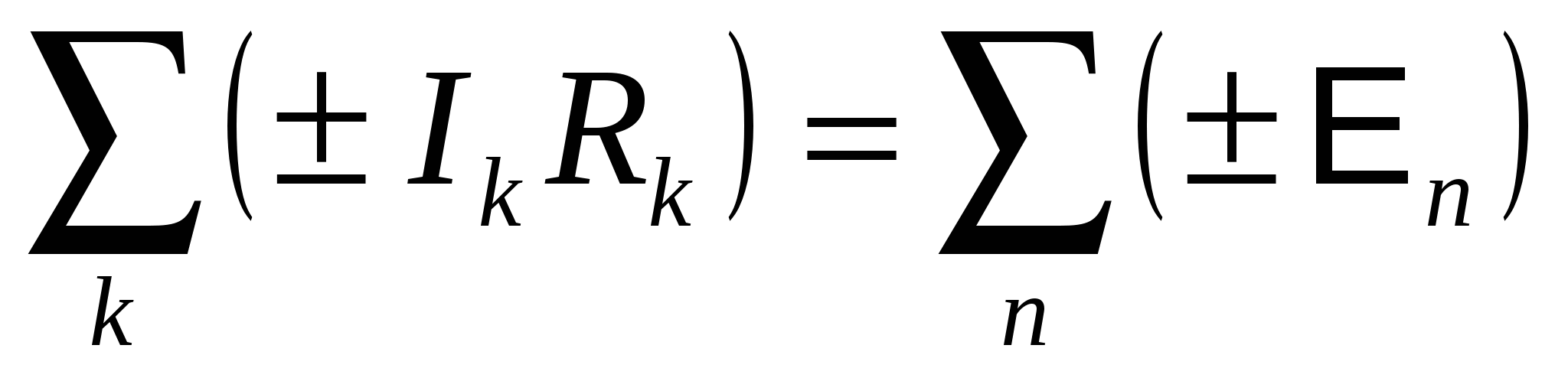 .
.