Объемная плотность энергии электрического поля
14.1. Энергия системы точечных зарядов
Рис. 14.1
Из сопоставления (14.1) и (14.2) видно, что Q 1 Q 2 , поэтому энергию системы из двух точечных зарядов можно представить в симметричном виде:
где i – потенциал поля, создаваемого всеми зарядами, кроме i -го, в точке, где расположен i -ый заряд.
^
14.2. Энергия заряженного проводника
Заряд, расположенный на поверхности проводника, можно рассматривать как систему точечных зарядов, поэтому для вычисления энергии заряженного проводника можно воспользоваться формулой (14.4). Потенциал любой точки поверхности проводника одинаков ( i =), поскольку его поверхность эквипотенциальна. Следовательно, в формуле (14.4) потенциал можно вынести за знак суммы:
 или
или  , (14.5) где
, (14.5) где 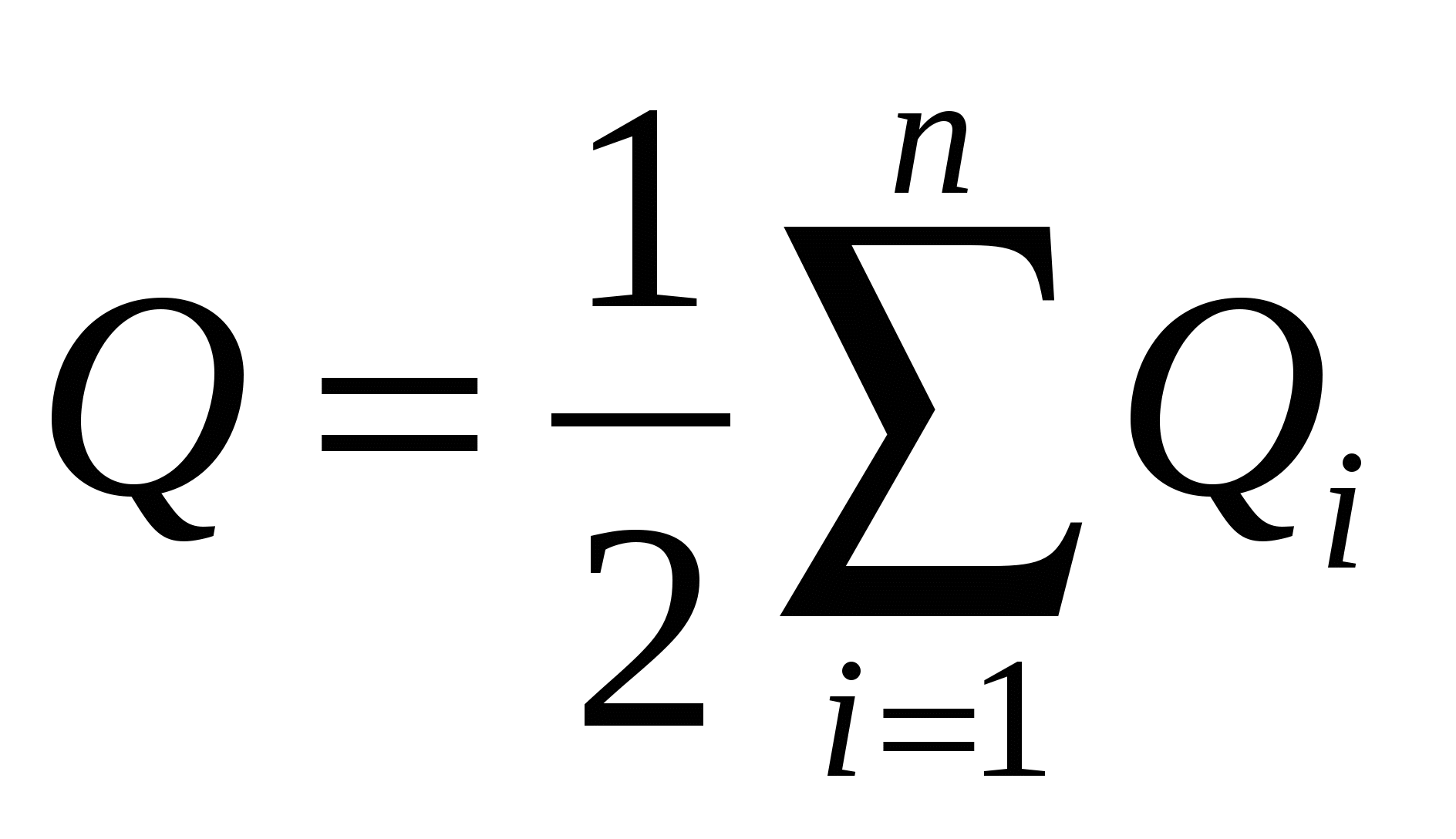 – заряд проводника.
– заряд проводника.
С учётом (13.3) выражение для энергии заряженного проводника можно представить в виде
^
14.3. Энергия заряженного конденсатора. Плотность энергии электростатического поля
Для вычисления энергии заряженного конденсатора воспользуемся формулами (14.5) – (14.7), заменив на разность потенциалов между обкладками конденсатора U=
. Тогда
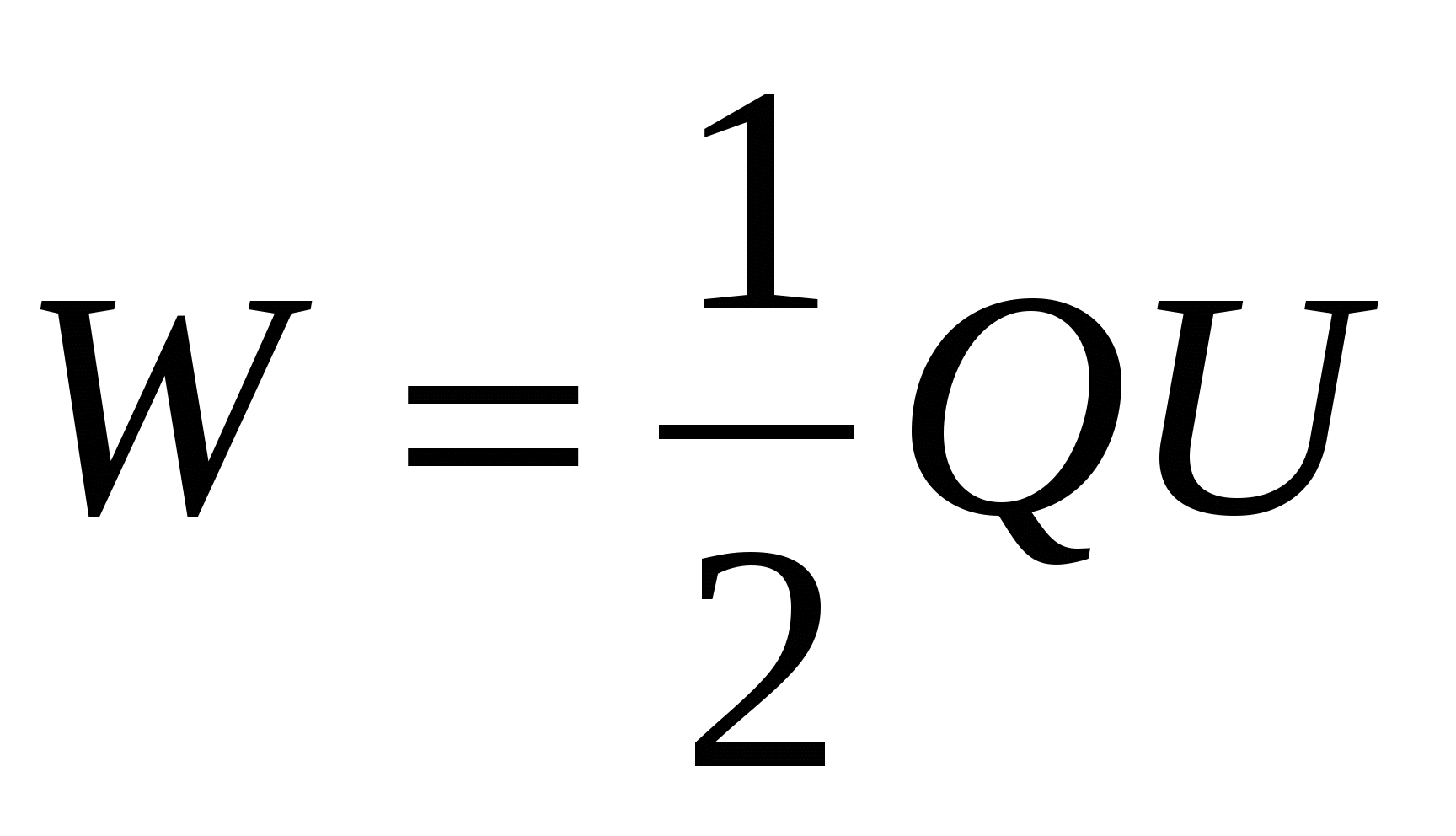 , , | (14.8) |
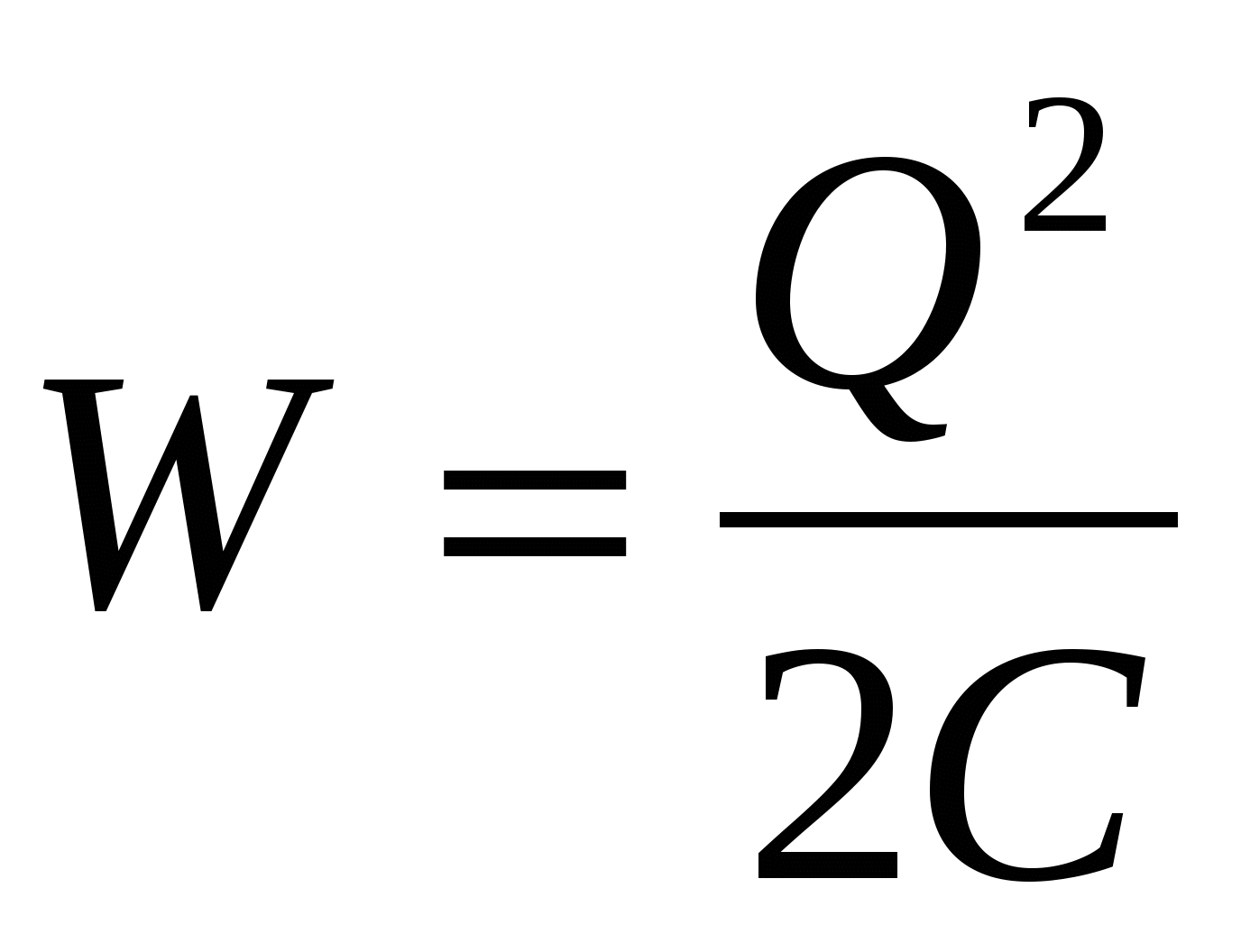 | (14.9) |
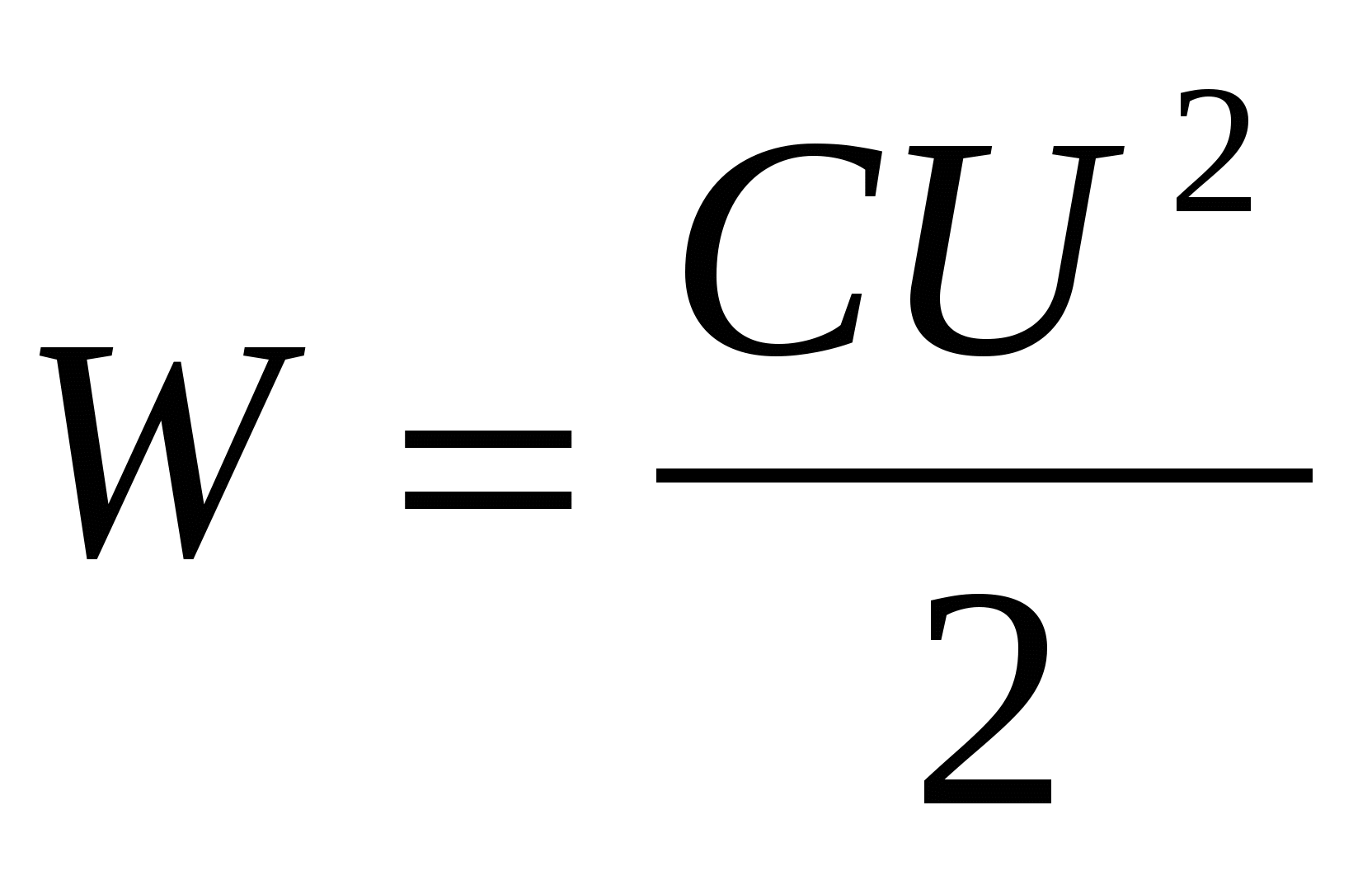 | (14.10) |
Дальнейшее рассмотрение проведём, основываясь на формуле (14.9). Представим заряд конденсатора как Q= S , где – поверхностная плотность заряда, а S – площадь обкладки конденсатора. Воспользовавшись далее выражением для ёмкости плоского конденсатора (13.7), представим (14.9) в виде
В формуле (14.9) энергия заряженного конденсатора выражена через заряд на его обкладках и ёмкость. В формуле (14.12) энергия конденсатора выражена через напряжённость электростатического поля, сосредоточенного между его обкладками. В связи с этим возникает принципиальный вопрос о том, что служит носителем энергии конденсатора: заряды или электростатическое поле. Этот вопрос – центральный в длительной дискуссии между сторонниками дальнодействия и близкодействия.
Сторонники дальнодействия отдавали предпочтение формуле (14.9), рассматривая её как потенциальную энергию взаимодействия двух тел. Приверженцы этой теории отвергали возможность осуществления взаимодействия посредством поля.
Сторонники теории близкодействия (полевой теории) считали, что энергия конденсатора есть энергия электростатического поля (формула (14.2)). Эта энергия "размазана" по всему объёму конденсатора и, следовательно, можно говорить об объёмной плотности энергии:
 [Дж/м 3 ] или
[Дж/м 3 ] или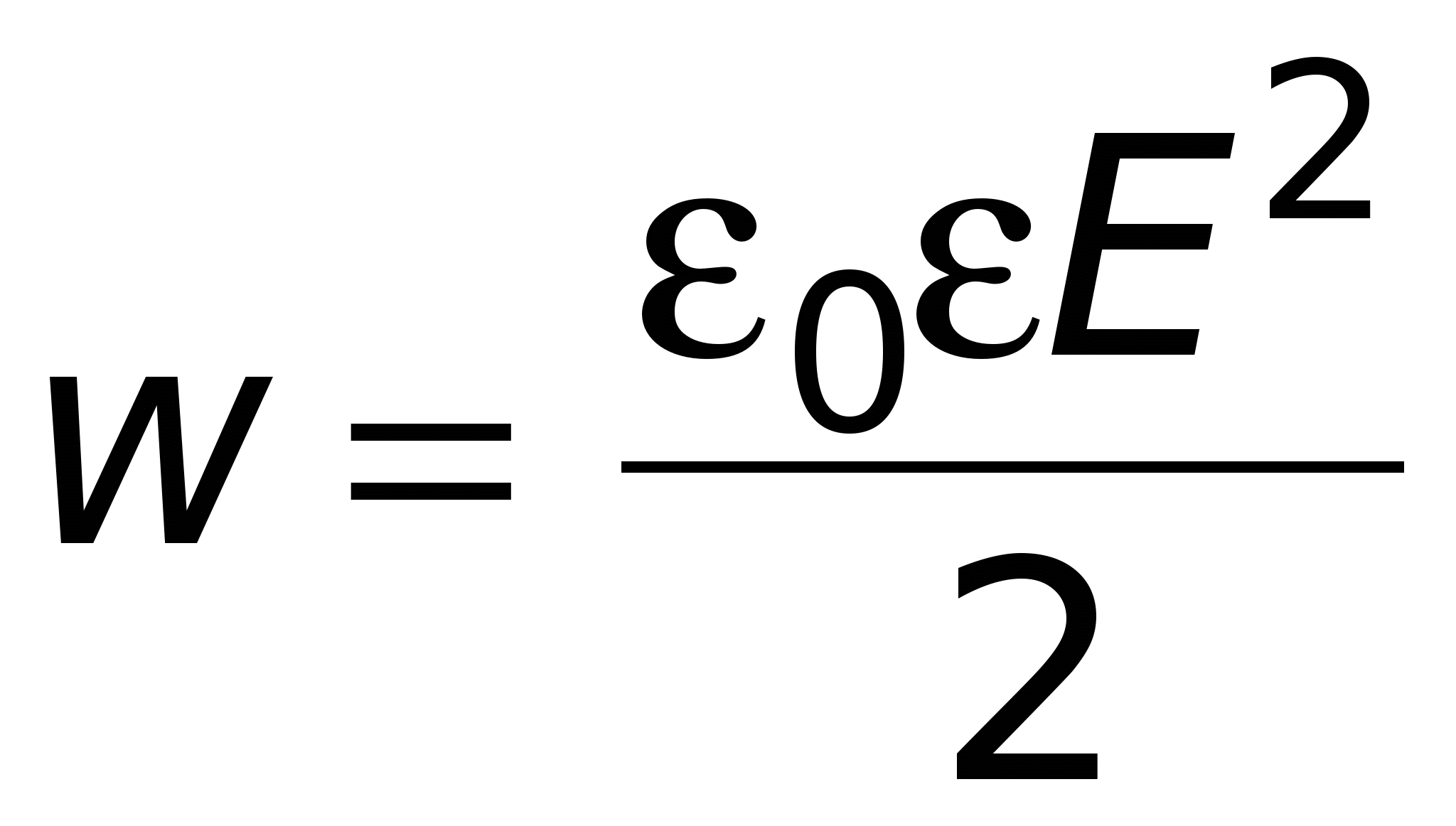 , С учётом (12.11) формулу (14.13) можно представить в виде
, С учётом (12.11) формулу (14.13) можно представить в виде
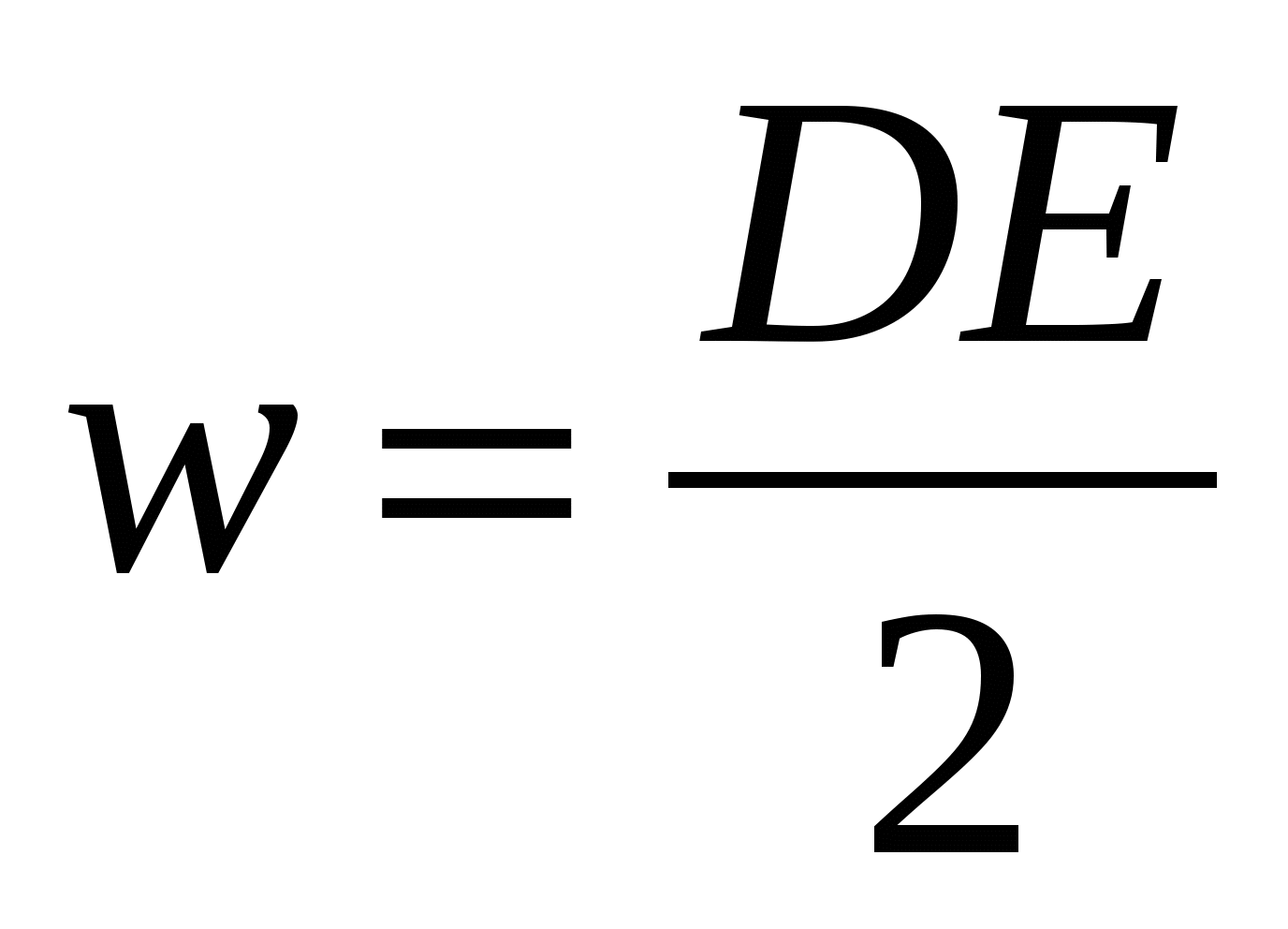 | (14.14) |
В рамках электростатики решить вопрос, что является носителем энергии – заряды или поле, невозможно, поскольку неподвижные заряды и создаваемое ими электростатическое поле неотделимы друг от друга. При изучении переменных электрических и магнитных полей оказалось, что электромагнитное поле может отрываться от зарядов, существуя независимо от них. Это и есть решающий аргумент в пользу теории близкодействия (полевой теории).
Лекція 23.
15. Постоянный электрический ток
^
15.1. Сила и плотность тока
Электрическим током называют упорядоченное (направленное) движение заряженных микрочастиц или заряженных макроскопических тел. За направление тока принимают направление движения положительных зарядов; если ток создается отрицательно заряженными частицами (например, электронами), то направление тока противоположно направлению движения частиц. Различают ток проводимости (направленное движение заряженных частиц внутри макроскопического тела) и конвекционный (движение заряженного тела как целого). В дальнейшем будем рассматривать лишь ток проводимости.
Количественно электрический ток характеризуется скалярной величиной силой тока I
и векторной величиной – плотностью электрического тока 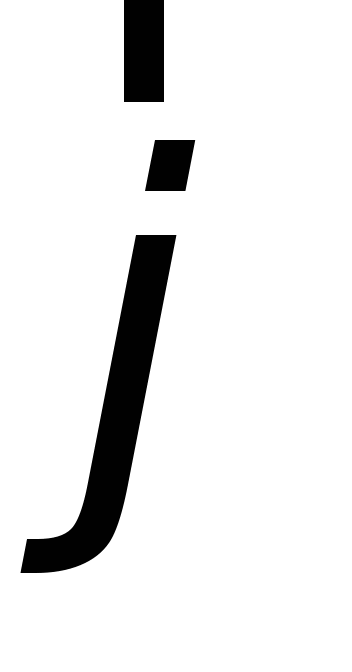 .
.
Сила тока численно равна заряду, прошедшему через поперечное сечение проводника за единицу времени:
где знак "" обозначает, что площадка 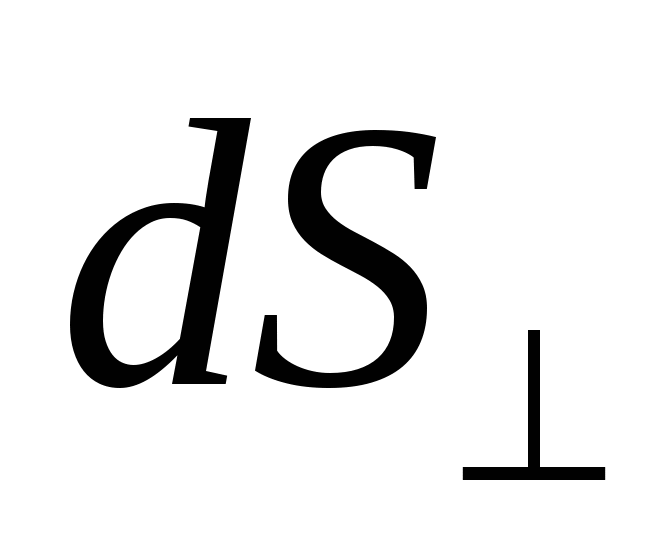 ориентирована перпендикулярно к направлению тока. Направление вектора
совпадает с направлением движения положительных зарядов.
ориентирована перпендикулярно к направлению тока. Направление вектора
совпадает с направлением движения положительных зарядов.
Найдем выражение для вектора плотности тока в металлах, у которых носителями тока являются свободные электроны. Под действием электрического поля электроны в металле движутся направлено со средней скоростью 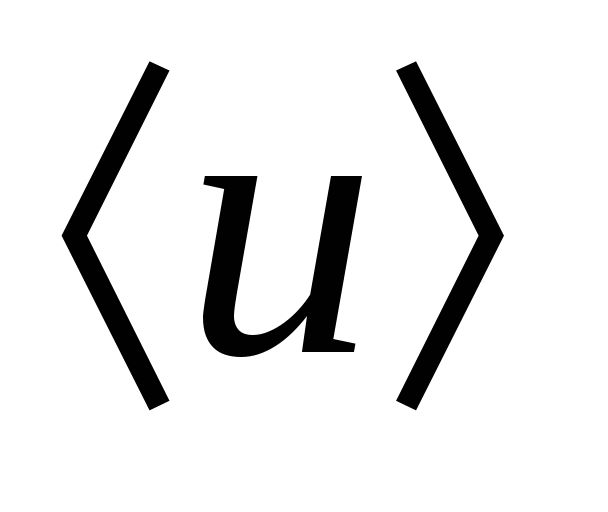 . За единицу времени через единичную площадку поперечного сечения проводника пройдет n
электронов, где n
– число электронов в единице объема (концентрация). При этом будет перенесен заряд en
. Следовательно плотность тока
. За единицу времени через единичную площадку поперечного сечения проводника пройдет n
электронов, где n
– число электронов в единице объема (концентрация). При этом будет перенесен заряд en
. Следовательно плотность тока
 . . | (15.3) |
15.2. Условия существования тока. Сторонние силы. ЭДС
Если вектор плотности тока не изменяется с течением времени ни по величине, ни по направлению, то такой ток называется постоянным. Найдем условия существования постоянного тока.

Рис. 15.1
Предположим, что на концах проводника создана разность потенциалов  , причем
, причем 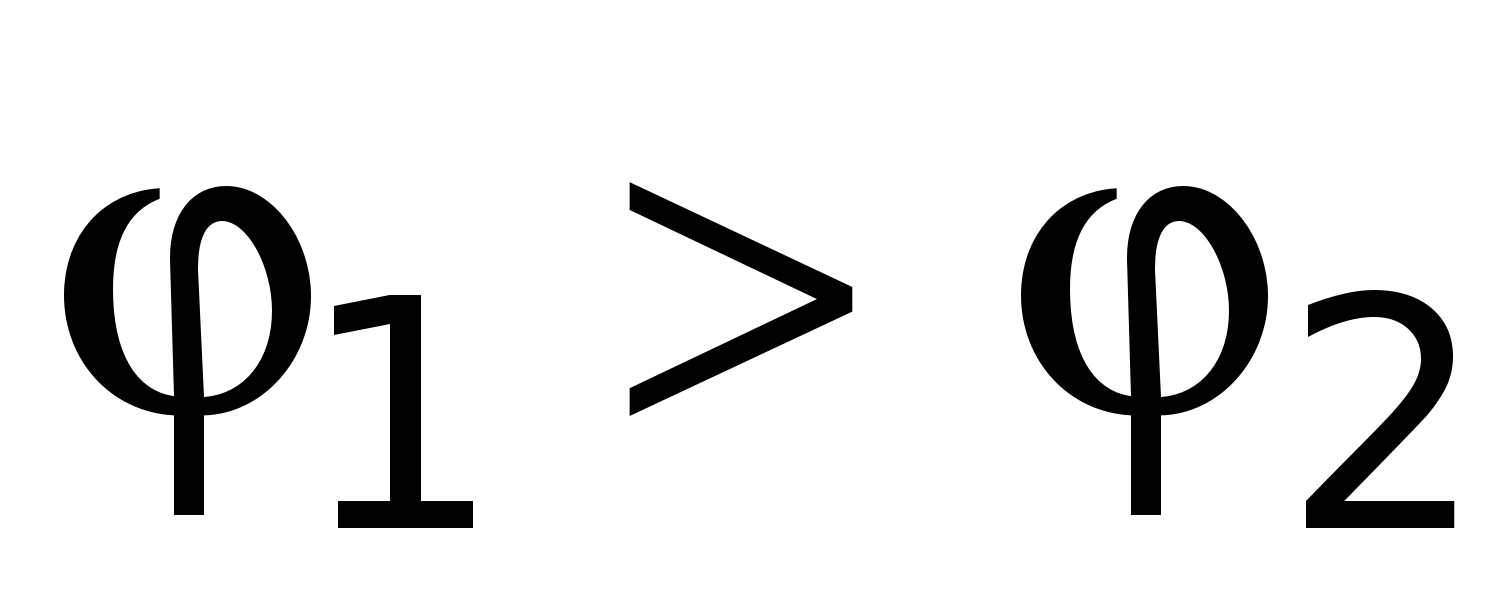 (рис. 15.1). При этом в проводнике возникнет кратковременный ток, вызванный упорядоченным движением зарядов в сторону убыли потенциала (предполагается, что носители тока имеют положительный заряд). Ток будет существовать до тех пор, пока не произойдет выравнивание потенциалов на концах проводника, Для того же, чтобы ток сохранялся постоянным в течение длительного времени, необходимо от конца проводника с меньшим потенциалом отводить заряды к концу проводника с большим потенциалом, т.е. осуществлять кругооборот зарядов. В связи с этим цепь должна быть замкнутой.
(рис. 15.1). При этом в проводнике возникнет кратковременный ток, вызванный упорядоченным движением зарядов в сторону убыли потенциала (предполагается, что носители тока имеют положительный заряд). Ток будет существовать до тех пор, пока не произойдет выравнивание потенциалов на концах проводника, Для того же, чтобы ток сохранялся постоянным в течение длительного времени, необходимо от конца проводника с меньшим потенциалом отводить заряды к концу проводника с большим потенциалом, т.е. осуществлять кругооборот зарядов. В связи с этим цепь должна быть замкнутой.
Электростатические силы такой кругооборот зарядов обеспечить не могут, так как на участке цепи, показанном на рис. 15.1 пунктиром, нужно выполнять работу против электростатического поля. Перемещение зарядов в сторону возрастания потенциала возможно лишь с помощью дополнительных сил неэлектростатического происхождения, называемых сторонними силами. Эти силы могут быть обеспечены химическими процессами (гальванические элементы), вихревым электрическим полем (генераторы переменного или постоянного тока) и т.д.
В отличие от электростатических сил, работа сторонних сил по перемещению заряда по замкнутому кругу отлична от нуля. Электродвижущей силой (ЭДС) называется работа, совершаемая сторонними силами по перемещению единичного положительного заряда по всей цепи, 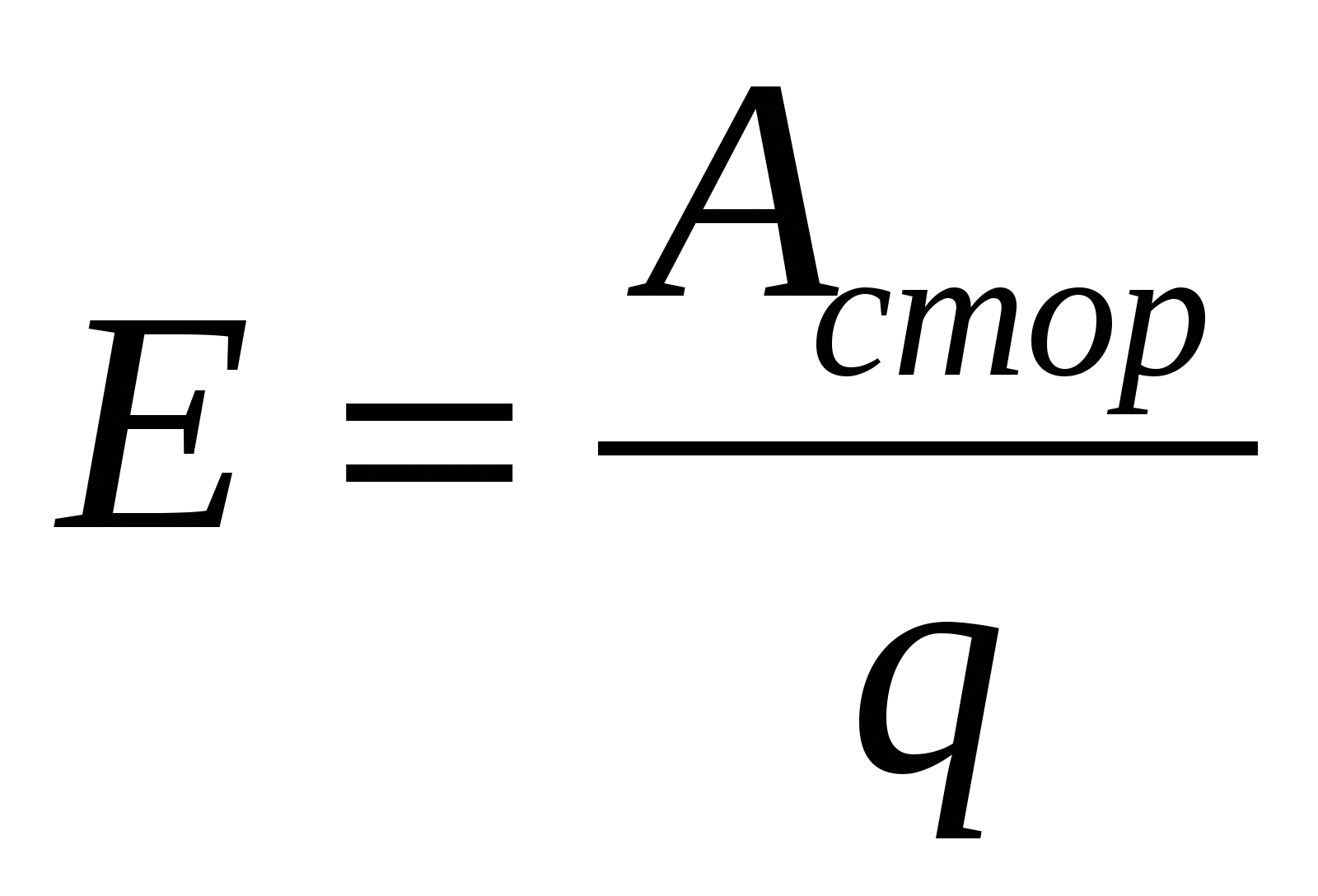 , (15.4) .Как и разность потенциалов, ЭДС измеряется в вольтах.
, (15.4) .Как и разность потенциалов, ЭДС измеряется в вольтах.
Рассмотрим участок цепи, на котором кроме сторонних сил действуют электростатические. Тогда работа по перемещению заряда на этом участке будет равна сумме работ: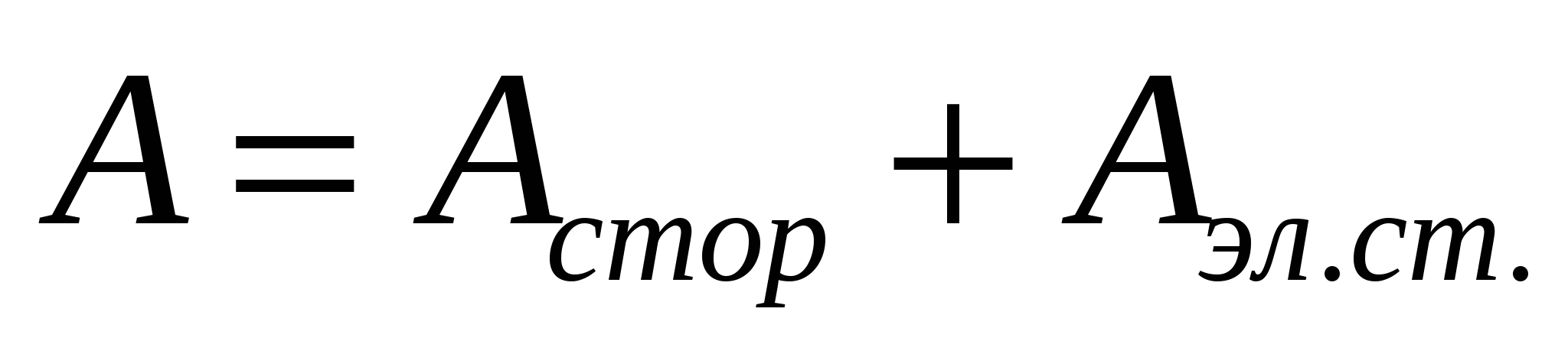
Разделим это выражение на заряд q
:
Суммарная работа, выполняемая как сторонними, так и электростатическими силами по перемещению единичного положительного заряда на некотором участке цепи, называется напряжением или падением напряжения:
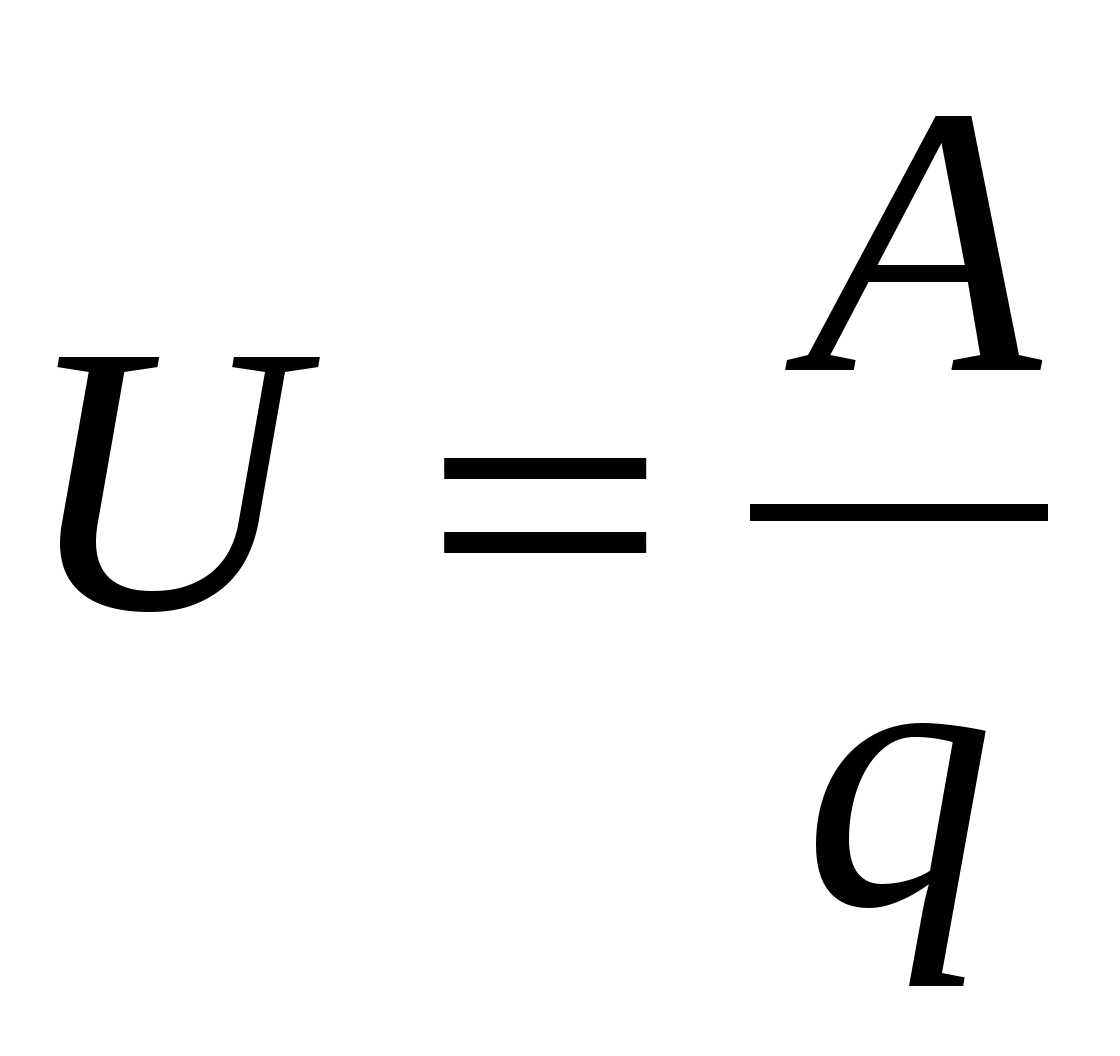 . . | (15.7) |
Подставив (15.4), (15.6) и (15.7) в (15.5), получим связь между напряжением, ЭДС и разностью потенциалов U=E + ( 1 - 2 )
Из (15.8) видно, что напряжение U
равно алгебраической сумме ЭДС и разности потенциалов на данном участке цепи.
^
15.3. Закон Ома
15.3.1. Закон Ома для неоднородного участка цепи
Ом экспериментально установил, что сила тока на некотором участке цепи пропорциональна напряжению и обратно пропорциональна сопротивлению: 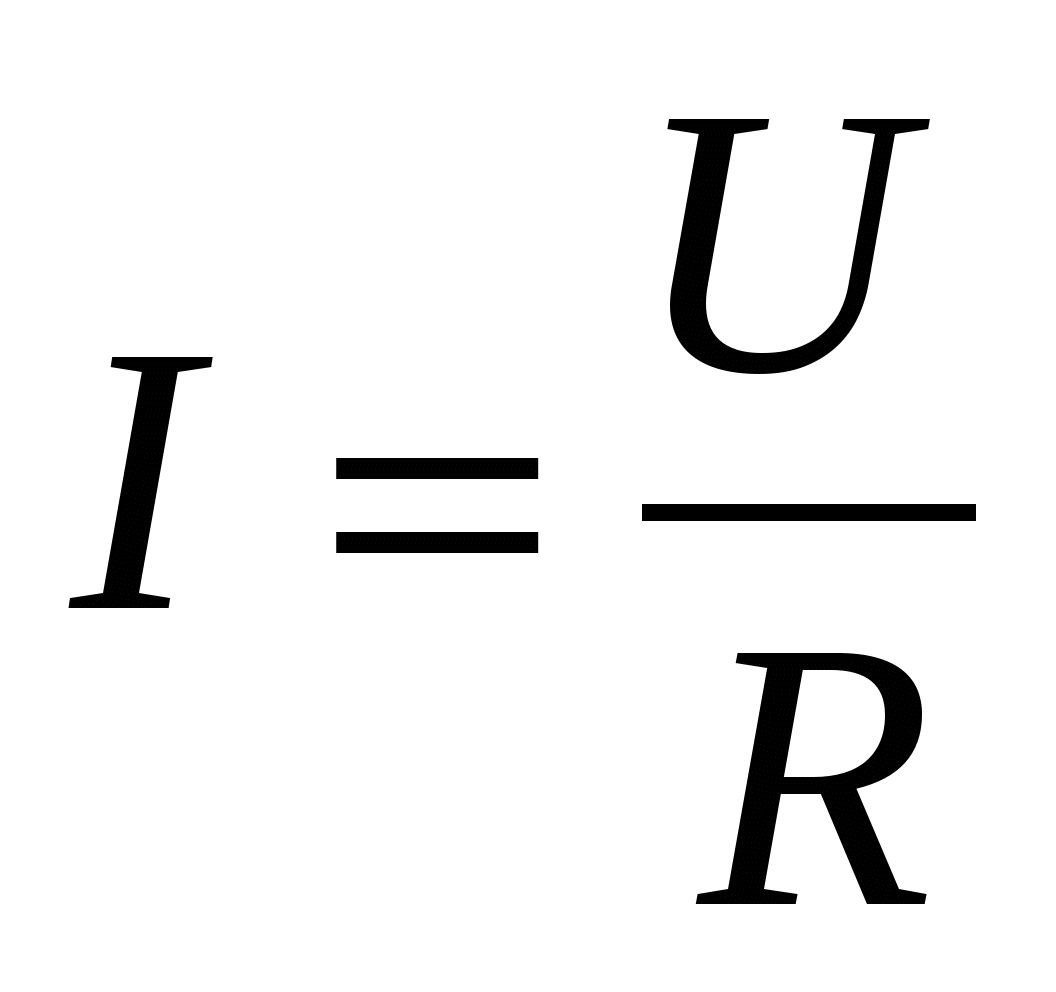 . . | (15.9) |
Найдем из (15.9) напряжение U и подставим в (15.8): IR = E +( 1 – 2 ) , (15.10)
Полученное выражение есть закон Ома для неоднородного участка цепи, т.е. участка цепи, содержащего ЭДС.

Рис. 15.2
При практическом использовании формулы (15.10) нужно установить знаки для напряжения и ЭДС. Для этого произвольным образом устанавливаем направление обхода (на рис. 15.2 направление обхода выбрано по часовой стрелке). Если направление тока совпадает с направлением обхода, то он берется со знаком "+", в противном случае его нужно взять со знаком "-". На рис. 15.2 направление обхода и направление тока не совпадают, поэтому в формуле (15.10) IR
берем со знаком "минус".
Остальная часть замкнутого контура на рис. 15.2 показана пунктиром. ЭДС по внешней цепи "перегоняет" заряды от своего "плюса" к "минусу". Ее нужно брать со знаком "+", если она действует в направлении обхода и со знаком "–" в противном случае. В соответствии с этим на схеме, изображенной на рис. 15.2, ЭДС нужно взять со знаком "+". Таким образом, закон Ома для неоднородного участка цепи в данном случае запишем в виде: –
IR
=
E
+(
1
–
2
)
.
^
15.3.2. Закон Ома для полной цепи
При обходе полной цепи начальная и конечная точки совпадают, поэтому 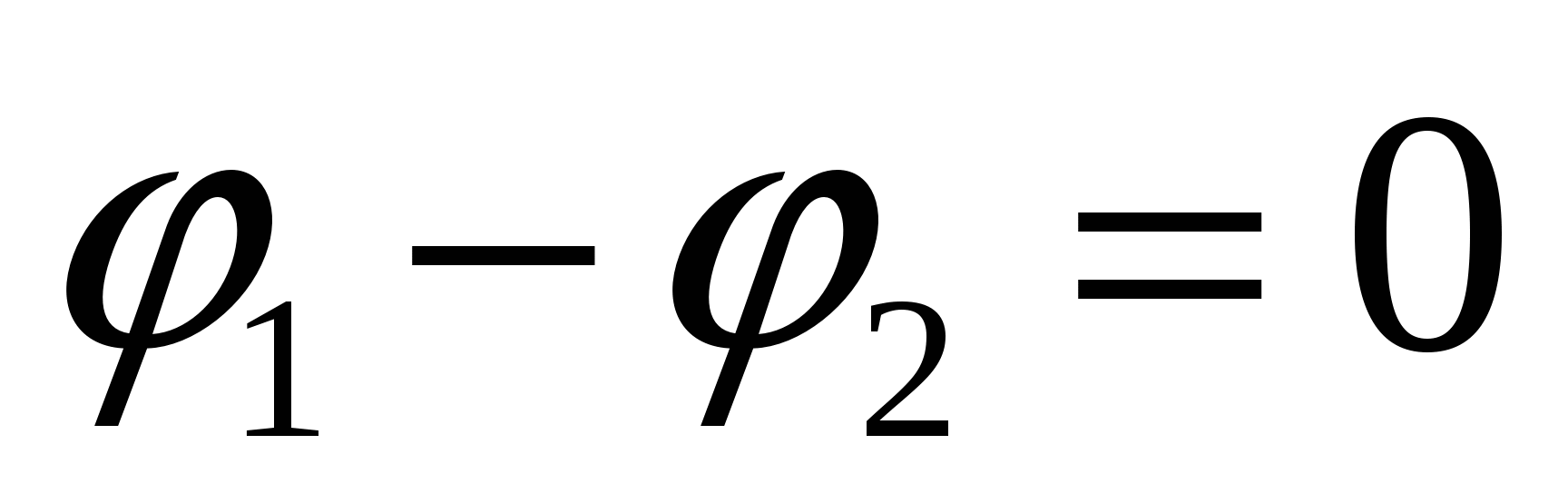 ;
;
^
15.3.3. Закон Ома для однородного участка цепи
Однородным называется участок цепи, не содержащий источника ЭДС, т.е. в формуле (15.10) нужно положить E
=0
. Тогда 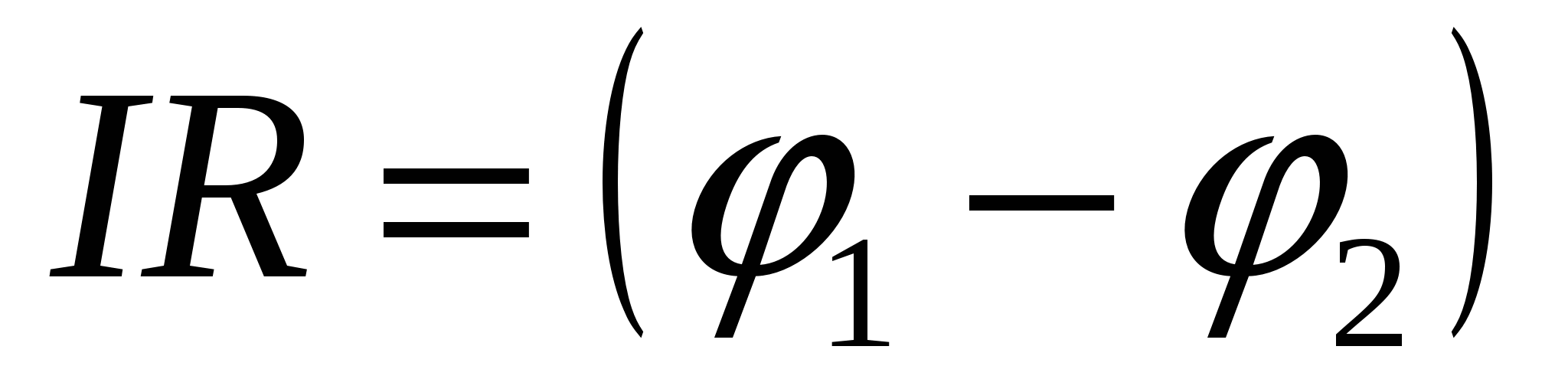 .
.
В данном случае падение напряжения совпадает с разностью потенциалов U
= 1 - 1 , т. е.
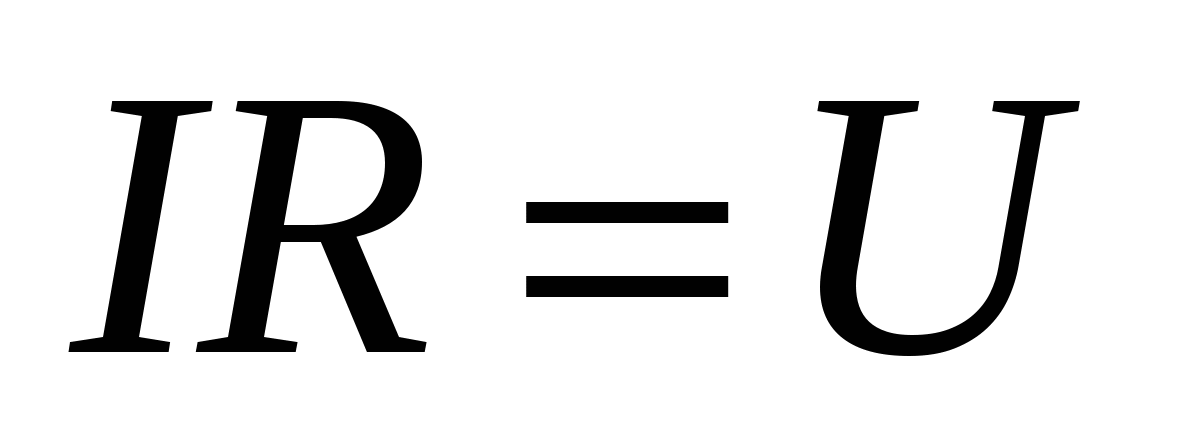 , , | (15.13) |
что также совпадает с (15.9).
Формулы (15.9) и (15.13) представляют закон Ома в интегральной форме.
^
15.3.4. Закон Ома в дифференциальной форме
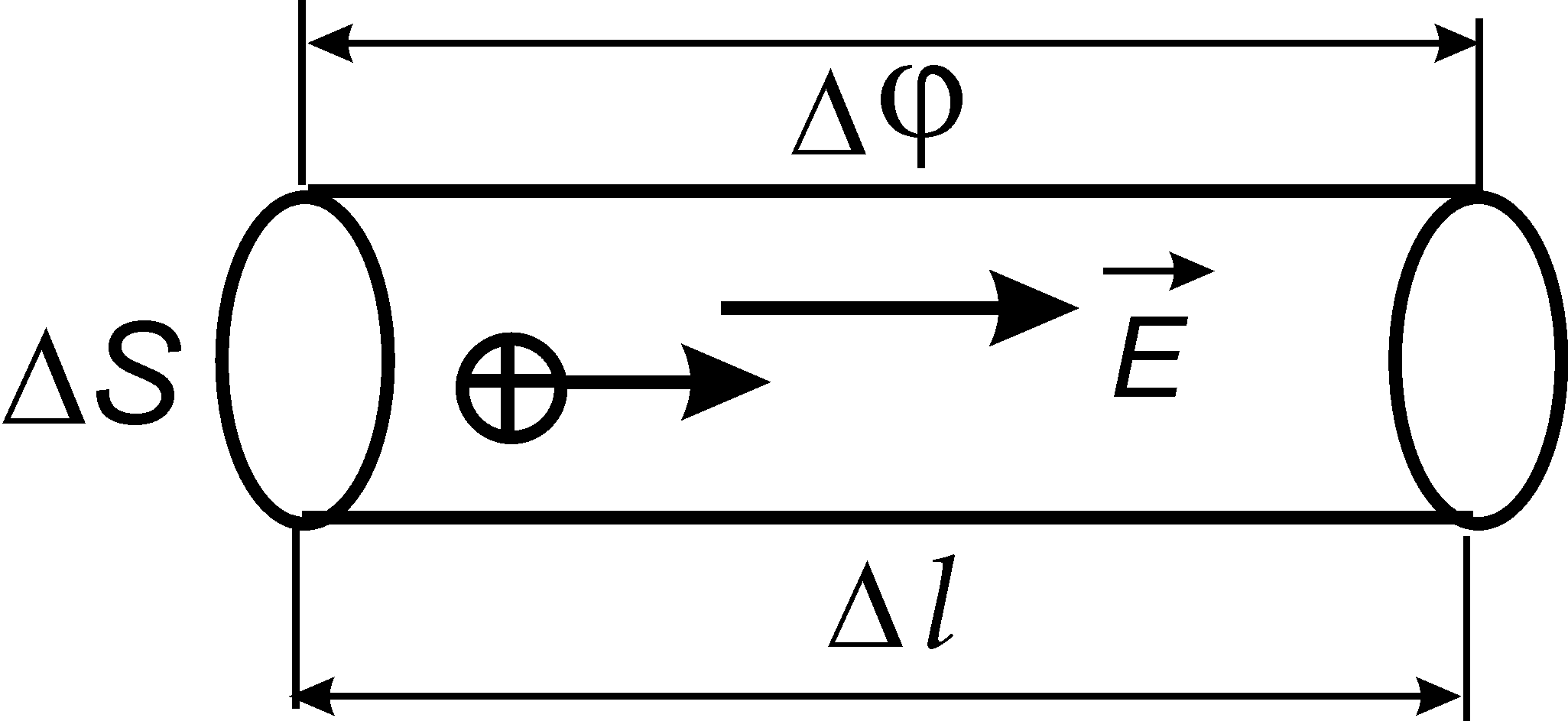
Рис. 5.3
Выделим внутри проводника с током элементарный цилиндр сечением S
и длиной l
(рис. 15.3). Сила тока в нем I
=S
, а его сопротивление  , где – удельное сопротивление проводника. Разность потенциалов на концах цилиндра . Тогда закон Ома (см. (15.9)) запишем в виде
, где – удельное сопротивление проводника. Разность потенциалов на концах цилиндра . Тогда закон Ома (см. (15.9)) запишем в виде
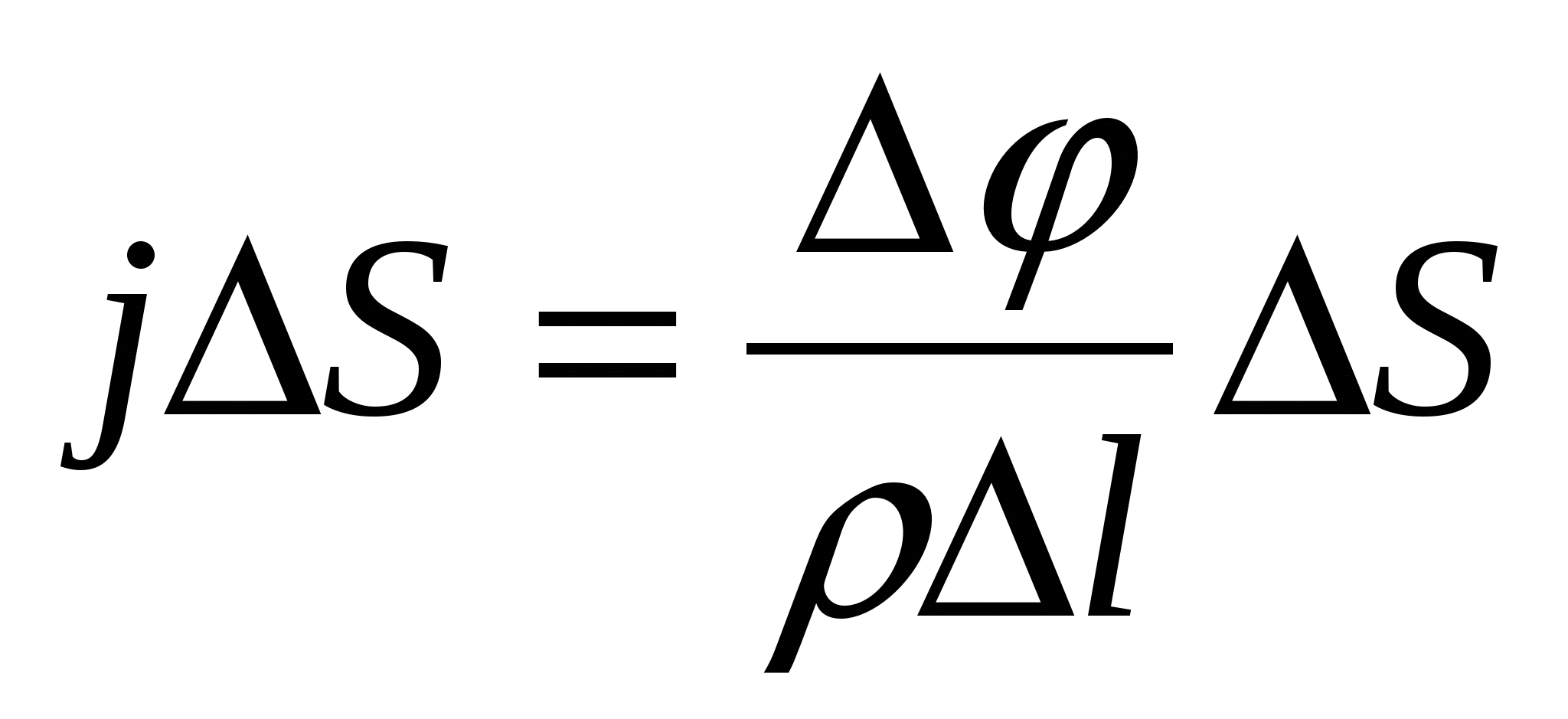 или .
или .
С учетом (11.30) последнее выражение можно преобразовать к виду
 . . | (15.14) |
Величина, обратная удельному сопротивлению, называется удельной проводимостью:
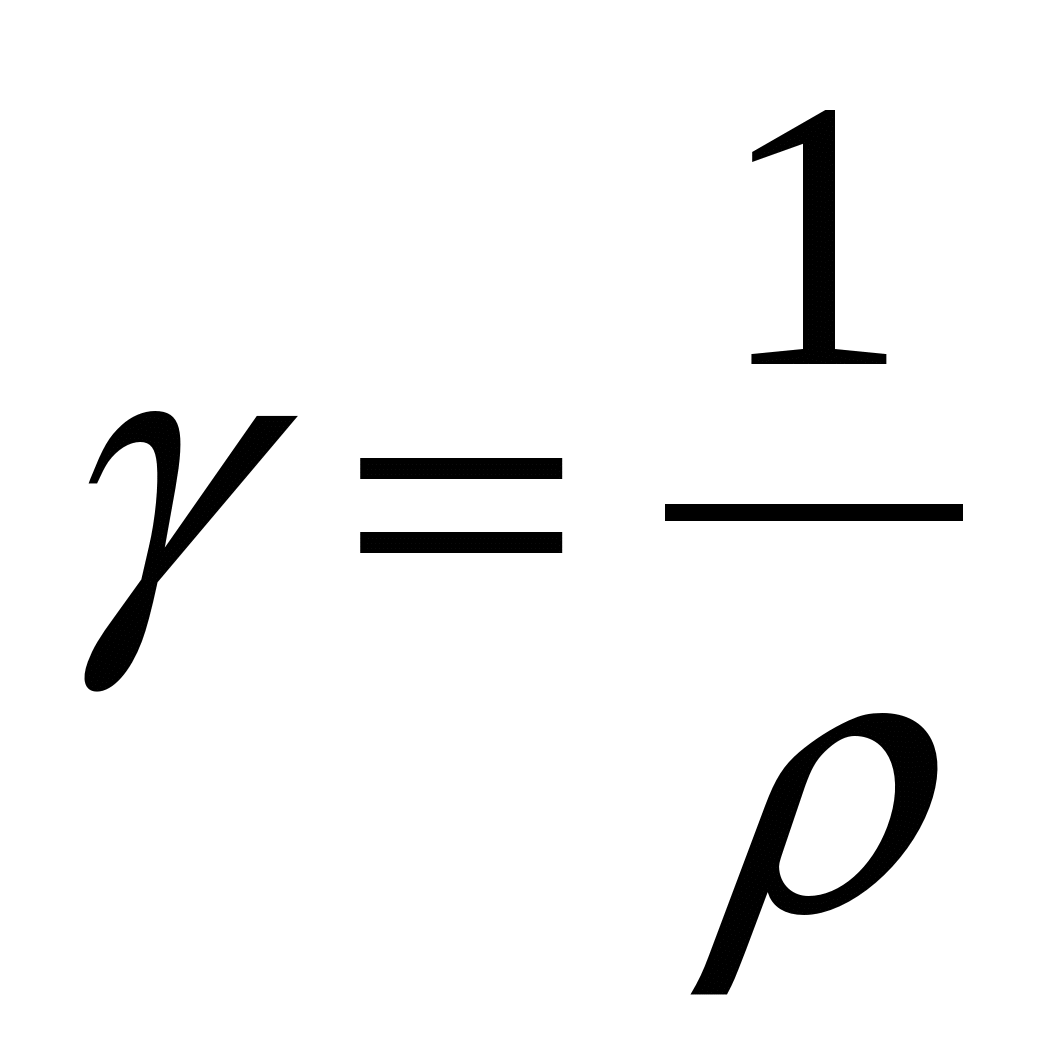 .
.Тогда закону Ома в дифференциальной форме (15.4) можно придать вид 
^
15.4. Закон Джоуля-Ленца
15.4.1. Закон Джоуля-Ленца в интегральной форме
Джоуль и независимо от него Ленц экспериментально установили, сто количество теплоты, выделенной в проводнике сопротивлением R за время dt , пропорционально квадрату силы тока, сопротивлению и времени: 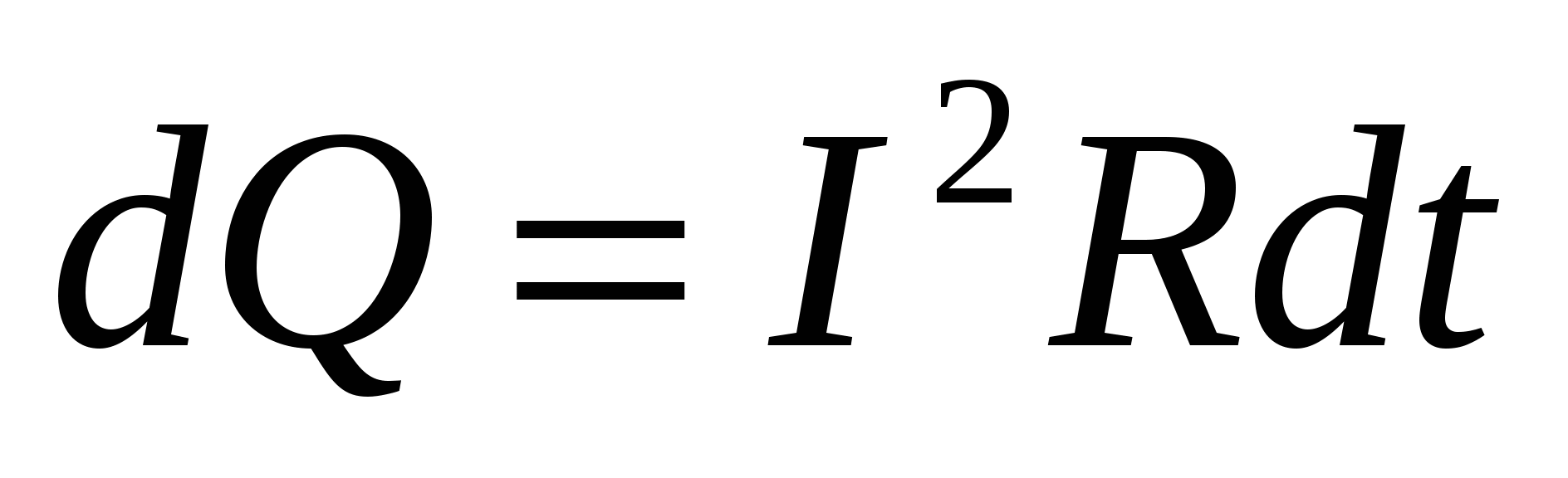 . . | (15.16) |
Формула (15.16) представляет закон Джоуля-Ленца в интегральной форме.
^
15.4.2. Закон Джоуля-Ленца в дифференциальной форме
Выделим, как и ранее, внутри проводника элементарный цилиндрический объем (рис. 15.3). Заменим в (15.16)
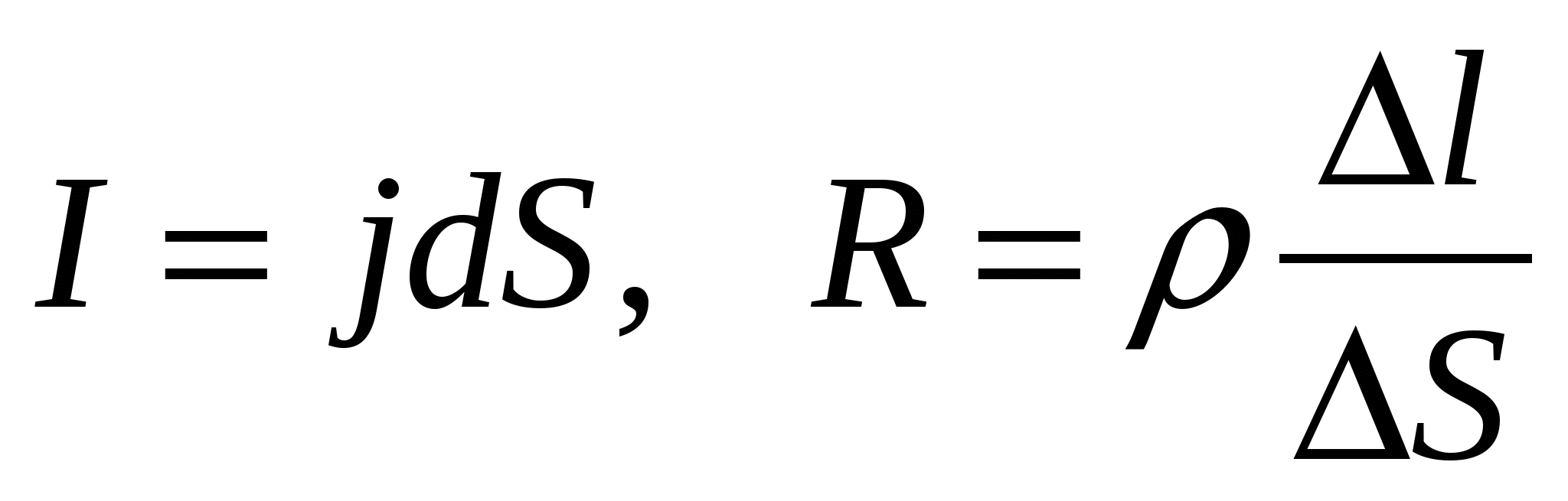 . Тогда
. Тогда где V=
l
S
– объем проводника. Введем в рассмотрение удельную мощность теплоты
где V=
l
S
– объем проводника. Введем в рассмотрение удельную мощность теплоты 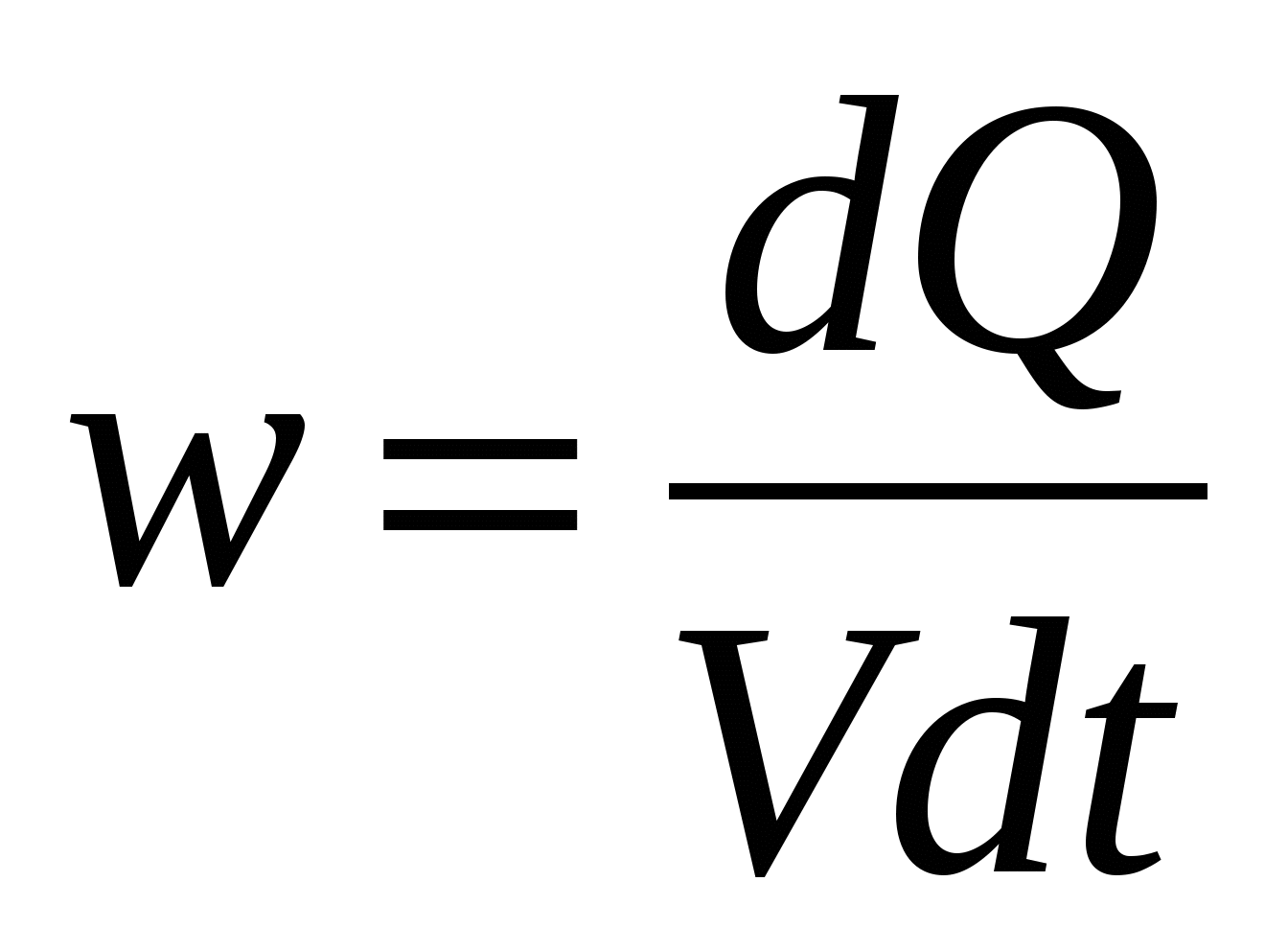 [Дж/м 3 с = Вт/м 3 ]. [Дж/м 3 с = Вт/м 3 ]. | (15.18) |
Удельная мощность теплоты численно равна количеству теплоты, выделенной в единице объема проводника за единицу времени. Другими словами – это тепловая мощность, развиваемая в единице объема. С учетом (15.18) выражению (15.17) можно придать вид
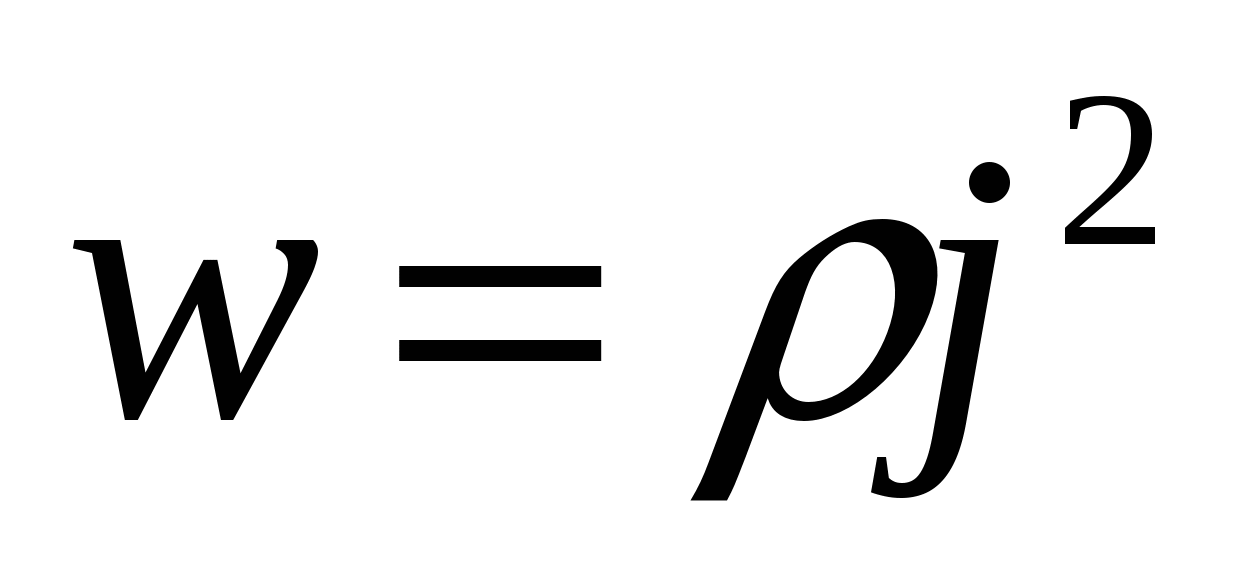 .
.
Формулы (15.19) и (15.20) представляют закон Джоуля-Ленца в дифференциальной форме.
Лекція 24.
^
15.5. Обоснование законов Ома и Джоуля-Ленца по классической электронной теории
В классической электронной теории металлов принимается следующая модель.
1. Носителями тока в металлах являются свободные электроны.
2. Свободные электроны образуют электронный газ, который по своим свойствам аналогичен идеальному газу. Имеется лишь одно различие: электроны при своем движении сталкиваются не между собой, а с ионами кристаллической решетки.
3. Под действием электрического поля электроны наряду с хаотическим движением со скоростью  начинают двигаться направлено со скоростью
начинают двигаться направлено со скоростью  . При этом скорость направленного движения значительно меньше скорости хаотического движения
. При этом скорость направленного движения значительно меньше скорости хаотического движения
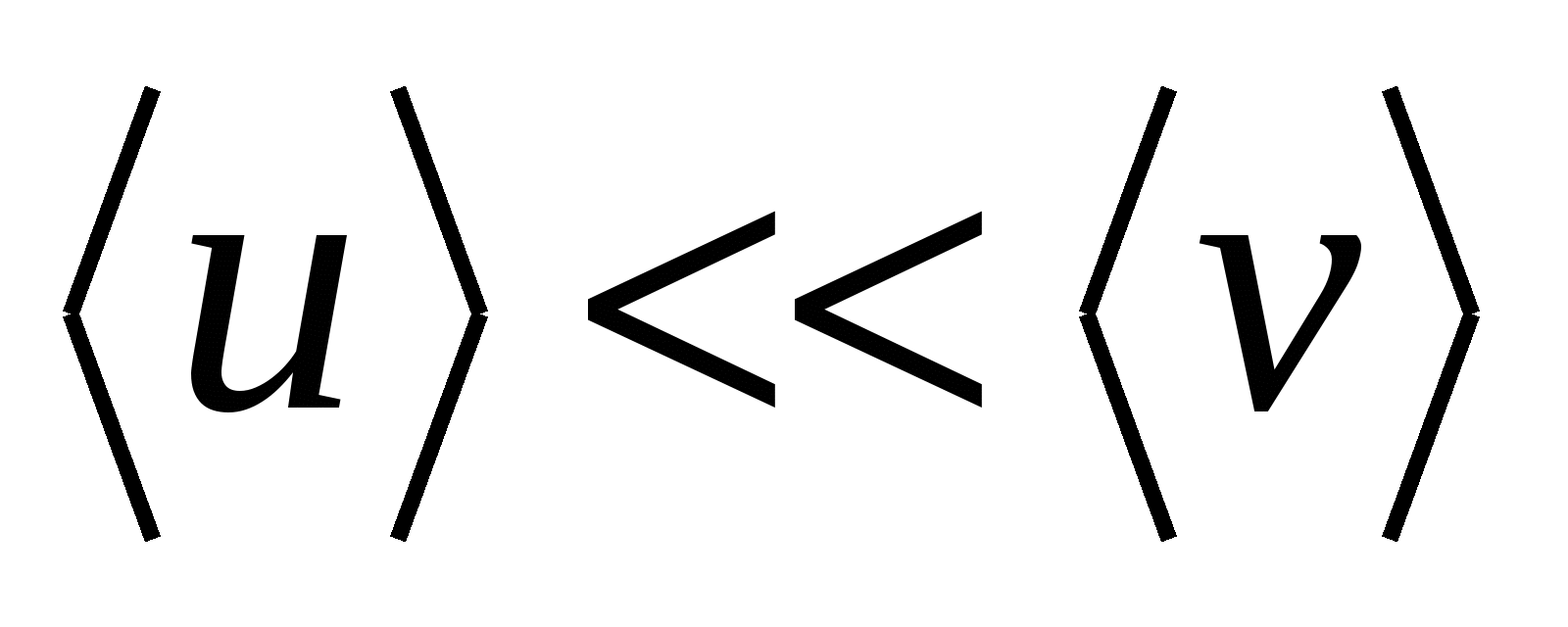 . . | (15.21) |
Найдем скорость направленного движения электронов. Предположим, что в момент времени t= 0 скорость направленного движения электронов u 0 =0. Под действием силы F=eE электрон в соответствии со вторым законом Ньютона начинает двигаться ускоренно:
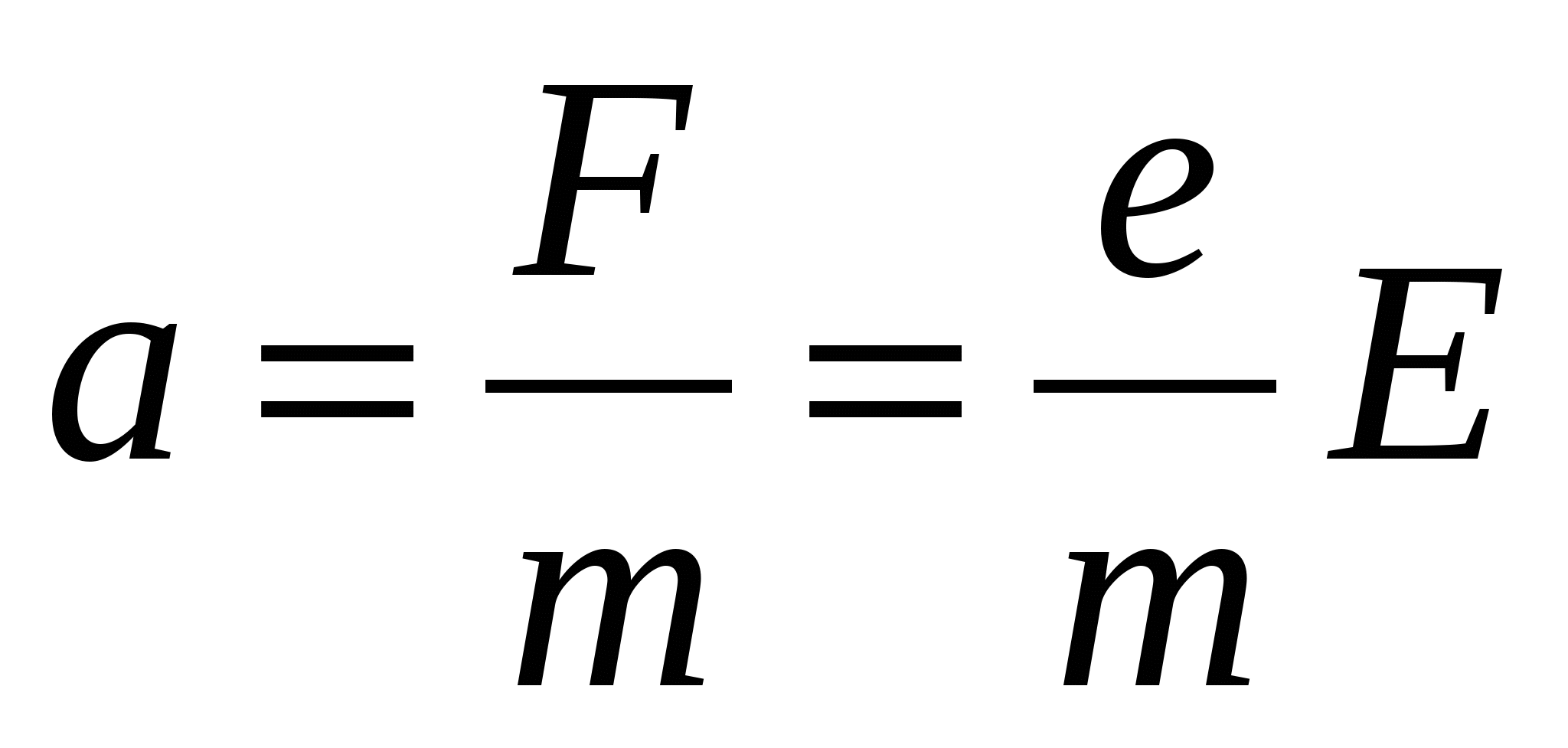 .
.
Скорость направленного движения электрона
 . . | (15.22) |

Рис. 15.4
Из формулы (15.22) следует, что скорость электрона u
с течением времени должна возрастать неограниченно. Однако через некоторый промежуток времени электрон испытывает столкновение с ионом кристаллической решетки и останавливается. Схематически зависимость скорости направленного движения от времени изображена на рис. 15.4.
Среднее время между двумя последовательными столкновениями электрона
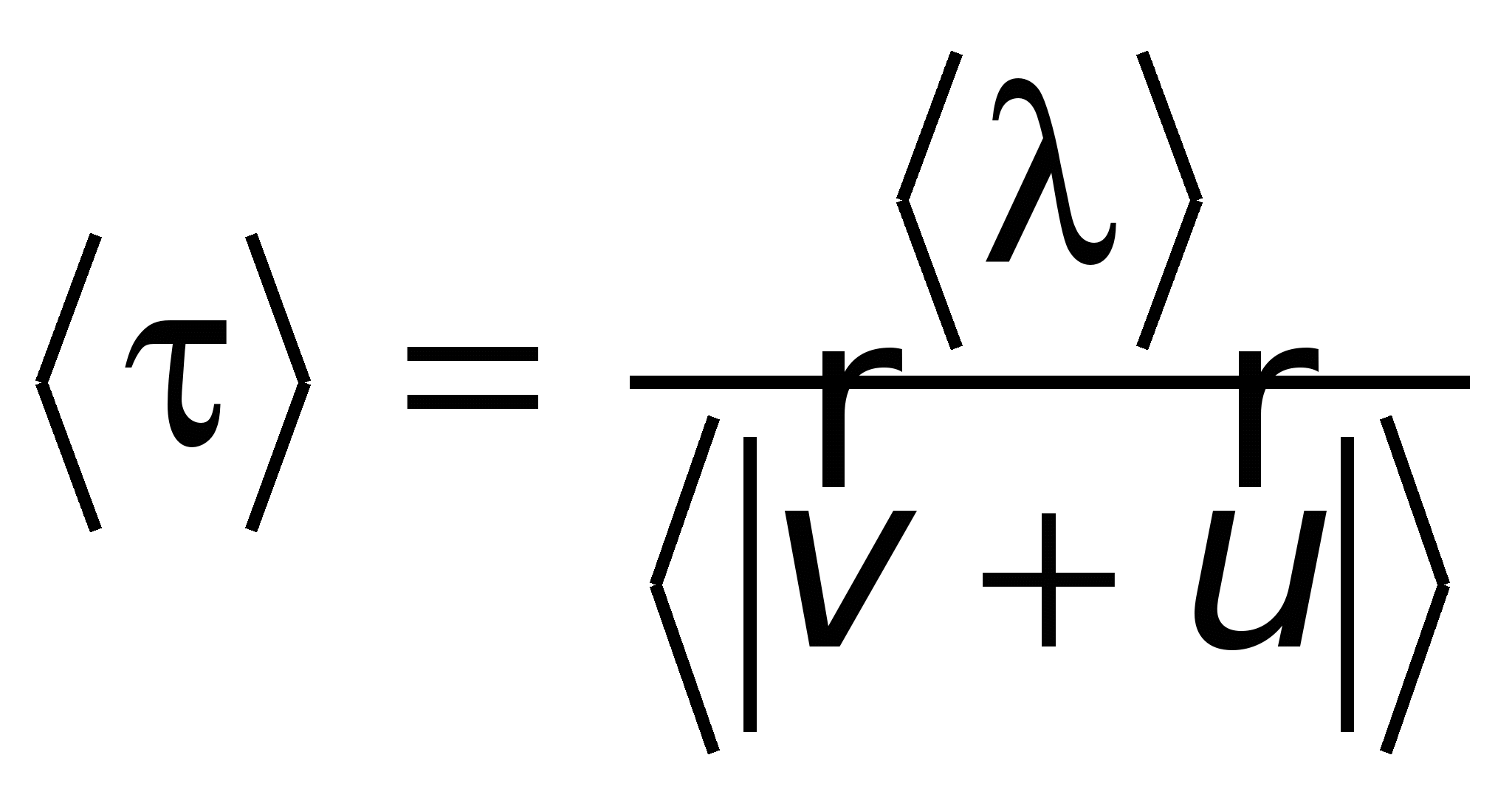 , , | (15.23) |
где
 – средняя длина свободного пробега электрона;
– средняя длина свободного пробега электрона;  – среднее значение его скорости, которая является векторной суммой скоростей хаотического и направленного движений.
– среднее значение его скорости, которая является векторной суммой скоростей хаотического и направленного движений.В силу неравенства (15.21) скоростью направленного движения можно пренебречь, поэтому
 . .
через характеристики электронного газа. Исходя из представлений классической электронной теории металлов, получим теперь закон Джоуля–Ленца. К концу свободного пробега электрон обладает кинетической энергией направленного движения
Подставляя сюда значение максимальной скорости направленного движения электрона из (15.25) и учитывая, что среднее число столкновений за 1 с
получаем закон Джоуля–Ленца
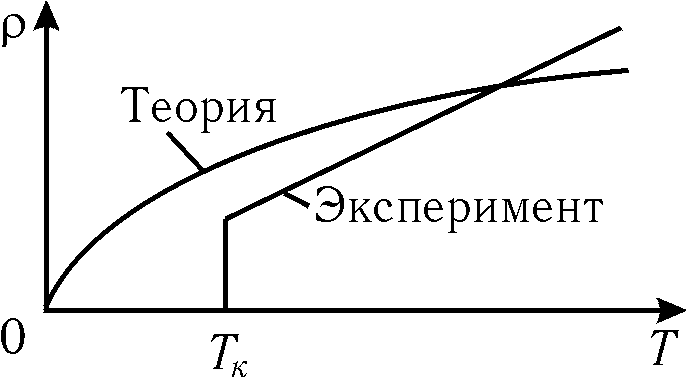
Из сопоставления (15.30) и (15.20) находим такое же выражение для удельной теплопроводности, как и в законе Ома (см. (15.28)). Несмотря на очевидные успехи классической электронной теории металлов, она, тем не менее, столкнулась с рядом трудностей. В частности классическая теория неправильно предсказывает зависимость сопротивления металла от температуры. Анализ выражения (15.29) показывает, что от температуры зависит лишь скорость хаотического движения. При этом (см. формулу (8.18)) Рис. 15.5
Первое правило Кирхгофа.
Алгебраическая сумма токов, сходящихся в узле, равна нулю, т.е.
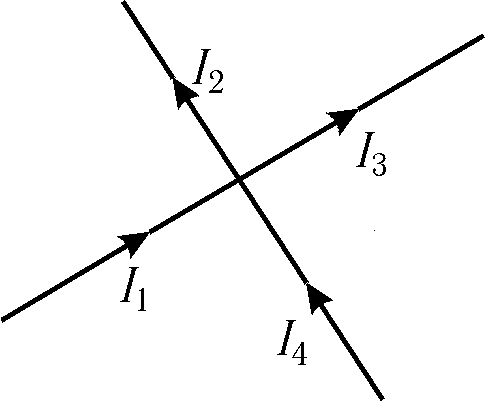
Узлом называется точка цепи, где пересекаются три и более проводников. Ток берется со знаком "+", если он входит в узел; выходящий из узла ток берется со знаком "-". Рис. 15.6
т.е. сумма токов, входящих в узел, равна сумме токов, выходящих из него. Первое правило Кирхгофа – следствие закона сохранения электрического заряда: заряды, попав в узел, никуда не исчезают и не накапливаются. ^
Второе правило Кирхгофа.
Алгебраическая сумма падений напряжения в замкнутом контуре, выделенном из сложной цепи, равна алгебраической сумме ЭДС, включенных в этот контур:
Падение напряжения берется со знаком "+", если ток направлен в сторону обхода контура, и "-" в противном случае. ЭДС берется со знаком "+", если она действует в направлении обхода, и "-" – в противном случае. Направление обхода выбирается произвольно. Для определенности выберем направление обхода по часовой стрелке. Запишем для примера второе правило Кирхгофа для контуров ^ ABCFA и ABCDEFA (рис. 15.7): контур ABCFA : I 1 R 1 + I 2 R 2 = E 1 – E 2 ; контур ABCDEFA: I 1 R 1 - I 3 R 3 = E 1 – E 3 . В общем случае, когда в цепи имеется n узлов и m контуров, нужно составить n -1 уравнение по первому правилу Кирхгофа и m -1 уравнение по второму правилу. 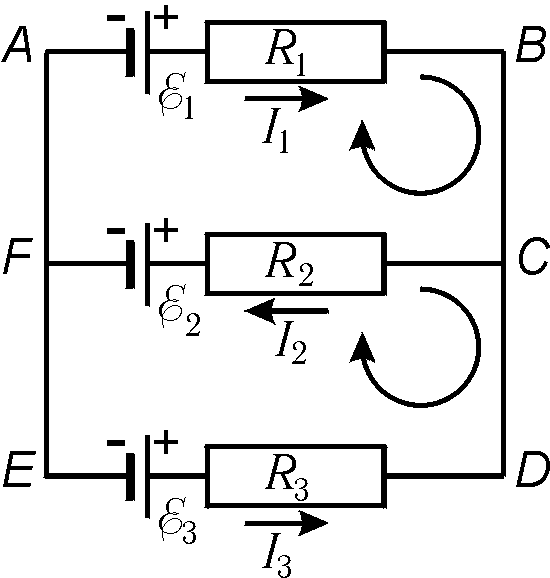 Рис. 15.7
Лекція 25. |
1. Энергия системы неподвижных точечных зарядов. Электростатические силы взаимодействия консервативны; следовательно, система зарядов обладает потенциальной энергией. Найдем потенциальную энергию системы двух неподвижных точечных зарядов и , находящихся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией:
, ![]() ,
,
где и - соответственно потенциалы, создаваемые зарядом в точке нахождения заряда и зарядом в точке нахождения заряда . Согласно формуле (8.3.6),
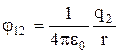 и
и 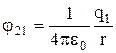 ,
,
![]()
Добавляя к системе из двух зарядов последовательно заряды , , …, можно убедиться в том, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна
 , (8.12.1.)
, (8.12.1.)
где - потенциал, создаваемый в той точке, где находится заряд , всеми зарядами, кроме i-го.
2. Энергия заряженного уединенного проводника. Пусть имеется уединенный проводник, заряд, емкость и потенциал которого соответственно равны q, C, . Увеличим заряд этого проводника на dq. Для этого необходимо перенести заряд dq из бесконечности на уединенный проводник, затратив на это работу, равную
![]() .
.
Чтобы зарядить тело от нулевого потенциала до , необходимо совершить работу
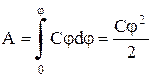 . (8.12.2.)
. (8.12.2.)
Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:
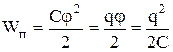 . (8.12.3.)
. (8.12.3.)
Формулу (8.12.3.) можно получить и из того, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Полагая потенциал проводника равным , из (8.12.1.) найдем
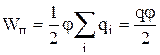 ,
,
где - заряд проводника.
3. Энергия заряженного конденсатора. Как всякий заряженный проводник, конденсатор обладает энергией, которая в соответствии с формулой (8.12.3.) равна
 , (8.12.4.)
, (8.12.4.)
где q - заряд конденсатора, C - его емкость, - разность потенциалов между обкладками.
4. Энергия электростатического поля. Преобразуем формулу (8.12.4.), выражающую энергию плоского конденсатора посредством зарядов и потенциалов, воспользовавшись выражением для емкости плоского конденсатора и разности потенциалов между его обкладками (). Тогда получим
 , (8.12.5.)
, (8.12.5.)
где V=Sd - объем конденсатора. Формула (8.12.5.) показывает, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, - напряженность Е .
Формулы (8.12.4.) и (8.12.5.) соответственно связывают энергию конденсатора с зарядом на его обкладках и с напряженностью поля. Возникает, естественно, вопрос о локализации электростатической энергии и что является ее носителем - заряды или поле? Ответ на этот вопрос может дать только опыт. Электростатика изучает постоянные во времени поля неподвижных зарядов, т.е. в ней поля и обусловившие их заряды неотделимы друг от друга. Поэтому электростатика ответить на поставленные вопросы не может. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать обособленно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, способных переносить энергию. Это убедительно подтверждает основное положение теории близкодействия о локализации энергии в поле и что носителем энергии является поле.
Объемная плотность энергии электростатического поля (энергия единицы объема)
 . (8.12.6.)
. (8.12.6.)
Выражение (8.12.6.) справедливо только для изотропного диэлектрика, для которого выполняется соотношение: .
Электрическую энергию плоского конденсатора можно выразить через напряженность поля между его обкладками:
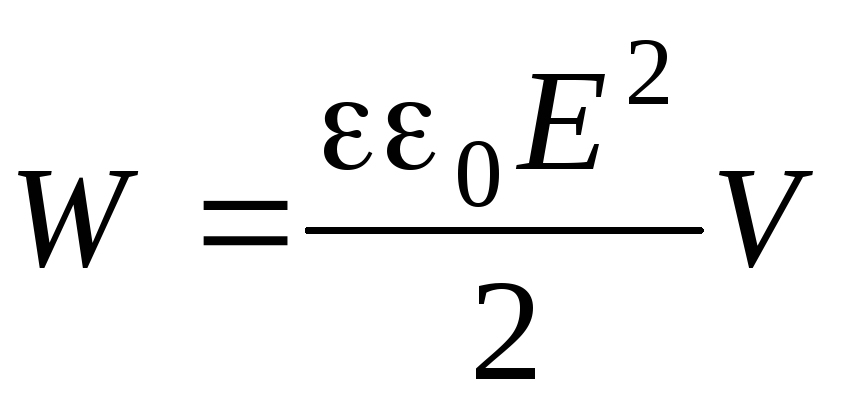 ,
,
где - объем пространства, занятого полем, S – площадь обкладок, d – расстояние между ними. Оказывается, через напряженность можно выразить электрическую энергию и произвольной системы заряженных проводников и диэлектриков:
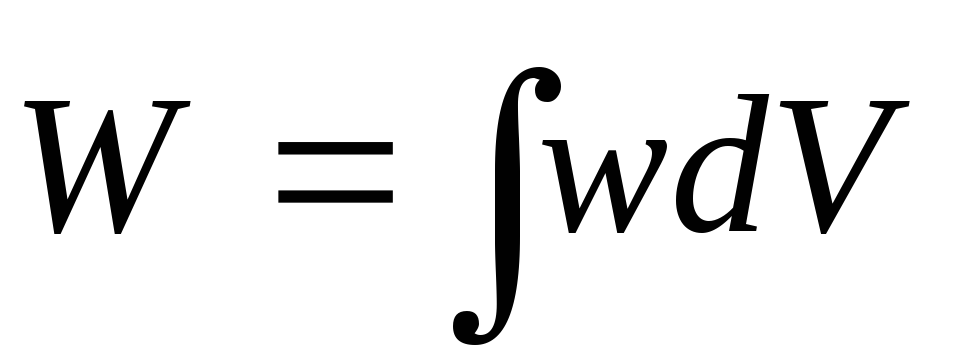 ,
(5)
,
(5)
 ,
,
а интегрирование
проводится по всему пространству,
занятому полем (предполагается, что
диэлектрик изотропный и
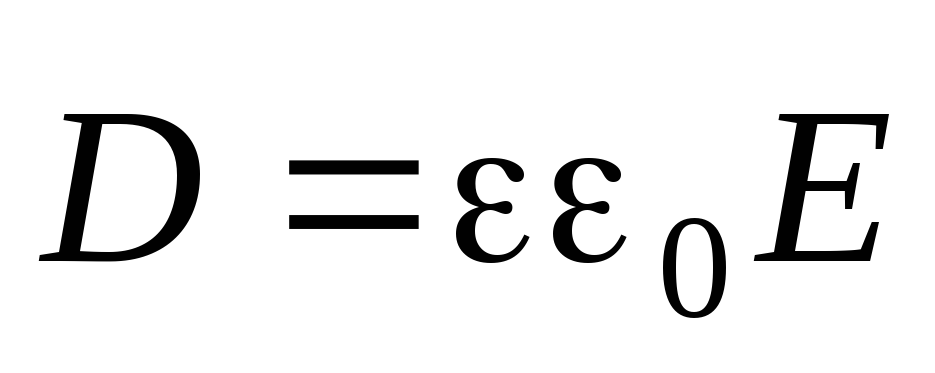 ).
Величинаw
представляет собой электрическую
энергию, приходящуюся на единицу объема.
Вид формулы (5) дает основания предположить,
что электрическая энергия заключена
не во взаимодействующих зарядах, а в их
электрическом поле, заполняющем
пространство. В рамках электростатики
это предположение проверить экспериментально
или обосновать теоретически невозможно,
однако рассмотрение переменных
электрических и магнитных полей позволяет
удостоверится в правильности такой
полевой интерпретации формулы (5).
).
Величинаw
представляет собой электрическую
энергию, приходящуюся на единицу объема.
Вид формулы (5) дает основания предположить,
что электрическая энергия заключена
не во взаимодействующих зарядах, а в их
электрическом поле, заполняющем
пространство. В рамках электростатики
это предположение проверить экспериментально
или обосновать теоретически невозможно,
однако рассмотрение переменных
электрических и магнитных полей позволяет
удостоверится в правильности такой
полевой интерпретации формулы (5).
7. Энергия электрического поля (Примеры решения задач) Энергия взаимодействия зарядов
Пример 1.
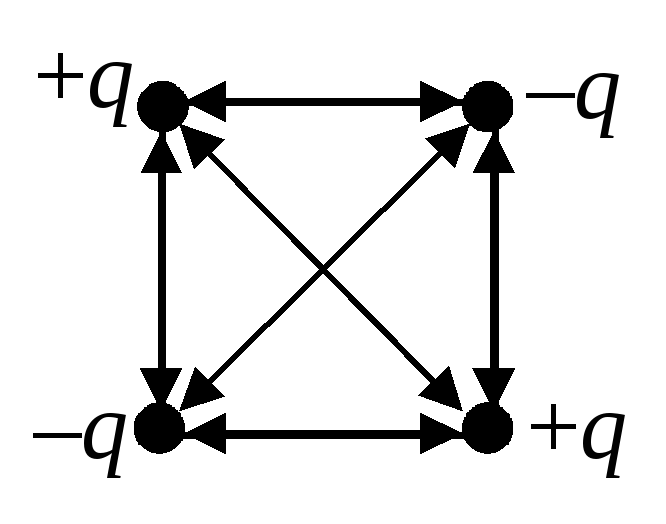
Определите электрическую энергию взаимодействия точечных зарядов, расположенных в вершинах квадрата со стороной a (см. рис.2).
Решение .
На рис.3 условно изображены двунаправленными стрелками все парные взаимодействия зарядов. Учитывая энергии всех этих взаимодействий, получим:
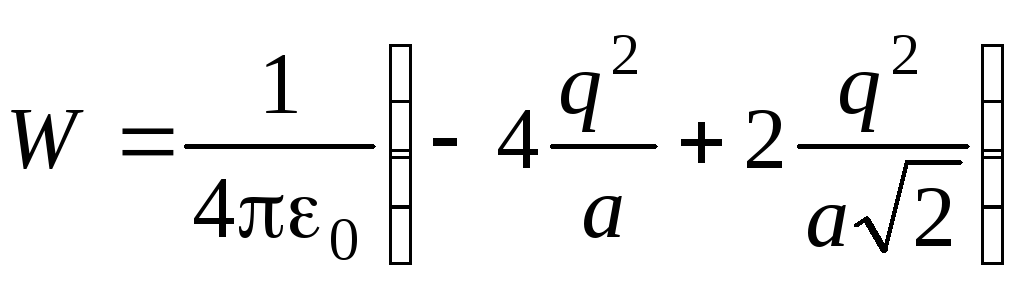 .
.
|
|
|
|
Пример 2.
Определите электрическую энергию взаимодействия заряженного кольца с диполем, расположенным на его оси, как показано на рис.4. Известны расстояния a , l , заряды Q , q и радиус кольца R .
Решение .
При решении задачи следует учесть все энергии парных взаимодействий зарядов одного тела (кольца) с зарядами другого тела (диполя). Энергия взаимодействия точечного заряда q с зарядомQ , распределенным по кольцу, определяется суммой
![]() ,
,
где
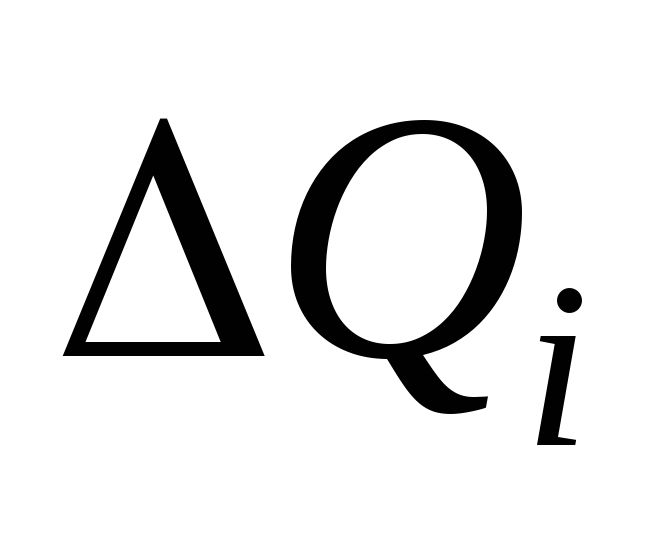 - заряд
бесконечно малого фрагмента кольца,
- заряд
бесконечно малого фрагмента кольца,
 -
расстояние
от этого фрагмента до зарядаq
.
Поскольку все
-
расстояние
от этого фрагмента до зарядаq
.
Поскольку все одинаковы и равны
одинаковы и равны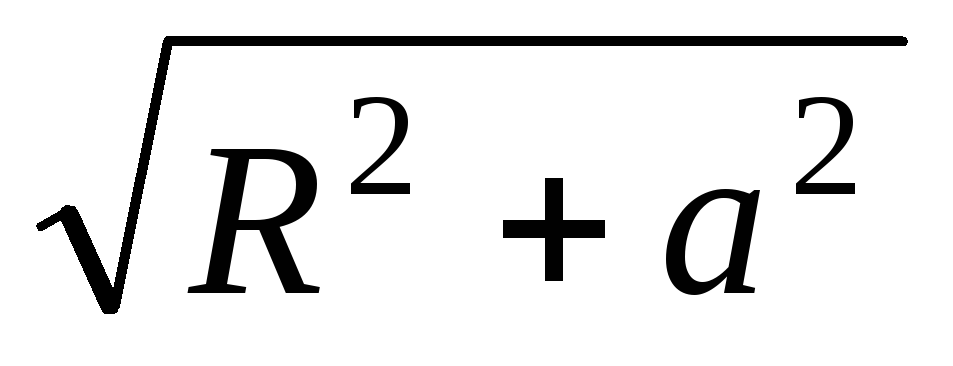 ,
то
,
то
Аналогично найдем энергию взаимодействия точечного заряда –q с заряженным кольцом:
Суммируя W 1 иW 2 , получим для энергии взаимодействия кольца с диполем:
 .
.
Электрическая энергия заряженных проводников
Пример 3.
Определите работу электрических сил при уменьшении в 2 раза радиуса однородно заряженной сферы. Заряд сферы q , ее первоначальный радиус R .
Решение .
Электрическая энергия уединенного
проводника определяется формулой
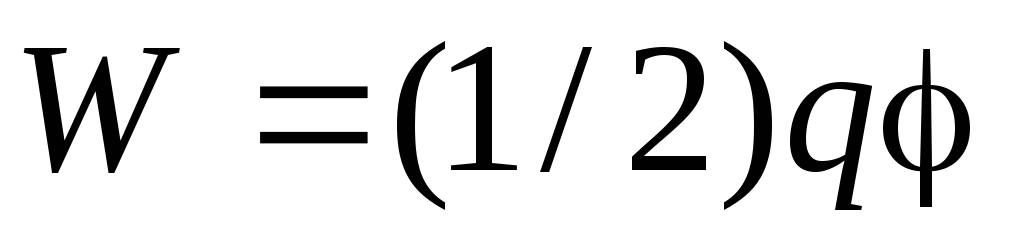 ,
гдеq
–
заряд проводника,- его
потенциал. Учитывая, что потенциал
однородно заряженной сферы радиусаR
равен
,
гдеq
–
заряд проводника,- его
потенциал. Учитывая, что потенциал
однородно заряженной сферы радиусаR
равен ,
найдем ее электрическую энергию:
,
найдем ее электрическую энергию:
 .
.
После уменьшения в два раза радиуса сферы ее энергия становится равной
 .
.
Электрические силы при этом совершают работу
 .
.
Пример 4.
Два металлических шара, радиусы которых r и 2r , а соответствующие заряды 2q и –q , расположены в вакууме на большом расстоянии друг от друга. Во сколько раз уменьшится электрическая энергия системы, если шары соединить тонкой проволокой?
Решение .
После соединения шаров тонкой проволокой их потенциалы становятся одинаковыми
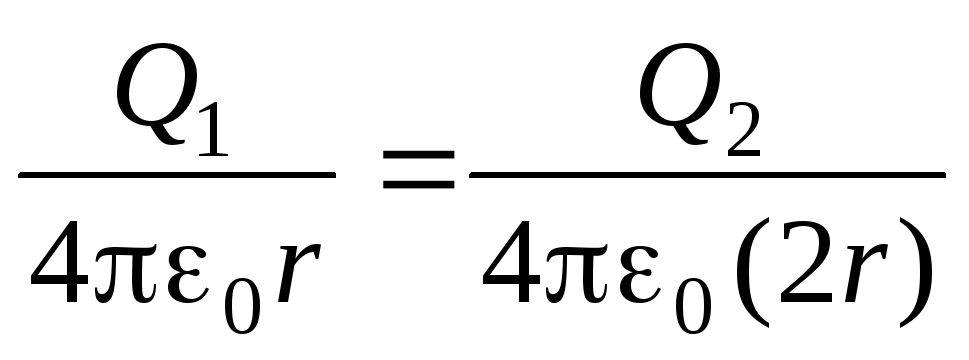 ,
,
а установившиеся заряды шаров Q 1 и Q 2 получаются в результате перетекания заряда с одного шара на другой. При этом суммарный заряд шаров остается постоянным:
 .
.
Из этих уравнений найдем
 ,
, .
.
Энергия шаров до соединения их проволокой равна
 ,
,
а после соединения
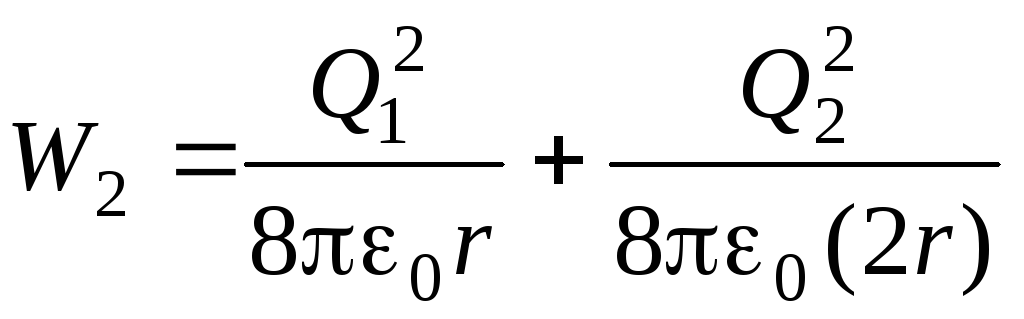 .
.
Подставляя в последнее выражение значения Q 1 и Q 2 , получим после простых преобразований
 .
.
Пример 5.
В один шар слились N = 8 одинаковых шариков ртути, заряд каждого из которых q . Считая, что в начальном состоянии ртутные шарики находились на большом расстоянии друг от друга, определите, во сколько раз увеличилась электрическая энергия системы.
Решение .
При слиянии ртутных шариков сохраняется их суммарный заряд и объем:
![]() ,
,
где Q – заряд шара, R – его радиус, r – радиус каждого маленького ртутного шарика. Суммарная электрическая энергия N уединенных шариков равна
 .
.
Электрическая энергия полученного в результате слияния шара
 .
.
После алгебраических преобразований получим
 = 4.
= 4.
Пример 6.
Металлический шарик радиуса R = 1 мм и заряда q = 0,1 нКл с большого расстояния медленно приближают к незаряженному проводнику и останавливают, когда потенциал шарика становится равным = 450 В. Какую работу для этого следует совершить?
Решение .
Электрическая энергия системы из двух заряженных проводников определяется формулой
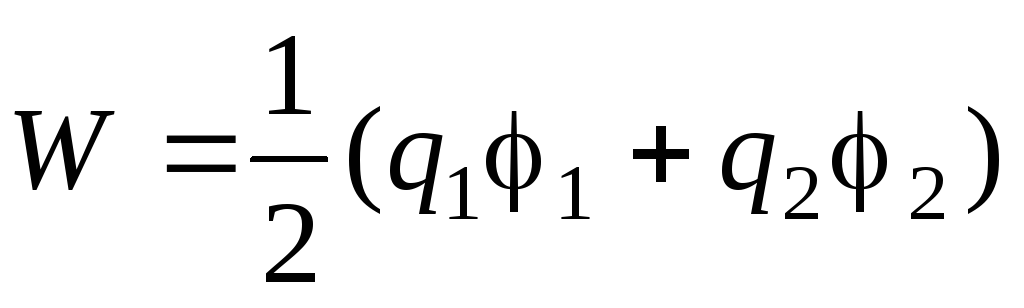 ,
,
где q 1 иq 2 – заряды проводников, 1 и 2 – их потенциалы. Так как проводник по условию задачи не заряжен, то
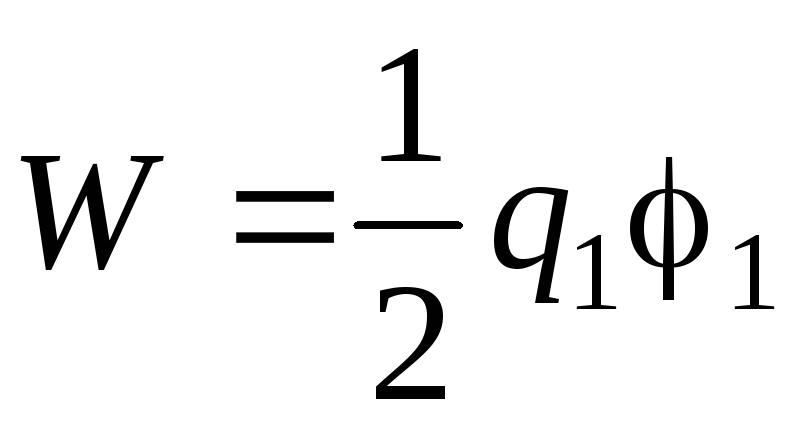 ,
,
где q 1 и 1 заряд и потенциал шара. Когда шар и незаряженный проводник находятся на большом расстоянии друг от друга,
 ,
,
и электрическая энергия системы
 .
.
В конечном состоянии системы, когда потенциал шара стал равным , электрическая энергия системы:
 .
.
Работа внешних сил равна приращению электрической энергии:
 = –0,0225 мкДж.
= –0,0225 мкДж.
Заметим, что электрическое поле в конечном состоянии системы создается зарядами, индуцированными на проводнике, а также зарядами, неоднородно распределенными по поверхности металлического шара. Рассчитать это поле при известной геометрии проводника и заданном положении металлического шара весьма непросто. Нам не потребовалось этого делать, поскольку в задаче задана не геометрическая конфигурация системы, а потенциал шара в конечном состоянии.
Пример 7 .
Система состоит
из двух концентрических тонких
металлических оболочек с радиусами R
1
и R
2
( и
соответствующими зарядамиq
1
и q
2 .
Найдите электрическую энергию W
системы. Рассмотрите также специальный
случай, когда
и
соответствующими зарядамиq
1
и q
2 .
Найдите электрическую энергию W
системы. Рассмотрите также специальный
случай, когда
![]() .
.
Решение .
Электрическая энергия системы из двух заряженных проводников определяется формулой
 .
.
Для решения задачи необходимо найти потенциалы внутренней ( 1) и внешней ( 2) сфер. Это нетрудно сделать (см. соответствующий раздел пособия):
 ,
, .
.
Подставляя эти выражения в формулу для энергии, получим
 .
.
При
![]() энергия равна
энергия равна
 .
.
Вопрос №1
Электрическое поле. Для объяснения природы электрических взаимодействий заряженных тел необходимо допустить наличие в окружающем заряды пространстве физического агента, осуществляющего это взаимодействие. В соответствии с теорией близкодействия , утверждающей, что силовые взаимодействия между телами осуществляются через посредство особой материальной среды, окружающей взаимодействующие тела и передающей любые изменения таких взаимодействий в пространстве с конечной скоростью, таким агентом является электрическое поле .
Электрическое поле создается как неподвижными, так и движущимися зарядами. О наличии электрического поля можно судить, прежде всего, по его способности оказывать силовое действие на электрические заряды, движущиеся и неподвижные, а также по способности индуцировать электрические заряды на поверхности проводящих нейтральных тел.
Поле, создаваемое неподвижными электрическими зарядами, называют стационарным электрическим , или электростатическим полем. Оно представляет собой частный случай электромагнитного поля , посредством которого осуществляются силовые взаимодействия между электрически заряженными телами, движущимся в общем случае произвольным образом относительно системы отсчета.
Напряженность электрического поля. Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E , называемая напряжённостью электрического поля .
E = F / q пр.
Она определяется отношением силы F , действующей со стороны поля на точечный пробный заряд q пр, помещенный в рассматриваемую точку поля, к величине этого заряда.
Понятие «пробный заряд» предполагает, что этот заряд не участвует в создании электрического поля и так мал, что не искажает его, т. е. не вызывает перераспределения в пространстве зарядов, создающих рассматриваемое поле. В системе СИ единицей напряженности служит 1 В / м, что эквивалентно 1 Н / Кл.
Напряженность поля точечного заряда. Используя закон Кулона найдем выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда:
В этой формуле r – радиус-вектор, соединяющий заряды q и q пр. Из (1.2) следует, что напряжённость E поля точечного заряда q во всех точках поля направлена радиально от заряда при q > 0 и к заряду при q < 0.
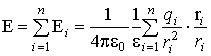 Принцип суперпозиции.
Напряжённость поля, создаваемого системой неподвижных точечных зарядов q
1 , q
2 , q
3 , ¼, q n
, равна векторной сумме напряжённостей электрических полей, создаваемых каждым из этих зарядов в отдельности:
Принцип суперпозиции.
Напряжённость поля, создаваемого системой неподвижных точечных зарядов q
1 , q
2 , q
3 , ¼, q n
, равна векторной сумме напряжённостей электрических полей, создаваемых каждым из этих зарядов в отдельности:
, где r i
– расстояние между зарядом q i
и рассматриваемой точкой поля.
Принцип суперпозиции , позволяет рассчитывать не только напряжённость поля системы точечных зарядов, но и напряженность поля в системах, где имеет место непрерывное распределение заряда. Заряд тела можно представить как сумму элементарных точечных зарядов dq .
При этом, если заряд распределен с линейной плотностью t, то dq = tdl ; если заряд распределен с поверхностной плотностью s, то dq = dl и dq = rdl , если заряд распределен с объёмной плотностью r.
Вопрос №2
Поток вектора электрической индукции. Поток вектора электрической индукцииопределяется аналогично потоку вектора напряженности электрического поля
dF D = D dS
В определениях потоков заметна некоторая неоднозначность, связанная с тем, что для каждой поверхности можно задать две нормали противоположного направления. Для замкнутой поверхности положительной считается внешняя нормаль.
Теорема Гаусса.
Рассмотрим точечный положительный электрический заряд q, находящийся внутри произвольной замкнутой поверхности S (рис. 1.3). Поток вектора индукции через элемент поверхности dS равен![]()
Составляющую dS D = dS cosa элемента поверхности dS в направлении вектора индукции D рассматриваем как элемент сферической поверхности радиуса r, в центре которой расположен заряд q.
Учитывая, что dS D / r 2 равен элементарному телесному углу dw, под которым из точки нахождения заряда q виден элемент поверхности dS, преобразуем выражение (1.4) к виду dF D = q dw / 4p, откуда после интегрирования по всему окружающему заряд пространству, т. е. в пределах телесного угла от 0 до 4p, получим
Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен заряду, заключенному внутри этой поверхности.
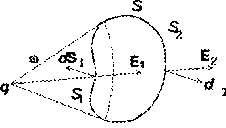
Если произвольная замкнутая поверхность S не охватывает точечный заряд q, то, построив коническую поверхность с вершиной в точке нахождения заряда, разделим поверхность S на две части: S 1 и S 2 . Поток вектора D через поверхность S найдем как алгебраическую сумму потоков через поверхности S 1 и S 2:
![]() .
.
Обе поверхности из точки нахождения заряда q видны под одним телесным углом w. Поэтому потоки равны
Поскольку при вычислении потока через замкнутую поверхность используется внешняя нормаль к поверхности, легко видеть, что поток Ф 1D < 0, тогда как поток Ф 2D > 0. Суммарный поток Ф D = 0. Это означает, что поток вектора электрической индукции через замкнутую поверхность произвольной формы не зависит от зарядов, расположенных вне этой поверхности.
Если электрическое поле создаётся системой точечных зарядов q 1 , q 2 ,¼, q n , которая охватывается замкнутой поверхностью S, то, в соответствии с принципом суперпозиции, поток вектора индукции через эту поверхность определяется как сумма потоков, создаваемых каждым из зарядов. Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен алгебраической сумме зарядов, охваченных этой поверхностью:
Следует отметить, что заряды q i не обязательно должны быть точечными, необходимое условие - заряженная область должна полностью охватываться поверхностью. Если в пространстве, ограниченном замкнутой поверхностью S, электрический заряд распределен непрерывно, то следует считать, что каждый элементарный объём dV имеет заряд . В этом случае в правой части выражения алгебраическое суммирование зарядов заменяется интегрированием по объёму, заключённому внутри замкнутой поверхности S:
Это выражение является наиболее общей формулировкой теоремы Гаусса: поток вектора электрической индукции через замкнутую поверхность произвольной формы равен суммарному заряду в объеме, охваченном этой поверхностью, и не зависит от зарядов, расположенных вне рассматриваемой поверхности ![]() .
.
Вопрос №3
Потенциальная энергия заряда в электрическом поле.
Работу, совершаемую силами электрического поля при перемещении положительного точечного заряда q
из положения 1 в положение 2, представим как изменение потенциальной энергии этого заряда: ![]() , где W
п1 и W
п2 – потенциальные энергии заряда q
в положениях 1 и 2. При малом перемещении заряда q
в поле, создаваемом положительным точечным зарядом Q
, изменение потенциальной энергии равно
, где W
п1 и W
п2 – потенциальные энергии заряда q
в положениях 1 и 2. При малом перемещении заряда q
в поле, создаваемом положительным точечным зарядом Q
, изменение потенциальной энергии равно ![]() . При конечном перемещении заряда q
из положения 1 в положение 2, находящиеся на расстояниях r
1 и r
2 от заряда Q
, . Если поле создано системой точечных зарядов Q
1 , Q
2 ,¼, Q
n , то изменение потенциальной энергии заряда q
в этом поле:
. При конечном перемещении заряда q
из положения 1 в положение 2, находящиеся на расстояниях r
1 и r
2 от заряда Q
, . Если поле создано системой точечных зарядов Q
1 , Q
2 ,¼, Q
n , то изменение потенциальной энергии заряда q
в этом поле:  . Приведённые формулы позволяют найти только изменение
потенциальной энергии точечного заряда q
, а не саму потенциальную энергию. Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q
, находящегося в электрическом поле, созданном другим точечным зарядом Q
, получим
. Приведённые формулы позволяют найти только изменение
потенциальной энергии точечного заряда q
, а не саму потенциальную энергию. Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q
, находящегося в электрическом поле, созданном другим точечным зарядом Q
, получим
![]() , где C
– произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q
(при r
® ¥), тогда постоянная C
= 0 и предыдущее выражение принимает вид . При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную
.В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q
:
, где C
– произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q
(при r
® ¥), тогда постоянная C
= 0 и предыдущее выражение принимает вид . При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную
.В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q
:
![]() .
.
![]() Потенциальная энергия системы точечных зарядов.
В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Q i
(i
= 1, 2, ... , n
). Энергиявзаимодействия всех n
зарядов определится соотношением, где r ij -
расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.
Потенциальная энергия системы точечных зарядов.
В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Q i
(i
= 1, 2, ... , n
). Энергиявзаимодействия всех n
зарядов определится соотношением, где r ij -
расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.
Потенциал электростатического поля. Поле консервативной силы может быть описано не только векторной функцией, но эквивалентное описание этого поля можно получить, определив в каждой его точке подходящую скалярную величину. Для электростатического поля такой величиной является потенциал электростатического поля , определяемый как отношение потенциальной энергии пробного заряда q к величине этого заряда, j = W п / q , откуда следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Единицей измерения потенциала служит Вольт (1 В).
Потенциал поля точечного заряда Q в однородной изотропной среде с диэлектрической проницаемостью e: .
![]()
![]() Принцип суперпозиции.
Потенциал есть скалярная функция, для неё справедлив принцип суперпозиции. Так для потенциала поля системы точечных зарядов Q
1, Q
2 ¼, Q n
имеем, где r i
- расстояние от точки поля, обладающей потенциалом j, до заряда Q i
. Если заряд произвольным образом распределен в пространстве, то, где r
- расстояние от элементарного объема dx
, dy
, dz
до точки (x
, y
, z
), где определяется потенциал; V
- объем пространства, в котором распределен заряд.
Принцип суперпозиции.
Потенциал есть скалярная функция, для неё справедлив принцип суперпозиции. Так для потенциала поля системы точечных зарядов Q
1, Q
2 ¼, Q n
имеем, где r i
- расстояние от точки поля, обладающей потенциалом j, до заряда Q i
. Если заряд произвольным образом распределен в пространстве, то, где r
- расстояние от элементарного объема dx
, dy
, dz
до точки (x
, y
, z
), где определяется потенциал; V
- объем пространства, в котором распределен заряд.
Потенциал и работа сил электрического поля. Основываясь на определении потенциала, можно показать, что работа сил электрического поля при перемещении точечного заряда q из одной точки поля в другую равна произведению величины этого заряда на разность потенциалов в начальной и конечной точках пути, A = q (j 1 - j 2).
Определение удобно записать следующим образом:
Вопрос №4
Для установления связи между силовой характеристикой электрического поля - напряжённостью и его энергетической характеристикой - потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q : dA = q E dl , эта же работа равна убыли потенциальной энергии заряда q : dA = - dW п = - q d ,где d - изменение потенциала электрического поля на длине перемещения dl . Приравнивая правые части выражений, получаем: E dl = -d или в декартовой системе координат
E x dx + E y dy + E z dz = -d , (1.8)
где E x , E y , E z - проекции вектора напряженности на оси системы координат. Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем
![]() откуда .
откуда .
Стоящее в скобках выражение является градиентом потенциала j, т. е.
E = - grad = -Ñ .
Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком . Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.
Рассмотрим электрическое поле, создаваемое положительным точечным зарядом q (рис. 1.6). Потенциал поля в точке М , положение которой определяется радиус-вектором r , равен = q / 4pe 0 er . Направление радиус-вектора r совпадает с направлением вектора напряженности E , а градиент потенциала направлен в противоположную сторону. Проекция градиента на направление радиус-вектора
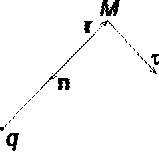
![]() . Проекция же градиента потенциала на направление вектора t
, перпендикулярного вектору r
, равна
. Проекция же градиента потенциала на направление вектора t
, перпендикулярного вектору r
, равна ![]() ,
,
т. е. в этом направлении потенциал электрического поля является постоянной величиной ( = const).
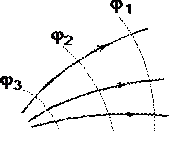 В рассмотренном случае направление вектора r
совпадает с направлением
В рассмотренном случае направление вектора r
совпадает с направлением
силовых линий. Обобщая полученный результат, можно утверждать, что во всех точках кривой, ортогональной к силовым линиям, потенциал электрического поля одинаков
. Геометрическим местом точек с одинаковым потенциалом является эквипотенциальная поверхность, ортогональная к силовым линиям.
При графическом изображении электрических полей часто используют эквипотенциальные поверхности. Обычно эквипотенциали проводят таким образом, чтобы разность потенциалов между любыми двумя эквипотенциальными поверхностями была одинакова. Здесь приведена двухмерная картина электрического поля. Силовые линии показаны сплошными линиями, эквипотенциали - штриховыми.
Подобное изображение позволяет сказать, в какую сторону направлен вектор напряжённости электрического поля; где напряжённость больше, где меньше; куда начнёт двигаться электрический заряд, помещённый в ту или иную точку поля. Так как все точки эквипотенциальной поверхности находятся при одинаковом потенциале, то перемещение заряда вдоль нее не требует работы. Это значит, что сила, действующая на заряд, все время перпендикулярна перемещению.
Вопрос №5
Если проводнику сообщить избыточный заряд, то этот заряд распределится по поверхности проводника . Действительно, если внутри проводника выделить произвольную замкнутую поверхность S , то поток вектора напряженности электрического поля через эту поверхность должен быть равен нулю. В противном случае внутри проводника будет существовать электрическое поле, что приведет к перемещению зарядов. Следовательно, для того, чтобы выполнялось условие
Суммарный электрический заряд внутри этой произвольной поверхности должен равняться нулю.
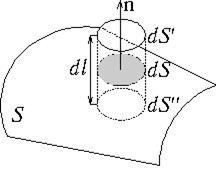
Напряженность электрического поля вблизи поверхности заряженного проводника можно определить, используя теорему Гаусса. Для этого выделим на поверхности проводника малую произвольную площадку dS
и, считая ее за основание, построим на ней цилиндр с образующей dl
(рис. 3.1). На поверхности проводника вектор Е
направлен по нормали к этой поверхности. Поэтому поток вектора Е
через боковую поверхность цилиндра из-за малости dl
равен нулю. Поток этого вектора через нижнее основание цилиндра, находящееся внутри проводника, также равен нулю, так как внутри проводника электрическое поле отсутствует. Следовательно, поток вектора Е
через всю поверхность цилиндра равен потоку через его верхнее основание dS "
: , где Е n - проекция вектора напряженности электрического поля на внешнюю нормаль n
к площадке dS
. 
По теореме Гаусса, этот поток равен алгебраической сумме электрических зарядов, охватываемых поверхностью цилиндра, отнесенной к произведению электрической постоянной и относительной диэлектрической проницаемости среды, окружающей проводник. Внутри цилиндра находится заряд , где - поверхностная плотность зарядов. Следовательно ![]() и , т. е. напряженность электрического поля вблизи поверхности заряженного проводника прямо пропорциональна поверхностной плотности электрических зарядов, находящихся на этой поверхности.
и , т. е. напряженность электрического поля вблизи поверхности заряженного проводника прямо пропорциональна поверхностной плотности электрических зарядов, находящихся на этой поверхности.
Экспериментальные исследования распределения избыточных зарядов на проводниках различной формы показали, что распределение зарядов на внешней поверхности проводника зависит только от формы поверхности : чем больше кривизна поверхности (чем меньше радиус кривизны), тем больше поверхностная плотность заряда.
Вблизи участков с малыми радиусами кривизны, особенно около острия, из-за высоких значений напряженности происходит ионизация газа, например, воздуха. В результате одноименные с зарядом проводника ионы движутся в направлении от поверхности проводника, а ионы противоположного знака к поверхности проводника, что приводит к уменьшению заряда проводника. Это явление получило название стекания заряда .
На внутренних поверхностях замкнутых полых проводников избыточные заряды отсутствуют .
Если заряженный проводник привести в соприкосновение с внешней поверхностью незаряженного проводника, то заряд будет перераспределяться между проводниками до тех пор, пока их потенциалы не станут равными.
Если же тот же заряженный проводник касается внутренней поверхности полого проводника, то заряд передается полому проводнику полностью.
В заключение отметим еще одно явление, присущее только проводникам. Если незаряженный проводник поместить во внешнее электрическое поле, то его противоположные части в направлении поля будут иметь заряды противоположных знаков. Если, не снимая внешнего поля, проводник разделить, то разделенные части будут иметь разноименные заряды. Это явление получило название электростатической индукции
.
Вопрос №8
Все вещества в соответствии с их способностью проводить электрический ток подразделяются на проводники
, диэлектрики
и полупроводники
. Проводниками называют вещества, в которых электрически заряженные частицы - носители заряда
- способны свободно перемещаться по всему объему вещества. К проводникам относятся металлы, растворы солей, кислот и щелочей, расплавленные соли, ионизированные газы.
Ограничим рассмотрение твердыми металлическими проводниками
, имеющими кристаллическую структуру
. Эксперименты показывают, что при очень малой разности потенциалов, приложенной к проводнику, содержащиеся в нем электроны проводимости, приходят в движение и перемещаются по объему металлов практически свободно.
В отсутствие внешнего электростатического поля электрические поля положительных ионов и электронов проводимости взаимно скомпенсированы, так что напряженность внутреннего результирующего поля равна нулю.
При внесении металлического проводника во внешнее электростатическое поле с напряженностью Е 0
на ионы и свободные электроны начинают действовать кулоновские силы, направленные в противоположные стороны. Эти силы вызывают смещение заряженных частиц внутри металла, причем в основном смещаются свободные электроны, а положительные ионы, находящиеся в узлах кристаллической решетки, практически не меняют своего положения. В результате внутри проводника возникает электрическое поле с напряженностью Е "
.
Смещение заряженных частиц внутри проводника прекращается тогда, когда суммарная напряженность поля Е
в проводнике, равная сумме напряженностей внешнего и внутреннего полей, станет равной нулю: ![]()
Представим выражение, связывающее напряженность и потенциал электростатического поля, в следующем виде:
где Е
- напряженность результирующего поля внутри проводника; n
- внутренняя нормаль к поверхности проводника. Из равенства нулю результирующей напряженности Е
следует, что в пределах объема проводника потенциал имеет одно и то же значение
: .
Полученные результаты позволяют сделать три важных вывода:
1. Во всех точках внутри проводника напряженность поля , т. е. весь объем проводника эквипотенциален
.
2. При статическом распределении зарядов по проводнику вектор напряженности Е
на его поверхности должен быть направлен по нормали к поверхности , в противном случае под действием касательной к поверхности проводника компоненты напряженности заряды должны перемещаться по проводнику.
3. Поверхность проводника также эквипотенциальна, так как для любой точки поверхности
![]()
Вопрос №10
Если два проводника имеют такую форму, что создаваемое ими электрическое поле сосредоточено в ограниченной области пространства, то образованная ими система носит название конденсатора
, а сами проводники называют обкладками
конденсатора.
Сферический конденсатор.
Два проводника, имеющие форму концентрических сфер с радиусами R
1 и R
2 (R
2 > R
1), образуют сферический конденсатор. Используя теорему Гаусса, легко показать, что электрическое поле существует только в пространстве между сферами. Напряженность этого поля ![]() ,
,
где q
- электрический заряд внутренней сферы; - относительная диэлектрическая проницаемость среды, заполняющей пространство между обкладками; r
- расстояние от центра сфер, причем R
1 r R
2 . Разность потенциалов между обкладками  и емкость сферического конденсатора .
и емкость сферического конденсатора .
Цилиндрический конденсатор
представляет собой два проводящих коаксиальных цилиндра радиусами R
1 и R
2 (R
2 > R
1). Пренебрегая краевыми эффектами на торцах цилиндров и считая, что пространство между обкладками заполнено диэлектрической средой с относительной проницаемостью , напряженность поля внутри конденсатора можно найти по формуле: ![]() ,
,
где q
- заряд внутреннего цилиндра; h
- высота цилиндров (обкладок); r
- расстояние от оси цилиндров. Соответственно, разность потенциалов между обкладками цилиндрического конденсатора и его емкость есть 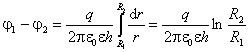 . .
. .
Плоский конденсатор.
Две плоские параллельные пластины одинаковой площади S
, расположенные на расстоянии d
друг от друга, образуют плоский конденсатор
. Если пространство между пластинами заполнено средой с относительной диэлектрической проницаемостью , то при сообщении им заряда q
напряженность электрического поля между пластинами равна , разность потенциалов равна . Таким образом, емкость плоского конденсатора .
Последовательное и параллельное соединение конденсаторов.
При последовательном соединении n конденсаторов суммарная емкость системы равна
Параллельное соединение n конденсаторов образует систему, электроемкость которой можно вычислить следующим образом:
Вопрос №11
Энергия заряженного проводника. Поверхность проводника является эквипотенциальной. Поэтому потенциалы тех точек, в которых находятся точечные заряды dq , одинаковы и равны потенциалу проводника. Заряд q , находящийся на проводнике, можно рассматривать как систему точечных зарядов dq . Тогда энергия заряженного проводника
Приняв во внимание определение емкости, можно записать
Любое из этих выражений определяет энергию заряженного проводника.
Энергия заряженного конденсатора.
Пусть потенциал обкладки конденсатора, на которой находится заряд +q
, равен , а потенциал обкладки, на которой находится заряд -q
, равен . Энергия такой системы
Энергию заряженного конденсатора можно представить в виде
Энергия электрического поля. Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает
Частное U
/ d
равно напряженности поля в зазоре; произведение S
·d
представляет собой объем V
, занимаемый полем. Следовательно, ![]()
Если поле однородно (что имеет место в плоском конденсаторе при расстоянии d много меньшем, чем линейные размеры обкладок), то заключенная в нем энергия распределяется в пространстве с постоянной плотностью w . Тогда объемная плотность энергии электрического поля равна
![]()
C учетом соотношения можно записать
В изотропном диэлектрике направления векторов D
и E
совпадают и
Подставим выражение , получим
Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика. Покажем это на примере неполярного диэлектрика. Поляризация неполярного диэлектрика заключается в том, что заряды, входящие в состав молекул, смещаются из своих положений под действием электрического поля Е . В расчете на единицу объема диэлектрика работа, затрачиваемая на смещение зарядов q i на величину dr i , составляет
Выражение в скобках есть дипольный момент единицы объема или поляризованность диэлектрика Р
. Следовательно, .
Вектор P
связан с вектором E
соотношением . Подставив это выражение в формулу для работы, получим
Проведя интегрирование, определим работу, затрачиваемую на поляризацию единицы объема диэлектрика .
Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенного в любом объеме V
. Для этого нужно вычислить интеграл: ![]()
Плотность энергии электростатического поля
Используя (66), (50), (53), преобразуем формулу для энергии конденсатора следующим образом: , где - объём конденсатора. Разделим последнее выражение на : ![]() . Величина имеет смысл плотности энергии электростатического поля.
. Величина имеет смысл плотности энергии электростатического поля.
Вопрос №12
Диэлектрик, помещенный во внешнее электрическое поле, поляризуется под действием этого поля. Поляризацией диэлектрика называется процесс приобретения им отличного от нуля макроскопического дипольного момента.
Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации (P ). Поляризованность определяется как электрический момент единицы объема диэлектрика,
 где N
- число молекул в объеме . Поляризованность P
часто называют поляризацией, понимая под этим количественную меру этого процесса.
где N
- число молекул в объеме . Поляризованность P
часто называют поляризацией, понимая под этим количественную меру этого процесса.
В диэлектриках различают следующие типы поляризации: электронную, ориентационную и решеточную (для ионных кристаллов).
Электронный тип поляризации
характерен для диэлектриков с неполярными молекулами. Во внешнем электрическом поле положительные заряды внутри молекулы смещаются по направлению поля, а отрицательные в противоположном направлении, в результате чего молекулы приобретают дипольный момент, направленный вдоль внешнего поля
 Индуцированный дипольный момент молекулы пропорционален напряженности внешнего электрического поля , где - поляризуемость молекулы. Значение поляризованности в этом случае равно , где n
- концентрация молекул ; - индуцированный дипольный момент молекулы, который одинаков для всех молекул и направление которого совпадает с направлением внешнего поля.
Индуцированный дипольный момент молекулы пропорционален напряженности внешнего электрического поля , где - поляризуемость молекулы. Значение поляризованности в этом случае равно , где n
- концентрация молекул ; - индуцированный дипольный момент молекулы, который одинаков для всех молекул и направление которого совпадает с направлением внешнего поля.
Ориентационнный тип поляризации
характерен для полярных диэлектриков. В отсутствие внешнего электрического поля молекулярные диполи ориентированы случайным образом, так что макроскопический электрический момент диэлектрика равен нулю.
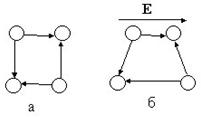 Если поместить такой диэлектрик во внешнее электрическое поле, то на молекулу-диполь будет действовать момент сил (рис. 2.2), стремящийся ориентировать ее дипольный момент в направлении напряженности поля. Однако полной ориентации не происходит, поскольку тепловое движение стремится разрушить действие внешнего электрического поля.
Если поместить такой диэлектрик во внешнее электрическое поле, то на молекулу-диполь будет действовать момент сил (рис. 2.2), стремящийся ориентировать ее дипольный момент в направлении напряженности поля. Однако полной ориентации не происходит, поскольку тепловое движение стремится разрушить действие внешнего электрического поля.
Такая поляризация называется ориентационной. Поляризованность в этом случае равна , где <p
> - среднее значение составляющей дипольного момента молекулы в направлении внешнего поля.
Решеточный тип поляризации
характерен для ионных кристаллов. В ионных кристаллах (NaCl и т.д.) в отсутствие внешнего поля дипольный момент каждой элементарной ячейки равен нулю (рис. 2.3.а), под влиянием внешнего электрического поля положительные и отрицательные ионы смещаются в противоположные стороны (рис. 2.3.б). Каждая ячейка кристалла становится диполем, кристалл поляризуется. Такая поляризация называется решеточной
. Поляризованность и в этом случае можно определить как , где - значение дипольного момента элементарной ячейки, n
- число ячеек в единице объема.
Поляризованность изотропных диэлектриков любого типа связана с напряженностью поля соотношением , где - диэлектрическая восприимчивость диэлектрика.
Вопрос №13
Поляризованность среды обладает примечательным свойством: поток вектора поляризованности среды через произвольную замкнутую поверхность численно равен величине некомпенсированных "связанных" зарядов внутри этой поверхности, взятой с обратным знаком:
![]() (1). В локальной формулировке описываемое свойство описывается соотношением
(1). В локальной формулировке описываемое свойство описывается соотношением
(2) , где - объемная плотность "связанных" зарядов. Эти соотношения называют теоремой Гаусса для поляризованности среды (вектора поляризации) в интегральной и дифференциальной формах соответственно. Если теорема Гаусса для напряженности электрического поля является следствием закона Кулона в "полевой" форме, то теорема Гаусса для поляризованности является следствием определения этой величины.
Докажем соотношение (1), тогда соотношение (2) окажется справедливым в силу математической теоремы Остроградского-Гаусса.
Рассмотрим диэлектрик из неполярных молекул с объемной концентрацией последних, равной . Считаем, что под действием электрического поля положительные заряды сместились из положения равновесия на величину , а отрицательные - на величину . Каждая молекула приобрела электрический момент ![]() , а единичный объем приобрел электрический момент . Рассмотрим произвольную достаточно гладкую замкнутую поверхность в описываемом диэлектрике. Допустим, что поверхность проведена так, что в отсутствие электрического поля она "не пересекает" отдельные диполи, то есть положительный и отрицательный заряды, связанные с молекулярной структурой вещества, "компенсируют" друг друга.
, а единичный объем приобрел электрический момент . Рассмотрим произвольную достаточно гладкую замкнутую поверхность в описываемом диэлектрике. Допустим, что поверхность проведена так, что в отсутствие электрического поля она "не пересекает" отдельные диполи, то есть положительный и отрицательный заряды, связанные с молекулярной структурой вещества, "компенсируют" друг друга.
Заметим, кстати, что соотношения (1) и (2) при и удовлетворяются тождественно.
Под действием электрического поля элемент площади поверхности пересекут положительные заряды из объема в количестве . Для отрицательных зарядов имеем соответственно величины и . Суммарный заряд, перешедший на "внешнюю" сторону элемента площади поверхности (напомним, что - внешняя нормаль к по отношению к охватываемому поверхностью объему) равен
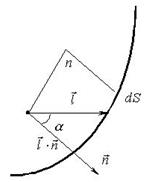
Свойства вектора поляризованности среды
Проинтегрировав полученное выражение по замкнутой поверхности , получим величину суммарного электрического заряда, покинувшего рассматриваемый объем. Последнее позволяет заключить, что в рассматриваемом объеме остался некомпенсированный заряд - , равный по модулю ушедшему заряду. В итоге имеем: ![]() , таким образом теорема Гаусса для векторного поля в интегральной формулировке доказана.
, таким образом теорема Гаусса для векторного поля в интегральной формулировке доказана.
Чтобы рассмотреть случай вещества, состоящего из полярных молекул, достаточно в приведенных выше рассуждениях величину заменить на ее среднее значение .
Доказательство справедливости соотношения (1) можно считать законченным.
Вопрос №14
В диэлектрической среде могут присутствовать электрические заряды двух типов: "свободные" и "связанные". Первые из них не связаны с молекулярной структурой вещества и, как правило, могут относительно свободно перемещаться в пространстве. Вторые связаны с молекулярной структурой вещества и под действием электрического поля могут смещаться из положения равновесия, как правило, на очень малые расстояния.
Использование напрямую теоремы Гаусса для векторного поля при описании диэлектрической среды неудобно тем, что правая часть формулы
![]() (1), содержит как величину "свободного", так и величину "связанного" (некомпенсированного) зарядов внутри замкнутой поверхности .
(1), содержит как величину "свободного", так и величину "связанного" (некомпенсированного) зарядов внутри замкнутой поверхности .
Если соотношение (1) почленно сложить с соотношением ![]() , получим
, получим ![]() , (2)
, (2)
где - суммарный "свободный" заряд объема, охватываемого замкнутой поверхность . Соотношение (2) обуславливает целесообразность введения специального вектора
В качестве удобной расчетной величины, характеризующей электрическое поле в диэлектрической среде. Вектор раньше называли вектором электрической индукции или вектором электрического смещения. В настоящее время входит в употребление термин "вектор ". Для векторного поля справедлива интегральная форма теоремы Гаусса: ![]() и, соответственно, дифференциальная форма теоремы Гаусса:
и, соответственно, дифференциальная форма теоремы Гаусса:
где - объемная плотность свободных зарядов.
Если справедливо соотношение (для жестких электретов оно не справедливо), то для вектора из определения (3) следует ,
где - диэлектрическая проницаемость среды, одна из важнейших электрических характеристик вещества. В электростатике и квазистационарной электродинамике величина является действительной. При рассмотрении высокочастотных колебательных процессов фаза колебания вектора , а значит и вектора , может не совпадать с фазой колебаний вектора , в таких случаях величина становится комплекснозначной величиной.
Рассмотрим вопрос, при каких условиях в диэлектрической среде возможно появление некомпенсированной объемной плотности связанных зарядов. Для этой цели запишем выражение вектора поляризации через диэлектрическую проницаемость среды и вектор :
В справедливости которого легко убедиться. Теперь представляющая интерес величина может быть вычислена:
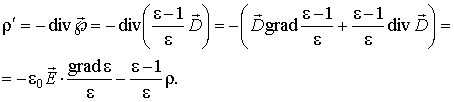 (3)
(3)
В отсутствие в диэлектрической среде объемной плотности свободных зарядов величина может обратиться в нуль, если
а) отсутствует поле ; или б) среда однородна или в) векторы и - ортогональны. В общем случае необходимо вычислить величину по соотношениям (3).
Вопрос №17
 Рассмотрим поведение векторов E
и D
на границе раздела двух однородных изотропных диэлектриков с проницаемостями и при отсутствии на границе свободных зарядов.
Рассмотрим поведение векторов E
и D
на границе раздела двух однородных изотропных диэлектриков с проницаемостями и при отсутствии на границе свободных зарядов.
Граничные условия для нормальных составляющих векторов D и E
следуют из теоремы Гаусса. Выделим вблизи границы раздела замкнутую поверхность в виде цилиндра, образующая которого перпендикулярна к границе раздела, а основания находятся на равном расстоянии от границы.
Так как на границе раздела диэлектриков нет свободных зарядов, то, в соответствии с теоремой Гаусса, поток вектора электрической индукции через данную поверхность
Выделяя потоки через основания и боковую поверхность цилиндра
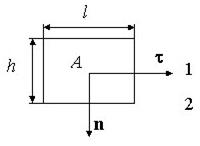 , где - значение касательной составляющей усредненное по боковой поверхности . Переходя к пределу при (при этом также стремится к нулю), получаем
, где - значение касательной составляющей усредненное по боковой поверхности . Переходя к пределу при (при этом также стремится к нулю), получаем ![]() , или окончательно для нормальных составляющих вектора электрической индукции . Для нормальных составляющих вектора напряженности поля получим
, или окончательно для нормальных составляющих вектора электрической индукции . Для нормальных составляющих вектора напряженности поля получим ![]() . Таким образом, при переходе через границу раздела диэлектрических сред нормальная составляющая вектора терпит разрыв
, а нормальная составляющая вектора непрерывна
.
. Таким образом, при переходе через границу раздела диэлектрических сред нормальная составляющая вектора терпит разрыв
, а нормальная составляющая вектора непрерывна
.
Граничные условия для касательных составляющих векторов D и E
следуют из соотношения, описывающего циркуляцию вектора напряженности электрического поля. Построим вблизи границы раздела прямоугольный замкнутый контур длины l
и высоты h
. Учитывая, что для электростатического поля , и обходя контур по часовой стрелке, представим циркуляцию вектора E
в следующем виде: ![]() ,
,
где - среднее значение E n на боковых сторонах прямоугольника. Переходя к пределу при , получим для касательных составляющих E .
Для касательных составляющих вектора электрической индукции граничное условие имеет вид ![]()
 Таким образом, при переходе через границу раздела диэлектрических сред касательная составляющая вектора непрерывна
, а касательная составляющая вектора терпит разрыв
.
Таким образом, при переходе через границу раздела диэлектрических сред касательная составляющая вектора непрерывна
, а касательная составляющая вектора терпит разрыв
.
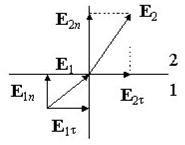
Преломление линий электрического поля.
Из граничных условий для соответствующих составляющих векторов E
и D
следует, что при переходе через границу раздела двух диэлектрических сред линии этих векторов преломляются (рис. 2.8). Разложим векторы E 1
и E 2
у границы раздела на нормальные и тангенциальные составляющие и определим связь между углами и при условии . Легко видеть, что как для напряженности поля, так и для индукции справедлив один и тот же закон преломления линий напряженности и линий смещения
![]() .
.
При переходе в среду с меньшим значением угол, образуемый линиями напряженности (смещения) с нормалью, уменьшается, следовательно, линии располагаются реже. При переходе в среду с большей линии векторов E
и D
, напротив, сгущаются и удаляются от нормали
.
Вопрос №6
Теорема о единственности решения задач электростатики (заданы расположения проводников и их заряды).
Если задано расположение проводников в пространстве и полный заряд каждого из проводников, то вектор напряжённости электростатического поля в каждой точке определяется единственным образом. Док-во: (от противного)
Пусть заряд на проводниках распределён следующим образом:
Предположим, что возможно не только такое, но и отличное от него распределение зарядов:
(то есть отличается сколь угодно мало хотя бы на одном проводнике)
Значит хотя бы в одной точке пространства отыщется иной вектор E, т.е. вблизи новых значений плотности по крайней мере в каких-то точках E будет отлично. Т.о. при тех же самых начальных условиях, при тех же самых проводниках получим другое решение. Теперь поменяем знак заряда на противоположный.
(менять знак надо сразу на всех проводниках)
Вид силовых линий при этом не изменится (не противоречит ни теореме Гаусса, ни теореме о циркуляции), изменится только их направление и вектора E.
Теперь возьмём суперпозицию зарядов (комбинацию двух вариантов зарядов):
(т.е. наложим один заряд на другой, и зарядим уже 3-им способом)
Если не совпадает хотя бы где-то с , то хотя бы в одном месте получим какое-то
 3) уводим линии в бесконечность, не замыкая их на проводнике. при этом замкнутый контур L замыкаем на бесконечности. Но и вэтом случае обход по силовой линии не даст нулевой циркуляции.
3) уводим линии в бесконечность, не замыкая их на проводнике. при этом замкнутый контур L замыкаем на бесконечности. Но и вэтом случае обход по силовой линии не даст нулевой циркуляции.
Вывод: значит не может быть какой-либо отличной о нуля, значит распределение зарядов установлено единственным образом –> единственность решения, т.е. E – находим единственным образом.
Вопрос №7
Билет 7. Теорема о единственности решения задач электростатики. (заданы расположения проводников и их потенциалы). Если задано расположение проводников и потенциал каждого из них, то напряжённость электростатического поля в каждой точке находится единственным образом.
(Берклеевский курс)
Всюду вне проводника функция должна удовлетворять дифференциальному уравнению в частных производных: , или, иначе, (2)
Очевидно, что W не удовлетворяет граничным условиям. У поверхности каждого проводника функция W равна нулю, так как и принимают одинаковое значение у поверхности проводника. Следовательно W является решением другой электростатической задачи, с теми же проводниками, но при условии, что все проводники имеют нулевой потенциал. Если это так, то можно утверждать, что функция W равна нулю во всех точках пространства. Если это не так, то она должна иметь где-то максимум или минимум. Путь W имеет экстремум в точке P, рассмотрим тогда шар с центром в этой точке. Нам известно, что среднее значение по сфере функции, удовлетворяющей уравнению Лапласа, равно значению функции в центре. Это несправедливо, если центр является максимум или минимумом этой функции. Таким образом, W не может иметь максимума или минимума, она всюду должна быть равна нулю. Отсюда следует, что =
Вопрос №28
 Трм. о циркуляции в-ра I
.
Трм. о циркуляции в-ра I
.
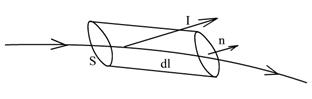
I – вектор намагниченности. I = = N p 1 м = Nn i 1 S \ c
DV = Sdl cosα; di мол = i 1 мол NSdl cosα = cIdl cosα, N – число мол-л на 1см 3 . Вблизи контура считаем вещество однородным, т.е все диполи, все молекулы имеют одинаковый магнитный момент. Для подсчета возьмем молекулу, я дро которой расположено прямо на контуре dl. Надо посчитать, сколько атомов пересекут цилиндрик 1 раз => Это такие, чьи центры лежат внутри этого самого воображ цилиндра. Таким образом нас интересует только i мол – т.е. ток, пересекающий поверхность, опирающуюся на контур.
Вопрос №9
1. Энергия системы точечных неподвижных зарядов . Электростатические силы консервативны и система зарядов обладает потенциальной энергией. Пусть заряды Q 1 и Q 2 находятся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией
где φ 12 и φ 21 – соответственно потенциалы, создаваемые зарядом Q 2 в точке нахождения заряда Q 1 , и наоборот.
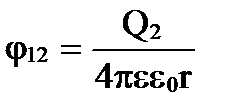 ;
; 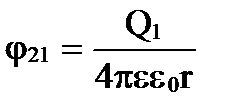 .
.
W 1 = W 2 =W = Q 1 φ 12 = Q 2 φ 21 = ½ (Q 1 φ 12 + Q 2 φ 21).
Добавляя к системе из двух зарядов последовательно заряды Q 3 , Q 4 , …, Q n , можно убедиться, что энергия взаимодействия системы зарядов равна
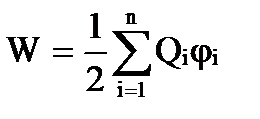 ,
,
где φ i – потенциал, создаваемый в той точке, где находится заряд Q i , всеми зарядами, кроме i-го.
2. Энергия заряженного уединенного проводника . Пусть имеется уединенный проводник, заряд, емкость и потенциал которого Q, C, φ.
Увеличим заряд на dQ. Для этого необходимо перенести заряд dQ из бесконечности к поверхности проводника, затратив на это работу, равную
dA = φdQ = C φd φ
Чтобы зарядить тело от нулевого потенциала до потенциала равного φ необходимо совершить работу
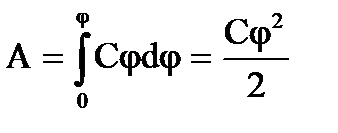
Энергия заряженного проводника будет равна этой работе

Учитывая, что  , эту энергию можно представить в виде
, эту энергию можно представить в виде
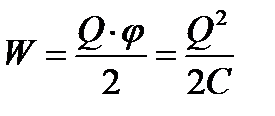
3. Энергия заряженного конденсатора . Как всякий заряженный проводник, конденсатор обладает энергией
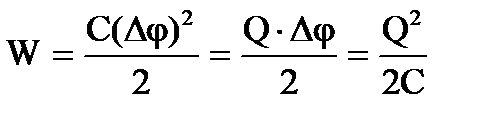
где Q - заряд конденсатора, С – его емкость и Δφ – разность потенциалов между обкладками.
Используя выражение для энергии, можно найти механическую (пондеромоторную) силу, с которой пластины конденсатора притягивают друг друга. Для этого предположим, что расстояние х между пластинами меняется на величину dx. Тогда действующая сила совершает работу равную
за счет уменьшения потенциальной энергии Fdx = - dW, откуда
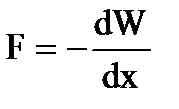 .
.
Подставляя в формулу энергии 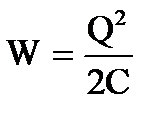 выражение емкости
выражение емкости
 , получим
, получим
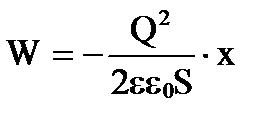 .
.
Дифференцируя W по х , найдем силу F
 ,
,
где знак “минус“ указывает, что сила F стремится уменьшить расстояние между пластинами, т.е. является силой притяжения. Подставляя выражение плотности зарядов на пластинках  , получим
, получим 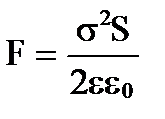 .
.
Учитывая напряжённость поля, что Е =  , получим
, получим
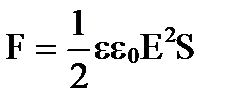 .
.
Давление на пластины диэлектрика, помещенные в зазоре конденсатора, будет
![]()
4. Энергия электростатического поля
.
Преобразуем формулу энергии плоского конденсатора  , используя формулы
, используя формулы
 и Δφ = Еd.
и Δφ = Еd.
Получим ,
где V – объем пространства между пластинами конденсатора, в котором сосредоточена энергия его поля W.
Объемную плотность энергии поля w – это энергия, заключённая в единице объёма электрического поля и она равна
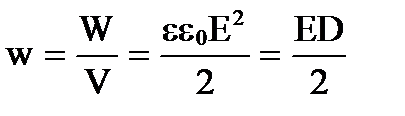 .
.
Единица измерения [Дж/м 3 ].
Видно, что объемная плотность энергии поля зависит только от характеристик поля и среды.

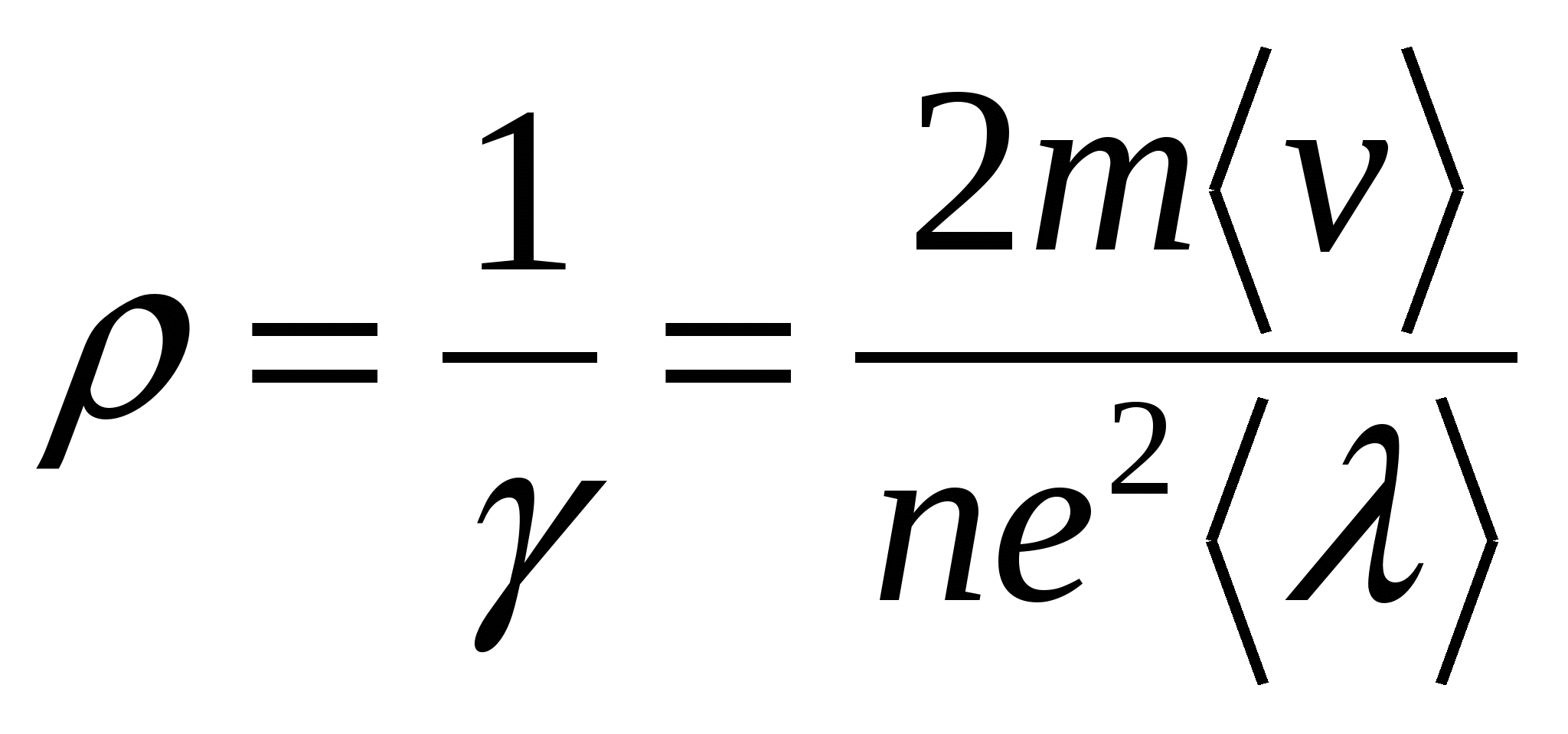 .
. . Эту энергию электрон полностью передает иону кристаллической решетки при столкновении с ним. Множество таких столкновений приводит к выделению джоулевой теплоты. Если концентрация электронов n
, и каждый из них сталкивается
. Эту энергию электрон полностью передает иону кристаллической решетки при столкновении с ним. Множество таких столкновений приводит к выделению джоулевой теплоты. Если концентрация электронов n
, и каждый из них сталкивается  раз за 1 с, то в единичном объеме проводника выделиться мощность
раз за 1 с, то в единичном объеме проводника выделиться мощность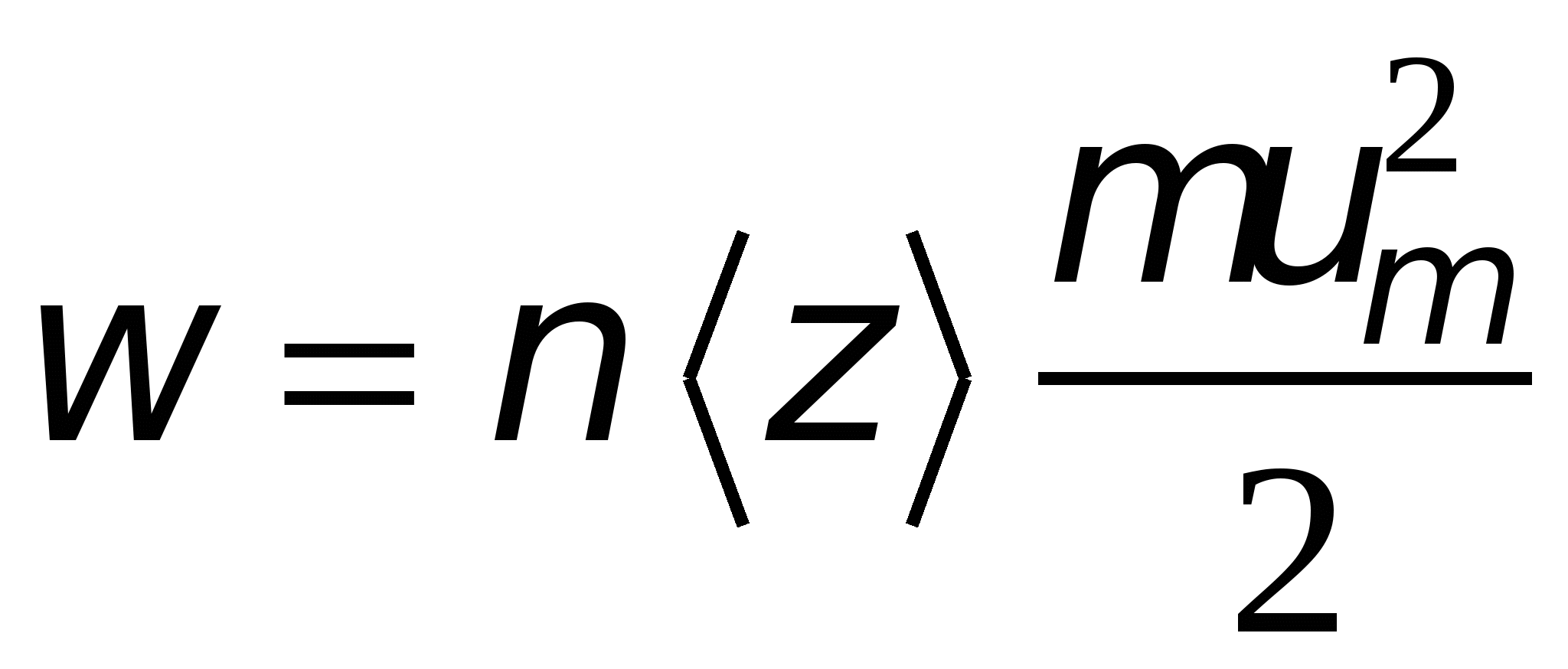 .
.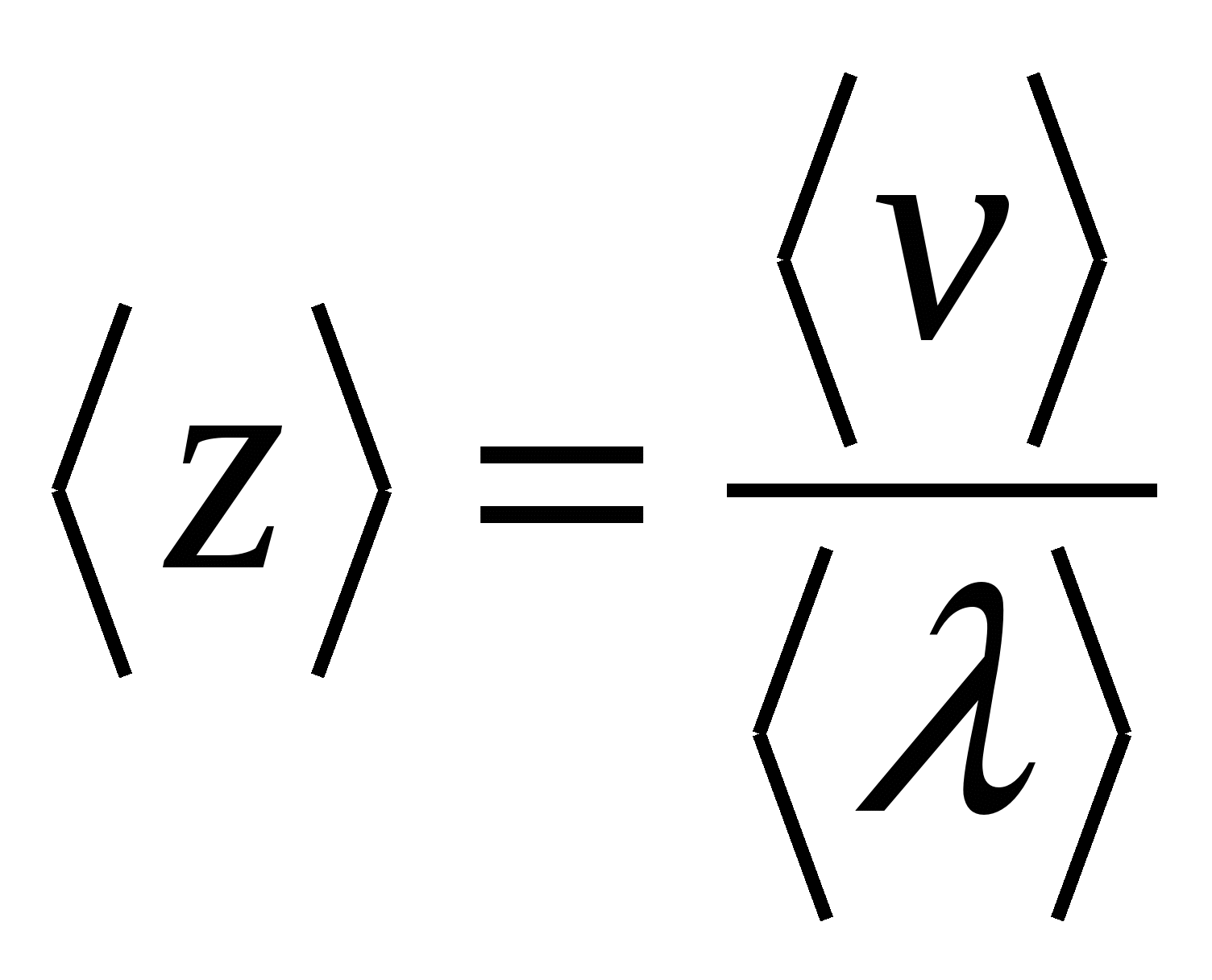 ,
, 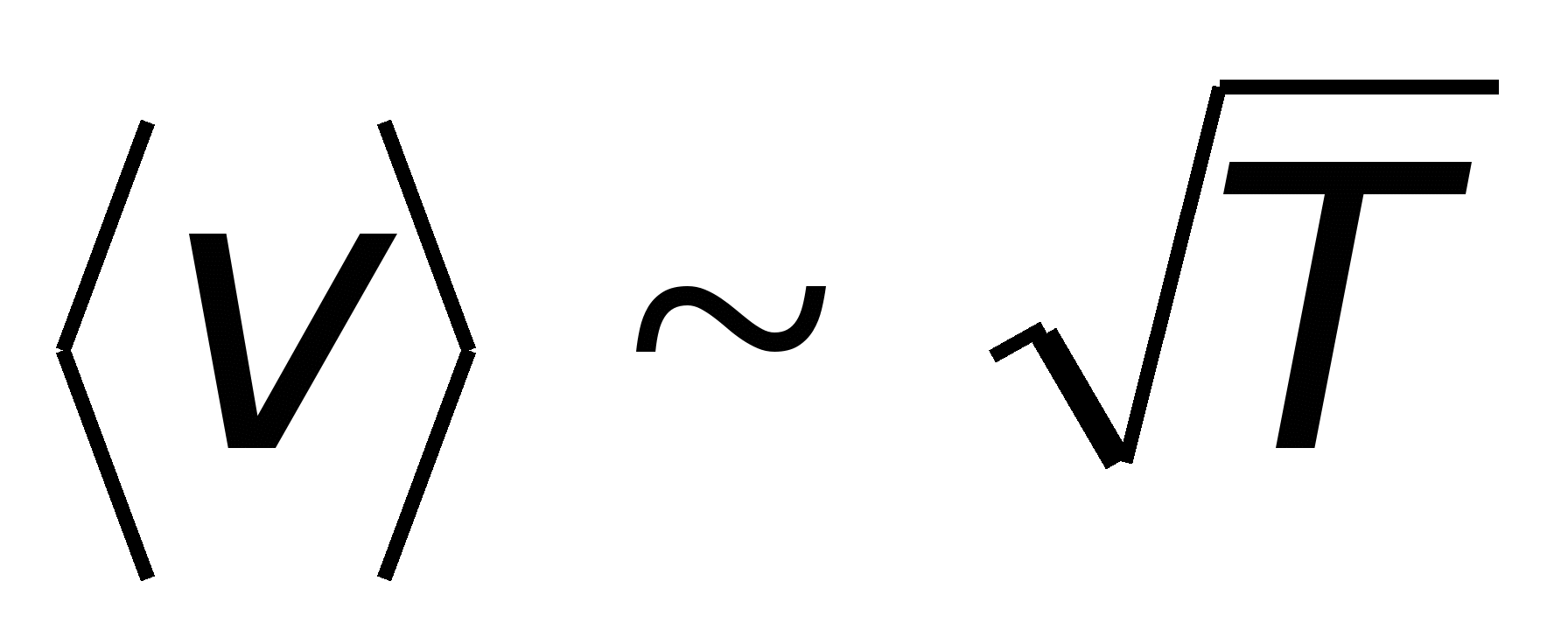 , следовательно, удельное сопротивление
, следовательно, удельное сопротивление 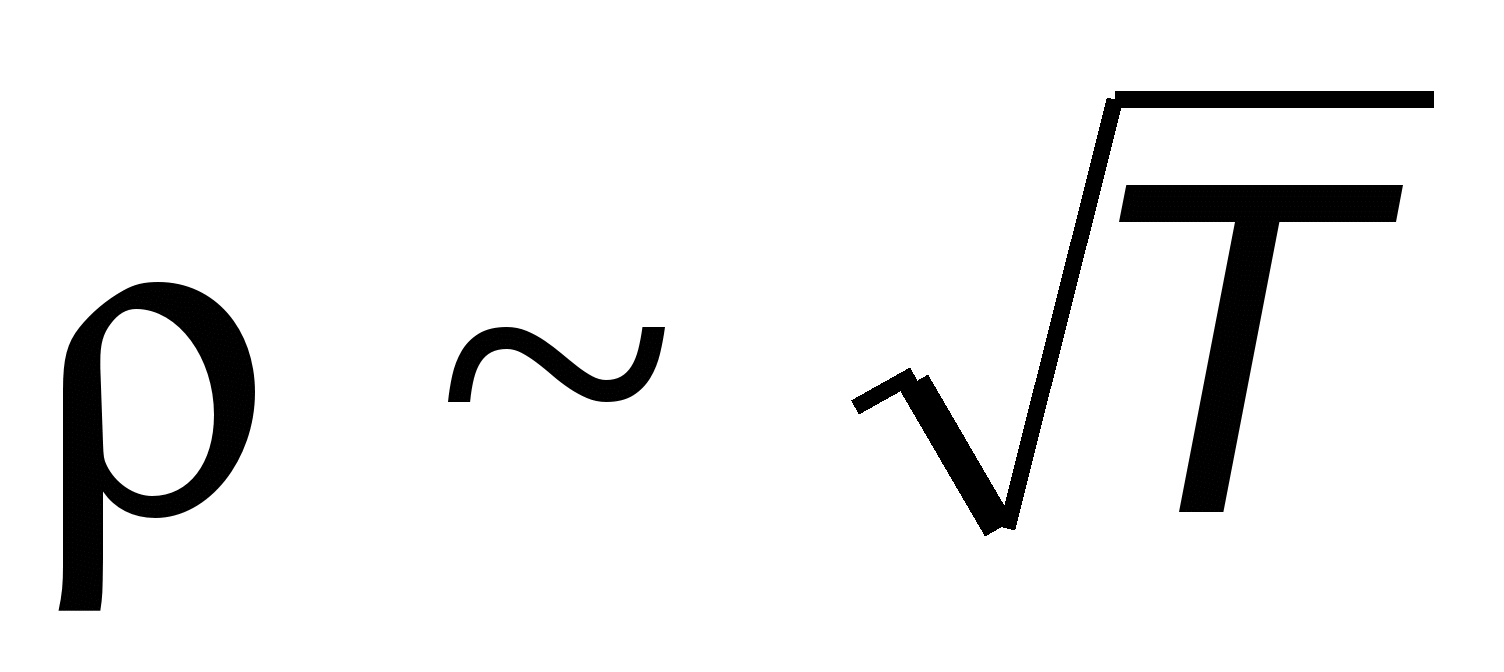 . Между тем опыт показывает, что линейно зависит от температуры
. Между тем опыт показывает, что линейно зависит от температуры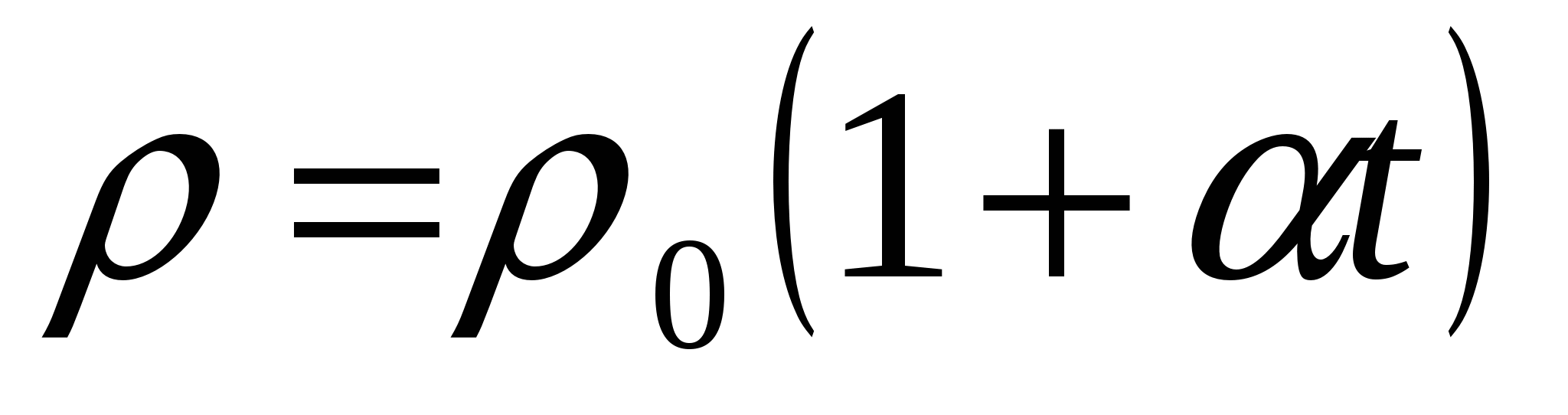 ,
,
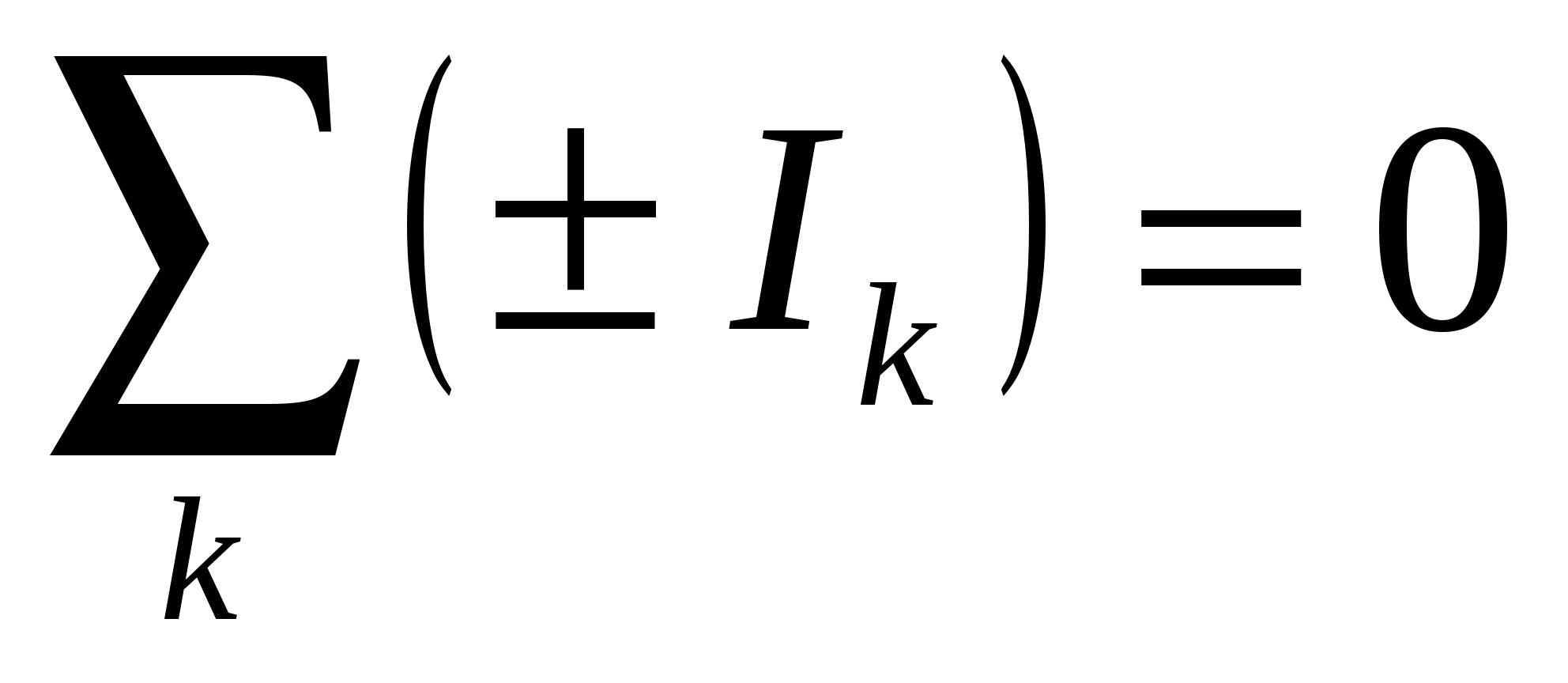 .
.
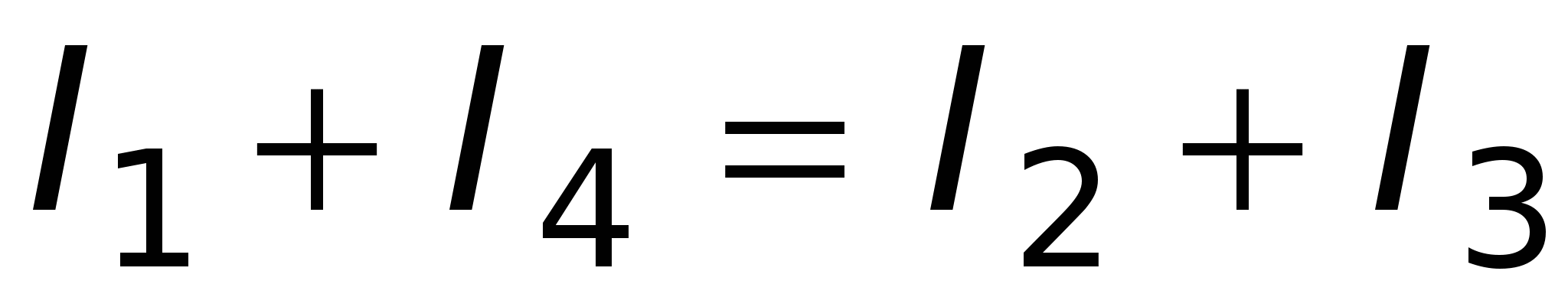 ,
,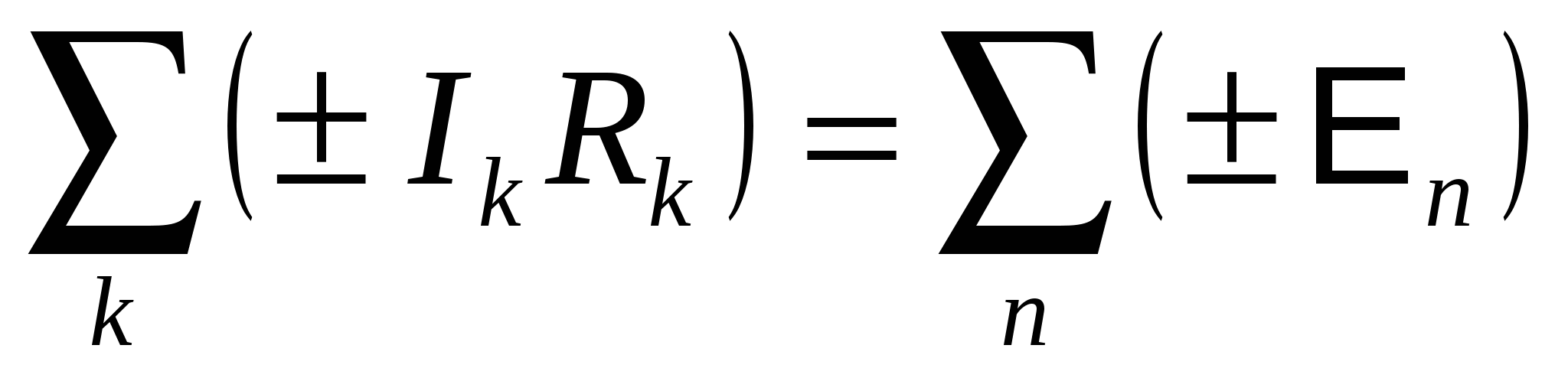 .
.