Zależność pomiędzy głównymi charakterystykami pola elektrostatycznego. Pole elektrostatyczne i ładunek jednostkowy
W społeczeństwie panuje stereotyp, według którego za materię można uznać jedynie to, co nie tylko istnieje realnie, ale i jest widoczne. tylko częściowo prawda. Jednym z najbardziej uderzających przykładów niewidzialnej materii jest pole elektrostatyczne. Jego szczególnym rodzajem są pola magnetyczne i elektryczne. Można to dość łatwo zweryfikować, jeśli weźmie się pod uwagę pole elektrostatyczne i jego charakterystykę.
Już w 1785 roku C. Coulomb odkrył i uzasadnił prawo dotyczące siły oddziaływania między dwoma ciałami punktowymi, które jednak nie było jasne, w jaki sposób dokładnie przenoszone jest uderzenie. Przeprowadzono szereg eksperymentów, w szczególności gdy ładunki znajdowały się w próżni. Prawo było szanowane. Pozwoliło nam to założyć, że do przeniesienia siły nie jest potrzebny zwykły ośrodek pośredni. Następnie J. Maxwell (na podstawie prac Faradaya) odkrył pole elektrostatyczne w próżni. Okazało się, że pole zawsze istnieje wokół ładunków, niezależnie od ich rodzaju środowisko i zapewnia ich interakcję.
Ponieważ pole jest materialne, „poddaje się” wzorom Einsteina i rozchodzi się z prędkością światła. Pole elektrostatyczne otrzymało swoją nazwę ze względu na swoją charakterystykę dla ładunków stacjonarnych („statyka” - spokój, równowaga). Siłę odkrytą przez Coulomba nazywa się elektryczną. Opisuje intensywność, z jaką pole oddziałuje na wprowadzony do niego ładunek.
Jedną z cech pola elektrostatycznego jest jego intensywność. Wskazuje stopień interakcji pomiędzy ładunkami punktowymi. Do badań wykorzystuje się tzw. ładunek próbny, którego wprowadzenie w pole nie powoduje jego zniekształcenia. Zwykle przyjmuje się, że jest to równe 1,6 * 10 do potęgi -19 kulombów. Jeśli napięcie jest oznaczone literą „E”, wówczas otrzymujemy:
gdzie F jest siłą działającą na ładunek jednostkowy Q (na przykład ładunek próbny). Stosowanie prawa Coulomba do obliczeń wymaga uwzględnienia współczynnika średniego.
Pole elektrostatyczne oddziałuje na dowolną liczbę ładunków i to tworzy złożony system interakcje. Natężenie pola systemu można rozpatrywać w kategoriach superpozycji, więc całkowity efekt liczby N ładunków jest sumą wektorową wszystkich natężeń pól. Nawiasem mówiąc, koncepcja „linii napięcia” (termin znany ze szkolnych zajęć z fizyki) powstała dzięki Faradaya, który schematycznie przedstawił pole za pomocą linii, które w każdym dowolnym punkcie pokrywały się z wektorami napięcia pole elektrostatyczne. Odpowiednio, im więcej takich linii, tym intensywniejsze jest oddziaływanie siły. W odróżnieniu od elektrostatyki linie naprężające nie są zamknięte. Warto również zauważyć, że w metalach (i innych materiałach przewodzących) nie ma natężenia pola na skutek przeciwnego działania pola wolnych nośników ładunku znajdujących się w strukturze sieci krystalicznej. W rzeczywistości siły szybko się wyrównują, nie ma prądu, a linie napięcia nie mogą przeniknąć przez taki przewodnik.
Dodatkowo pole można opisać wartościami skalarnymi pobranymi w każdym (idealnym przypadku) punkcie. W elektrostatyce określone wartości scharakteryzować potencjał pola. Można powiedzieć, że odpowiada ona wartości jednostkowego ładunku dodatniego w dowolnym punkcie pola. Odpowiednio, jednostką miary jest wolt. Jest ona określona przez stosunek energii potencjalnej ładunku sondy Q do jego wielkości, czyli sondy W / Q.
Sam potencjał jest równy pracy wykonanej przez siły pola elektrostatycznego, przenoszące ładunek z jednego punktu do drugiego, nieskończenie odległego.
TEORIA POLA
Teoria pola to badanie zjawisk elektrycznych i magnetycznych, zasad teoretycznych i praw, którym podlegają te zjawiska, oraz wynikających z nich metod obliczeniowych.
Pole elektromagnetyczne jest szczególnym rodzajem materii, jest nośnikiem energii i posiada specyficzne (wrodzone tylko jemu) właściwości elektryczne i magnetyczne. Przedstawimy podstawowe właściwości i metody obliczania pól w kolejności przejścia od prostszych do bardziej złożonych. Zgodnie z tym najpierw rozważymy pola stałe w czasie, a dopiero potem zbadamy zmienne pole elektromagnetyczne. Badanie wszystkich typów pól poszerza pojęcia fizyczne pola, znane na lekcjach fizyki, przyczynia się do głębszego zrozumienia procesów zachodzących w urządzeniach elektrycznych, jest ważne z praktycznego punktu widzenia, ponieważ pozwala rozwiązać wiele problemów o istotnym znaczeniu nie tylko dla teorii obwody elektryczne, ale także problemy bardziej ogólne (promieniowanie i odprowadzanie energii elektrycznej itp.).
Badać będziemy jedynie pola w ośrodkach jednorodnych (identycznych we wszystkich punktach pola) i izotropowych (o właściwościach niezależnych od natężenia pola).
Pole elektrostatyczne
Pole elektrostatyczne jest szczególnym przypadkiem pola elektromagnetycznego; jest ono tworzone przez ładunki, które są nieruchome w przestrzeni (w stosunku do obserwatora) i stałe w czasie. Pole elektrostatyczne nie oddziałuje bezpośrednio na zmysły człowieka, ma jednak wrodzoną zdolność oddziaływania siłą mechaniczną na umieszczony w nim ładunek testowy. Efekt ten jest podstawą do detekcji pola elektrostatycznego i określenia jego natężenia.
Głównymi wielkościami charakteryzującymi właściwości tego pola są jego natężenie i potencjał. Jeśli ładunek próbny zostanie umieszczony w polu elektrostatycznym na tyle małym, że jego obecność nie zniekształci go, wówczas zadziała na niego siła. Stosunek tej siły do wielkości ładunku określi natężenie pola 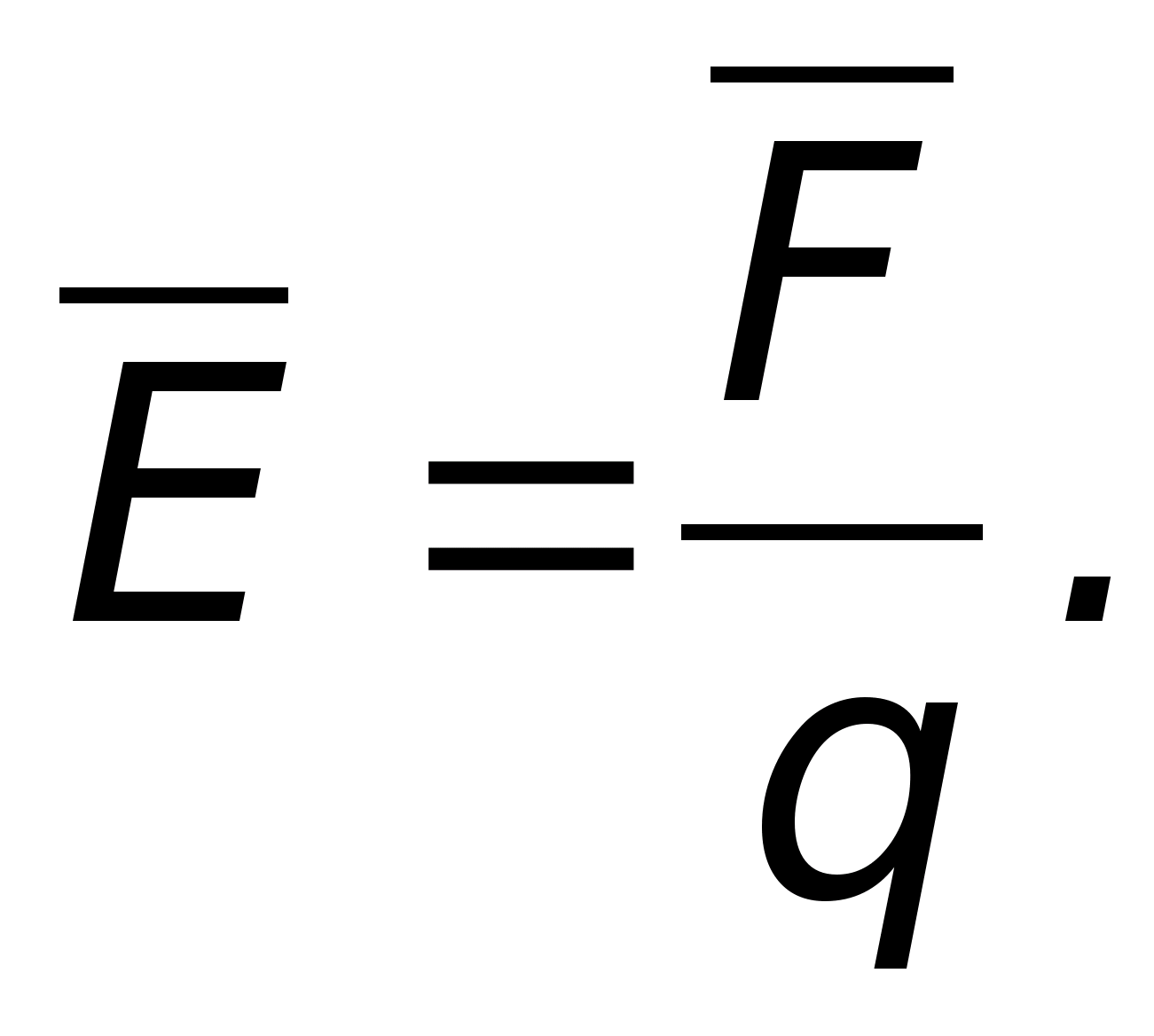 Jeśli
Jeśli 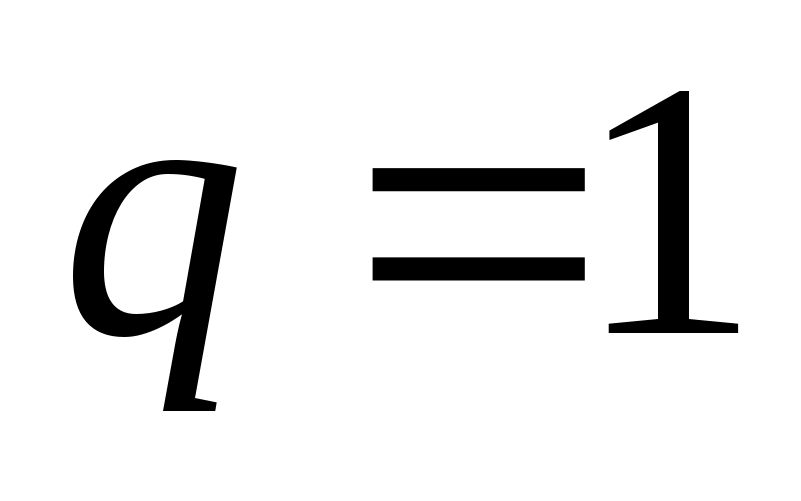 , To
, To  Wynika z tego, że natężenie pola jest równe sile działającej na jednostkowy ładunek dodatni i charakteryzuje natężenie pola; Jednostka napinająca
Wynika z tego, że natężenie pola jest równe sile działającej na jednostkowy ładunek dodatni i charakteryzuje natężenie pola; Jednostka napinająca
D  Pomińmy, że w pewnym polu elektrostatycznym pojedynczy dodatni ładunek próbny pod wpływem sił pola przemieszcza się z punktu 1 do punktu 2 (rys. 11.1). Następnie
Pomińmy, że w pewnym polu elektrostatycznym pojedynczy dodatni ładunek próbny pod wpływem sił pola przemieszcza się z punktu 1 do punktu 2 (rys. 11.1). Następnie  wykona pracę, aby przenieść ten ładunek z punktu 1 do punktu 2. Z kursu fizyki wiadomo, że praca wykonana podczas przemieszczania jednostkowego ładunku dodatniego z jednego punktu do drugiego to napięcie lub różnica potencjałów, tj.
wykona pracę, aby przenieść ten ładunek z punktu 1 do punktu 2. Z kursu fizyki wiadomo, że praca wykonana podczas przemieszczania jednostkowego ładunku dodatniego z jednego punktu do drugiego to napięcie lub różnica potencjałów, tj. 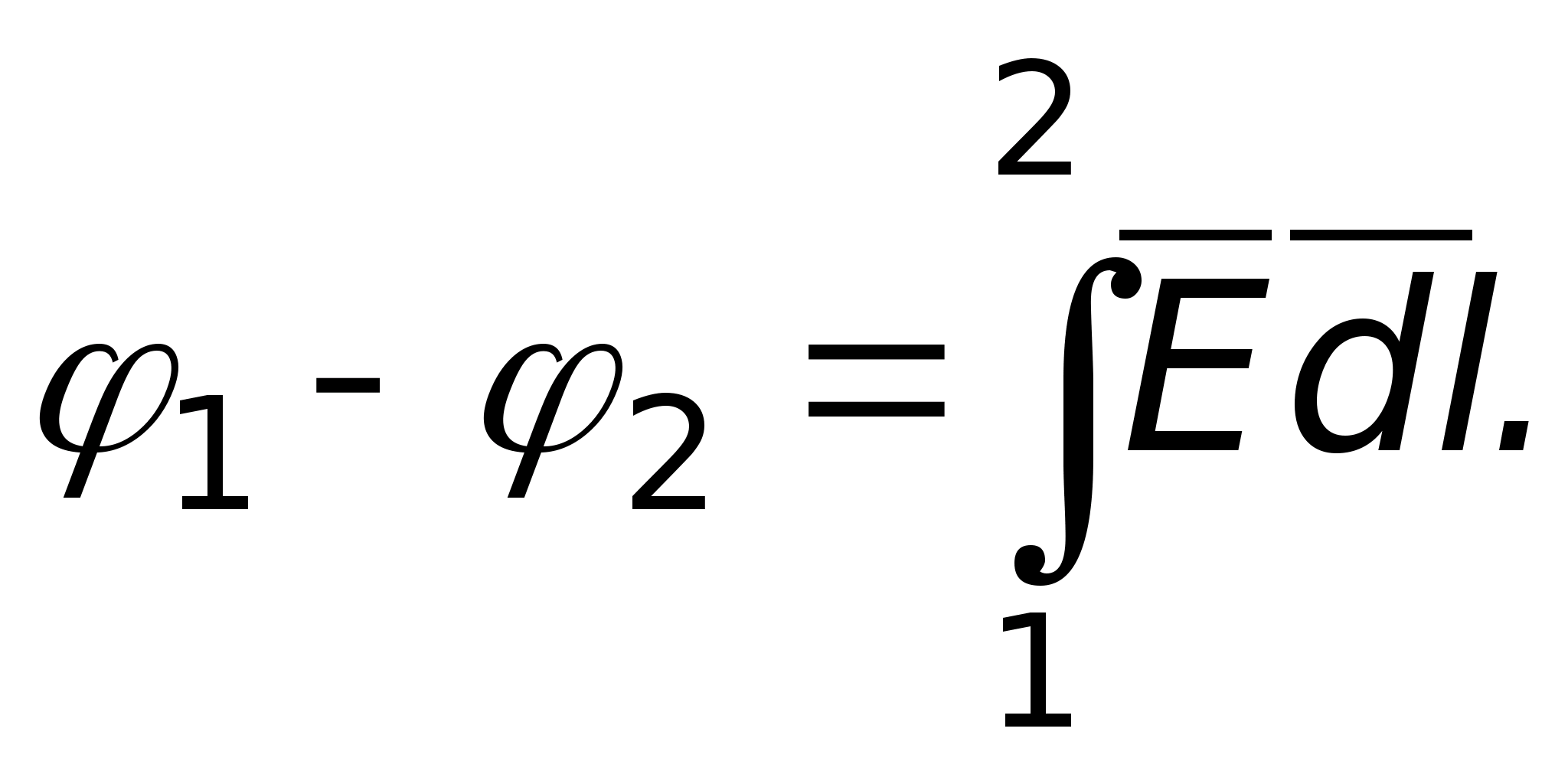 Jeśli
Jeśli 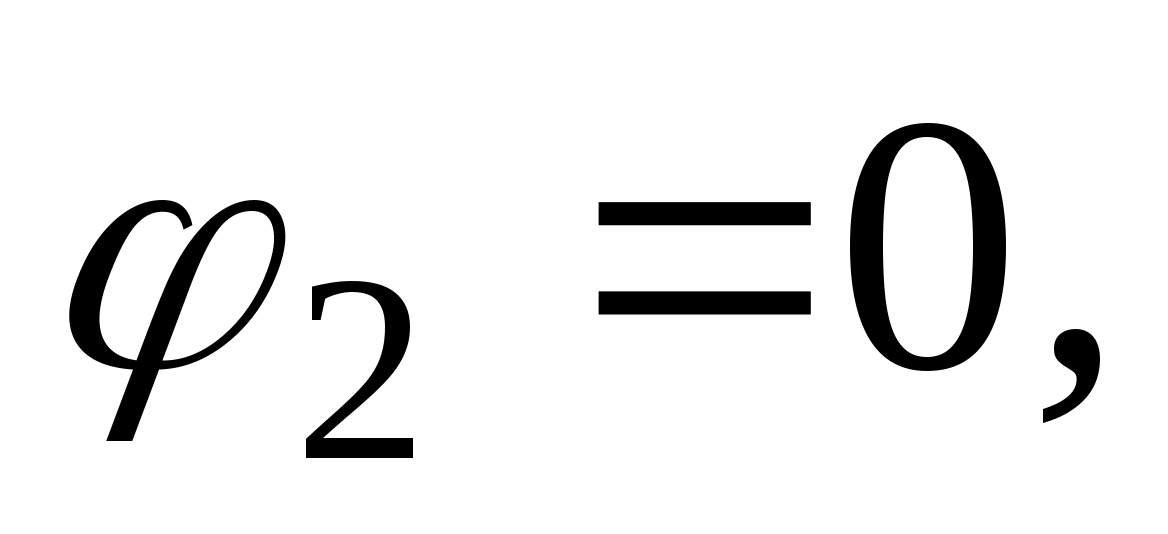 To
To 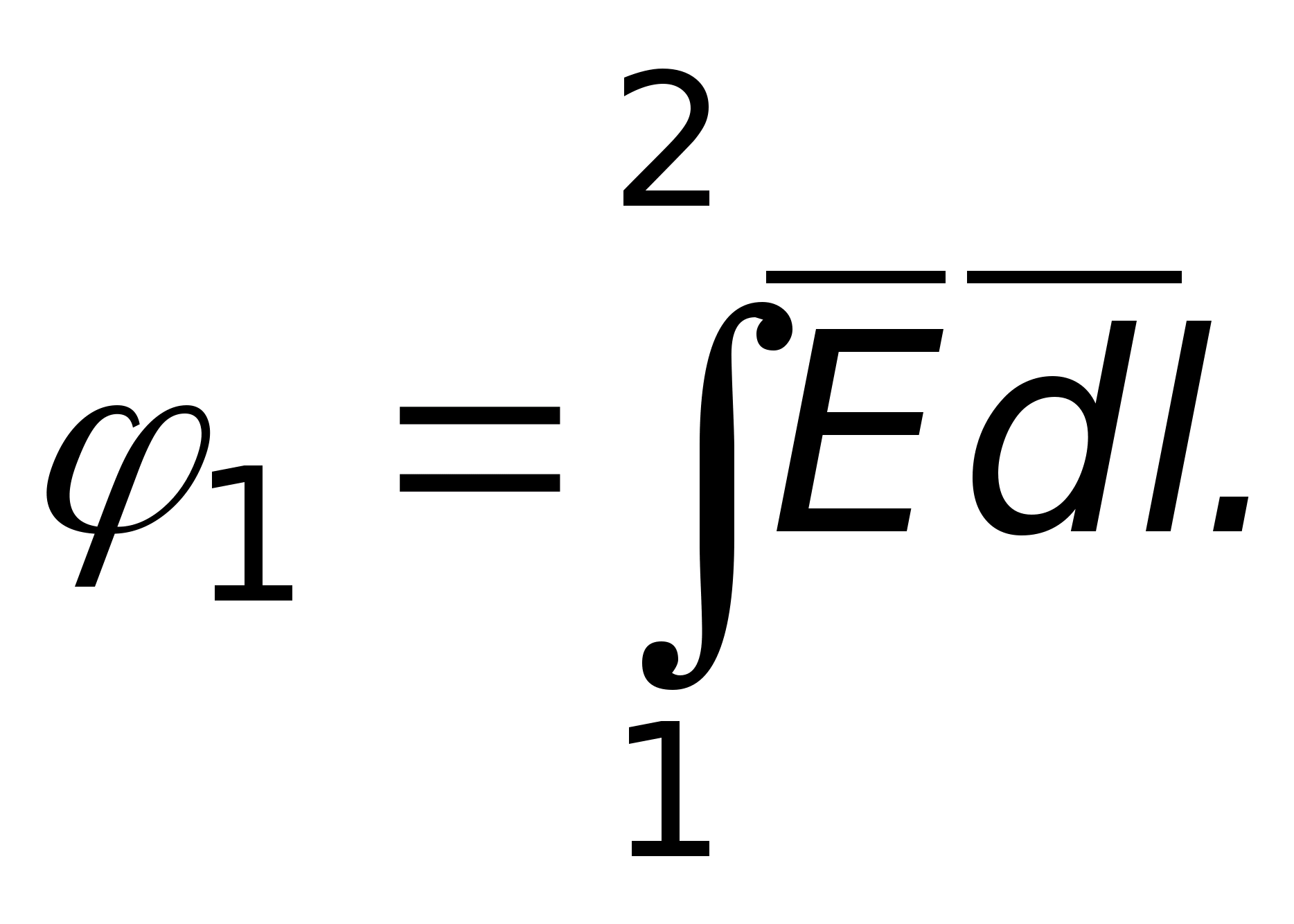 Wynika z tego, że potencjał pewnego punktu to praca wykonana w celu przeniesienia jednostkowego ładunku dodatniego z danego punktu do takiego, którego potencjał wynosi zero. Jako punkt o potencjale zerowym można wybrać dowolny punkt. Często umieszcza się go w nieskończoności, czasem na powierzchni ziemi. Jeśli zostanie wybrany punkt o potencjale zerowym, wówczas potencjały wszystkich pozostałych punktów zostaną całkowicie jednoznacznie określone. Z tego, co zostało rozważone, jasne jest, że potencjał jest określany z dokładnością do stałej, w zależności od tego, gdzie znajduje się punkt o potencjale zerowym. Pod tym względem związek między potencjałem a napięciem jest zapisany w następujący sposób:
Wynika z tego, że potencjał pewnego punktu to praca wykonana w celu przeniesienia jednostkowego ładunku dodatniego z danego punktu do takiego, którego potencjał wynosi zero. Jako punkt o potencjale zerowym można wybrać dowolny punkt. Często umieszcza się go w nieskończoności, czasem na powierzchni ziemi. Jeśli zostanie wybrany punkt o potencjale zerowym, wówczas potencjały wszystkich pozostałych punktów zostaną całkowicie jednoznacznie określone. Z tego, co zostało rozważone, jasne jest, że potencjał jest określany z dokładnością do stałej, w zależności od tego, gdzie znajduje się punkt o potencjale zerowym. Pod tym względem związek między potencjałem a napięciem jest zapisany w następujący sposób: 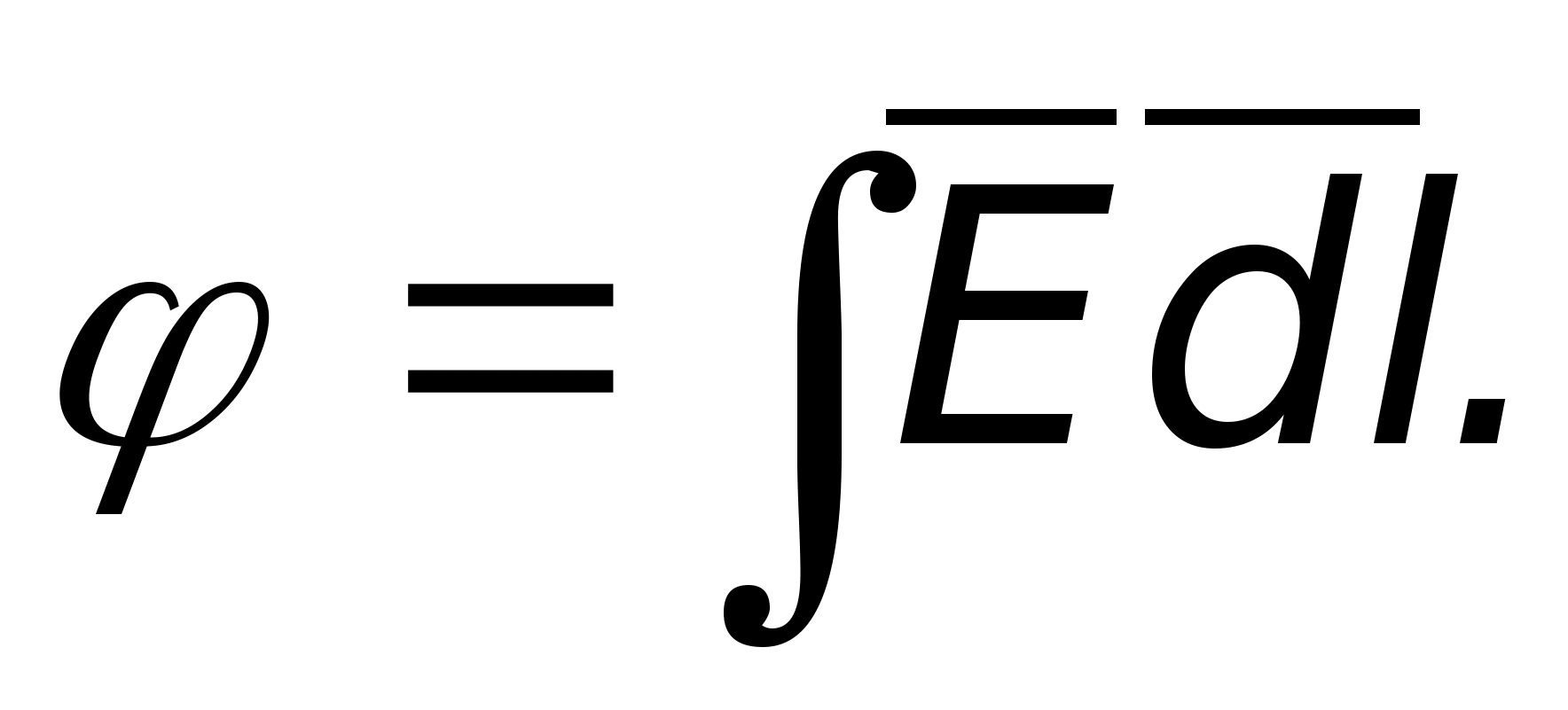 Fakt, że potencjał jest wyznaczany z dokładnością do stałej, nie ma praktycznego znaczenia, ponieważ Ważne jest napięcie, które jest równe różnicy potencjałów, a po jego przyjęciu stała całkowania ulega zniszczeniu.
Fakt, że potencjał jest wyznaczany z dokładnością do stałej, nie ma praktycznego znaczenia, ponieważ Ważne jest napięcie, które jest równe różnicy potencjałów, a po jego przyjęciu stała całkowania ulega zniszczeniu.
Jeśli  weź wzdłuż zamkniętego konturu, to da zero, tj.
weź wzdłuż zamkniętego konturu, to da zero, tj.  Oznacza to, że podczas poruszania się po zamkniętym konturze pewna ilość pracy jest wykonywana przez siły pola i dokładnie taka sama praca jest wykonywana przeciwko siłom pola. Stosunek
Oznacza to, że podczas poruszania się po zamkniętym konturze pewna ilość pracy jest wykonywana przez siły pola i dokładnie taka sama praca jest wykonywana przeciwko siłom pola. Stosunek  wyraża jedną z głównych właściwości pola elektrostatycznego - jest nim potencjał (potencjalne są wszystkie pola, dla których zachodzi podobna zależność - grawitacyjne, termiczne itp.).
wyraża jedną z głównych właściwości pola elektrostatycznego - jest nim potencjał (potencjalne są wszystkie pola, dla których zachodzi podobna zależność - grawitacyjne, termiczne itp.).
Graficzny obraz pola elektrostatycznego
mi 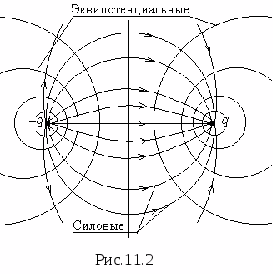 Pole elektrostatyczne wyznacza się, jeśli znane jest prawo zmiany natężenia i potencjału w funkcji współrzędnych. Można go wyraźniej scharakteryzować za pomocą układu sił i linii ekwipotencjalnych, co nazywa się jego obrazem graficznym. Linia sił to linia narysowana w polu w pamięci, która zaczyna się na ciele naładowanym dodatnio, a kończy na ciele naładowanym ujemnie, a styczna do której w dowolnym punkcie wyznacza kierunek wektora mi. Bardzo mały ładunek dodatni poruszałby się wzdłuż linii siły, mając zdolność swobodnego poruszania się i nie mając bezwładności. Ponieważ ładunki dodatnie i ujemne nie mogą znajdować się w tym samym punkcie, linie siły mają początek i koniec, nie mogą się one zamykać. W dowolnym polu elektrostatycznym powierzchnie ekwipotencjalne można narysować jako zbiory punktów o tym samym potencjale. Jeśli pole zostanie przecięte dowolną płaszczyzną, to w powstałym przekroju widoczne będą ślady powierzchni ekwipotencjalnych, które nazywane są liniami ekwipotencjalnymi. W przeciwieństwie do linii sił, linie ekwipotencjalne są ciągłe, zamknięte w sobie. W dowolnym punkcie pola linie siły i ekwipotencjału są do siebie prostopadłe. Jako przykład podajemy graficzny obraz pola elektrostatycznego dwóch ładunków punktowych (ryc. 11.2).
Pole elektrostatyczne wyznacza się, jeśli znane jest prawo zmiany natężenia i potencjału w funkcji współrzędnych. Można go wyraźniej scharakteryzować za pomocą układu sił i linii ekwipotencjalnych, co nazywa się jego obrazem graficznym. Linia sił to linia narysowana w polu w pamięci, która zaczyna się na ciele naładowanym dodatnio, a kończy na ciele naładowanym ujemnie, a styczna do której w dowolnym punkcie wyznacza kierunek wektora mi. Bardzo mały ładunek dodatni poruszałby się wzdłuż linii siły, mając zdolność swobodnego poruszania się i nie mając bezwładności. Ponieważ ładunki dodatnie i ujemne nie mogą znajdować się w tym samym punkcie, linie siły mają początek i koniec, nie mogą się one zamykać. W dowolnym polu elektrostatycznym powierzchnie ekwipotencjalne można narysować jako zbiory punktów o tym samym potencjale. Jeśli pole zostanie przecięte dowolną płaszczyzną, to w powstałym przekroju widoczne będą ślady powierzchni ekwipotencjalnych, które nazywane są liniami ekwipotencjalnymi. W przeciwieństwie do linii sił, linie ekwipotencjalne są ciągłe, zamknięte w sobie. W dowolnym punkcie pola linie siły i ekwipotencjału są do siebie prostopadłe. Jako przykład podajemy graficzny obraz pola elektrostatycznego dwóch ładunków punktowych (ryc. 11.2).
Czwiązek pomiędzy natężeniem pola a potencjałem
Wyjaśniona wcześniej zależność pomiędzy napięciem a potencjałem  nazywana całką. W praktyce częściej stosuje się zależność różnicową między tymi wielkościami; aby to wyjaśnić, zidentyfikujmy dwie linie ekwipotencjalne w pewnym polu elektrostatycznym (ryc. 11.3). Niech wszystkie punkty pierwszej linii mają potencjał φ
1, a drugi – φ
2. Dla pewności założymy to φ
1 >φ
2, ale różnią się one w nieskończenie małej ilości, tj. φ
1 -φ
2 =Dφ
. Odległość między liniami – dł. Wybierzmy dowolny punkt 1 na pierwszej linii i punkt 2 na drugiej, jeśli różnicę potencjałów między tymi punktami podzielimy przez najkrótszą odległość między nimi (w linii prostej).
nazywana całką. W praktyce częściej stosuje się zależność różnicową między tymi wielkościami; aby to wyjaśnić, zidentyfikujmy dwie linie ekwipotencjalne w pewnym polu elektrostatycznym (ryc. 11.3). Niech wszystkie punkty pierwszej linii mają potencjał φ
1, a drugi – φ
2. Dla pewności założymy to φ
1 >φ
2, ale różnią się one w nieskończenie małej ilości, tj. φ
1 -φ
2 =Dφ
. Odległość między liniami – dł. Wybierzmy dowolny punkt 1 na pierwszej linii i punkt 2 na drugiej, jeśli różnicę potencjałów między tymi punktami podzielimy przez najkrótszą odległość między nimi (w linii prostej).  uzyskana wartość będzie charakteryzowała szybkość zmiany potencjału w kierunku najkrótszej odległości między punktami. Prędkość ta zależy od sposobu wybierania punktów. Jeśli np. punkt 2 zostanie przesunięty w górę, to spadnie, bo tak nie jest Dφ
ulegnie zmianie, a odległość między punktami wzrośnie. Jeśli punkt 2 zostanie przesunięty w dół, wskazywana prędkość wzrasta. Kiedy punkt 2 zajmie pozycję najbliższą punktowi 1 (punkt 3), tempo potencjalnej zmiany osiągnie maksimum. W matematyce pojęcie gradientu funkcji skalarnej wprowadza się jako szybkość jej zmian, przyjmowaną w kierunku największego wzrostu. Zastosujmy to pojęcie do potencjału, tj. rozważać absolwentφ
. Będzie to wektor - ma kierunek od punktu 3 do punktu 1 (kierunek największego wzrostu), a jego moduł jest równy
uzyskana wartość będzie charakteryzowała szybkość zmiany potencjału w kierunku najkrótszej odległości między punktami. Prędkość ta zależy od sposobu wybierania punktów. Jeśli np. punkt 2 zostanie przesunięty w górę, to spadnie, bo tak nie jest Dφ
ulegnie zmianie, a odległość między punktami wzrośnie. Jeśli punkt 2 zostanie przesunięty w dół, wskazywana prędkość wzrasta. Kiedy punkt 2 zajmie pozycję najbliższą punktowi 1 (punkt 3), tempo potencjalnej zmiany osiągnie maksimum. W matematyce pojęcie gradientu funkcji skalarnej wprowadza się jako szybkość jej zmian, przyjmowaną w kierunku największego wzrostu. Zastosujmy to pojęcie do potencjału, tj. rozważać absolwentφ
. Będzie to wektor - ma kierunek od punktu 3 do punktu 1 (kierunek największego wzrostu), a jego moduł jest równy 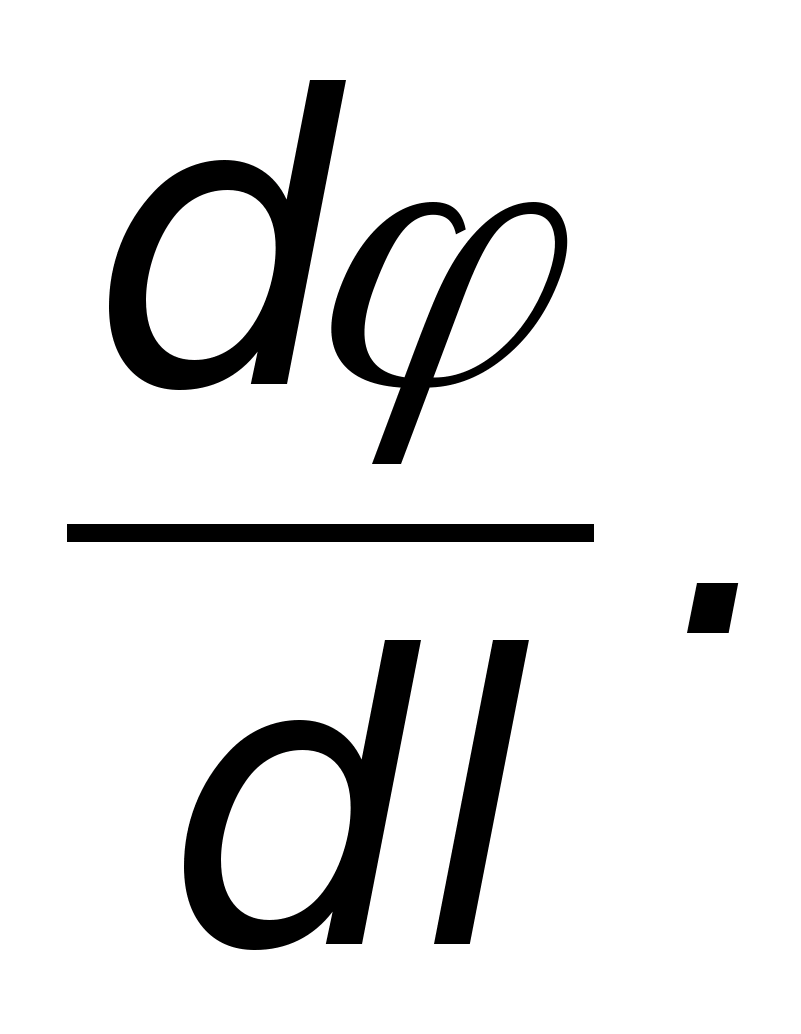 Siła pola jest skierowana
z wyższego potencjału ( φ
1) do mniejszego ( φ
2), a jego moduł jest równy
Siła pola jest skierowana
z wyższego potencjału ( φ
1) do mniejszego ( φ
2), a jego moduł jest równy 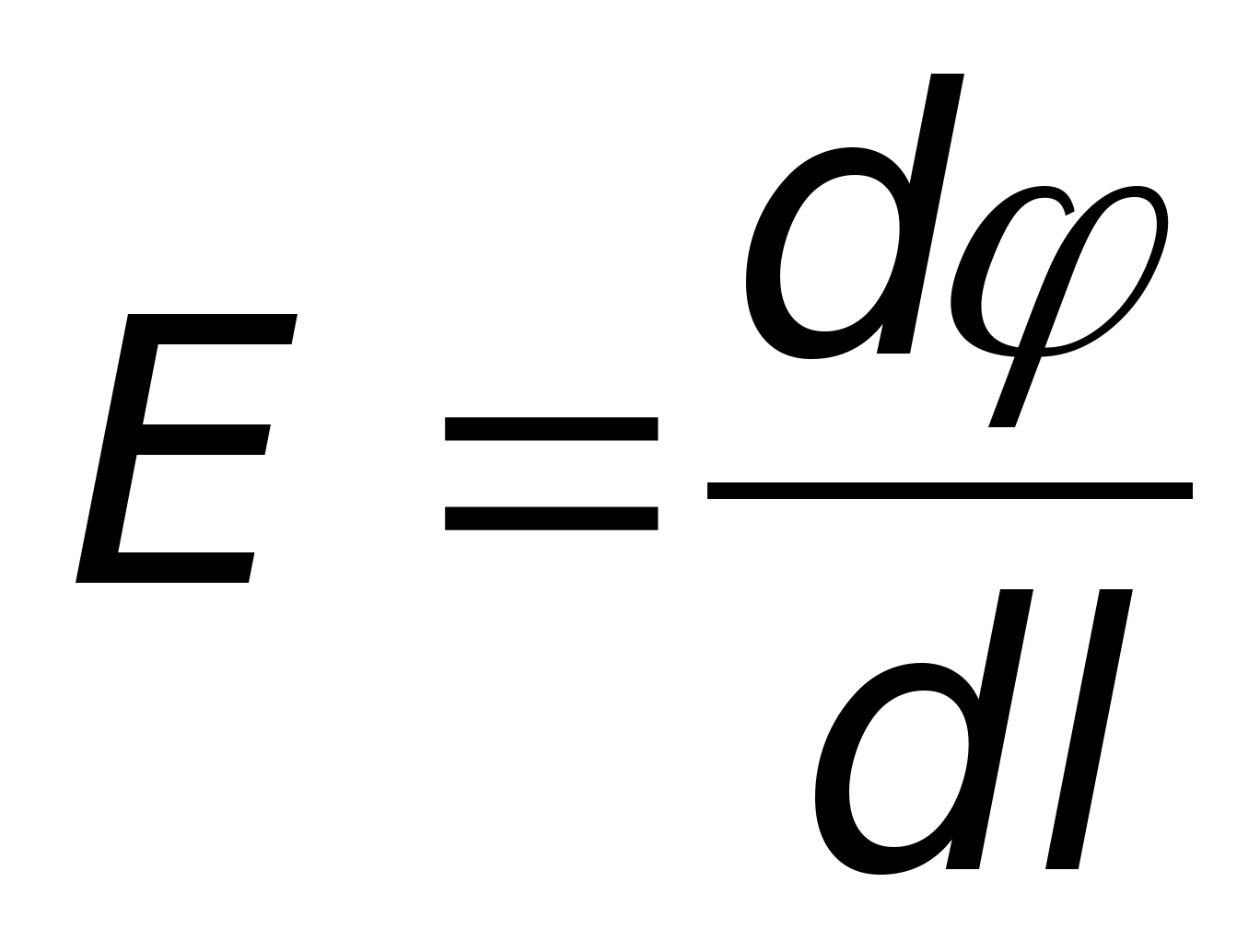 (patrz formularz integralny). Ponieważ moduły wektorów mi i gradφ są takie same, ale są zatem skierowane w przeciwne strony
(patrz formularz integralny). Ponieważ moduły wektorów mi i gradφ są takie same, ale są zatem skierowane w przeciwne strony 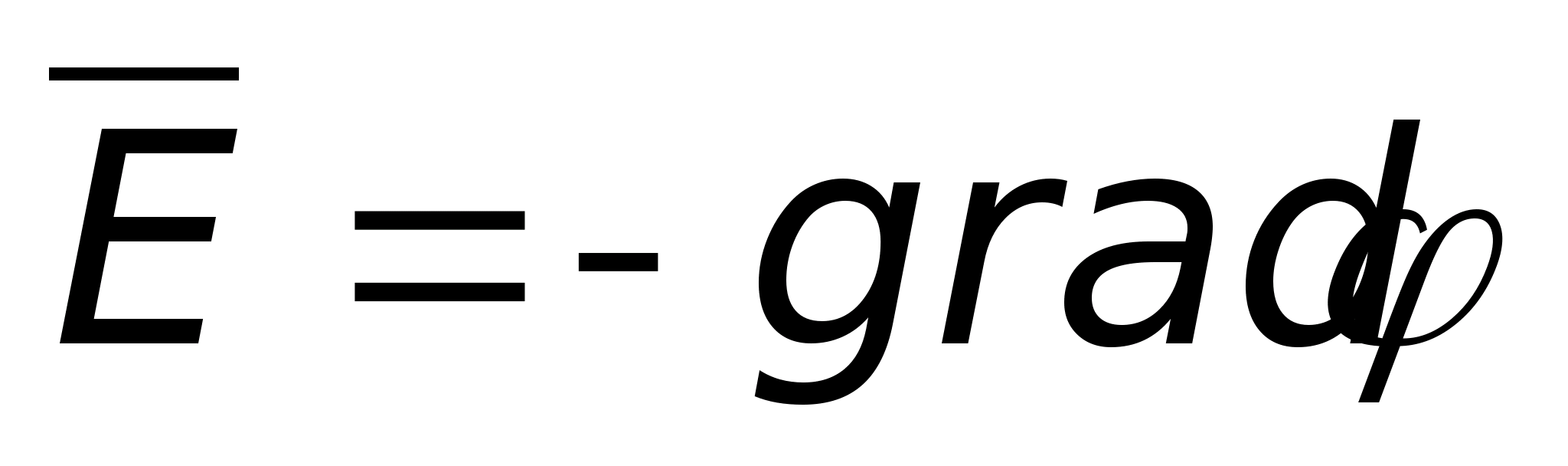 .
.
Kierunek największego wzrostu potencjału w ogólnym przypadku nie pokrywa się zatem z żadną osią współrzędnych absolwentφ
jest przedstawiany jako suma rzutów wzdłuż osi współrzędnych, na przykład w prostokątnym układzie współrzędnych (ryc. 11.4) 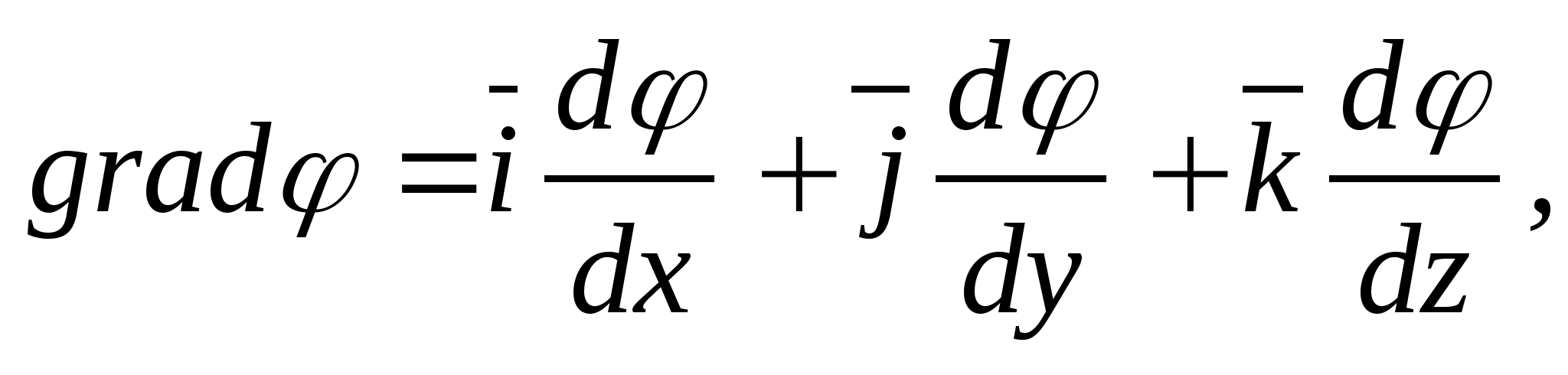 Gdzie
Gdzie  - wektory (wektory jednostkowe) układu prostokątnego,
- wektory (wektory jednostkowe) układu prostokątnego, 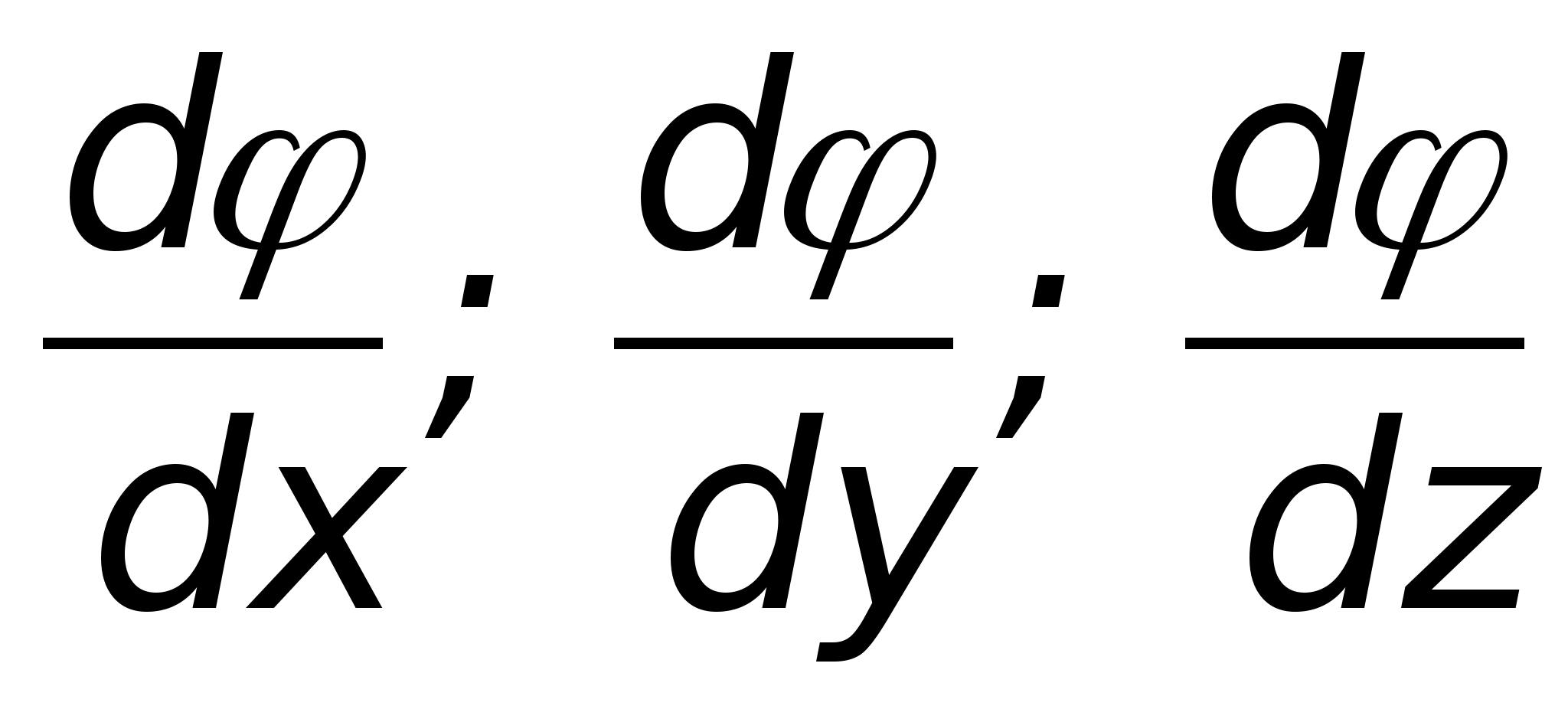 - szybkość zmian potencjału wzdłuż odpowiedniej osi. Napięcie mi można również zapisać za pomocą projekcji
- szybkość zmian potencjału wzdłuż odpowiedniej osi. Napięcie mi można również zapisać za pomocą projekcji  Dwa wektory są sobie równe, jeśli mają te same rzuty, tj.
Dwa wektory są sobie równe, jeśli mają te same rzuty, tj. 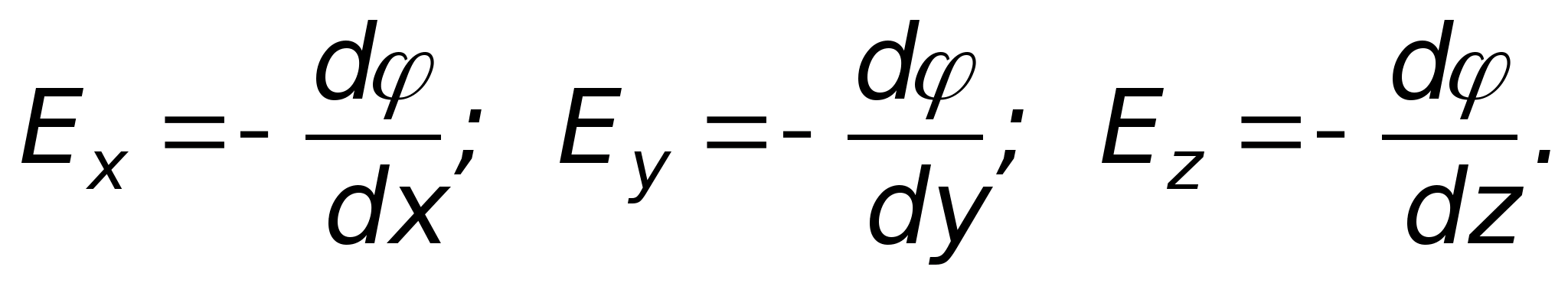 W obliczeniach praktycznych wykorzystywane są trzy ostatnie wzory.
W obliczeniach praktycznych wykorzystywane są trzy ostatnie wzory.
Aby skrócić zapis różnych operacji w teorii pola, powszechnie stosuje się operator różniczkowy Hamiltona (nabla), który nie ma fizycznego znaczenia, rozumiany jako suma pochodnych cząstkowych wzdłuż osi współrzędnych pomnożona przez odpowiednie wektory jednostkowe. W kartezjańskim układzie współrzędnych ma on postać: 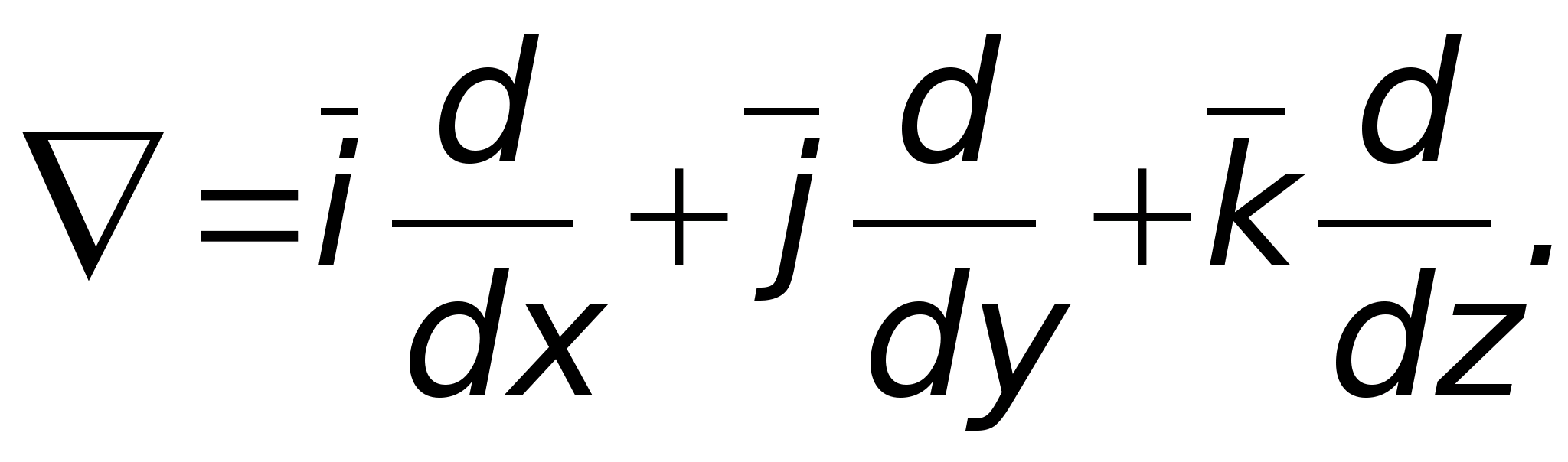 Formalnie nabla można uznać za wektor. Można go zastosować zarówno do funkcji skalarnych, jak i wektorowych. Funkcja, na podstawie której wykonywana jest akcja (różniczkowanie wzdłuż osi współrzędnych lub różniczkowanie przestrzenne), jest zapisywana po prawej stronie
Formalnie nabla można uznać za wektor. Można go zastosować zarówno do funkcji skalarnych, jak i wektorowych. Funkcja, na podstawie której wykonywana jest akcja (różniczkowanie wzdłuż osi współrzędnych lub różniczkowanie przestrzenne), jest zapisywana po prawej stronie  Jeśli po prawej stronie
Jeśli po prawej stronie  Jeśli funkcja nie jest określona, wówczas sam operator nabla nie jest używany (podobnie jak sin, log itp.). Zastosowanie operatora nabla do potencjału
Jeśli funkcja nie jest określona, wówczas sam operator nabla nie jest używany (podobnie jak sin, log itp.). Zastosowanie operatora nabla do potencjału  i porównując to z
i porównując to z  , widzimy, że =
, widzimy, że =  (dla funkcji skalarnej pochodne cząstkowe i całkowite są takie same). Wówczas związek pomiędzy napięciem a potencjałem można zapisać następująco:
(dla funkcji skalarnej pochodne cząstkowe i całkowite są takie same). Wówczas związek pomiędzy napięciem a potencjałem można zapisać następująco: 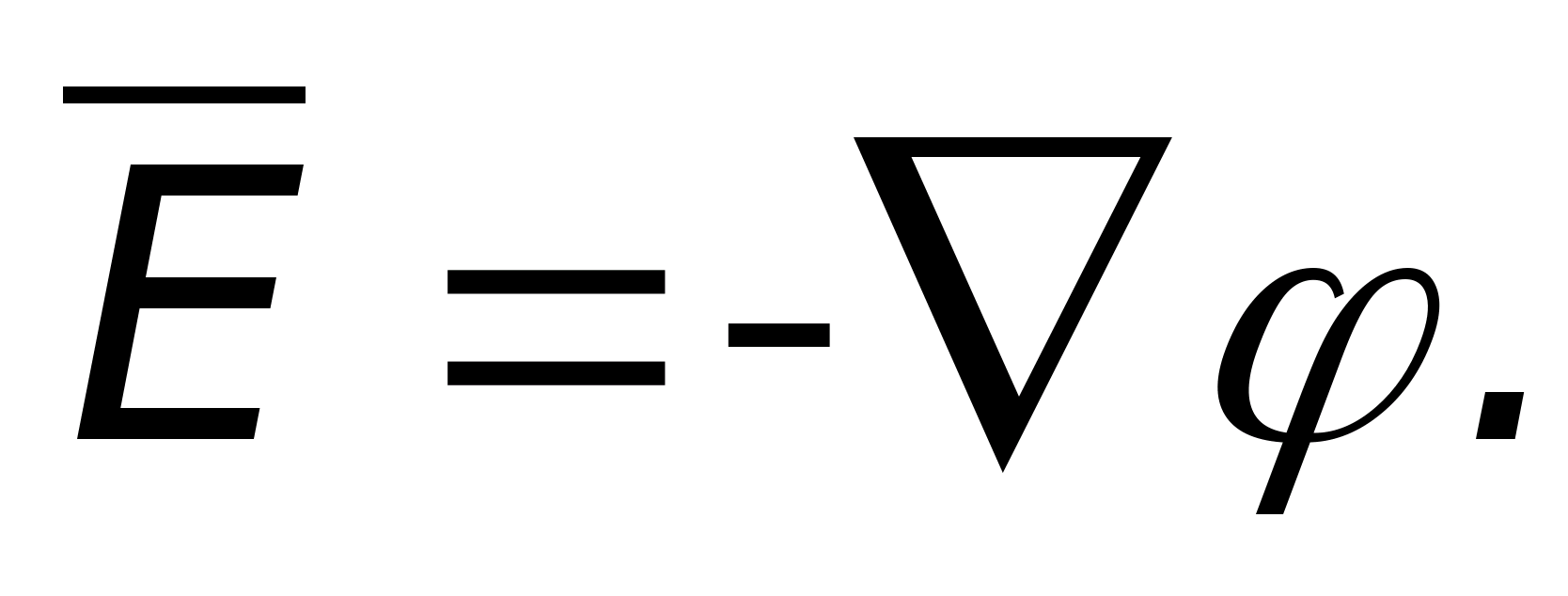
Polaryzacja materii
W substancjach rozróżnia się ładunki wolne i związane. Ładunki swobodne to takie, które pod wpływem sił pola mogą swobodnie poruszać się w substancji; ich ruch nie jest ograniczony siłami wewnątrzcząsteczkowymi. Przez związane ładunki rozumiemy te, które pod wpływem sił pola mogą poruszać się jedynie wewnątrz cząsteczki. Ładunki związane są nierozerwalnie związane z materią, dlatego suma ładunków dodatnich jest równa sumie ładunków ujemnych.
D 
Ciała elektryczne w polu elektrostatycznym są spolaryzowane. Przez polaryzację rozumie się uporządkowaną zmianę rozmieszczenia związanych ładunków pod wpływem sił pola. Polaryzację można wyraźnie pokazać korzystając z ryc. 11.5, który przedstawia ciało przy braku pola elektrostatycznego i w jego obecności. Jeśli nie ma pola, wówczas cząsteczki (dipole) znajdują się w nieładzie chaotycznym (ryc. 11.5, a). W ciele spolaryzowanym ładunki związane dodatnio przesuwają się w stronę wyższego potencjału, a ujemne w stronę niższego potencjału (ryc. 11.5, b) i przesuwają się tak bardzo, że siły pola elektrycznego równoważą siły wewnątrzcząsteczkowe. W wyniku polaryzacji na powierzchni substancji pojawiają się dodatnie lub ujemne ładunki związane, a suma pierwszego z nich jest dokładnie równa sumie drugiego. Dipole tworzą własne pola. W substancji niespolaryzowanej ich całkowity efekt wynosi zero, ale w substancji spolaryzowanej tak nie jest; prowadzi to do osłabienia powstałego pola i należy to wziąć pod uwagę. W tym celu wprowadzono pojęcie momentu elektrycznego dipola. Moment elektryczny dwóch ładunków o jednakowej wielkości i przeciwnych znakach, znajdujących się w pewnej odległości od siebie l, praca nazywa się 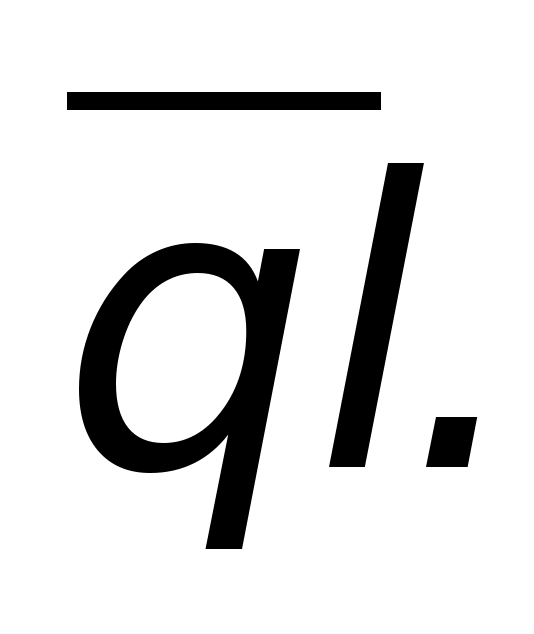 To jest wektor skierowany z - Q k + Q(ryc. 11.6). Pod wpływem pola zewnętrznego dipole substancji mają tendencję do orientowania się w taki sposób, że ich momenty elektryczne pokrywają się z natężeniem pola zewnętrznego. Praktyczne znaczenie ma oczywiście nie tylko jeden dipol i jego moment elektryczny (jest niezwykle mały), ale suma momentów elektrycznych dipoli znajdujących się w jednostkowej objętości, co zwykle nazywa się wektorem polaryzacji
To jest wektor skierowany z - Q k + Q(ryc. 11.6). Pod wpływem pola zewnętrznego dipole substancji mają tendencję do orientowania się w taki sposób, że ich momenty elektryczne pokrywają się z natężeniem pola zewnętrznego. Praktyczne znaczenie ma oczywiście nie tylko jeden dipol i jego moment elektryczny (jest niezwykle mały), ale suma momentów elektrycznych dipoli znajdujących się w jednostkowej objętości, co zwykle nazywa się wektorem polaryzacji 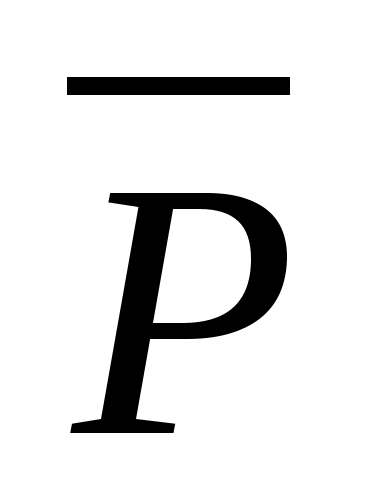 , tj.
, tj.  W przypadku większości dielektryków wektor polaryzacji jest proporcjonalny do natężenia pola
W przypadku większości dielektryków wektor polaryzacji jest proporcjonalny do natężenia pola  oraz współczynnik proporcjonalności pomiędzy nimi k nazywana podatnością elektryczną.
oraz współczynnik proporcjonalności pomiędzy nimi k nazywana podatnością elektryczną.
Oprócz wielkości wektorowych omówionych powyżej 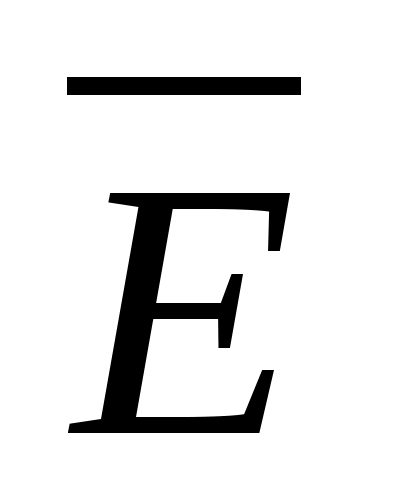 i , którego fizyczne znaczenie wyjaśniliśmy, w teorii pola do obliczeń wprowadza się inny wektor
i , którego fizyczne znaczenie wyjaśniliśmy, w teorii pola do obliczeń wprowadza się inny wektor  , który nazywany jest wektorem przemieszczenia elektrycznego lub wektorem indukcji elektrycznej. Definiuje się to następująco: gdzie
, który nazywany jest wektorem przemieszczenia elektrycznego lub wektorem indukcji elektrycznej. Definiuje się to następująco: gdzie 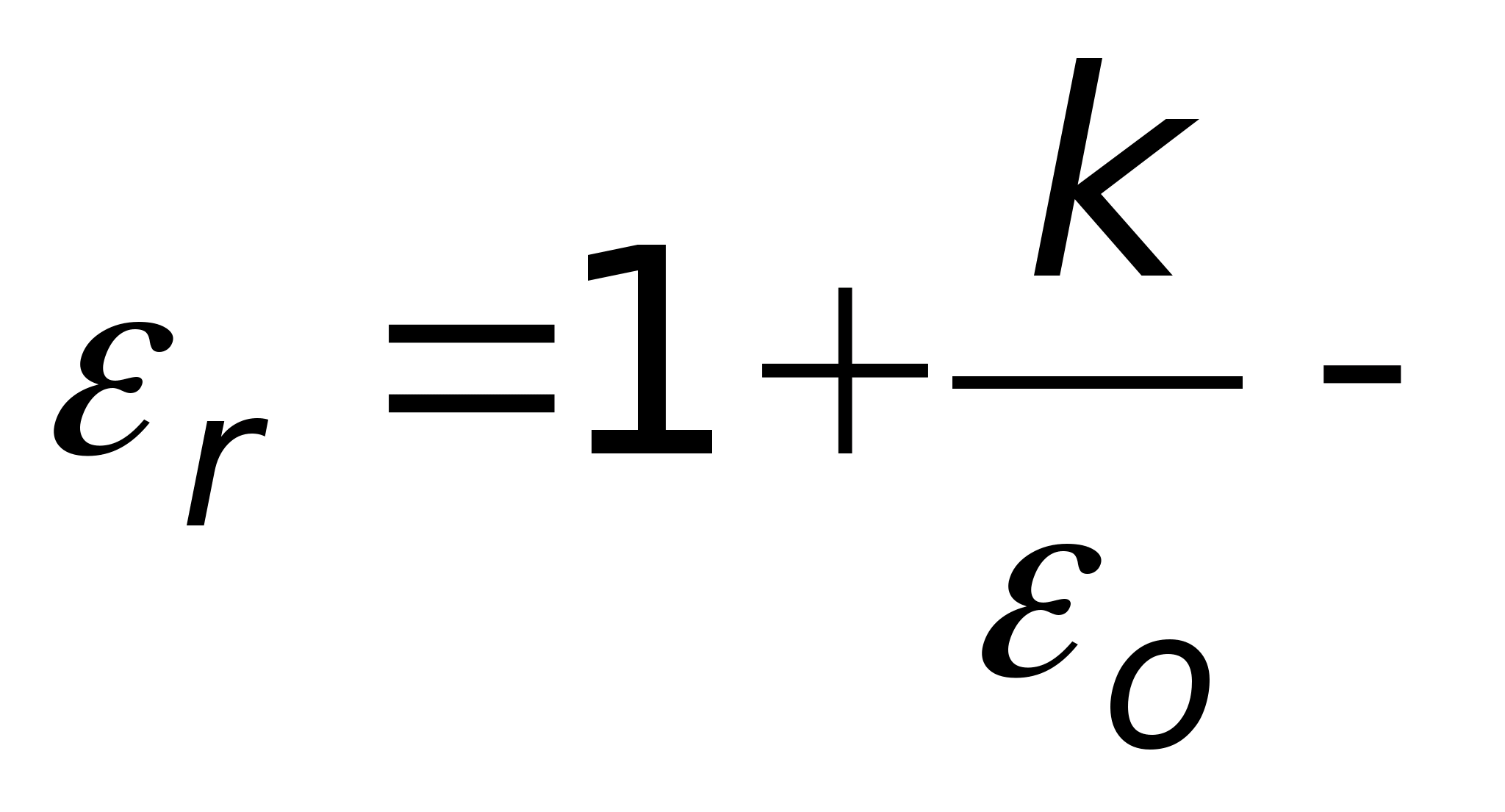 nazywa się względną stałą dielektryczną ośrodka, w którym pole jest utworzone, oraz
nazywa się względną stałą dielektryczną ośrodka, w którym pole jest utworzone, oraz  bezwzględna stała dielektryczna ośrodka, w którym pole jest wytworzone.
bezwzględna stała dielektryczna ośrodka, w którym pole jest wytworzone. 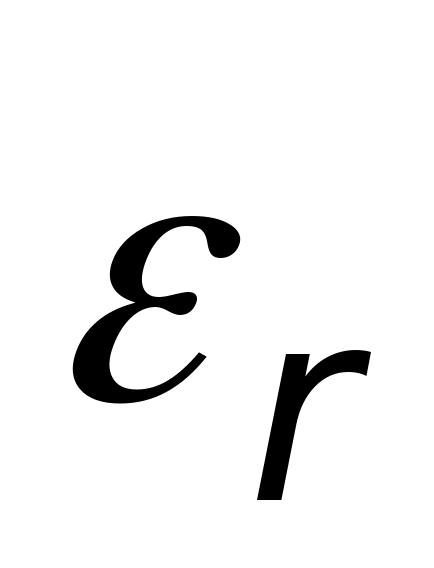 pokazuje, ile razy właściwości elektryczne ośrodka różnią się od właściwości próżni (różnica ta wynika z polaryzacji). Dla wszystkich środowisk jest ona ustalana eksperymentalnie i podana w podręcznikach.
pokazuje, ile razy właściwości elektryczne ośrodka różnią się od właściwości próżni (różnica ta wynika z polaryzacji). Dla wszystkich środowisk jest ona ustalana eksperymentalnie i podana w podręcznikach.
Twierdzenie Gaussa
Twierdzenie Gaussa jest podstawowym prawem pola elektrostatycznego. Zostało to odkryte eksperymentalnie i zapisane matematycznie w następujący sposób 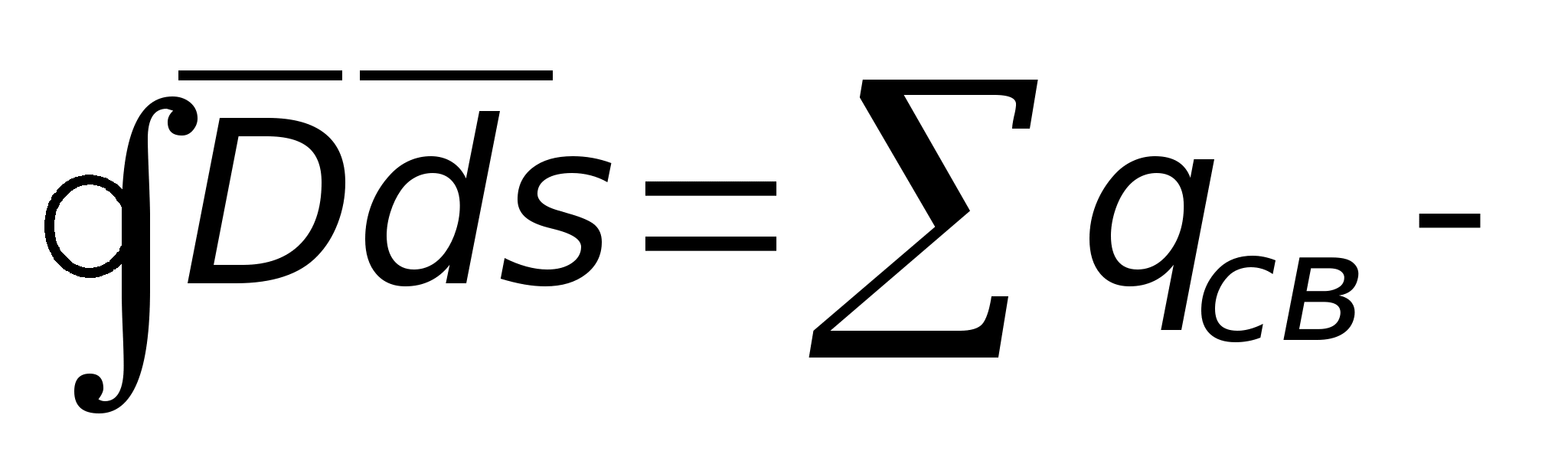 przepływ wektora przemieszczenia elektrycznego przez dowolną zamkniętą powierzchnię otaczającą pewną objętość jest równy sumie algebraicznej wolnych ładunków znajdujących się wewnątrz tej powierzchni (w sumie
przepływ wektora przemieszczenia elektrycznego przez dowolną zamkniętą powierzchnię otaczającą pewną objętość jest równy sumie algebraicznej wolnych ładunków znajdujących się wewnątrz tej powierzchni (w sumie 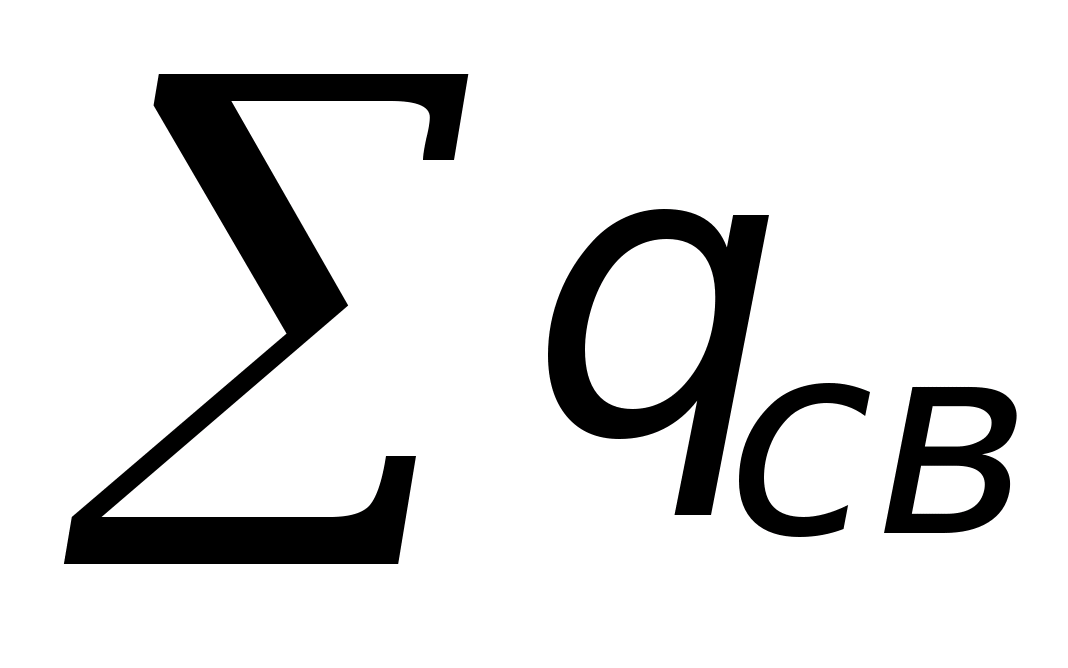 opłaty pobierane są wraz z ich znakami). Od
opłaty pobierane są wraz z ich znakami). Od  To
To  .
.  Do mediów jednorodnych i izotropowych
Do mediów jednorodnych i izotropowych 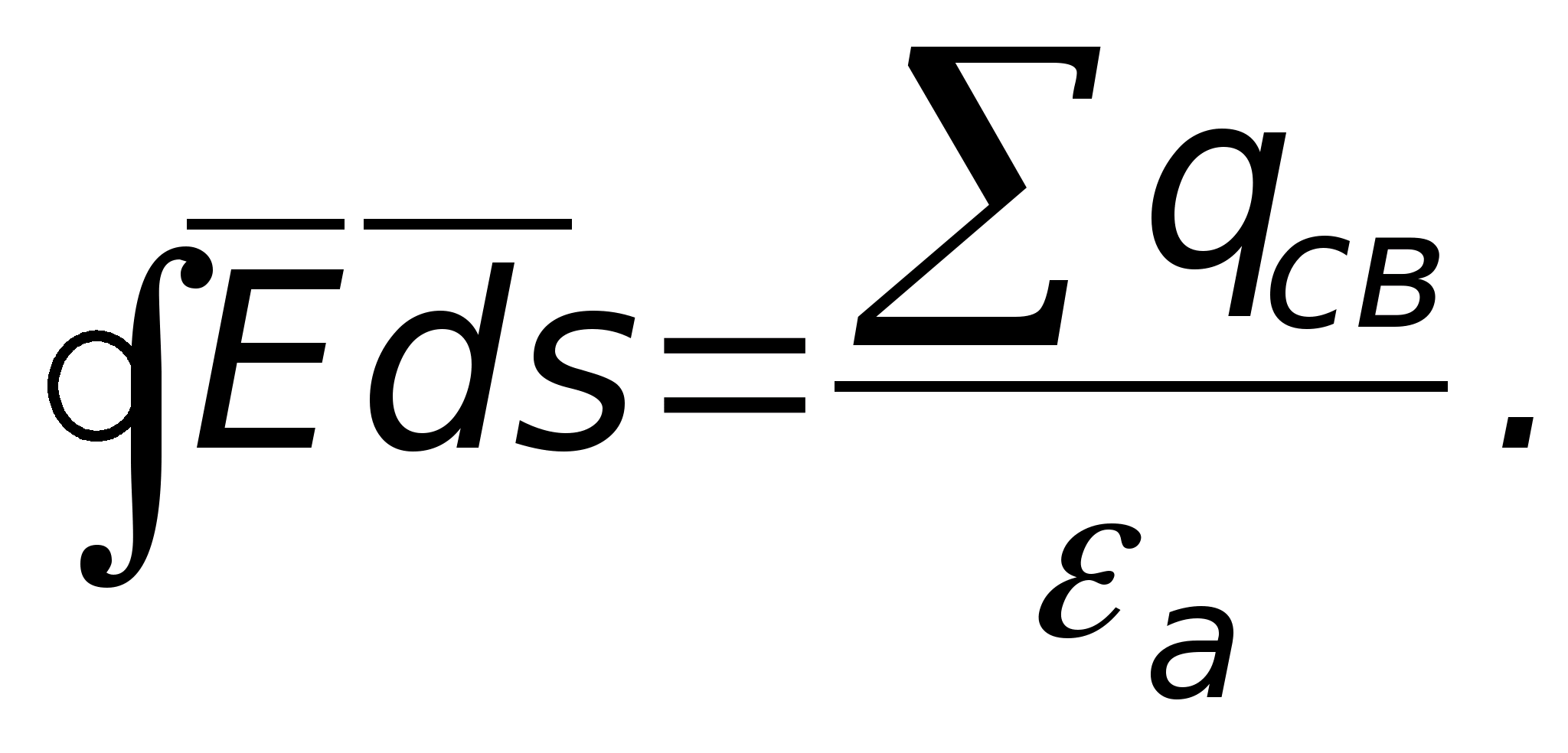 jest wartością stałą i można ją wówczas wyjąć ze znaku całki Co ciekawe, przepływ wektorowy D mi Lub mi zależy tylko i nie zależy od rozmieszczenia ładunków wewnątrz zamkniętej powierzchni. Wektor przepływu
jest wartością stałą i można ją wówczas wyjąć ze znaku całki Co ciekawe, przepływ wektorowy D mi Lub mi zależy tylko i nie zależy od rozmieszczenia ładunków wewnątrz zamkniętej powierzchni. Wektor przepływu 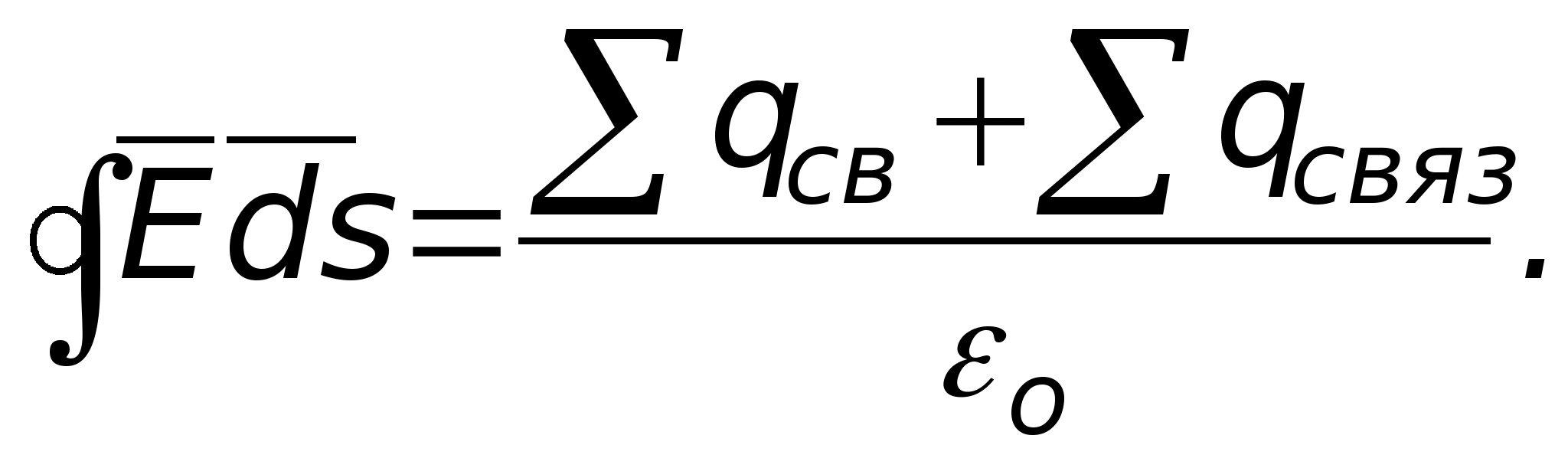 tworzone są nie tylko przez opłaty bezpłatne, ale także przez opłaty powiązane. Te ostatnie można uwzględnić nie poprzez , ale poprzez osobną sumę związanych ładunków i wtedy wzór na twierdzenie Gaussa wygląda następująco:
tworzone są nie tylko przez opłaty bezpłatne, ale także przez opłaty powiązane. Te ostatnie można uwzględnić nie poprzez , ale poprzez osobną sumę związanych ładunków i wtedy wzór na twierdzenie Gaussa wygląda następująco:
Te trzy wzory stanowią integralną formę twierdzenia Gaussa, które można zastosować z dużą wydajnością i prostotą do obliczenia natężenia pola w dowolnym punkcie, jeśli można przez niego przeciągnąć zamkniętą powierzchnię, której wszystkie punkty znajdują się w tych samych warunkach pod względem do ładunków, tworząc pole. Jako przykład obliczmy pole utworzone przez ładunek punktowy.  T
T 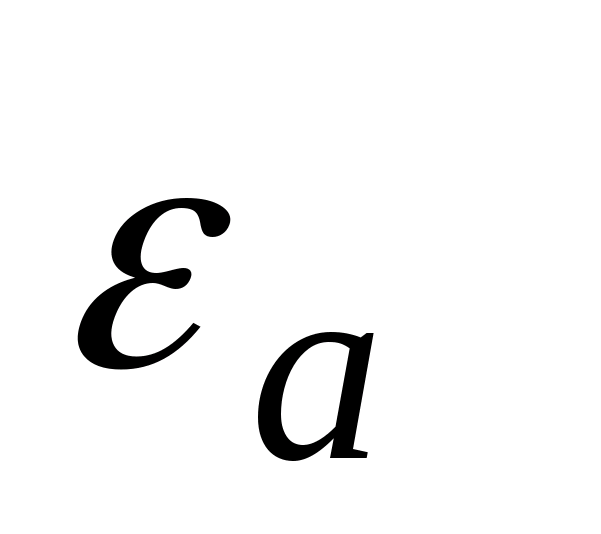 Ładunek punktowy to ładunek umieszczony na ciele o bardzo małych wymiarach geometrycznych. Na ryc. 11.7 będzie on przedstawiony jako punkt (stąd nazwa). Załóżmy, że ładunek ten jest dodatni i znajduje się w ośrodku przepuszczalnym . Weźmy dowolny punkt oddzielony odległością
Ładunek punktowy to ładunek umieszczony na ciele o bardzo małych wymiarach geometrycznych. Na ryc. 11.7 będzie on przedstawiony jako punkt (stąd nazwa). Załóżmy, że ładunek ten jest dodatni i znajduje się w ośrodku przepuszczalnym . Weźmy dowolny punkt oddzielony odległością  R mi z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory pokrywają się, wówczas ich produkt pokrywa się z produktem modułów. Ponadto we wszystkich punktach rozważanej kuli wielkość wektora mi to samo ze względu na symetrię. Biorąc to pod uwagę, mamy: ponieważ powierzchnia kuli jest równa
R mi z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory pokrywają się, wówczas ich produkt pokrywa się z produktem modułów. Ponadto we wszystkich punktach rozważanej kuli wielkość wektora mi to samo ze względu na symetrię. Biorąc to pod uwagę, mamy: ponieważ powierzchnia kuli jest równa 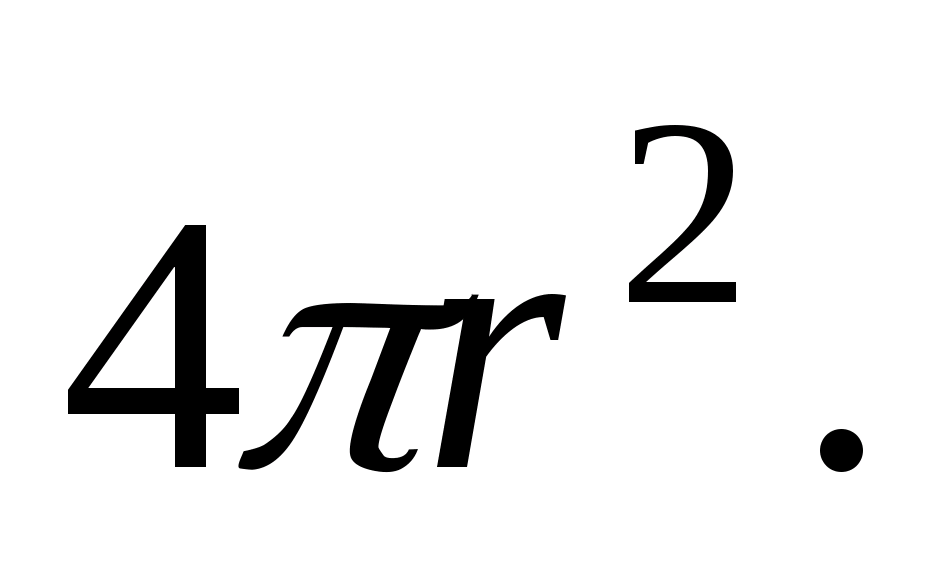 Suma opłat bezpłatnych jest równa tylko danej opłacie punktowej
Suma opłat bezpłatnych jest równa tylko danej opłacie punktowej 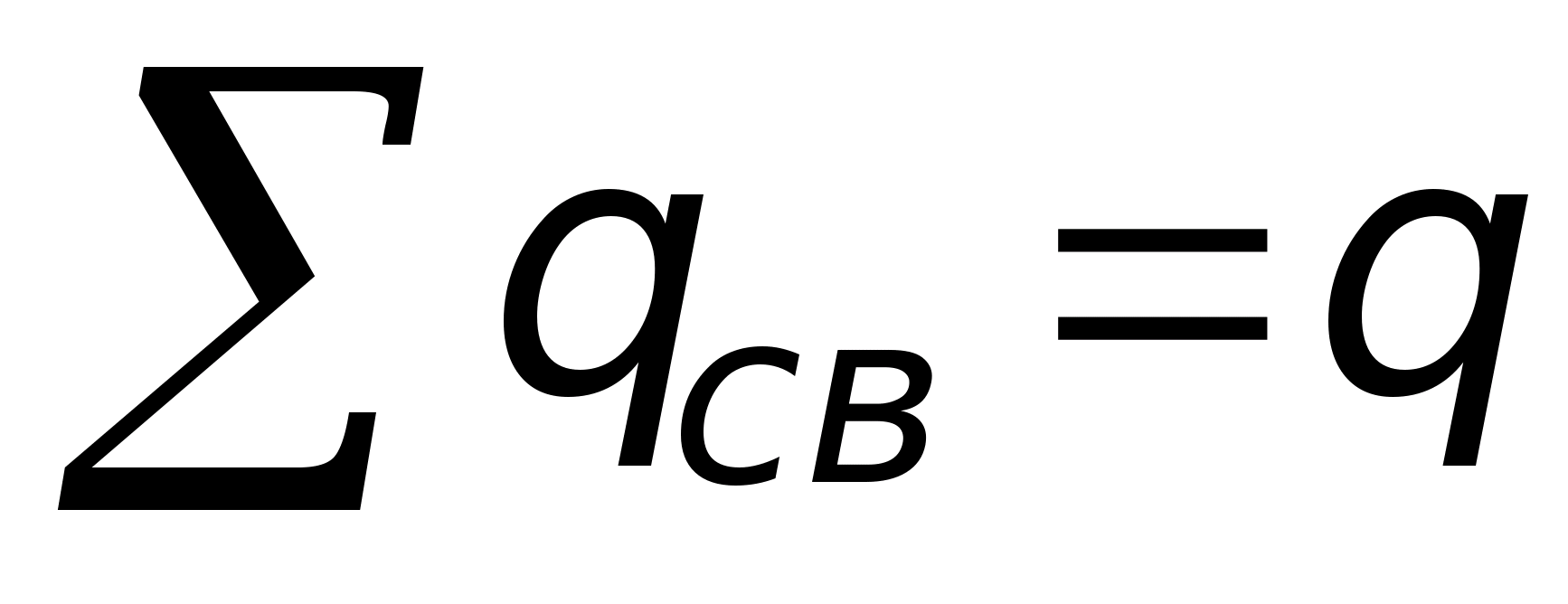 . Podstawiając te wartości do wzoru twierdzenia Gaussa, otrzymujemy:
. Podstawiając te wartości do wzoru twierdzenia Gaussa, otrzymujemy:  Zatem w danym polu natężenie zmienia się odwrotnie proporcjonalnie do . 2 .
Zatem w danym polu natężenie zmienia się odwrotnie proporcjonalnie do . 2 .
Obliczmy potencjał w tym polu na podstawie wzoru. Jeśli weźmiemy pod uwagę, że napięcie, a zatem i potencjał, zależą tylko od promienia, wówczas ostatni wzór zostanie przepisany w następujący sposób 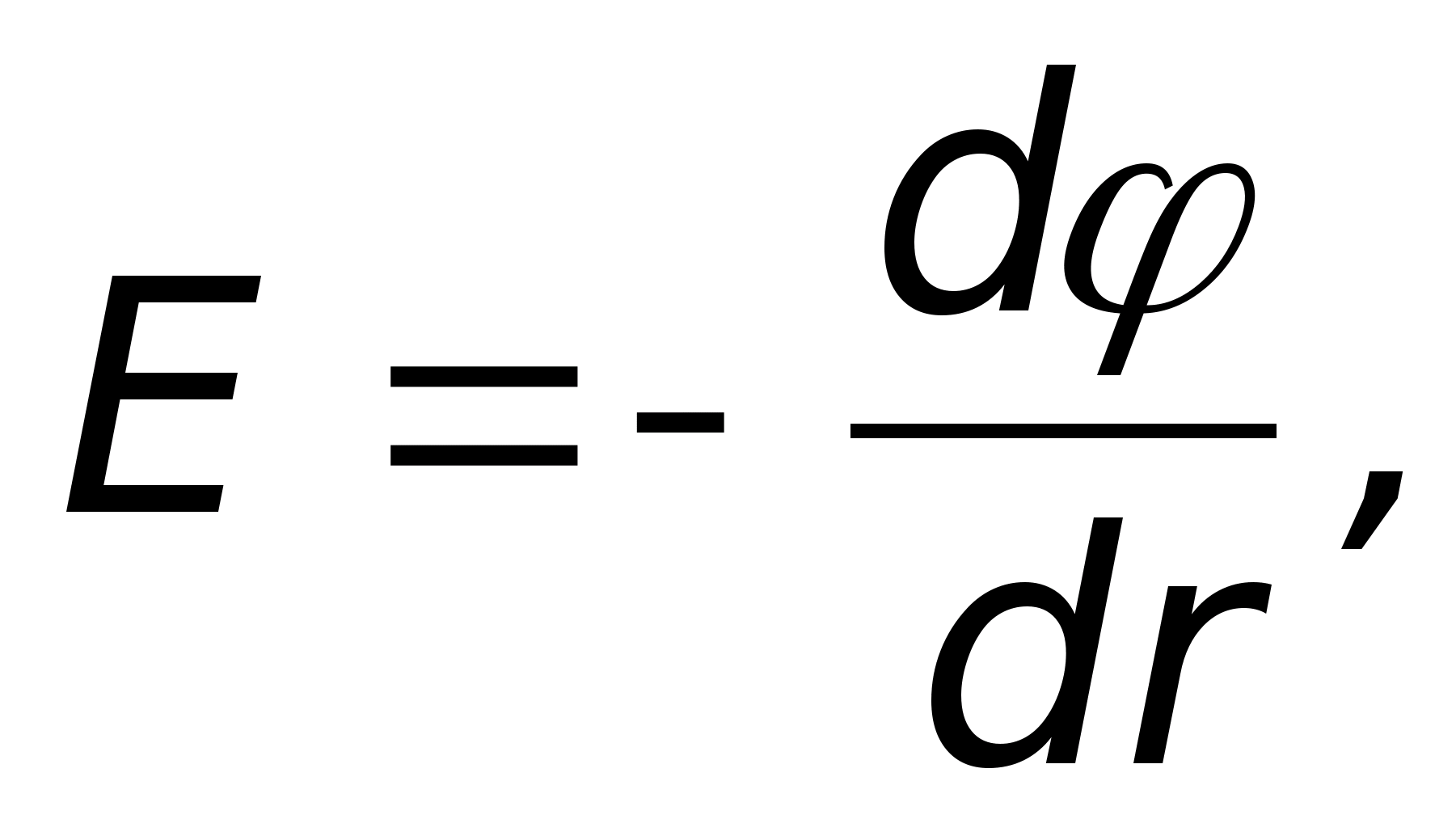 Gdzie
Gdzie 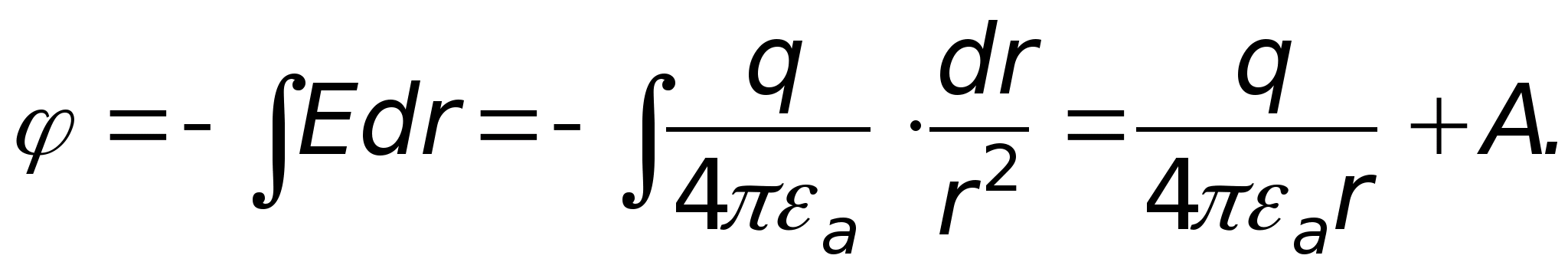 Wynika z tego, że potencjał w danym polu zmienia się odwrotnie proporcjonalnie do .. Stała całkowania A zależy od tego, gdzie znajduje się punkt o potencjale zerowym.
Wynika z tego, że potencjał w danym polu zmienia się odwrotnie proporcjonalnie do .. Stała całkowania A zależy od tego, gdzie znajduje się punkt o potencjale zerowym.
Całkowa postać zapisu twierdzenia Gaussa nie daje odpowiedzi na pytanie, jak natężenie pola w danym punkcie jest powiązane z ładunkiem w tym samym punkcie. Odpowiedź na to pytanie daje różniczkowa postać tego twierdzenia, która wynika z postaci całkowej. Do tego wyrażenie 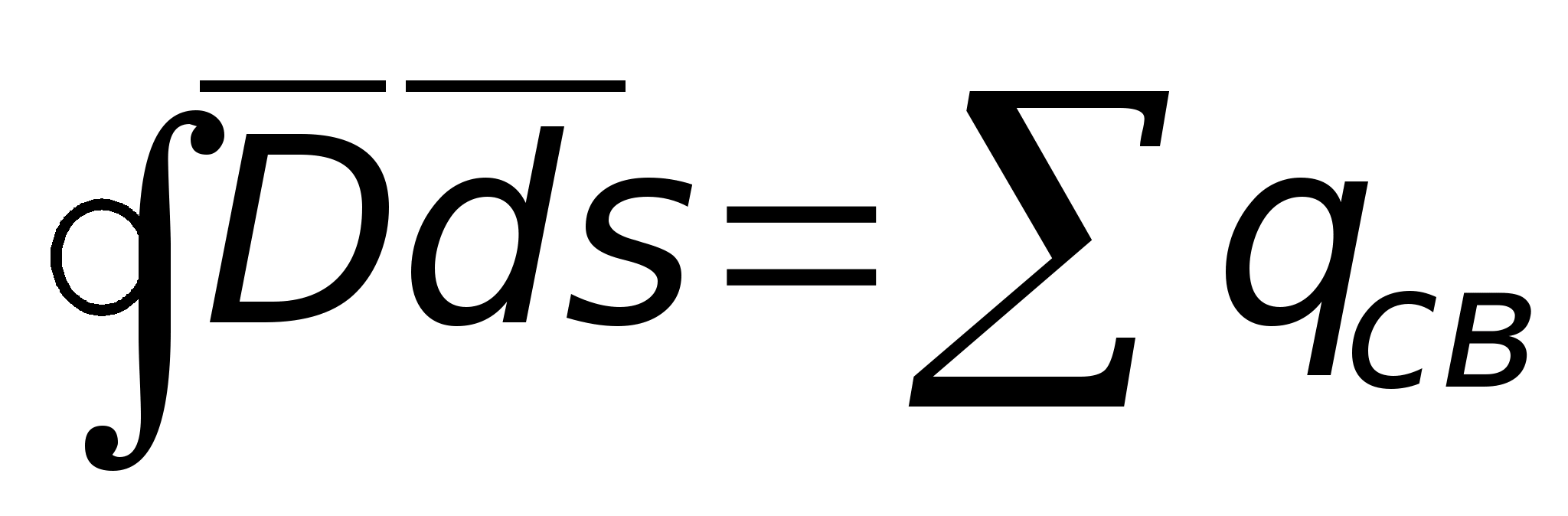 podzielić przez objętość ograniczoną powierzchnią całkowania
podzielić przez objętość ograniczoną powierzchnią całkowania 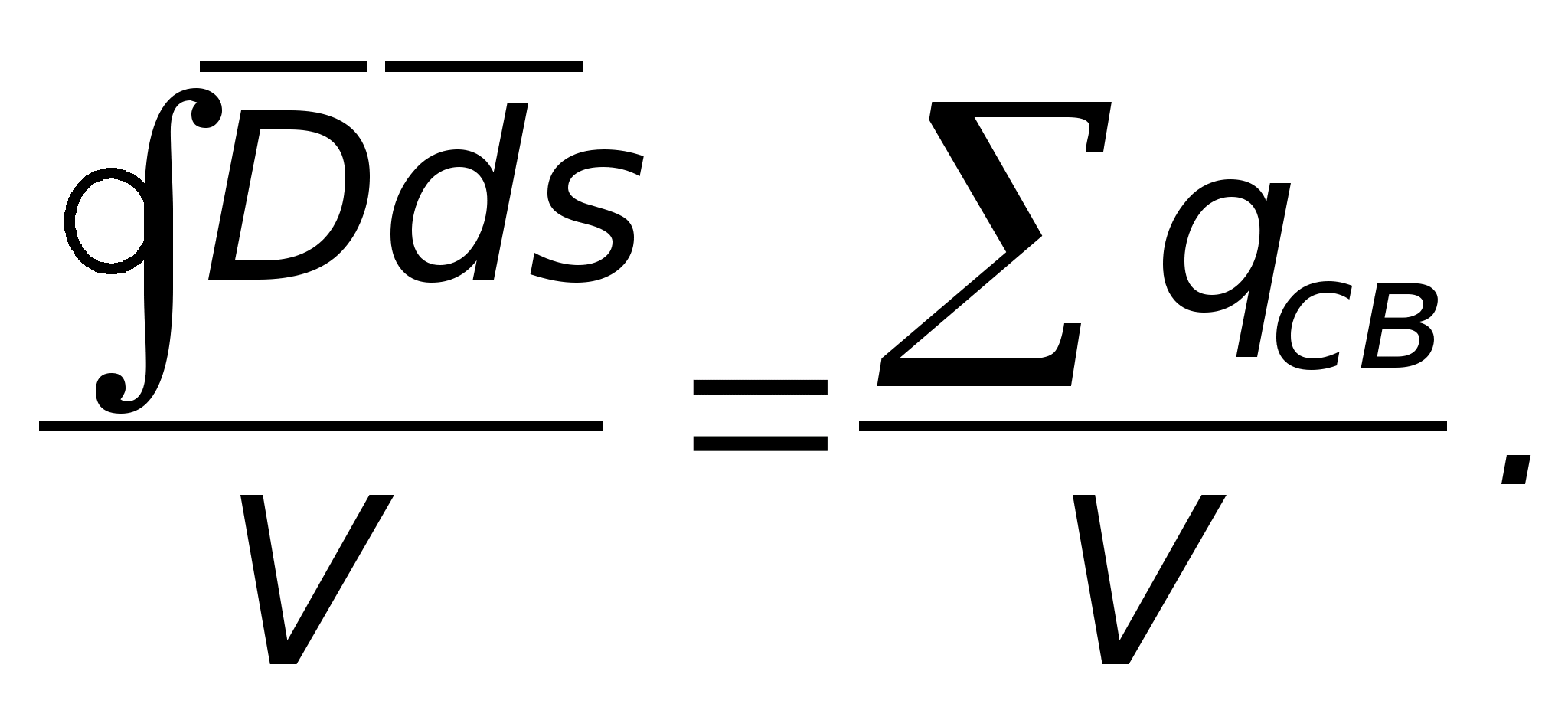 Zależność ta obowiązuje dla objętości o dowolnym rozmiarze. Skierujmy to na zero (mówią, że zmniejszymy powierzchnię do punktu). Następnie
Zależność ta obowiązuje dla objętości o dowolnym rozmiarze. Skierujmy to na zero (mówią, że zmniejszymy powierzchnię do punktu). Następnie  Limit współczynnika strumienia wektorowego Co ciekawe, przepływ wektorowy przez zamkniętą powierzchnię ograniczającą pewną objętość do wartości tej objętości nazywa się rozbieżnością wektora Co ciekawe, przepływ wektorowy
(
Limit współczynnika strumienia wektorowego Co ciekawe, przepływ wektorowy przez zamkniętą powierzchnię ograniczającą pewną objętość do wartości tej objętości nazywa się rozbieżnością wektora Co ciekawe, przepływ wektorowy
(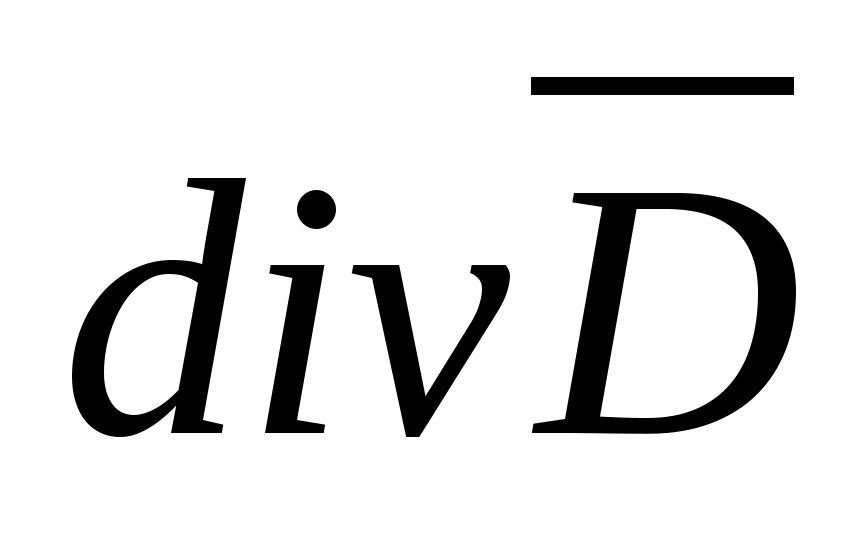 ) albo źródło, albo rozbieżność. Po prawej stronie ostatniej równości jest gęstość nasypowa bezpłatna opłata ρ
Św.. Następnie
) albo źródło, albo rozbieżność. Po prawej stronie ostatniej równości jest gęstość nasypowa bezpłatna opłata ρ
Św.. Następnie  To jest twierdzenie Gaussa w postaci różniczkowej. Wyjaśnijmy jego istotę za pomocą trzech przypadków, o
To jest twierdzenie Gaussa w postaci różniczkowej. Wyjaśnijmy jego istotę za pomocą trzech przypadków, o ![]() pokazano na ryc. 11.8. Jeżeli w rozważanym punkcie pola gęstość objętościowa ładunku swobodnego jest dodatnia, to z nieskończenie małej objętości otaczającej ten punkt linie wektora Co ciekawe, przepływ wektorowy pochodzą (źródło jest dodatnie, rozbieżność jest dodatnia, rozbieżność jest dodatnia). Jeżeli w rozważanym punkcie pola gęstość objętościowa ładunku swobodnego jest ujemna, to w nieskończenie małej objętości otaczającej ten punkt linie wektora Co ciekawe, przepływ wektorowy uwzględnione (źródło ujemne, rozbieżność ujemna, rozbieżność ujemna). I wreszcie, jeśli w rozważanym punkcie nie ma darmowego ładunku, to w takim punkcie nie ma ani drenażu, ani źródła linii wektorowych Co ciekawe, przepływ wektorowy, tj. w takim punkcie linii wektora Co ciekawe, przepływ wektorowy nie zaczynaj i nie kończ, ale przenikaj nieskończenie małą objętość otaczającą dany punkt.
pokazano na ryc. 11.8. Jeżeli w rozważanym punkcie pola gęstość objętościowa ładunku swobodnego jest dodatnia, to z nieskończenie małej objętości otaczającej ten punkt linie wektora Co ciekawe, przepływ wektorowy pochodzą (źródło jest dodatnie, rozbieżność jest dodatnia, rozbieżność jest dodatnia). Jeżeli w rozważanym punkcie pola gęstość objętościowa ładunku swobodnego jest ujemna, to w nieskończenie małej objętości otaczającej ten punkt linie wektora Co ciekawe, przepływ wektorowy uwzględnione (źródło ujemne, rozbieżność ujemna, rozbieżność ujemna). I wreszcie, jeśli w rozważanym punkcie nie ma darmowego ładunku, to w takim punkcie nie ma ani drenażu, ani źródła linii wektorowych Co ciekawe, przepływ wektorowy, tj. w takim punkcie linii wektora Co ciekawe, przepływ wektorowy nie zaczynaj i nie kończ, ale przenikaj nieskończenie małą objętość otaczającą dany punkt.
Od  To
To  Do mediów jednorodnych i izotropowych
Do mediów jednorodnych i izotropowych  jest wartością stałą i można ją usunąć ze znaku dz, wówczas otrzymujemy:
jest wartością stałą i można ją usunąć ze znaku dz, wówczas otrzymujemy:  Jeśli uwzględni się zjawisko polaryzacji przy użyciu związanych ładunków, to ostatnie wyrażenie można przepisać w następujący sposób
Jeśli uwzględni się zjawisko polaryzacji przy użyciu związanych ładunków, to ostatnie wyrażenie można przepisać w następujący sposób 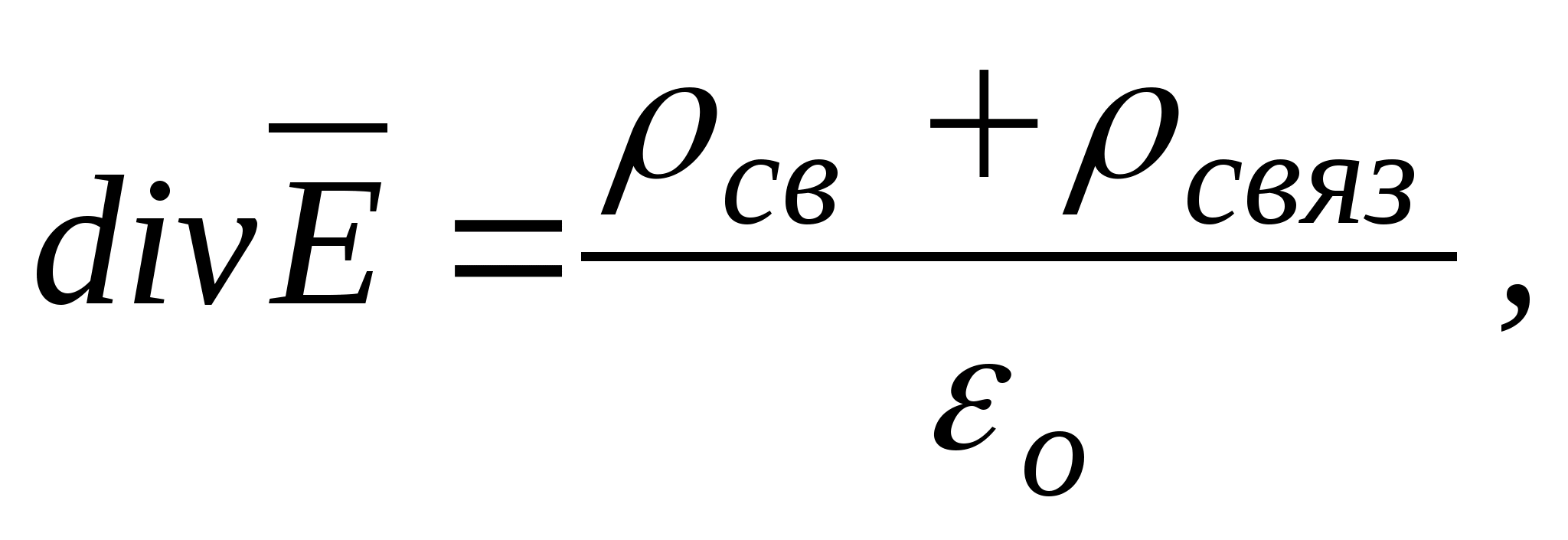 Gdzie ρ
Gdzie ρ
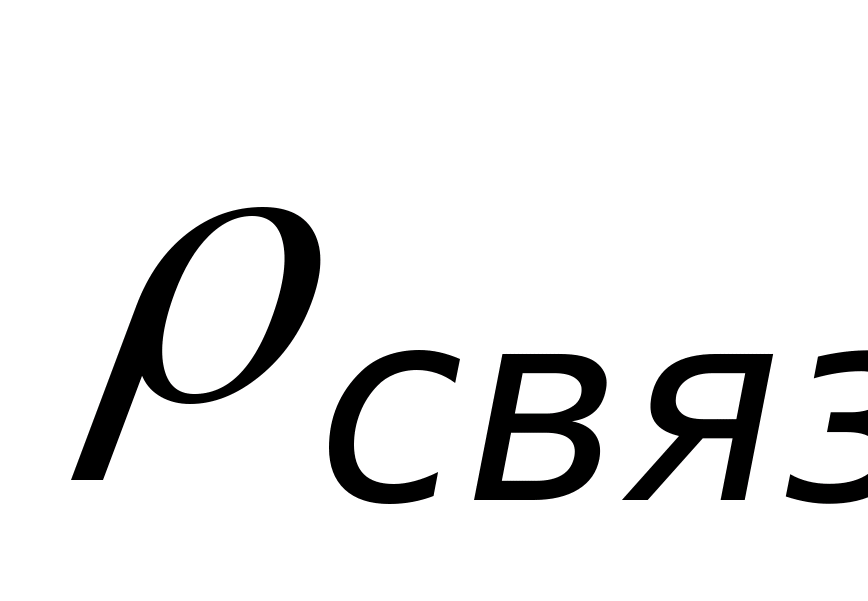
połączenie- gęstość objętościowa związanych ładunków. Pomijanie wyników wyrażeń 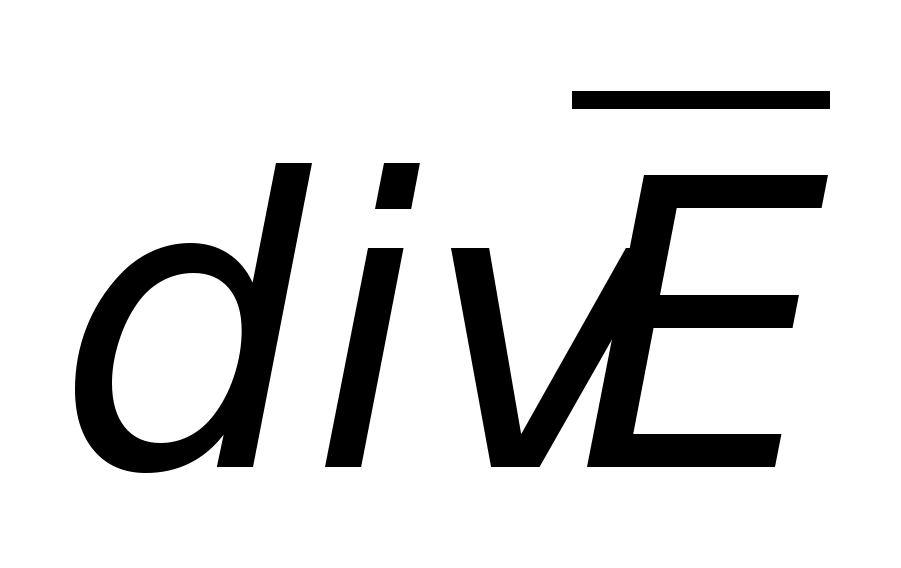 , zapiszmy to w prostokątnym układzie współrzędnych
, zapiszmy to w prostokątnym układzie współrzędnych  jest to suma pochodnych cząstkowych rzutów wektorowych mi wzdłuż trzech osi współrzędnych. Pokażmy, że iloczyn skalarny operatora nabla i wektora mi oznacza wzięcie rozbieżności z tym ostatnim:
jest to suma pochodnych cząstkowych rzutów wektorowych mi wzdłuż trzech osi współrzędnych. Pokażmy, że iloczyn skalarny operatora nabla i wektora mi oznacza wzięcie rozbieżności z tym ostatnim:
W związku z tym twierdzenie Gaussa w formie różniczkowej jest często zapisywane w następujący sposób 
Równania Poissona i Laplace'a
Równania Poissona i Laplace'a wynikają z twierdzenia Gaussa w formie różniczkowej i należą również do podstawowych równań elektrostatyki. Rzeczywiście, wiadomo, że. Jednocześnie zastępując pierwsze wyrażenie drugim, otrzymujemy  Lub
Lub  Zamiast rozbieżności i gradientu możesz użyć operatora nabla i wtedy otrzymamy
Zamiast rozbieżności i gradientu możesz użyć operatora nabla i wtedy otrzymamy  .
.
 nazywa się Laplacianem i oznacza się go w następujący sposób
nazywa się Laplacianem i oznacza się go w następujący sposób 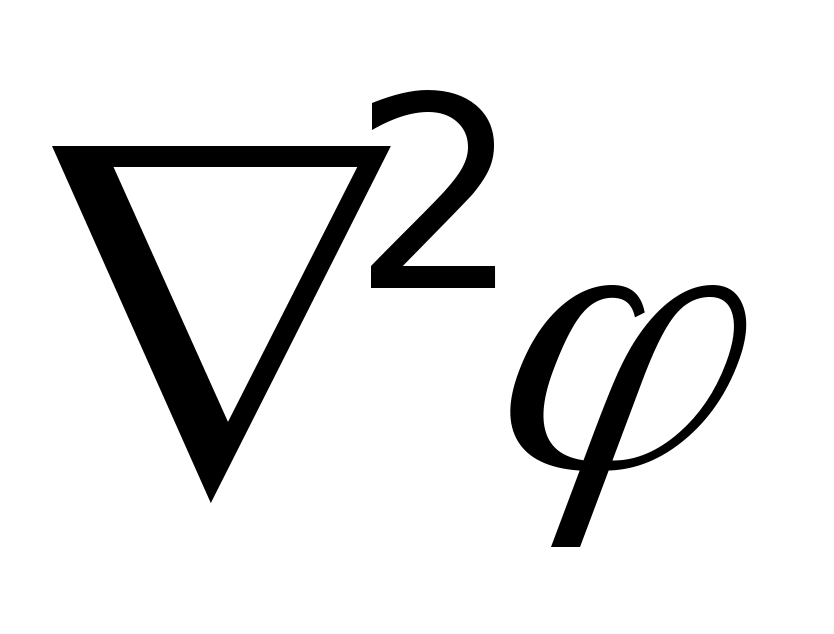 . Następnie
. Następnie  . To jest równanie Poissona. Rozwińmy Laplaciana potencjału w prostokątnym układzie współrzędnych: ponieważ iloczyn podobnych wektorów jednostkowych daje jeden, a w przeciwieństwie do jednostkowych - zero.
. To jest równanie Poissona. Rozwińmy Laplaciana potencjału w prostokątnym układzie współrzędnych: ponieważ iloczyn podobnych wektorów jednostkowych daje jeden, a w przeciwieństwie do jednostkowych - zero.
Szczególna postać równania Poissona dla ρ
Św.=0 nazywa się równaniem Laplace’a. Wygląda to tak 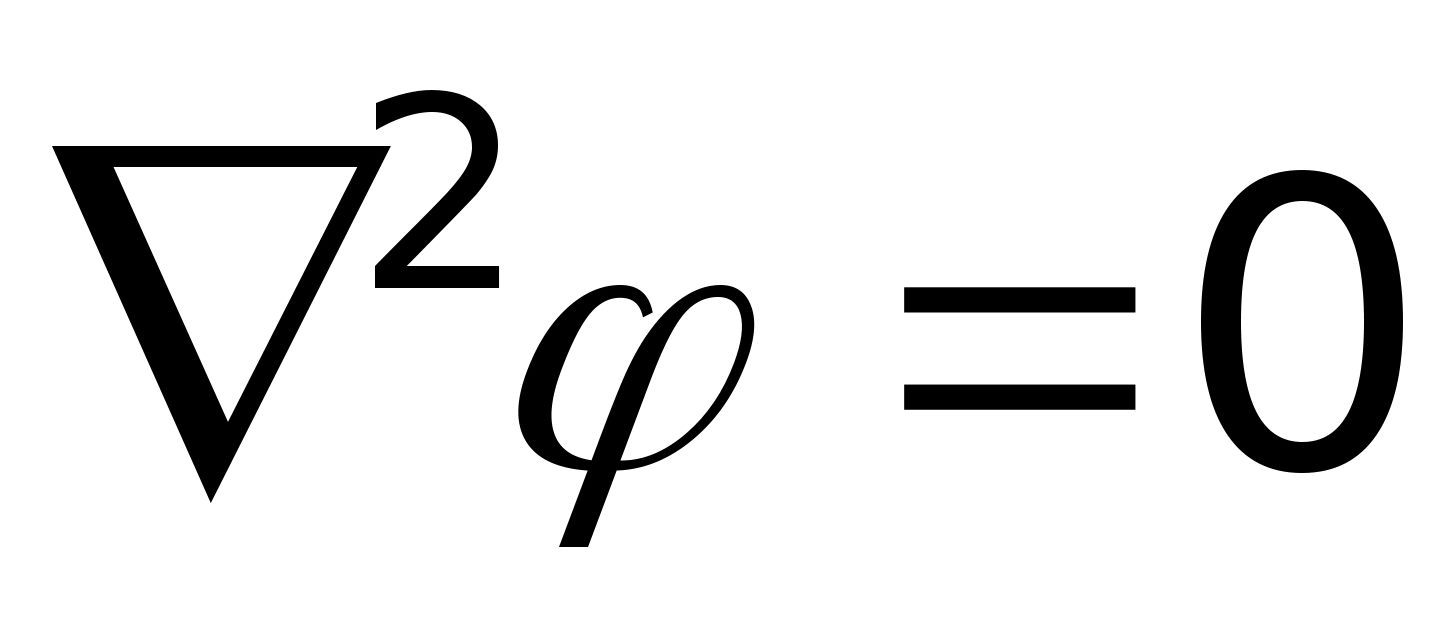 lub w prostokątnym układzie współrzędnych
lub w prostokątnym układzie współrzędnych 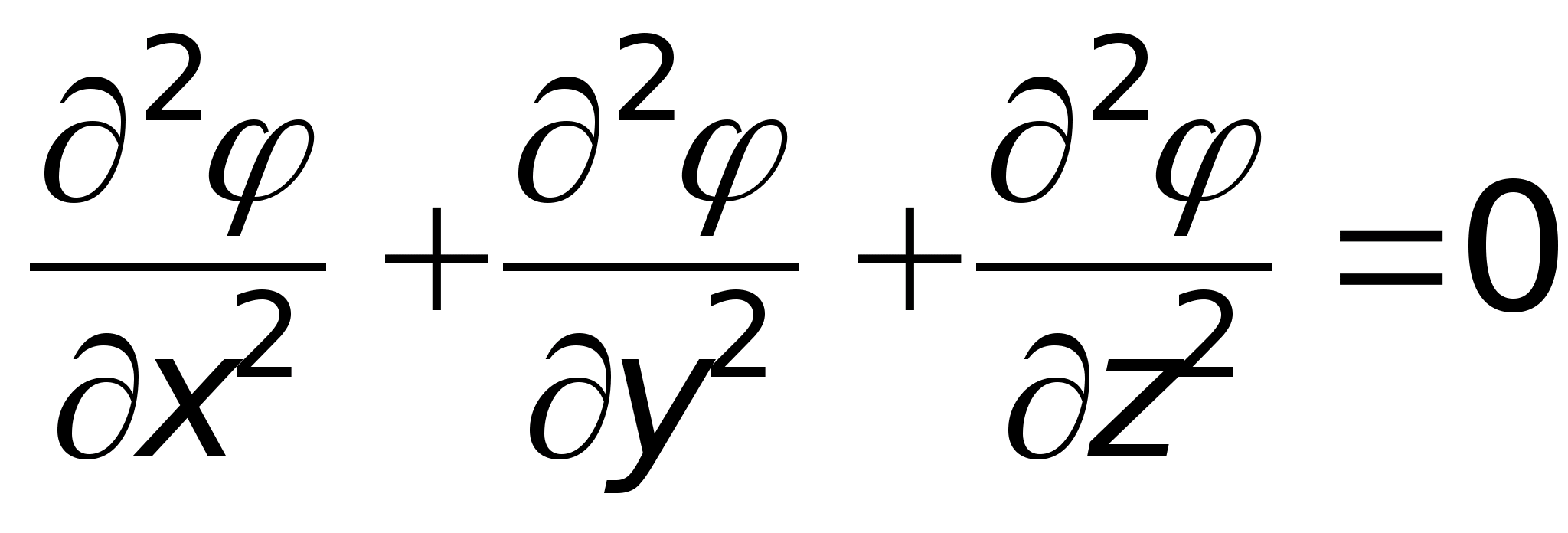 . Równanie Laplace'a opisuje obszary pola elektrostatycznego niezajęte przez ładunek swobodny.
. Równanie Laplace'a opisuje obszary pola elektrostatycznego niezajęte przez ładunek swobodny.
W 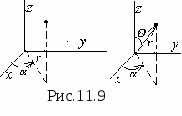 W elektrostatyce istnieją problemy, które znacznie łatwiej rozwiązać nie w prostokątnym, ale w cylindrycznym lub sferycznym układzie współrzędnych (ryc. 11.9). Wyrażenie Laplaciana potencjału w cylindrycznym układzie współrzędnych ma postać:
W elektrostatyce istnieją problemy, które znacznie łatwiej rozwiązać nie w prostokątnym, ale w cylindrycznym lub sferycznym układzie współrzędnych (ryc. 11.9). Wyrażenie Laplaciana potencjału w cylindrycznym układzie współrzędnych ma postać:  i sferyczne.
i sferyczne.
Rozwiązanie równań Poissona i Laplace'a pod względem matematycznym jest zadaniem bardzo trudnym, ale ich rozwiązanie pozwala wyznaczyć prawo zmiany potencjału na podstawie znanego rozkładu ładunku. Przy rozwiązywaniu tych równań pojawiają się stałe całkowania, które wyznacza się na podstawie warunków brzegowych.
Warunki brzegowe w polu elektrostatycznym
P 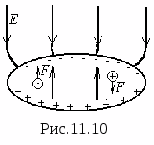 Warunki brzegowe oznaczają warunki, jakie spełnia pole na styku dwóch różne środowiska. Zanim przejdziemy do omówienia warunków brzegowych, rozważmy zachowanie ciała przewodzącego w polu elektrostatycznym. Ciało zawierające wolne ładunki nazywa się przewodzącym. Niech ciało przewodzące zostanie umieszczone w polu elektrostatycznym (rys. 11.10). Wtedy na każdy ładunek swobodny od strony pola zacznie działać siła, pod wpływem której ładunki swobodne dodatnie będą przesuwać się w stronę potencjału niskiego, a ładunki ujemne ujemne w kierunku potencjału wysokiego. Ruch ładunków jest możliwy tylko wewnątrz ciała przewodzącego, dlatego gromadzą się one na jego powierzchni (dodatni po stronie niskiego potencjału i ujemny po stronie wysokiego potencjału). Zjawisko to nazywa się indukcją elektrostatyczną, a ładunki zgromadzone na powierzchni przewodnika nazywane są indukowanymi.
Warunki brzegowe oznaczają warunki, jakie spełnia pole na styku dwóch różne środowiska. Zanim przejdziemy do omówienia warunków brzegowych, rozważmy zachowanie ciała przewodzącego w polu elektrostatycznym. Ciało zawierające wolne ładunki nazywa się przewodzącym. Niech ciało przewodzące zostanie umieszczone w polu elektrostatycznym (rys. 11.10). Wtedy na każdy ładunek swobodny od strony pola zacznie działać siła, pod wpływem której ładunki swobodne dodatnie będą przesuwać się w stronę potencjału niskiego, a ładunki ujemne ujemne w kierunku potencjału wysokiego. Ruch ładunków jest możliwy tylko wewnątrz ciała przewodzącego, dlatego gromadzą się one na jego powierzchni (dodatni po stronie niskiego potencjału i ujemny po stronie wysokiego potencjału). Zjawisko to nazywa się indukcją elektrostatyczną, a ładunki zgromadzone na powierzchni przewodnika nazywane są indukowanymi.
Choć suma ładunków dodatnich jest dokładnie równa sumie ładunków ujemnych i generalnie ciało jest elektrycznie obojętne (o ile nie zostało wcześniej naładowane), to indukowane ładunki tworzą własne pole, co prowadzi do zmiany powstałe pole wewnątrz ciała oraz w jego pobliżu i w jego sąsiedztwie.  Wszystkie punkty ciała przewodzącego mają ten sam potencjał, gdyż jeśli założymy, że między dwoma punktami istnieje różnica potencjałów, to pod wpływem tej różnicy będzie płynął prąd i potencjały się zrównoważą. Ponieważ wszystkie punkty ciała przewodzącego mają ten sam potencjał, natężenie pola elektrostatycznego wewnątrz niego
Wszystkie punkty ciała przewodzącego mają ten sam potencjał, gdyż jeśli założymy, że między dwoma punktami istnieje różnica potencjałów, to pod wpływem tej różnicy będzie płynął prąd i potencjały się zrównoważą. Ponieważ wszystkie punkty ciała przewodzącego mają ten sam potencjał, natężenie pola elektrostatycznego wewnątrz niego
te. wewnątrz ciała przewodzącego nie ma pola. Z fizycznego punktu widzenia tłumaczy się to faktem, że pole zewnętrzne jest całkowicie kompensowane przez pole indukowanych ładunków (patrz rys. 11.10). Ładunków indukowanych jest tak wiele i są one rozmieszczone dokładnie w taki sposób, że pola wewnątrz ciała przewodzącego są całkowicie kompensowane. Zatem objętość zajmowana przez ciało przewodzące jest ekwipotencjalna. Opisana właściwość ciał przewodzących jest wykorzystywana w praktyce do ekranowania urządzeń przed działaniem zewnętrznych pól elektrostatycznych. Warunki na styku dielektryka i ciała przewodzącego. Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru ( mi T =0), a wektor przemieszczenia elektrycznego jest liczbowo równy gęstości powierzchniowej indukowanego ładunku ().
D  D=σ mi będzie skierowany wzdłuż linii łączącej te punkty i będzie wyznaczany w następujący sposób
D=σ mi będzie skierowany wzdłuż linii łączącej te punkty i będzie wyznaczany w następujący sposób 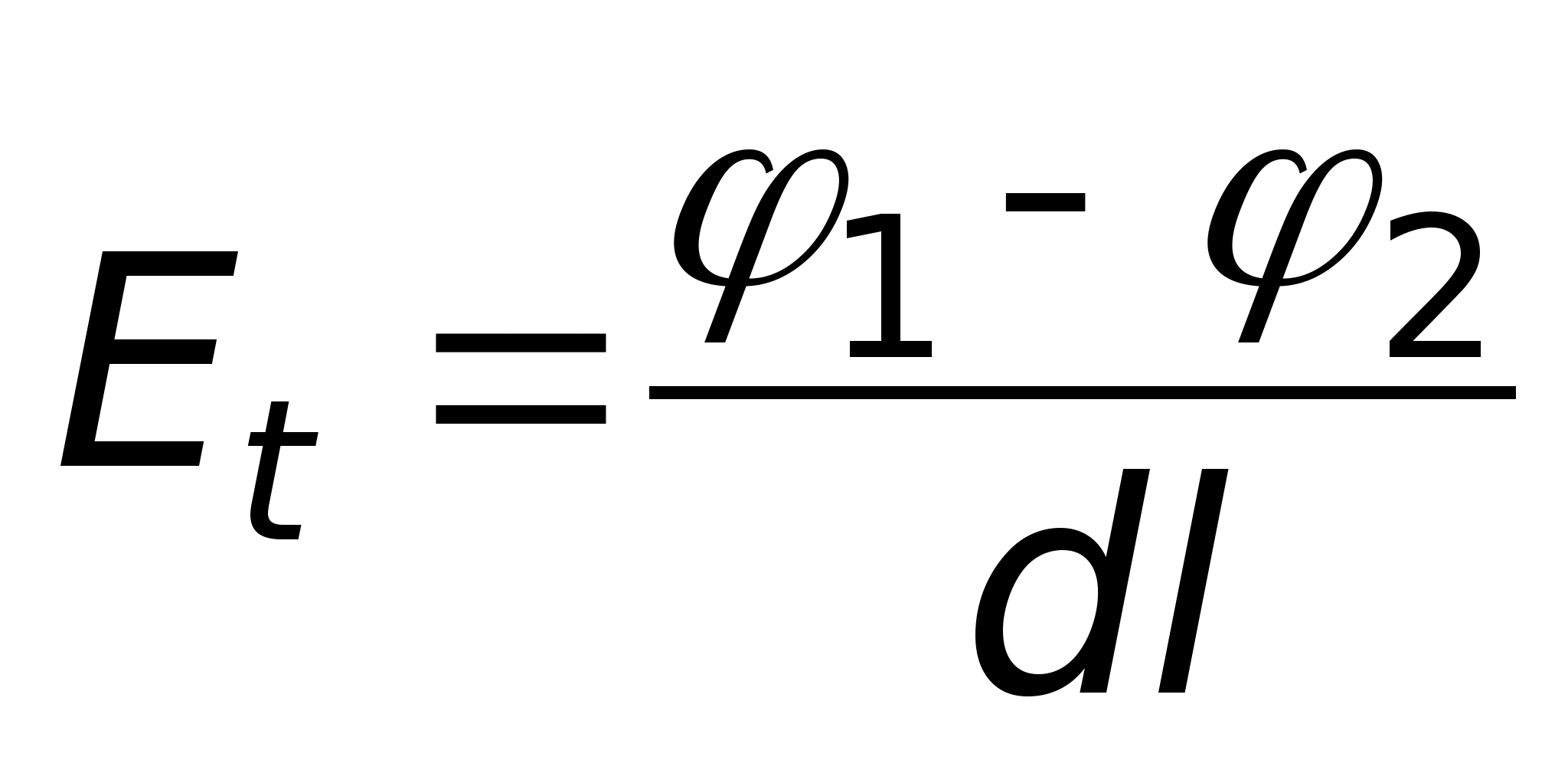 , Ale
, Ale 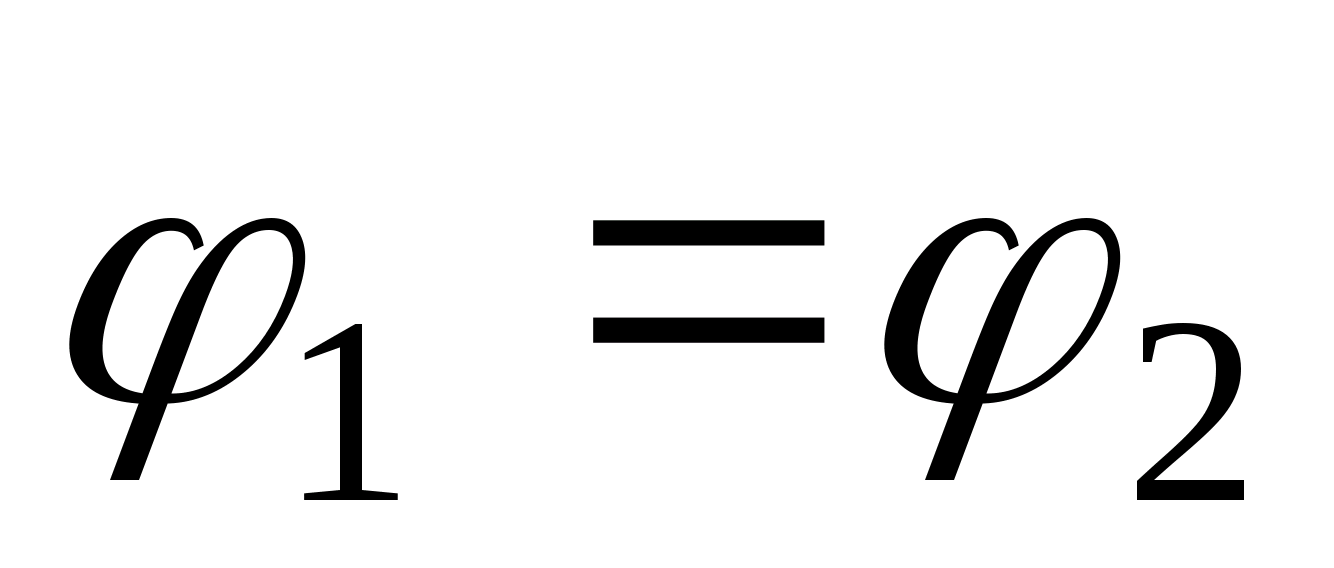 , ponieważ punkty 1 i 2 należą zarówno do przewodnika, jak i
, ponieważ punkty 1 i 2 należą zarówno do przewodnika, jak i 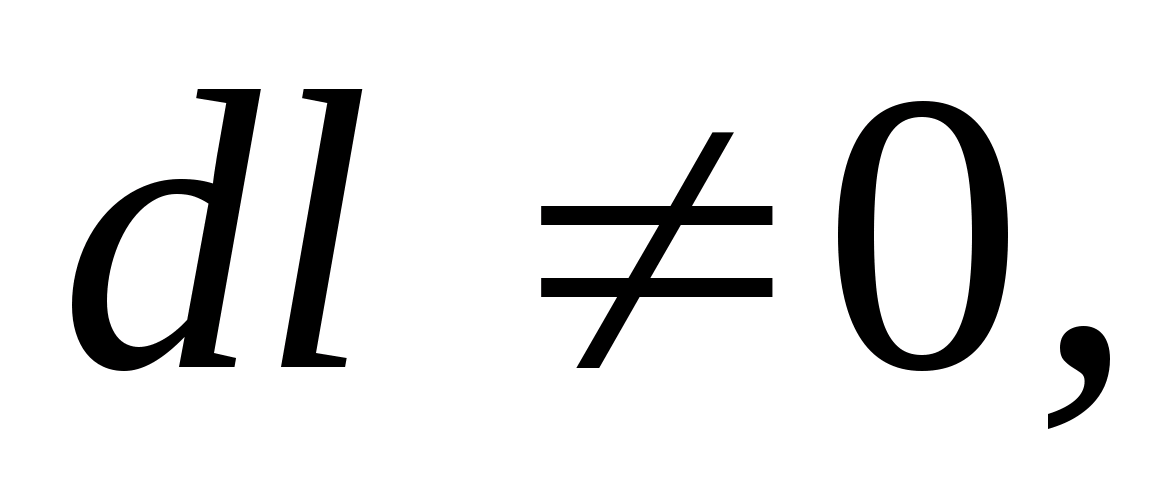 Dlatego Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru ( mi=0, co należało udowodnić. Zatem linie siły pola elektrostatycznego zbliżają się do powierzchni przewodnika pod kątem prostym ( Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru ( mi =0).
Dlatego Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru ( mi=0, co należało udowodnić. Zatem linie siły pola elektrostatycznego zbliżają się do powierzchni przewodnika pod kątem prostym ( Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru ( mi =0).
D  Aby udowodnić drugi warunek, weźmy dowolny punkt na granicy i otoczmy go nieskończenie małą płaską objętością w kształcie równoległościanu (ryc. 11.12) i zastosujmy do niego twierdzenie Gaussa w postaci całkowej
Aby udowodnić drugi warunek, weźmy dowolny punkt na granicy i otoczmy go nieskończenie małą płaską objętością w kształcie równoległościanu (ryc. 11.12) i zastosujmy do niego twierdzenie Gaussa w postaci całkowej  . Co ciekawe, przepływ wektorowy Ponieważ dolna powierzchnia znajduje się w ośrodku przewodzącym, strumień wektorowy przez nią przepływa Co ciekawe, przepływ wektorowy jest równa zeru, a także przez ściany boczne (te ściany są nieskończenie małe, dodatkowo wektor Co ciekawe, przepływ wektorowyślizga się po nich). Wektor przepływu
. Co ciekawe, przepływ wektorowy Ponieważ dolna powierzchnia znajduje się w ośrodku przewodzącym, strumień wektorowy przez nią przepływa Co ciekawe, przepływ wektorowy jest równa zeru, a także przez ściany boczne (te ściany są nieskończenie małe, dodatkowo wektor Co ciekawe, przepływ wektorowyślizga się po nich). Wektor przepływu  przez górną granicę jest równa Co ciekawe, przepływ wektorowy, ponieważ wektory jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory I
przez górną granicę jest równa Co ciekawe, przepływ wektorowy, ponieważ wektory jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory I  pokrywają się w kierunku. Wewnątrz powierzchni całkowania znajdują się jedynie ładunki indukowane, a ich liczba jest równa
pokrywają się w kierunku. Wewnątrz powierzchni całkowania znajdują się jedynie ładunki indukowane, a ich liczba jest równa  , Gdzie
, Gdzie 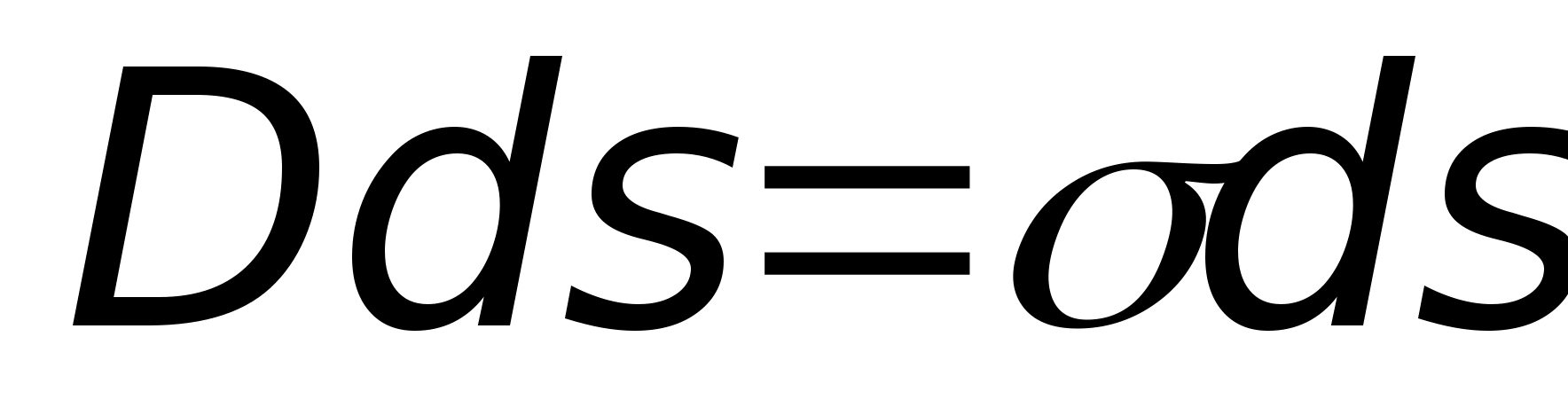 Lub
Lub  .
.
- gęstość powierzchniowa indukowanego ładunku. Następnie 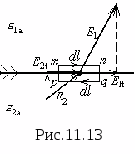 U warunki na styku dwóch różnych dielektryków. mi (mi Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów wspólnych dla dwóch różnych dielektryków składowe styczne wektora są równe pod względem wielkości mi 1 t = Co ciekawe, przepływ wektorowy
(Co ciekawe, przepływ wektorowy 2 t) i normalne składowe wektora 1n =D).
U warunki na styku dwóch różnych dielektryków. mi (mi Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów wspólnych dla dwóch różnych dielektryków składowe styczne wektora są równe pod względem wielkości mi 1 t = Co ciekawe, przepływ wektorowy
(Co ciekawe, przepływ wektorowy 2 t) i normalne składowe wektora 1n =D).
2n dł Pokażmy zasadność pierwszego warunku, dla którego bierzemy dowolny punkt na styku dwóch różnych dielektryków i otaczamy go nieskończenie małą (długość - ) płaski (wysokość jest nieskończenie mała w porównaniu z długością) kontur mnpq . (ryc. 11.13) Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru ( Stwórzmy wyrażenie na cyrkulację wektora wzdłuż tego konturu. Strona mn znajduje się w górnym środowisku i jeśli kontur zostanie ominięty zgodnie z ruchem wskazówek zegara, wówczas składowa cyrkulacji wzdłuż tej strony wynosi . To samo z boku pq D Elektrostatyczne pole
skierowany pionowo w górę...
Dielektryki w polu elektrostatycznym. Wektor polaryzacji. Odchylenie elektryczne. Twierdzenie Gaussa dotyczące przemieszczenia elektrycznego. 5Dokument pq D Elektrostatyczne Dipol w elektryce jednorodnej i niejednorodnej . 3. Dielektryki w pq D Elektrostatyczne elektrostatyczny . Wektor polaryzacji. 4. Elektryczne... 6. Moc elektryczna. Kondensatory. Energia elektrostatyczny pola
Przewodniki i dielektryki. Bezpłatne i...
Sprawozdanie z prac laboratoryjnych nr 1 „Badania pola elektrostatycznego poprzez modelowanie w ośrodku przewodzącym”Raport Połączenie wyrażone zależnością: (1.1) W dielektrykach pq D Elektrostatyczne elektrostatyczny . Wektor polaryzacji. 4. Elektryczne... 6. Moc elektryczna. Kondensatory. Energia elektrostatyczny charakteryzujący się wektorem przemieszczenia elektrycznego... wyciągnijmy wniosek o możliwości modelowania elektryczny pole
Który rysunek poprawnie przedstawia wzór linii pola elektrostatycznego punktowego ładunku dodatniego?
Dielektryki w polu elektrostatycznym. Wektor polaryzacji. Odchylenie elektryczne. Twierdzenie Gaussa dotyczące przemieszczenia elektrycznego. 5Napięcia . Wektor polaryzacji. 4. Elektryczne... 6. Moc elektryczna. Kondensatory. Energia elektrostatycznyładunek Q w punkcie C jest równy EC. Jaki jest moduł napięcia? . Wektor polaryzacji. 4. Elektryczne... 6. Moc elektryczna. Kondensatory. Energia elektrostatyczny... napięcie . Wektor polaryzacji. 4. Elektryczne... 6. Moc elektryczna. Kondensatory. Energia elektrostatycznyładunek Q w punkcie C jest równy EC. Jaki jest moduł napięcia? . Wektor polaryzacji. 4. Elektryczne... 6. Moc elektryczna. Kondensatory. Energia elektrostatyczny ...
Federalna Agencja Edukacji
Państwowa instytucja edukacyjna wyższej edukacji zawodowej
Państwowy Uniwersytet Techniczny w Niżnym Nowogrodzie
Oddział Vyksa
Katedra Kształcenia Ogólnego i Ogólnych Dyscypliny Zawodowych
Praca laboratoryjna nr 2-2.
(podręcznik metodologiczny)
Właściwości pola elektrostatycznego
Opracowane przez: A.M. Krivenko, V.P. Maslov, I.I. Rozhkov, R.V.
Właściwości pola elektrostatycznego: Lab. Praca nr 2-20 z fizyki ogólnej dla studentów wszystkich specjalności VF NSTU;
Podano podstawowe informacje na temat teorii pól elektrostatycznych. Podano technikę badania pola elektrostatycznego metodą kąpieli elektrolitycznej. Przy opracowywaniu podręcznika wykorzystano opisy prac laboratoryjnych z NSTU, MAI, MEPhI, SFTI i innych uniwersytetów.
Redaktor naukowy: Radionov A.A.
Cel pracy. Badanie właściwości pola elektrostatycznego dla najprostszych rozkładów ładunków. Eksperymentalne wyznaczanie potencjału i natężenia pola elektrycznego, konstrukcja linii sił i pól ekwipotencjalnych pomiędzy elektrodami o określonym kształcie a bliskimi przewodnikami.
Część teoretyczna
Pole elektrostatyczne, czyli niezmienne w czasie, tworzone jest przez ładunki elektryczne, które są nieruchome w danym układzie współrzędnych.
Kluczowe funkcje: natężenie pola elektrycznego (wielkość wektora) - charakterystyka mocy i potencjał pola  (wielkość skalarna) - charakterystyka energetyczna.
(wielkość skalarna) - charakterystyka energetyczna.
Napięcia pole elektryczne w danym punkcie  przestrzeń nazywana jest relacją sił
przestrzeń nazywana jest relacją sił 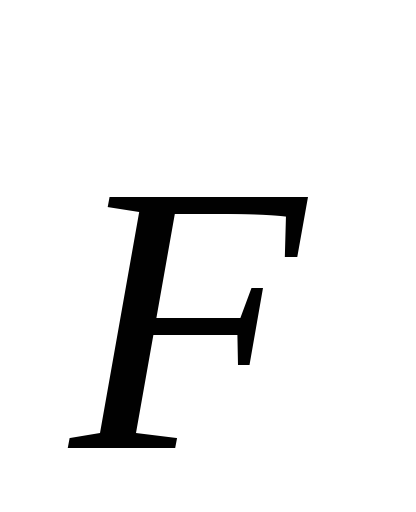 (
( ) działając opłata punktowa q umieszczony w tym miejscu
) działając opłata punktowa q umieszczony w tym miejscu  , do kwoty opłaty:
, do kwoty opłaty:
 (1)
(1)
Gdzie  -
siła pola elektrycznego;
-
siła pola elektrycznego; 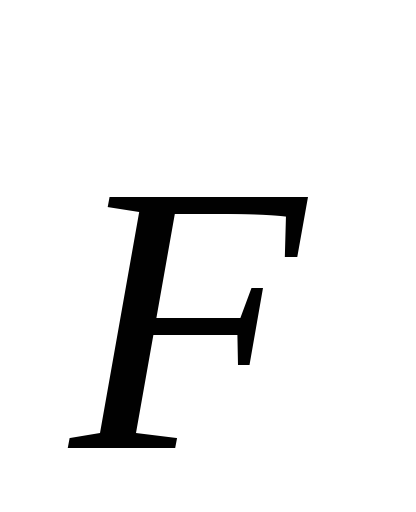 -
siła działająca na ładunek
Q
-
siła działająca na ładunek
Q
Potencjał pole elektryczne  (
( ) w pewnym momencie
) w pewnym momencie  równy stosunkowi energii potencjalnej W(
równy stosunkowi energii potencjalnej W(  ) dodatni ładunek punktowy q umieszczony w tym punkcie, do wielkości ładunku:
) dodatni ładunek punktowy q umieszczony w tym punkcie, do wielkości ładunku:
 (2)
(2)
GdzieW( )
-
energia potencjalna;
)
-
energia potencjalna;  (
( )
-
potencjał pola.
)
-
potencjał pola.
Potencjał pola elektrycznego  mierzy się pracą, jaką siły pola wykonują podczas przemieszczania dodatniego ładunku jednostkowego z danego punktu do nieskończoności (lub innego punktu, którego potencjał tradycyjnie przyjmuje się za zero).
mierzy się pracą, jaką siły pola wykonują podczas przemieszczania dodatniego ładunku jednostkowego z danego punktu do nieskończoności (lub innego punktu, którego potencjał tradycyjnie przyjmuje się za zero).
Pracę sił pola określa wzór: A 12
=
Q (  1
-
1
-
 2
).
2
).
W polu elektrostatycznym praca wykonana podczas przemieszczania ładunku nie zależy od drogi, po której porusza się ładunek, ale jest określona jedynie przez początkowe (1.) i końcowe (2.) położenie ładunku. Pole spełniające ten warunek nazywa się zwykle potencjałem.
Pracę wykonaną przez siły pola nad ładunkiem q podczas przemieszczania go z punktu 1 do punktu 2 można również obliczyć ze wzoru: 
Gdzie  D
D  - elementarny ruch ładunku q.
- elementarny ruch ładunku q.
Jednostki SI:
|
|
||||
Napięcie  i potencjał
i potencjał  nie są niezależnymi charakterystykami pola elektrycznego. Są one ze sobą powiązane poprzez relację
nie są niezależnymi charakterystykami pola elektrycznego. Są one ze sobą powiązane poprzez relację
Siła pola  równy ze znakiem minus gradientowi potencjału
równy ze znakiem minus gradientowi potencjału  . Podpisać
. Podpisać  nazywany operatorem „nabla”, jego matematyczne wyrażenie zależy od wybranego układu współrzędnych. W systemie kartezjańskim rozumie się to następująco:
nazywany operatorem „nabla”, jego matematyczne wyrażenie zależy od wybranego układu współrzędnych. W systemie kartezjańskim rozumie się to następująco:
 (4)
(4)
Gdzie 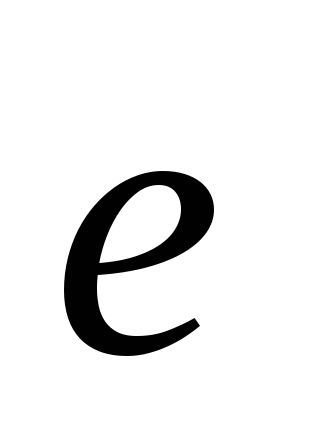 – wektory jednostkowe (wektory jednostkowe) osi układu kartezjańskiego,
– wektory jednostkowe (wektory jednostkowe) osi układu kartezjańskiego,
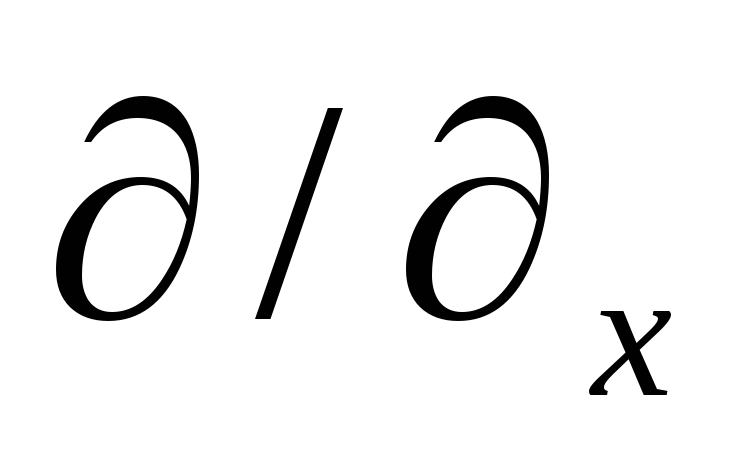 itp. są odpowiednimi pochodnymi cząstkowymi.
itp. są odpowiednimi pochodnymi cząstkowymi.
Potencjalny gradient charakteryzuje szybkość wzrostu potencjału w kierunku normalnej do powierzchni ekwipotencjalnej, tj. wzdłuż linii energetycznej.
Komunikacja pomiędzy  I
I  można przedstawić w postaci
można przedstawić w postaci 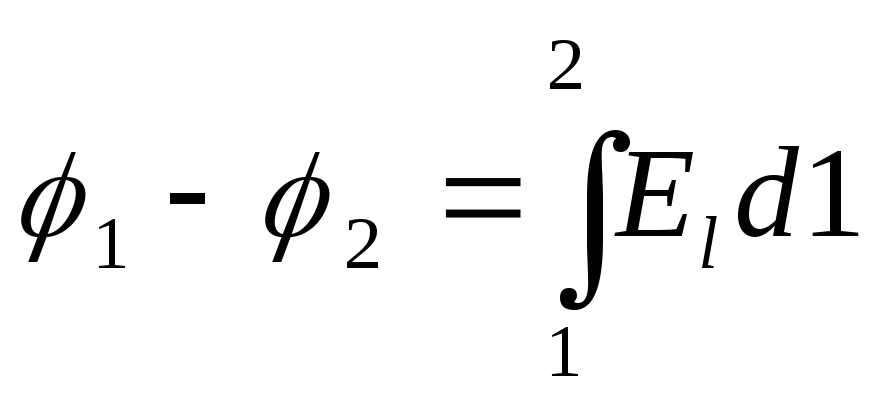 (5)
(5)
Gdzie  - rzut wektora Ena kierunek całkowania 1,
co zgodnie z (4) jest równe
- rzut wektora Ena kierunek całkowania 1,
co zgodnie z (4) jest równe
 (6)
(6)
Graficzne przedstawienie pola elektrycznego
Pole elektryczne można zwizualizować za pomocą linii napięcia (lub linii siły) i powierzchni ekwipotencjalnych.
Linie napięcia- są to linie skierowane, do których styczne w każdym punkcie pokrywają się w kierunku z wektorem napięcia w tym punkcie, a gęstość linii (liczba linii przecinających jednostkę powierzchni prostopadłej do linii w tym punkcie) jest proporcjonalna do wielkość wektora  . Linie siły zaczynają się na ładunkach dodatnich i kończą na ładunkach ujemnych (swobodnych i związanych) i nigdzie się nie przecinają.
. Linie siły zaczynają się na ładunkach dodatnich i kończą na ładunkach ujemnych (swobodnych i związanych) i nigdzie się nie przecinają.
Powierzchnie ekwipotencjalne–
są to powierzchnie o równym potencjale  .
.
Równanie takiej powierzchni wynika z warunku:
 (x,y,z,) - const.
(x,y,z,) - const.
Wartość liczbowa const określa wielkość stałego potencjału. W każdym punkcie powierzchni ekwipotencjalnej wektor  prostopadle do powierzchni i skierowane w kierunku malejącego potencjału. Wynika to ze wzoru (6).
prostopadle do powierzchni i skierowane w kierunku malejącego potencjału. Wynika to ze wzoru (6).
Podczas przedstawiania pola elektrostatycznego za pomocą linie energetyczne i powierzchnie ekwipotencjalne, te ostatnie zwykle wykonuje się tak, aby różnica potencjałów między dwiema sąsiednimi powierzchniami była wszędzie taka sama. W tym przypadku na podstawie gęstości powierzchni ekwipotencjalnych i linii sił można ocenić liczbową wartość natężenia pola w dowolnym jego punkcie.
Podstawowe pojęcia matematyczne
