Określa się potencjał pola elektrostatycznego w każdym punkcie. Badanie pola elektrostatycznego
Cel pracy: eksperymentalne badanie właściwości pole elektrostatyczne i wykreślanie położenia linii pola przy użyciu krzywych o równych potencjałach.
Przyrządy i wyposażenie: łaźnia elektrolityczna, oscyloskop, woltomierz, potencjometr, klucz, elektrody różne konfiguracje.
Informacje teoretyczne
Pole elektryczne to rodzaj materii, która przeprowadza interakcję z obiektem nieruchomym ładunki elektryczne. Każdy ładunek ma swoje własne pole elektrostatyczne, które w każdym punkcie przestrzeni charakteryzuje się wektorem napięcia i potencjałem elektrostatycznym φ.
Natężenie pola elektrostatycznego w punkcie jest wektorową wielkością fizyczną, która jest liczbowo równa stosunkowi sił  , działając na ładunek próbny q o , do wartości tego ładunku umieszczonego w danym punkcie pola:
, działając na ładunek próbny q o , do wartości tego ładunku umieszczonego w danym punkcie pola:
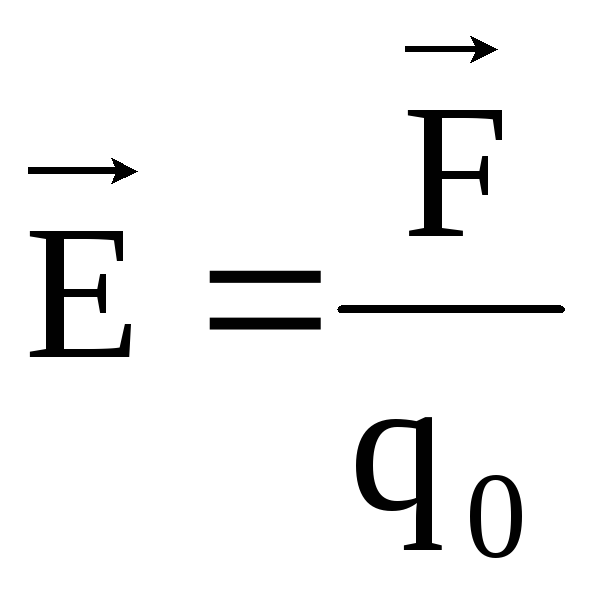 .
(1)
.
(1)
Jeżeli ładunek próbny q o =+l, to  Zatem wektor natężenia pola elektrostatycznego jest równy sile działającej na jednostkowy ładunek próbny.
Zatem wektor natężenia pola elektrostatycznego jest równy sile działającej na jednostkowy ładunek próbny.
Kierunek wektora  pokrywa się z kierunkiem siły. Ze wzoru (1) wynika, że jednostką natężenia pola elektrycznego jest niuton na kulomb (N/C); 1N/C to natężenie pola działającego na ładunek punktowy o wartości 1C z siłą 1N.
pokrywa się z kierunkiem siły. Ze wzoru (1) wynika, że jednostką natężenia pola elektrycznego jest niuton na kulomb (N/C); 1N/C to natężenie pola działającego na ładunek punktowy o wartości 1C z siłą 1N.
Wektor  we wszystkich punktach pola jest ono skierowane promieniowo od ładunku, jeśli jest dodatni, i promieniowo w stronę ładunku, jeśli jest ujemny (ryc. 1).
we wszystkich punktach pola jest ono skierowane promieniowo od ładunku, jeśli jest dodatni, i promieniowo w stronę ładunku, jeśli jest ujemny (ryc. 1).

Pole elektrostatyczne można przedstawić za pomocą linii sił. Linia siły, czyli linia natężenia pola elektrostatycznego, to linia, w każdym punkcie której wektor natężenia jest skierowany stycznie (ryc. 2),
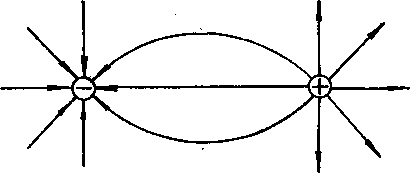
Linie siły zawsze zaczynają się na powierzchni ciał naładowanych dodatnio, a kończą na powierzchni ciał naładowanych ujemnie lub idą w nieskończoność.
Jeżeli pole jest utworzone przez pojedynczy ładunek punktowy q, to praca wykonana przez pole podczas przemieszczania się ładunku próbnego Q o z pozycji 1 do pozycji 2 (ryc. 3), nie zależy od trajektorii ruchu:
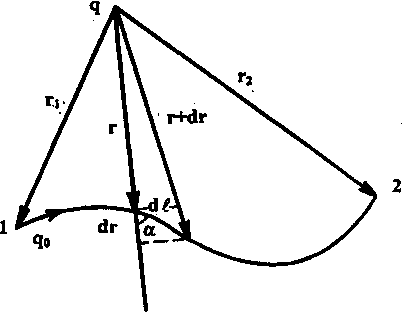
Z wyrażenia (2) jasno wynika, że o pracy decyduje jedynie położenie początkowego 1 i końcowych 2 punktów. Siły, których praca nie zależy od trajektorii ruchu, nazywane są konserwatywnymi. W tym przypadku pole elektryczne jest potencjalne, a wzór ma postać A 1,2 = -ΔW p. Znak minus oznacza, że samo pole wykonuje dodatnią pracę w wyniku spadku energii
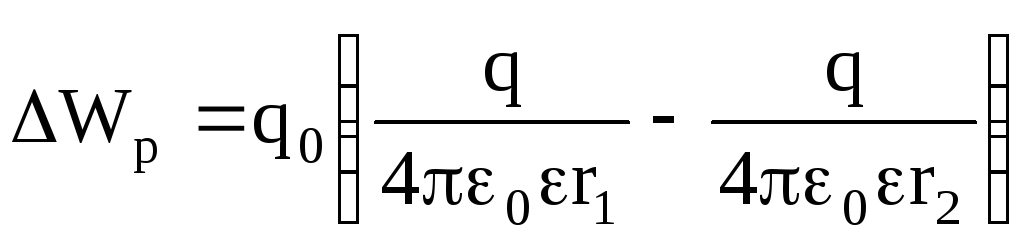 .
(3)
.
(3)
Oznacza to, że energia potencjalna dwóch ładunków punktowych znajdujących się w odległości r,
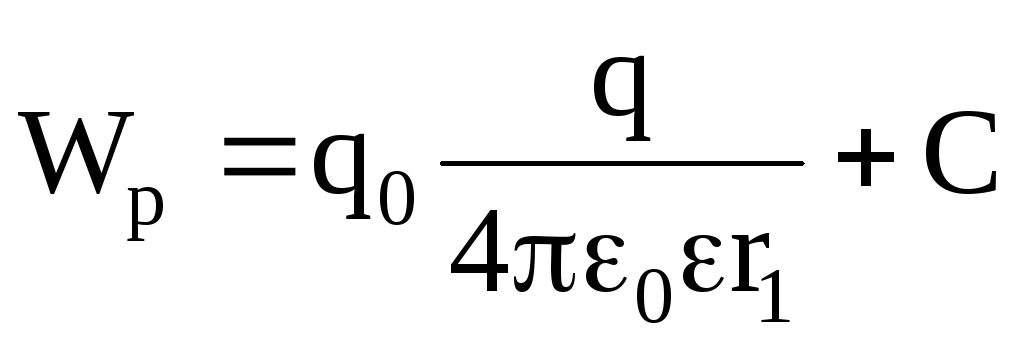 (4)
(4)
Rozmiar 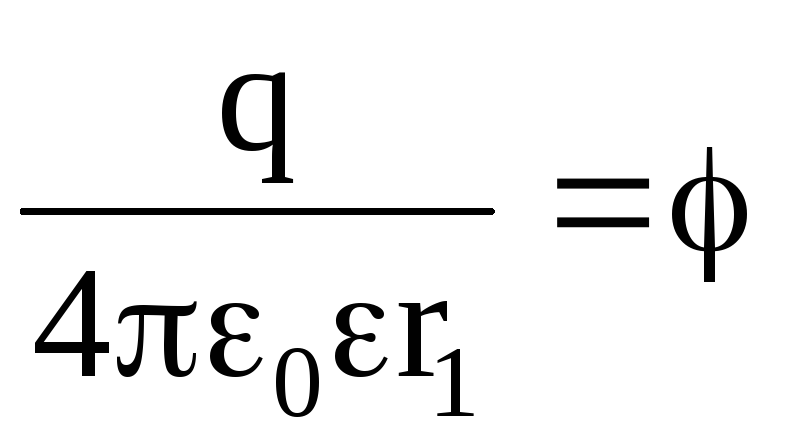 zwany potencjałem pola opłata punktowa. Następnie 4. 0 np
zwany potencjałem pola opłata punktowa. Następnie 4. 0 np
wzór (2) przyjmuje postać
A 1,2 =q 0 (φ 1 -φ 2).
(5) 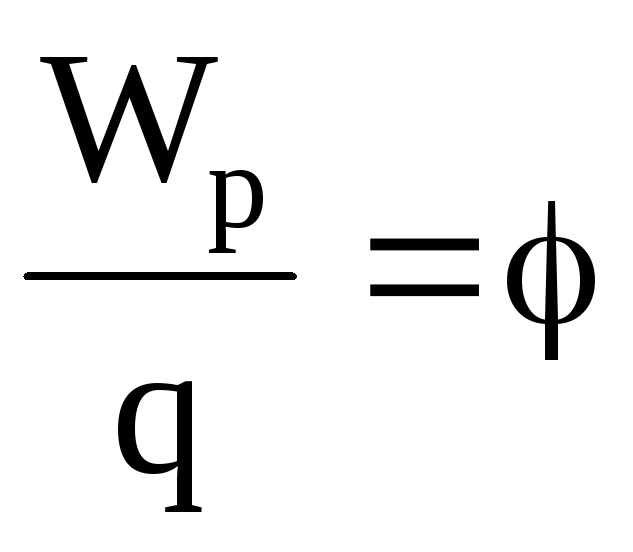 Podstawiając wartości q o =+l i C=0 do (4), otrzymujemy –
. Potencjał danego punktu pola jest wielkością fizyczną liczbowo równą energii potencjalnej jednostkowego ładunku dodatniego umieszczonego w tym punkcie. Potencjał
Podstawiając wartości q o =+l i C=0 do (4), otrzymujemy –
. Potencjał danego punktu pola jest wielkością fizyczną liczbowo równą energii potencjalnej jednostkowego ładunku dodatniego umieszczonego w tym punkcie. Potencjał
charakterystyka energetyczna pola.
Korzystając ze wzorów (2), (4) i (5) równanie na pracę wykonaną przez siły elektryczne podczas przemieszczania ładunku q 0 z punktu 1 do punktu 2 można zapisać w postaci
ZA 1,2 = W p 1 -W p 2 =q 0 (φ 1 -φ 2) . (6)
Praca wykonana podczas przemieszczania ładunku punktowego jest równa iloczynowi tego ładunku i różnicy potencjałów w początkowym i końcowym punkcie toru.
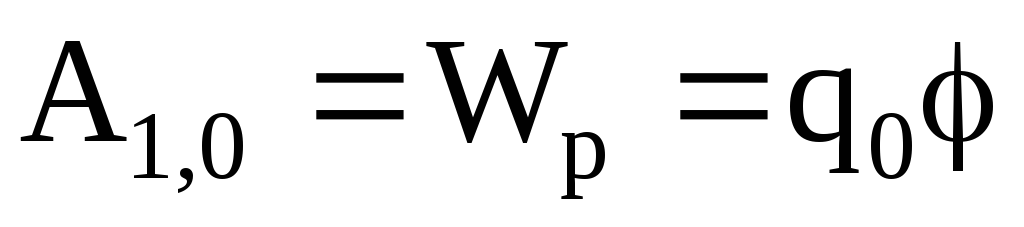 . (7)
. (7)
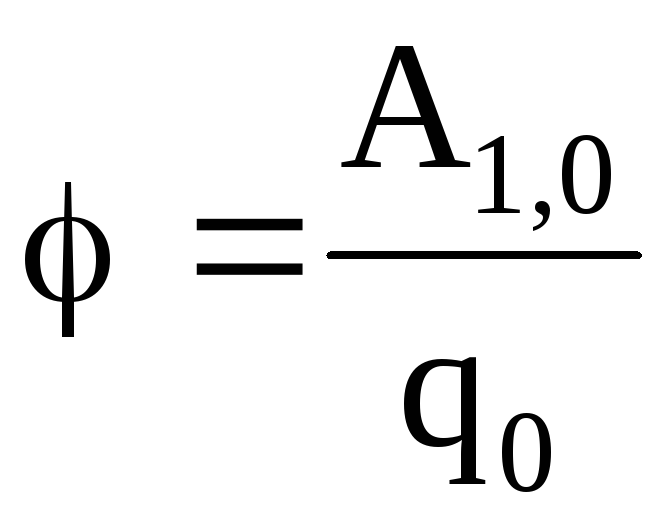 . (8)
. (8)
Jeżeli punkt 2 leży w nieskończoności, to energia potencjalna ładunku q o w nim jest równa zeru (W p 2 = 0), a zatem potencjał pola jest również równy zeru (φ 2 = 0). Następnie zgodnie z (6)
Dlatego potencjał danego punktu pola można zdefiniować jako wielkość fizyczną, która jest liczbowo równa pracy wykonanej przez siły elektryczne podczas przemieszczania jednostkowego ładunku dodatniego z danego punktu do nieskończoności.
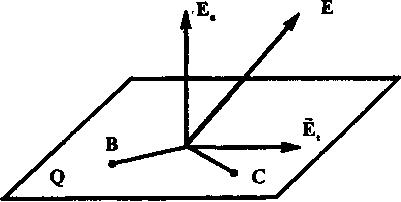
W układzie SI jednostką potencjału jest wolt (V), tj. potencjał takiego punktu pola, aby przenieść z nieskończoności ładunek równy 1 C, należy wykonać 1 J pracy: 1 J = 1 C V. Zatem 1 V=J/C. Geometryczne położenie punktów pola o jednakowych potencjałach nazywa się powierzchnią ekwipotencjalną. Praca wykonana podczas przemieszczania ładunku wzdłuż niego wynosi zero. Wniosek ten wynika z definicji pracy pola, gdy porusza się w nim ładunek: A = q 0 (φ 1 -φ 2), ponieważ φ 1 = φ 2.  Linie pola są zawsze normalne do powierzchni ekwipotencjalnych. Udowodnijmy to przez sprzeczność. Niech Q będzie częścią tej powierzchni (ryc. 4), B i C jej punktami, a wektorem
Linie pola są zawsze normalne do powierzchni ekwipotencjalnych. Udowodnijmy to przez sprzeczność. Niech Q będzie częścią tej powierzchni (ryc. 4), B i C jej punktami, a wektorem
nie jest prostopadła do Q. Ale wtedy musi istnieć E t -  składowa styczna wektora
składowa styczna wektora  , równoległa do powierzchni Q. Oznacza to, że praca na odcinku BC jest różna od zera, co jest niemożliwe. Dlatego wektor
, równoległa do powierzchni Q. Oznacza to, że praca na odcinku BC jest różna od zera, co jest niemożliwe. Dlatego wektor
prostopadle do powierzchni ekwipotencjalnej.
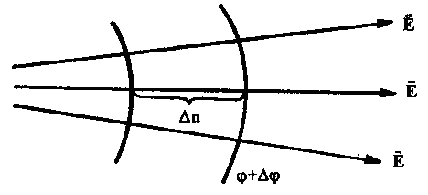
Ustalmy związek pomiędzy napięciem i potencjałem. Z jednej strony pracę przy przenoszeniu ładunku q 0 z powierzchni ekwipotencjalnej o potencjale φ do pobliskiej powierzchni ekwipotencjalnej o potencjale φ + Δφ normalnym do niej (w odległości Δn) oblicza się ze wzoru ΔA = q 0 En (ryc. 5).  z nieskończenie małym przemieszczeniem można uznać za stałe. Natomiast wielkość tej pracy można obliczyć korzystając ze wzoru (5). Zatem,
z nieskończenie małym przemieszczeniem można uznać za stałe. Natomiast wielkość tej pracy można obliczyć korzystając ze wzoru (5). Zatem,
Gdzie 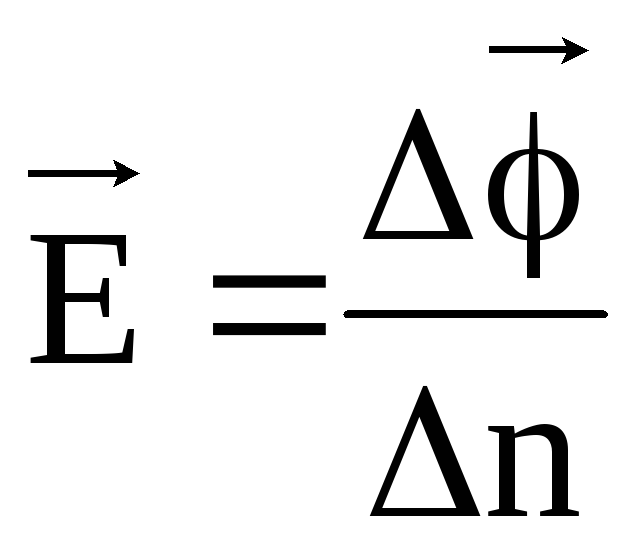 , (9)
, (9)
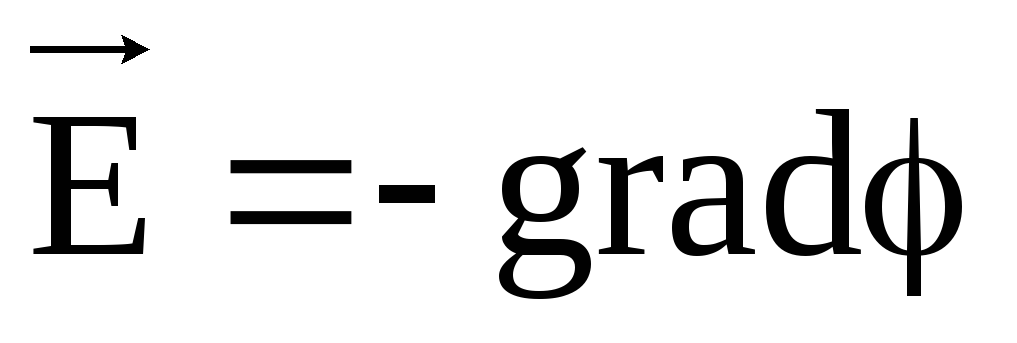 .
.
Znak minus wskazuje, że wektor napięcia jest skierowany w kierunku malejącego potencjału.
Ze wzoru (9) wynika, że jednostką napięcia jest 1N/C=1V/m, gdzie V (wolt) jest jednostką potencjału pola elektrycznego.
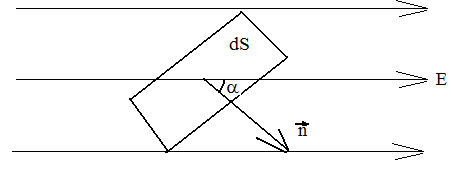
Liczba linii pola przechodzących przez obszar elementarny dS, których normalna n tworzy kąt z kierunkiem wektora E, nazywana jest przepływem natężenia pola elektrycznego przez ten obszar  , (ryc. 7)
, (ryc. 7)
Dla dowolnej zamkniętej powierzchni
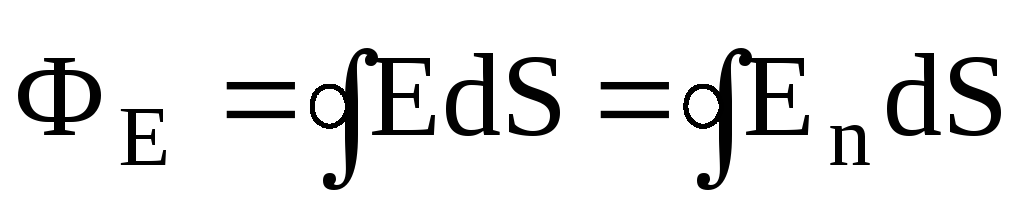 ,
(10)
,
(10)
gdzie E n =Ecos.
Przepływ nie zależy od kształtu i wielkości zamkniętej powierzchni ani od umiejscowienia ładunku w objętości objętej tą powierzchnią.
Strumień wektora natężenia przenikający dowolną zamkniętą powierzchnię otaczającą ładunki elektryczne jest równy algebraicznej sumie ładunków wewnątrz tej powierzchni podzielonej przez 0
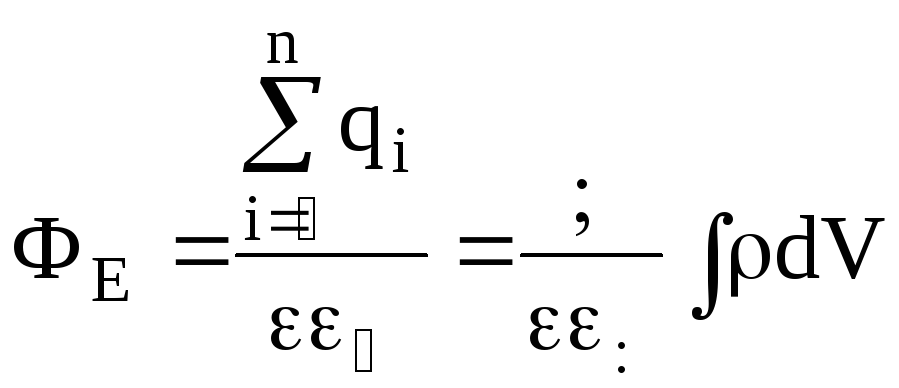 ,
(11)
,
(11)
Gdzie 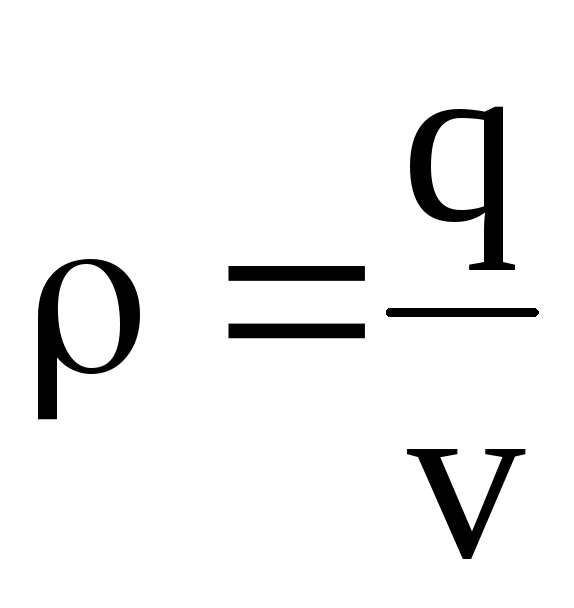 .
.
Stanowisko to nazywa się twierdzeniem Ostrogradskiego-Gaussa
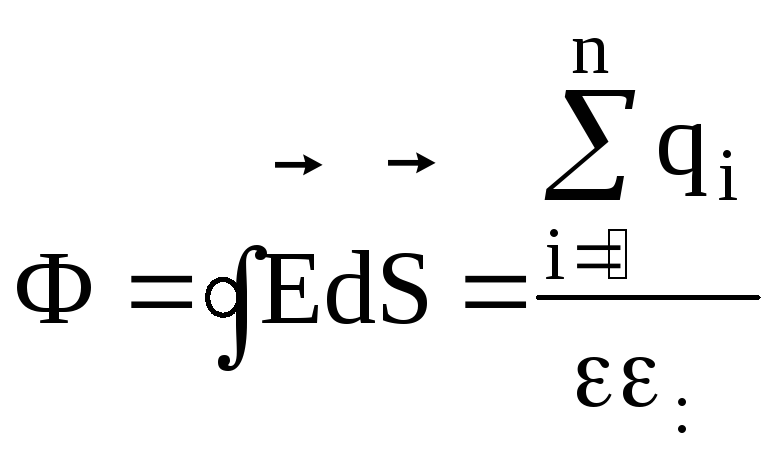 .
(12)
.
(12)
Stosując twierdzenie Ostrogradskiego-Gaussa, trudno jest określić siłę pól wytwarzanych przez naładowane ciała o różnych kształtach.
Siła pola wytworzona przez równomiernie naładowaną nieskończoną płaszczyznę
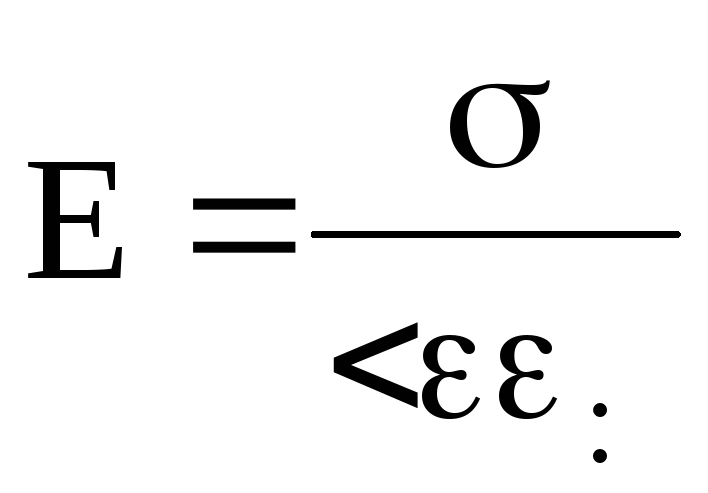 ,
(13)
,
(13)
Gdzie 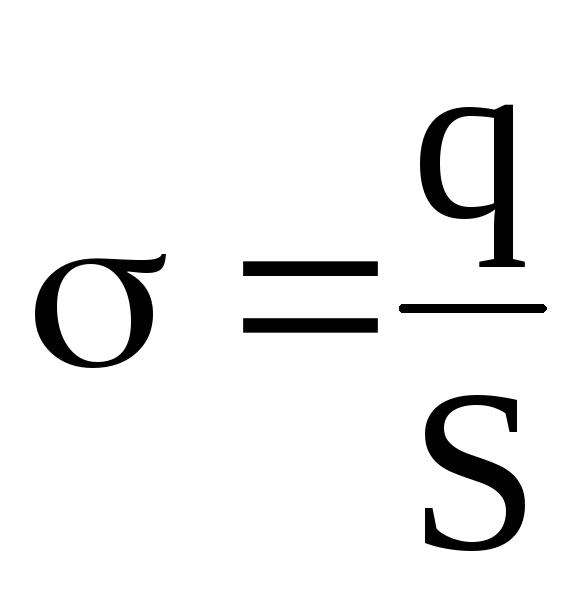 .
.
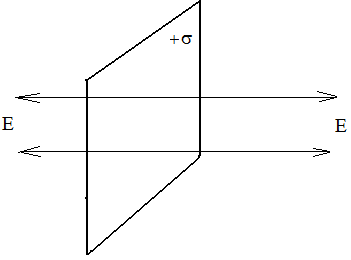
Pole wytworzone przez równomiernie naładowaną nieskończoną płaszczyznę jest jednorodne i nie zależy od odległości od płaszczyzny.
Natężenie pola między dwiema nieskończonymi równoległymi, przeciwnie naładowanymi płaszczyznami.
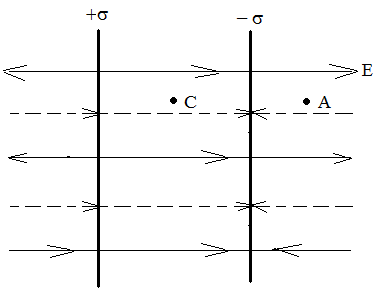
Na ryc. Rysunek 9 przedstawia przekrój pionowy płaszczyzn, pole dodatnio naładowanej płaszczyzny przedstawiono liniami ciągłymi sił, pole ujemnie naładowanej płaszczyzny liniami przerywanymi. Ponieważ gęstości ładunków powierzchniowych płaszczyzn są jednakowe co do wielkości, zgodnie ze wzorem (13)
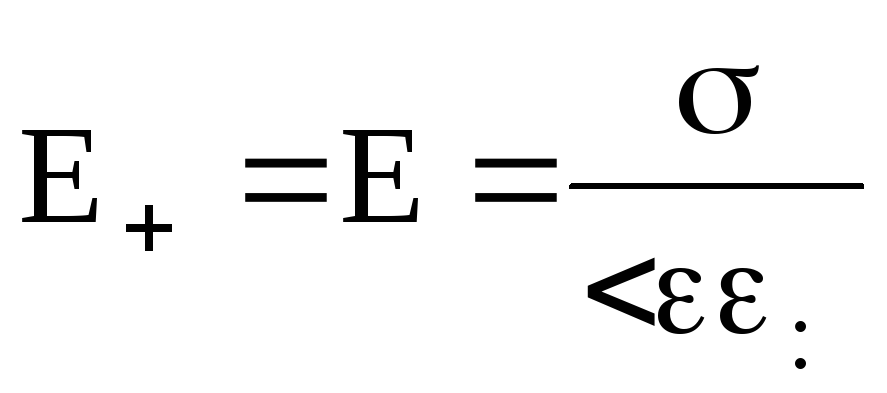 .
.
Jak widać z rys. 9, pola pomiędzy płaszczyznami sumują się ( linie energetyczne skierowane w jednym kierunku). Dlatego siła pola między płaszczyznami 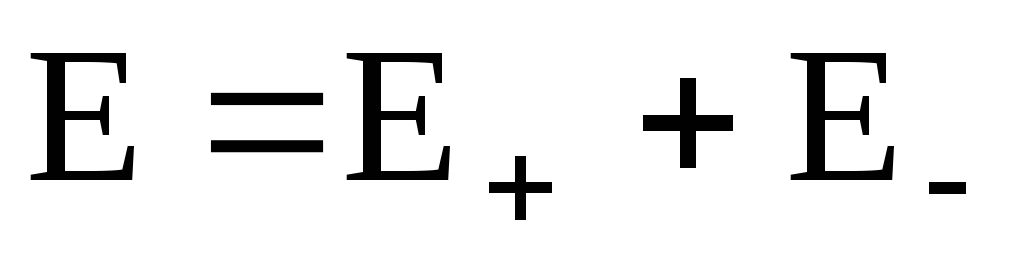 Lub
Lub
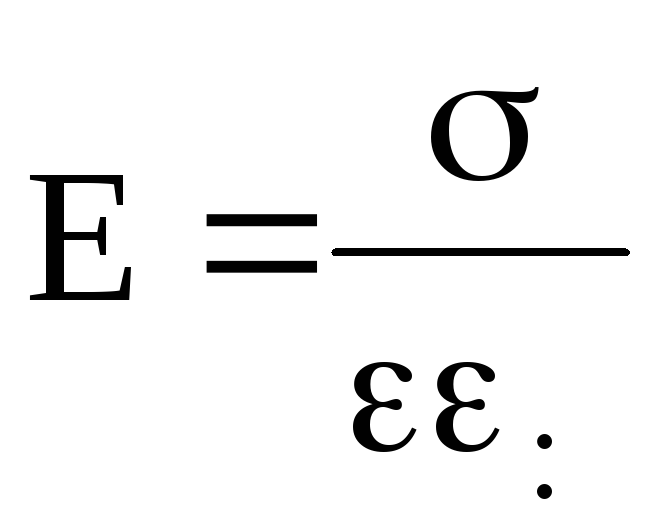 .
(14)
.
(14)
Po lewej i prawej stronie płaszczyzn odejmuje się pola (linie pola są skierowane ku sobie). Dlatego tutaj natężenie pola wynosi E = 0.
Projektując lampy elektronopromieniowe, kondensatory, soczewki elektronowe, fotopowielacze i inne urządzenia często konieczna jest znajomość kierunku wektora natężenia pola elektrostatycznego w dowolnym punkcie przestrzeni zamkniętej pomiędzy elektrodami złożony kształt. Analityczne obliczenie pola jest możliwe tylko przy najprostszych konfiguracjach elektrod. Dlatego złożone pola elektrostatyczne bada się eksperymentalnie (zwykle poprzez modelowanie pól elektrostatycznych w ośrodkach przewodzących).
Istota tej metody jest następująca. Produkowany jest układ elektrod, których kształt i względne położenie odwzorowują w określonej skali rzeczywiste urządzenie. Do elektrod przykładane jest napięcie. W takim przypadku powstaje między nimi pole elektrostatyczne.
Jeżeli przestrzeń pomiędzy elektrodami jest wypełniona ośrodkiem przewodzącym, wówczas prąd elektryczny. Pole elektrostatyczne zostanie zastąpione polem elektrycznym, które łatwiej jest zbadać eksperymentalnie.
Przy prądzie stałym zachodzi proces polaryzacji elektrolitycznej, zniekształcając pole. Aby tego uniknąć, stosuje się prąd przemienny o niskiej częstotliwości (I=50 Hz).
Konstrukcja powierzchni ekwipotencjalnych w polach o różnej konfiguracji w tej pracy odbywa się za pomocą instalacji pokazanej schematycznie na ryc. 7.
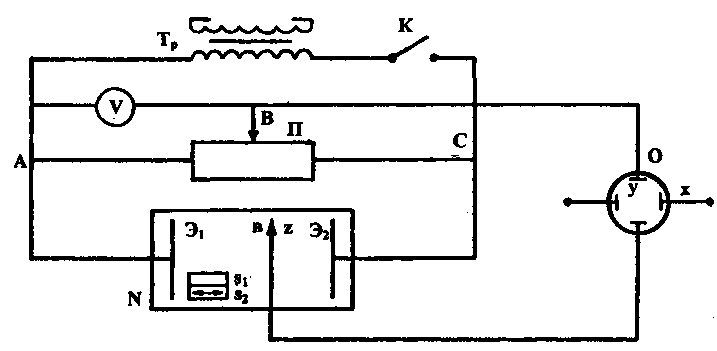
Zawiera łaźnię elektrolityczną N, woltomierz, potencjometr P, klucz K i elektrody E 1, mi 2 .
Porządek pracy
Elektrody metalowe E 1 i mi 2 , którego dziedzina jest badana. Elektrody mocowane są w uchwytach opierających się na ściankach wanny. Napięcie przemienne jest dostarczane do zacisków elektrod z transformatora T r.
Część pomiarową obwodu stanowi sonda Z (metalowy pręt z ostrym zakończeniem), potencjometr, oscyloskop i woltomierz.
Aby zbadać pole między elektrodami, umieszcza się w nim sondę, połączoną za pomocą oscyloskopu z punktem B potencjometru. Potencjał punktu B względem elektrody E 1 mierzy się woltomierzem V. Jeżeli między sondą Z a punktem B wystąpi różnica potencjałów, na ekranie oscyloskopu pojawi się sygnał sinusoidalny, którego amplituda jest proporcjonalna do potencjału różnica między nimi.
Poruszając sondą Z, można znaleźć w wannie punkt B, który ma taki sam potencjał jak punkt B. W tym przypadku amplituda sygnału na ekranie oscyloskopu będzie minimalna (nie ma możliwości osiągnięcia jego wartości zerowej, ponieważ podczas pomiaru prąd przemienny częstotliwość przemysłowa, zakłócenia w sprzęcie są nieuniknione). Po znalezieniu liczby punktów, których potencjał odpowiada potencjałowi punktu B, wyznaczana jest linia ekwipotencjalna.
Za pomocą uchwytów zamontuj w wannie dwie płaskie płyty równolegle do siebie. Na papierze milimetrowym w określonej skali (na przykład 1:2 lub 1:3) narysuj elektrody i zawarte między nimi dno wanny.
Zmontuj obwód elektryczny zgodnie ze schematem (rys. 7).
Włącz oscyloskop i rozgrzej go przez 1-2 minuty. W razie potrzeby użyj pokrętła ostrości, aby zmniejszyć świecącą linię na ekranie.
Włącz obwód.
Za pomocą potencjometru ustaw różnicę potencjałów pomiędzy punktami A i B: U AB = 0,1U.
Trzymając sondę pionowo, przesuń ją w obszarze S 1 jak pokazano (podwójna strzałka) na rys. 7, aż amplituda sygnału obserwowana na ekranie oscyloskopu będzie minimalna. Zaznacz znaleziony punkt linii ekwipotencjalnej na papierze milimetrowym. Znajdź co najmniej 7-8 punktów w wannie w różnych jej obszarach (a wzdłuż nich całą linię o równym potencjale) o φ 1 = 0,1U.
Powtórz pomiary dla φ 2 =0,3U, φ з =0,3U itd. Zbuduj co najmniej 6 linii ekwipotencjalnych.
Za pomocą potencjometru ustaw różnicę potencjałów pomiędzy punktami A i B na 0,5U.
W myślach zidentyfikuj w wannie linię ekwipotencjalną, której potencjały punktów wynoszą φ = 0,5U.
Pomiędzy płytki należy umieścić metalowy pierścień tak, aby jego średnica pokrywała się z zaznaczoną linią ekwipotencjalną.
Dowiedz się, czy potencjały punktów leżących wewnątrz pierścienia są takie same, czy też nie. Narysuj linie ekwipotencjalne na papierze milimetrowym, jeśli pomiędzy płaskimi elektrodami znajduje się pierścień z materiału przewodzącego, powtarzając operacje (patrz paragrafy 1,5,6).
Zamontuj nowe elektrody w wannie i powtórz czynności (patrz paragrafy 1,5,6).
Korzystając z danych pomiarowych z p. 5.6, wykreśl zależność potencjału φ x punktu pomiędzy elektrodami od odległości zmierzonej od elektrody E 1.
10.Dla pola wytwarzanego przez elektrody płaskie oblicz natężenie pola korzystając ze wzoru (9) dla czterech losowo wybranych punktów i narysuj linie siły.
11. Na wszystkich trzech wykresach skonstruowanych podczas wykonywania akapitów. 6,7,8, narysuj linie napięcia.
Pytania bezpieczeństwa
Jakie pole nazywa się elektrostatycznym?
Co to jest natężenie pola elektrostatycznego i w jakich jednostkach się je mierzy?
Jakie pole elektrostatyczne nazywa się jednorodnym?
Zdefiniuj powierzchnię potencjalną i ekwipotencjalną. Nazwij jednostki miary potencjału.
Jak zapisuje się i czyta twierdzenie Ostrogradskiego-Gaussa? Jaki jest jego cel?
Praca laboratoryjna nr 2
Dalekowschodni Uniwersytet Federalny
Szkoła Nauk
Podręcznik edukacyjno-metodyczny
DO praca laboratoryjna № 3.01
w dyscyplinie „warsztat fizyczny”
11200.62 – „fizyka”
Opracowany przez
Policzuk Witalij Efremowicz
Policzuk Raisa Fiodorowna
Władywostok
Wydawnictwo Dalekowschodnie uniwersytet federalny
BADANIE POLA ELEKTROSTATYCZNEGO
Wszystkie oddziaływania znane w fizyce – grawitacyjne, elektromagnetyczne, silne i słabe – mają charakter polowy. Pole fizyczne, obok materii, jest jednym z rodzajów materii. Pole elektryczne to rodzaj materii, poprzez którą oddziałują naładowane elektrycznie ciała. Ładunek ciał charakteryzuje się ilością ładunku na ciele i jest zwykle oznaczony literą q. Ilość fizyczna, przyjęty jako ilościowa miara ładunku ciał, oceniana na podstawie zdolności do oddziaływania elektrycznego, nazywa się ładunkiem.
W przyrodzie występują dwa rodzaje ładunków, potocznie zwane ładunkami dodatnimi i ujemnymi. Stabilna cząstka o najmniejszym ładunku ujemnym w postaci wolnej to elektron; odpowiednio ładunek dodatni – proton. Ładunki tych cząstek mają równy moduł z dokładnością 10 -22 (z tą dokładnością badano neutralność atomu), ale inne ich właściwości są różne (na przykład masa protonu m p jest większa od masy elektron m e 1836 razy).
Ładunki elektryczne charakteryzują się następującymi właściwościami:
Dyskretność (kwantyzacja) -Ładunek elektryczny dowolnego układu ciał składa się z całość liczba ładunków elementarnych stanowiąca wielokrotność ładunku elektronu lub protonu.
Addytywność ładunków elektrycznych – całkowity ładunek Q układu składającego się z N naładowanych cząstek jest równy sumie algebraicznej tych ładunków – Q= i.
Poddanie się prawu zachowania ładunków - algebraiczna suma ładunków elektrycznych ciał lub cząstek znajdujących się w odosobniony systemie, pozostaje wartością stałą, pomimo wszelkich wzajemnych konwersji w tym systemie.
Niezmienność - niezależność ładunku ciała od prędkości jego ruchu, tj. w dowolnym układzie odniesienia wielkość ładunku dane ciało jest taki sam.
Oddziaływanie ładunków elektrycznych q 1 i q 2 jest wynikiem działania pola elektrycznego ładunku q 1 na ładunek q 2 i odpowiednio pola elektrycznego ładunku q 2 na ładunek q 1 (w tym przypadku podobnie jak ładunki odpychają, a w odróżnieniu od ładunków przyciągają). Ładunek jest zawsze źródłem pola elektrycznego. Pole elektryczne wytworzone przez ładunek lub ładunki stacjonarne nazywa się elektrostatycznym. Pole elektrostatyczne – specjalny przypadek polu elektromagnetycznym i w idealnym przypadku istnieje tylko w układy inercyjne punkt odniesienia, w którym ładunki są nieruchome, gdyż każdy ruch ładunków elektrycznych powoduje pojawienie się pola magnetycznego.
Główne cechy pola elektrostatycznego (jak każdego innego) to napięcie i potencjał .
Siła pola elektrycznego mi w danym punkcie jest wielkością fizyczną równą sile F, za pomocą którego pole elektryczne oddziałuje na jednostkowy ładunek punktu probierczego q umieszczony w tym punkcie
(). Ładunek próbny to ładunek, którego pole własne nie zniekształca pola, w którym jest umieszczony. Napięcie jest wielkością wektorową i tak jest charakterystyka pola siłowego. Wektor napięcia mi ma kierunek zgodny z kierunkiem wektora siły działającej na ładunek dodatni w danym punkcie pola. Zgodnie z prawem Coulomba siła F interakcje pomiędzy nimi opłaty punktowe określone wzorem:
gdzie q 1 to ładunek tworzący pole, q to ładunek, na który oddziałuje pole wytworzone przez ładunek q 1, R jest wektorem łączącym źródło pola (ładunek q 1) ze współrzędną punktu pola, w którym znajduje się ładunek q. Następnie z prawa Coulomba wynika, że natężenie pola ładunku punktowego określa się według wzoru:
Opłata punktowa zwane ciałem naładowanym, którego wymiary można pominąć w porównaniu z wartością R. W układzie jednostek SI natężenie pola elektrycznego mierzy się w N/C lub V/m.
Pola elektryczne w ośrodkach liniowych (ośrodkach, w których nie ma ferroelektryków) są posłuszne zasada superpozycji pól - ich niezależne dodawanie: jeżeli w danym punkcie przestrzeni różne naładowane ciała tworzą niezależnie pola elektryczne o odpowiednio natężeniu E 1 , E 2 , .. En, a następnie wektor wynikowego natężenia pola elektrycznego mi równa sumie geometrycznej wektorów natężeń wszystkich pól elektrycznych, tj. E=E 1 +E 2 +...+En. Aby opisać pole elektryczne w wybranej przestrzeni, należy określić wektor natężenia w każdym punkcie pola. Zależność tę można przedstawić nie tylko analitycznie, ale także graficznie w postaci rodziny tzw. linii napięcia (linii pola ). Linia napięcia Pole elektryczne to linia, której styczna w każdym punkcie pokrywa się z wektorem natężenia pola w tym punkcie. Pole elektrostatyczne - pole źródłowe: jego linie siły (linie napięcia) nie mogą się przecinać; zaczynają się na ładunkach dodatnich, a kończą na ładunkach ujemnych, lub idą do nieskończoności od ładunków dodatnich i przechodzą od nieskończoności do ładunków ujemnych.
Linie pola rysowane są z taką częstotliwością, że liczba linii przecinających wyimaginowany obszar o powierzchni równej jedności i prostopadłych do linii pola jest równa wartości natężenia pola tego miejsca. i pola w danej lokalizacji. W rezultacie na podstawie gęstości linii pola elektrycznego można ocenić nie tylko kierunek, ale także wartość natężenia pola. Pole elektryczne, którego natężenie jest takie samo pod względem wielkości i kierunku w dowolnym punkcie przestrzeni, nazywa się jednorodnym.
Pole elektrostatyczne jest potencjalne- jest to pole, którego praca sił nie zależy od trajektorii ładunku, ale jest określona przez punkt początkowy i końcowy jego ruchu lub praca jego sił wzdłuż dowolnej zamkniętej trajektorii wynosi zero.
Jak wiadomo, pola potencjalne są ilościowo charakteryzowane przez energię potencjalną. Cechą energetyczną pola elektrostatycznego jest potencjał . Potencjał danego punktu pola to praca wykonana w celu przemieszczenia jednostkowego ładunku dodatniego (q=1) przez siły pola z nieskończoności do danego punktu pola. Ponieważ praca ma zawsze charakter względny (określa się, od którego punktu ciało się porusza), potencjał dowolnego punktu pola zależy od wyboru punktu odniesienia potencjału. Wybór potencjalnego punktu odniesienia nazywa się normalizacją potencjału. Potencjał można normalizować w dowolny sposób, ale najczęściej w fizyce normalizuje się go względem nieskończenie odległych od źródła pola punktów (ładunek q 1), przyjmując potencjał w tych punktach jako potencjał zerowy. W elektrotechnice potencjał Ziemi lub podłączonego do niej przewodnika przyjmuje się jako potencjał zerowy. Różnica potencjałów między dwoma punktami pola nazywana jest napięciem. Jednak różnica potencjałów i napięcie są sobie równe liczbowo tylko dla pól potencjalnych, do których zalicza się pole elektrostatyczne.
Napięcie i potencjał mierzone są w jednostkach SI w woltach (V). Potencjał 1 V ma punkt pola, do którego należy wykonać pracę 1 J, aby przenieść ładunek 1 C przez siły pola.
Zasada niezależnego dodawania pól (zasada superpozycji) pozwala obliczyć potencjał pola, generowane przez systemładunki q 1, q 2,…q n. Potencjał powstałego pola elektrostatycznego w danym punkcie, w odniesieniu do wybranej normalizacji, jest równy sumie algebraicznej potencjałów pola wytwarzanych przez każdy ładunek z osobna: j = j 1 +j 2 ×××+j n. Potencjał jest wielkością skalarną.
Wartość potencjału w każdym punkcie przestrzeni jest określona przez wielkość i konfigurację ładunku tworzącego pole, a także odległość od źródła pola do tego punktu. Na przykład potencjał pola wytworzony przez ładunek punktowy q w próżni względem nieskończoności jest określony przez wyrażenie:
gdzie ε ο jest stałą elektryczną próżni, r jest odległością od źródła pola ładunku q do punktu, w którym wyznacza się potencjał pola. Jeśli pole jest utworzone przez ładunek rozszerzony, wówczas potencjał j w tym miejscu określa bardziej złożony wzór:
gdzie ρ jest objętościową gęstością ładunku, V jest objętością naładowanego ciała.
Wyimaginowaną powierzchnię, na której wszystkie punkty mają ten sam potencjał, nazywamy powierzchnie o równym potencjale lub powierzchnie ekwipotencjalne. Korzystając z koncepcji powierzchni ekwipotencjalnej, możliwe jest graficzne przedstawienie pól elektrycznych w taki sam sposób, jak dzieje się to za pomocą linii sił. Przecinając się z płaszczyzną rysunku, dają powierzchnie ekwipotencjalne linie ekwipotencjalne .
Pracę pola powodującą przemieszczenie ładunku elektrycznego pomiędzy dwoma punktami pola określa wzór: A= q(j 1- j 2). Ze wzoru jasno wynika, że praca pola przemieszczająca ładunek wzdłuż powierzchni ekwipotencjalnej wynosi zero, ponieważ wszystkie punkty na powierzchni lub linii ekwipotencjalnej charakteryzują się tym samym potencjałem, a. oznacza to, że siła działająca na ładunek jest zawsze prostopadła do przemieszczenia. Z tego wnioskujemy, że:
1. L Linie naprężenia (linie pola) są zawsze prostopadłe (ortogonalne) do powierzchni ekwipotencjalnych (linii). 2. Powierzchnie ekwipotencjalne (linie) nie przecinają się.
Powierzchnie ekwipotencjalne można poprowadzić przez dowolny punkt pola, tj. Można narysować nieskończoną liczbę takich powierzchni. Dlatego zwyczajowo rysuje się powierzchnie ekwipotencjalne (linie) w taki sposób, aby różnica potencjałów dla dowolnych dwóch sąsiednich powierzchni była taka sama (j i +1 - j i) =const. W tym przypadku na podstawie gęstości powierzchni ekwipotencjalnych (linii) można jakościowo ocenić wielkość natężenia pola - im gęstsze są powierzchnie ekwipotencjalne, tym większe jest natężenie.
Natężenie i potencjał pola elektrostatycznego są ze sobą powiązane wzorem mi= - stopień. Z wzoru wynika, że w każdym punkcie pola wektor natężenia mi i potencjalny wektor gradientu j są równe pod względem wielkości i mają przeciwny kierunek.
Na rysunku 1 linie ciągłe przedstawiają linie ekwipotencjalne (krzywe ciągłe) i linie napięcia (krzywe przerywane) dla dwóch jednakowych przeciwnych ładunków – dipola.
Z własności ortogonalności linii pola i powierzchni ekwipotencjalnych wynika, że wzdłuż linii pola można znaleźć powierzchnię o równym potencjale. I odwrotnie, w oparciu o położenie powierzchni ekwipotencjalnych - konstrukcja linii pola. W niniejszej pracy wykorzystano tę drugą możliwość. . Wykorzystanie zależności pomiędzy napięciem a różnicą potencjałów mi =- gradφ, możesz znaleźć wielkość wektora natężenia w określonej części pola. Jeżeli Δφ jest różnicą potencjałów dwóch sąsiednich linii ekwipotencjalnych, a Δx jest odległością między nimi, mierzoną wzdłuż linii pola, to korzystając z przybliżonej zależności według wzoru E = możliwe jest w polu jednorodnym (lub nie- jednolite, ale w bardzo małej odległości), aby znaleźć wielkość wektora natężenia w polach powierzchniowych Δx.
 W pracy przeprowadzono jakościowe badanie pola elektrostatycznego, przedstawione graficznie za pomocą układu linii ekwipotencjalnych oraz układu prostopadłych do nich linii natężenia pola. Teoretycznie z reguły łatwiej jest obliczyć potencjały niż natężenia pola, ponieważ te pierwsze są wielkościami skalarnymi, a drugie wielkościami wektorowymi. Eksperymentalny pomiar potencjałów jest znacznie prostszy niż pomiar natężenia pola, ponieważ większość instrumentów używanych do badania pól mierzy różnice potencjałów, a nie natężenie pola. Dlatego w tej pracy laboratoryjnej eksperymentalnie określa się wartości potencjałów w różnych punktach pola, a nie siły. Linie pola badanych pól konstruowane są teoretycznie jako układ krzywych ortogonalnych do eksperymentalnie znalezionych powierzchni ekwipotencjalnych lub linii ekwipotencjalnych.
W pracy przeprowadzono jakościowe badanie pola elektrostatycznego, przedstawione graficznie za pomocą układu linii ekwipotencjalnych oraz układu prostopadłych do nich linii natężenia pola. Teoretycznie z reguły łatwiej jest obliczyć potencjały niż natężenia pola, ponieważ te pierwsze są wielkościami skalarnymi, a drugie wielkościami wektorowymi. Eksperymentalny pomiar potencjałów jest znacznie prostszy niż pomiar natężenia pola, ponieważ większość instrumentów używanych do badania pól mierzy różnice potencjałów, a nie natężenie pola. Dlatego w tej pracy laboratoryjnej eksperymentalnie określa się wartości potencjałów w różnych punktach pola, a nie siły. Linie pola badanych pól konstruowane są teoretycznie jako układ krzywych ortogonalnych do eksperymentalnie znalezionych powierzchni ekwipotencjalnych lub linii ekwipotencjalnych.
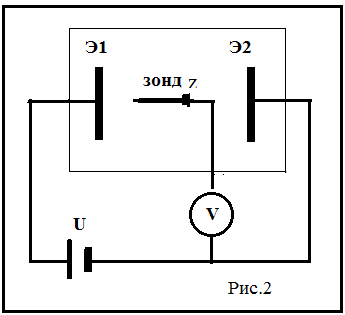
Do badania rozkładu potencjału w tej pracy wykorzystano metodę sondy. Jego istota polega na tym, że w badany punkt pola elektrycznego wprowadza się elektrodę - sonda . Sonda jest podłączona do urządzenia V, które mierzy wartość potencjału sondy w danym punkcie pola w stosunku do potencjału innego wybranego punktu pola, przyjętego jako wartość potencjału „zerowego”. W takim przypadku należy stworzyć takie warunki, aby sonda przyjęła potencjał punktu pola, w którym jest umieszczona. Tylko w tym przypadku wskazania przyrząd pomiarowy podłączony do sondy będzie odzwierciedlał prawidłowy obraz rozkładu potencjału w badanym polu. Spełnienie tego warunku w ośrodku nieprzewodzącym jest trudne, co doprowadziło do opracowania specjalnej metody badania pól elektrostatycznych poprzez sztuczne odtwarzanie ich struktury w ośrodkach przewodzących, przez które przepływa prąd stały. Dlatego od czasu studiów pole elektrostatyczne jest trudne do zrealizowania za pomocą sond, wówczas eksperymentalne badanie pola elektrostatycznego zastępuje się badaniem stałego w czasie prądu elektrycznego w ośrodkach słabo przewodzących. Metoda badania pola elektrostatycznego poprzez utworzenie innego, równoważnego mu pola nazywa się modelowanie.
W tej pracy ośrodek przewodzący jest słabym rozwiązaniem sól kuchenna, w którym zwilżana jest kartka papieru listowego. Elektrody metalowe (E1 i E2) o różnej konfiguracji są instalowane na kartce papieru i zasilane stałym napięciem ze źródła prądu U. Część pomiarowa instalacji obejmuje sondę i woltomierz cyfrowy V (multimetr) (ryc. 2).
Cel tej pracy:
1. Badania eksperymentalne pole elektrostatyczne w obszarze pomiędzy naładowanymi przewodnikami o różnych konfiguracjach i jego opis za pomocą linii ekwipotencjalnych i sił.
WYKONANIE PRACY:
1. Namocz kartkę papieru w roztworze soli kuchennej i połóż ją na płaskiej szkle.
2. Umieść płaskie elektrody na wilgotnym papierze. Zaznaczyć ołówkiem „wklej” położenie i kształt elektrod E na papierze.
3.Włącz zasilanie instalacji. Używanie woltomierza V sonda Zmierz potencjał każdej elektrody. Określ polaryzację elektrod. Zgodnie ze schematem (rys. 2) sonda Z na elektrodzie E2 wskaże wartość potencjału zerowego, przyjmowaną jako normalizacja (punkt odniesienia potencjału), a na elektrodzie E1 – wartość maksymalną, równą napięciu źródła prądu U. W konsekwencji , elektroda E2 ma biegunowość ujemną, a elektroda E1 - dodatnią .
4. Przesuwając sondę w pobliże elektrody o potencjale zerowym, za pomocą woltomierza znajdź na papierze co najmniej 10-15 punktów o potencjale 1,50 V względem zera. Zaznacz punkty na papierze ołówkiem i podpisz potencjalną wartość. Gładka krzywa przeprowadzona przez znalezione punkty da linię ekwipotencjalną o potencjale 1,5 V.
5. Wybierając „krok” zmiany potencjału ΔU = 0,5 V, powtórz pomiary z punktu 4 dla potencjałów 2; 2,5; 3; 3,5;4V ... do wartości potencjału na elektrodzie E 1.
6.Według wskazówek nauczyciela powtórz kroki 1-5 dla innych proponowanych układów elektrod symulujących pole ładunku punktowego, pole dipolowe, pole złożony systemładunek punktowy i samolot.
7.Po wyschnięciu kartek papieru połącz znajdujące się na nich punkty o równym potencjale liniami ekwipotencjalnymi. Skonstruuj obraz linii pola (ze wskazaniem ich kierunku) dla badanych par elektrod. Należy starać się rysować krzywe nie bezpośrednio przez punkty, ale tak, aby nie miały ostrych załamań i załamań.
8. W 4-5 punktach pola „płaskiego kondensatora” obliczyć ze wzoru E = wielkość wektora natężenia w przekroju pola Δx. We wzorze Δφ jest różnicą potencjałów dwóch sąsiednich linii ekwipotencjalnych, a Δx jest odległością między nimi, mierzoną wzdłuż linii pola.
1 .Siła oddziaływania dwóch ujemnych ładunków punktowych znajdujących się w pewnej odległości R od siebie, równi F. Znaki ładunków obu cząstek uległy odwróceniu. Tak, że siła interakcji F nie uległa zmianie, odległość pomiędzy ładunkami musi...
zmniejszyć 2 razy
pozostawić bez zmian
zwiększyć 4 razy
zmniejszyć o
zwiększyć 2 razy
Rozwiązanie:
Pozostaw bez zmian
2.
Rysunek pokazuje kierunek wektora natężenia powstałego pola elektrycznego ładunków punktowych q 1 i q 2 w punkcie A. 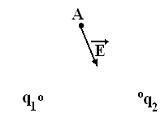
Jednocześnie relacja obowiązuje dla opłat...
, ; , ; , ; ,
Rozwiązanie:
Zbuduj wszystkie opcje. , - Tak.
3.
Pole elektrostatyczne tworzą dwa ładunki punktowe: i . Stosunek potencjału pola wytworzonego przez drugi ładunek w punkcie A do potencjału powstałego pola w tym punkcie wynosi… 4 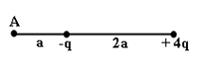
Rozwiązanie:
(Współczynniki podziału są zmniejszone)
4.
Pole elektrostatyczne tworzone jest przez układ ładunków punktowych. 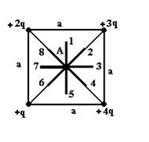
Wektor natężenia pola w punkcie A jest zorientowany w kierunku ...7
Rozwiązanie:
![]() – wektory natężenia pola utworzone przez ładunki punktowe Wykonaj rysunek.
– wektory natężenia pola utworzone przez ładunki punktowe Wykonaj rysunek.
5 . Pole elektrostatyczne jest tworzone przez układ ładunków punktowych i.
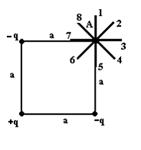
Gradient potencjału pola w punkcie A jest zorientowany w kierunku ...2
Rozwiązanie:
Przekątna jest równa . Napięcie z ładunków jest kierowane do punktu A wzdłuż 6 i ma taką samą wielkość. Napięcie z ładunku w punkcie A jest skierowane wzdłuż 2 i ma taką samą wielkość. Ponieważ 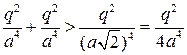 , wówczas napięcie w punkcie A jest skierowane wzdłuż 6. Zatem wzdłuż 2. ( dla uproszczenia współczynniki pominięto)
, wówczas napięcie w punkcie A jest skierowane wzdłuż 6. Zatem wzdłuż 2. ( dla uproszczenia współczynniki pominięto)
6
.Wektor natężenia pola elektrostatycznego w punkcie A pomiędzy powierzchniami ekwipotencjalnymi B i B ma kierunek ... 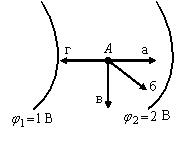
Rozwiązanie:
Ponieważ wektor, potem wektor Zawsze skierowany w stronę spadku prostopadle do powierzchni ekwipotencjalnych, tj. ku G.
7
. Pole elektrostatyczne tworzone jest przez układ ładunków punktowych. 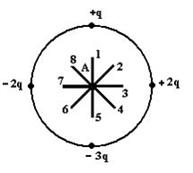
Wektor natężenia pola w punkcie A jest zorientowany w kierunku ...6
Rozwiązanie:
Zgodnie z zasadą superpozycji pola natężenie w punkcie A jest równe: , gdzie ![]() są wektorami natężenia pola utworzonego przez ładunki punktowe , , , odpowiednio w rozważanym punkcie. Rysunek pokazuje kierunki tych wektorów.
są wektorami natężenia pola utworzonego przez ładunki punktowe , , , odpowiednio w rozważanym punkcie. Rysunek pokazuje kierunki tych wektorów. 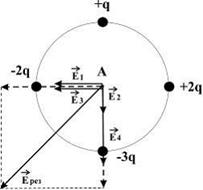
. Biorąc pod uwagę wielkość ładunków oraz fakt, że punkt A jest jednakowo oddalony od każdego ładunku, możemy stwierdzić, że tworzy on przekątną kwadratu o boku 2E 1. Zatem wektor natężenia pola w punkcie A jest zorientowany w kierunku 6.
8
. W pewnym obszarze przestrzeni wytworzyło się pole elektrostatyczne, którego potencjał opisuje funkcja . Wektor natężenia pola elektrycznego w punkcie przestrzeni pokazanym na rysunku będzie miał kierunek ... 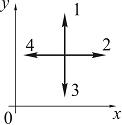 Rozwiązanie:
Rozwiązanie:![]() , , , . Stąd
, , , . Stąd ![]() , tj. wektor napięcia jest skierowany wzdłuż 4.
, tj. wektor napięcia jest skierowany wzdłuż 4.
9
. Pole elektrostatyczne tworzą dwie równoległe, nieskończone płaszczyzny naładowane przeciwstawnymi ładunkami o tej samej gęstości ładunku powierzchniowego. Odległość między płaszczyznami wynosi D.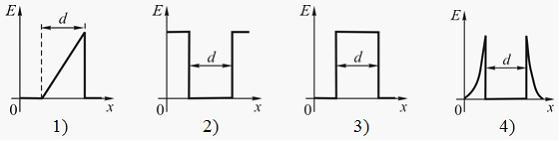
Rozkład napięć mi takie pole wzdłuż osi X, prostopadle do płaszczyzn, poprawnie pokazane na rysunku...
Rozwiązanie:
Pole elektrostatyczne jest w tym przypadku skoncentrowane pomiędzy płaszczyznami i jest jednorodne. Natężenie pola jest stałe i nie zależy od x, a na zewnątrz jest równe zero. Zatem prawidłowy wykres przedstawiono na rysunku 3.
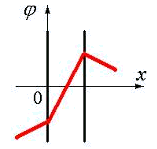
10.
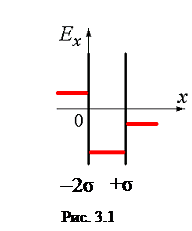 Pole elektryczne tworzą dwie równoległe płaszczyzny naładowane gęstościami powierzchniowymi –
2σ i +σ. Na ryc. 3.1 pokazuje jakościową zależność rzutu naprężenia Były ze współrzędnych X na zewnątrz płyt i pomiędzy płytami. Wykres poprawnie oddaje charakter zmiany potencjału φ tego pola
Pole elektryczne tworzą dwie równoległe płaszczyzny naładowane gęstościami powierzchniowymi –
2σ i +σ. Na ryc. 3.1 pokazuje jakościową zależność rzutu naprężenia Były ze współrzędnych X na zewnątrz płyt i pomiędzy płytami. Wykres poprawnie oddaje charakter zmiany potencjału φ tego pola
| 1) na ryc. 3.2 | 2) na ryc. 3.3 |
| 3) na ryc. 3.4 | 4) na ryc. 3.5 |
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
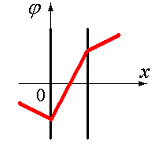 Ryż. 3.4 |
|
TEORIA POLA
Teoria pola to badanie zjawisk elektrycznych i magnetycznych, zasad teoretycznych i praw, którym podlegają te zjawiska, oraz wynikających z nich metod obliczeniowych.
Pole elektromagnetyczne jest szczególnym rodzajem materii, jest nośnikiem energii i posiada specyficzne (wrodzone tylko jemu) właściwości elektryczne i magnetyczne. Przedstawimy podstawowe właściwości i metody obliczania pól w kolejności przejścia od prostszych do bardziej złożonych. Zgodnie z tym najpierw rozważymy pola stałe w czasie, a dopiero potem zbadamy zmienne pole elektromagnetyczne. Badanie wszystkich typów pól poszerza pojęcia fizyczne pola, znane na lekcjach fizyki, przyczynia się do głębszego zrozumienia procesów zachodzących w urządzeniach elektrycznych, jest ważne z praktycznego punktu widzenia, ponieważ pozwala rozwiązać wiele problemów o istotnym znaczeniu nie tylko dla teorii obwody elektryczne, ale także problemy bardziej ogólne (promieniowanie i kanalizowanie energii elektrycznej itp.).
Badać będziemy jedynie pola w ośrodkach jednorodnych (identycznych we wszystkich punktach pola) i izotropowych (o właściwościach niezależnych od natężenia pola).
Pole elektrostatyczne
Pole elektrostatyczne jest szczególnym przypadkiem pola elektromagnetycznego; jest ono tworzone przez ładunki, które są nieruchome w przestrzeni (w stosunku do obserwatora) i stałe w czasie. Pole elektrostatyczne nie oddziałuje bezpośrednio na narządy zmysłów człowieka, ma jednak wrodzoną zdolność oddziaływania siłą mechaniczną na umieszczony w nim ładunek testowy. Efekt ten jest podstawą do detekcji pola elektrostatycznego i określenia jego natężenia.
Głównymi wielkościami charakteryzującymi właściwości tego pola są jego natężenie i potencjał. Jeśli ładunek próbny zostanie umieszczony w polu elektrostatycznym na tyle małym, że jego obecność nie zniekształci go, wówczas zadziała na niego siła. Stosunek tej siły do wielkości ładunku określi natężenie pola 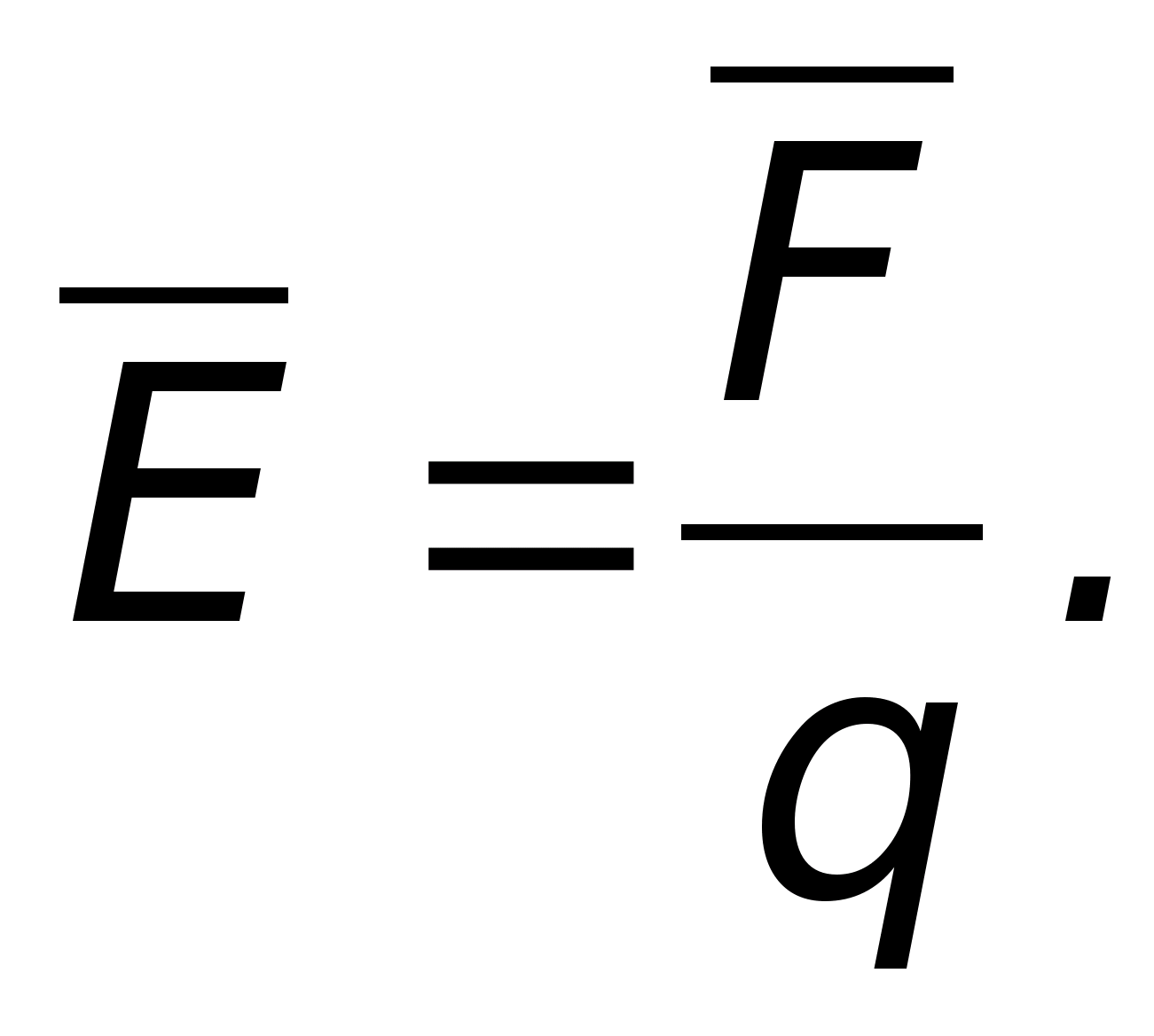 Jeśli
Jeśli 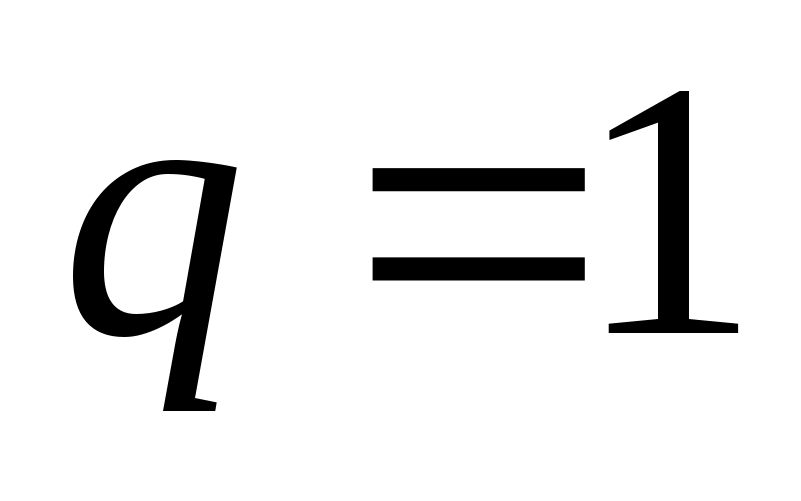 , To
, To  Wynika z tego, że natężenie pola jest równe sile działającej na jednostkowy ładunek dodatni i charakteryzuje natężenie pola; Jednostka napinająca
Wynika z tego, że natężenie pola jest równe sile działającej na jednostkowy ładunek dodatni i charakteryzuje natężenie pola; Jednostka napinająca
D  Pomińmy, że w pewnym polu elektrostatycznym pojedynczy dodatni ładunek próbny pod wpływem sił pola przemieszcza się z punktu 1 do punktu 2 (rys. 11.1). Następnie
Pomińmy, że w pewnym polu elektrostatycznym pojedynczy dodatni ładunek próbny pod wpływem sił pola przemieszcza się z punktu 1 do punktu 2 (rys. 11.1). Następnie  wykona pracę, aby przenieść ten ładunek z punktu 1 do punktu 2. Z kursu fizyki wiadomo, że praca wykonana podczas przemieszczania jednostkowego ładunku dodatniego z jednego punktu do drugiego to napięcie lub różnica potencjałów, tj.
wykona pracę, aby przenieść ten ładunek z punktu 1 do punktu 2. Z kursu fizyki wiadomo, że praca wykonana podczas przemieszczania jednostkowego ładunku dodatniego z jednego punktu do drugiego to napięcie lub różnica potencjałów, tj. 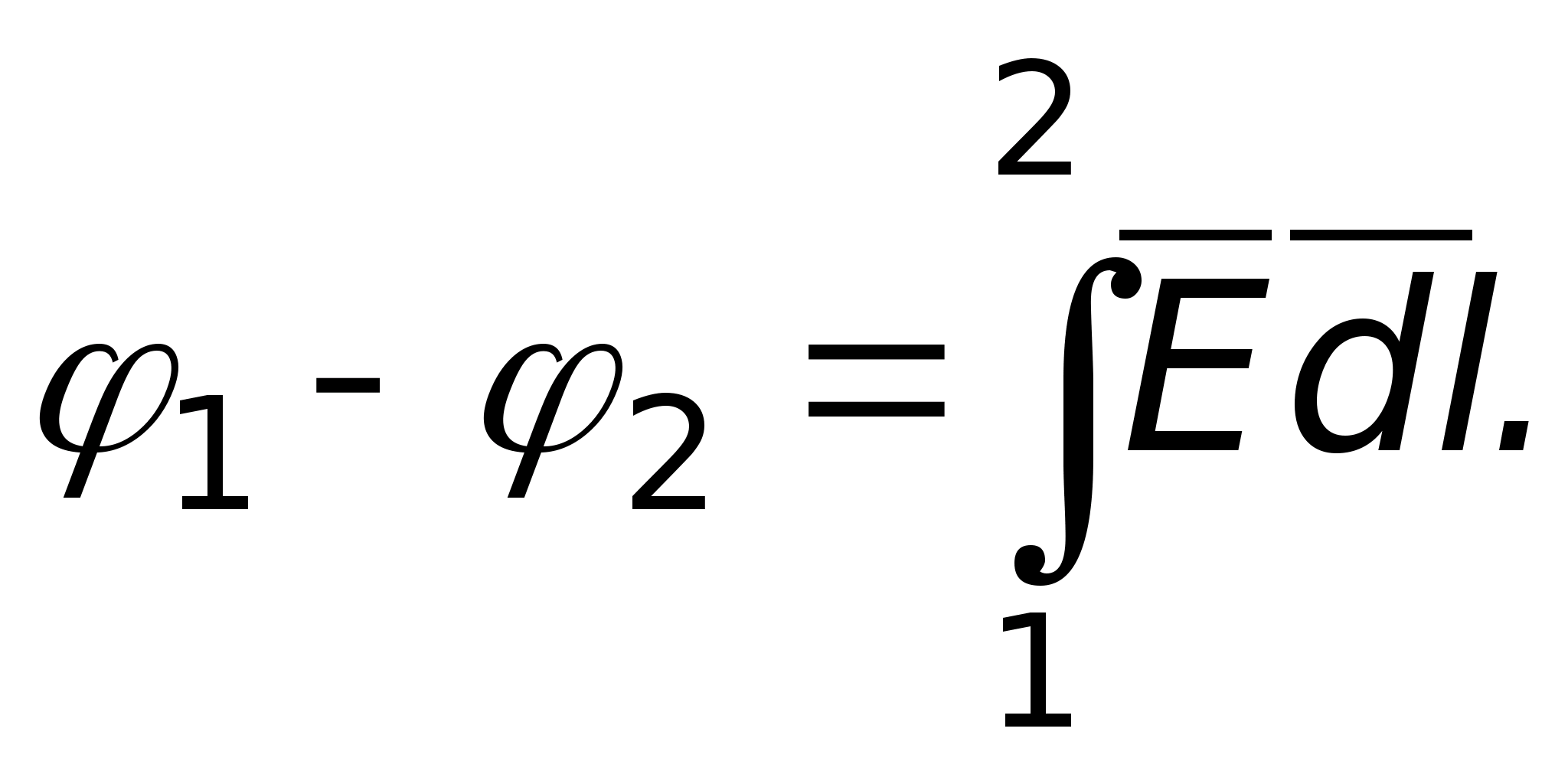 Jeśli
Jeśli 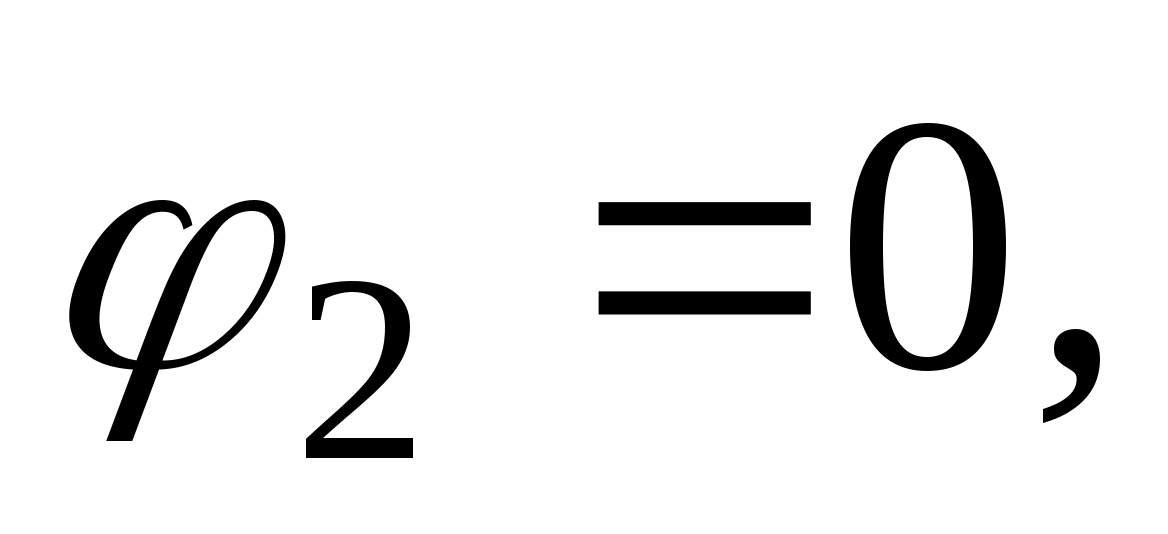 To
To 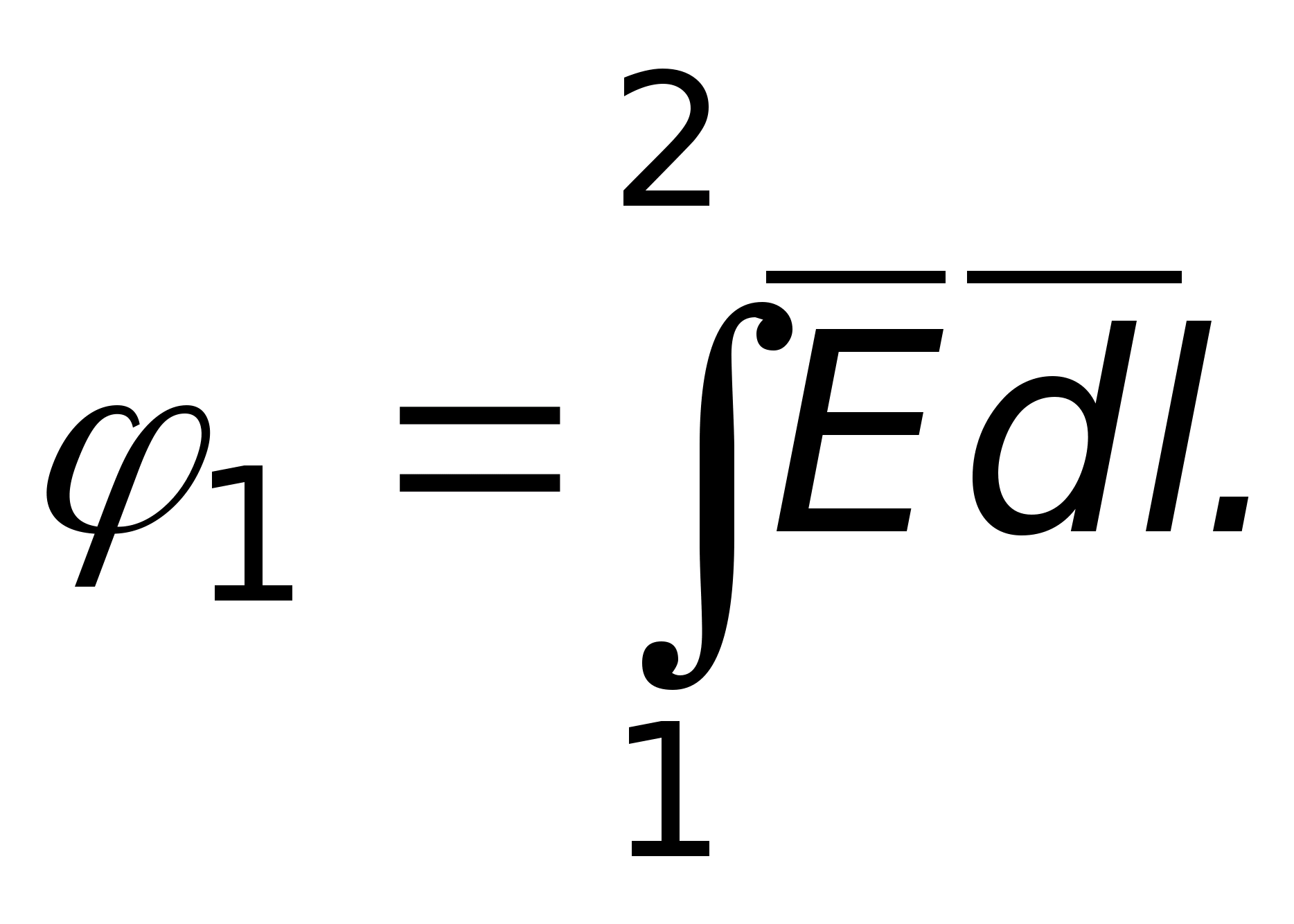 Wynika z tego, że potencjał pewnego punktu to praca wykonana w celu przeniesienia jednostkowego ładunku dodatniego z danego punktu do takiego, którego potencjał wynosi zero. Jako punkt o potencjale zerowym można wybrać dowolny punkt. Często umieszcza się go w nieskończoności, czasem na powierzchni ziemi. Jeśli zostanie wybrany punkt o potencjale zerowym, wówczas potencjały wszystkich pozostałych punktów zostaną całkowicie jednoznacznie określone. Z tego, co zostało rozważone, jasno wynika, że potencjał jest określany z dokładnością do stałej, w zależności od tego, gdzie znajduje się punkt o potencjale zerowym. Pod tym względem związek między potencjałem a napięciem jest zapisany w następujący sposób:
Wynika z tego, że potencjał pewnego punktu to praca wykonana w celu przeniesienia jednostkowego ładunku dodatniego z danego punktu do takiego, którego potencjał wynosi zero. Jako punkt o potencjale zerowym można wybrać dowolny punkt. Często umieszcza się go w nieskończoności, czasem na powierzchni ziemi. Jeśli zostanie wybrany punkt o potencjale zerowym, wówczas potencjały wszystkich pozostałych punktów zostaną całkowicie jednoznacznie określone. Z tego, co zostało rozważone, jasno wynika, że potencjał jest określany z dokładnością do stałej, w zależności od tego, gdzie znajduje się punkt o potencjale zerowym. Pod tym względem związek między potencjałem a napięciem jest zapisany w następujący sposób: 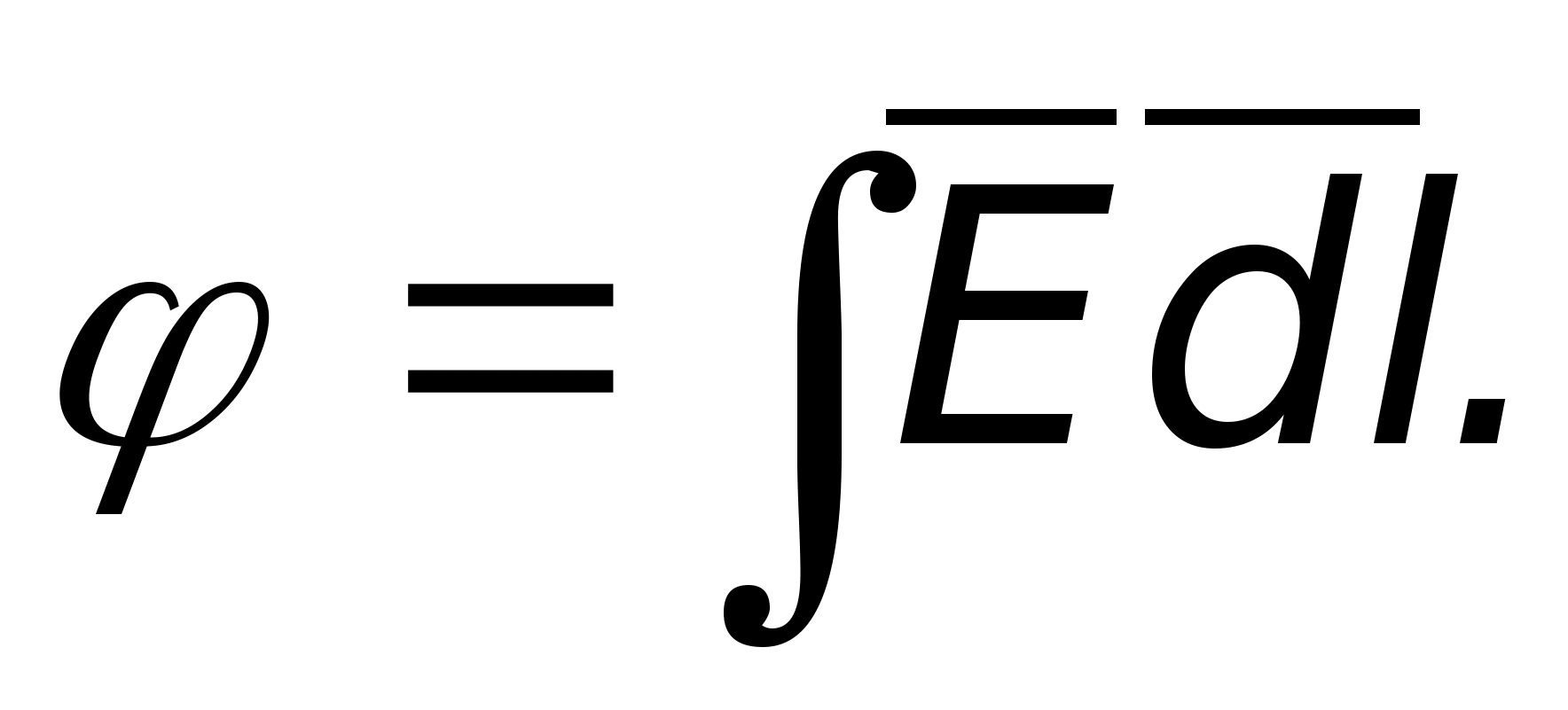 Fakt, że potencjał jest wyznaczany z dokładnością do stałej, nie ma praktycznego znaczenia, ponieważ Ważne jest napięcie, które jest równe różnicy potencjałów, a po jego przyjęciu stała całkowania ulega zniszczeniu.
Fakt, że potencjał jest wyznaczany z dokładnością do stałej, nie ma praktycznego znaczenia, ponieważ Ważne jest napięcie, które jest równe różnicy potencjałów, a po jego przyjęciu stała całkowania ulega zniszczeniu.
Jeśli  weź wzdłuż zamkniętego konturu, to da zero, tj.
weź wzdłuż zamkniętego konturu, to da zero, tj.  Oznacza to, że podczas poruszania się po zamkniętym konturze pewna ilość pracy jest wykonywana przez siły pola i dokładnie taka sama praca jest wykonywana przeciwko siłom pola. Stosunek
Oznacza to, że podczas poruszania się po zamkniętym konturze pewna ilość pracy jest wykonywana przez siły pola i dokładnie taka sama praca jest wykonywana przeciwko siłom pola. Stosunek  wyraża jedną z głównych właściwości pola elektrostatycznego - jest nim potencjał (potencjalne są wszystkie pola, dla których zachodzi podobna zależność - grawitacyjne, termiczne itp.).
wyraża jedną z głównych właściwości pola elektrostatycznego - jest nim potencjał (potencjalne są wszystkie pola, dla których zachodzi podobna zależność - grawitacyjne, termiczne itp.).
Graficzny obraz pola elektrostatycznego
Pole elektrostatyczne wyznacza się, jeśli znane jest prawo zmiany natężenia i potencjału w funkcji współrzędnych. Można go wyraźniej scharakteryzować za pomocą układu sił i linii ekwipotencjalnych, co nazywa się jego obrazem graficznym. Linia sił to linia narysowana w pamięci w polu, która zaczyna się na ciele naładowanym dodatnio, a kończy na ciele naładowanym ujemnie, a styczna do której w dowolnym punkcie wyznacza kierunek wektora mi. Bardzo mały ładunek dodatni poruszałby się wzdłuż linii siły, mając zdolność swobodnego poruszania się i nie mając bezwładności. Ponieważ ładunki dodatnie i ujemne nie mogą znajdować się w tym samym punkcie, linie siły mają początek i koniec, nie mogą się one zamykać. W dowolnym polu elektrostatycznym powierzchnie ekwipotencjalne można narysować jako zbiory punktów o tym samym potencjale. Jeśli pole zostanie przecięte dowolną płaszczyzną, to w powstałym przekroju widoczne będą ślady powierzchni ekwipotencjalnych, które nazywane są liniami ekwipotencjalnymi. W przeciwieństwie do linii sił, linie ekwipotencjalne są ciągłe, zamknięte w sobie. W dowolnym punkcie pola siła i linie ekwipotencjalne są do siebie prostopadłe. Jako przykład podajemy graficzny obraz pola elektrostatycznego dwóch ładunków punktowych (ryc. 11.2).
Czwiązek pomiędzy natężeniem pola a potencjałem
Wyjaśniona wcześniej zależność pomiędzy napięciem a potencjałem  nazywana całką. W praktyce częściej stosuje się zależność różnicową między tymi wielkościami. Aby to wyjaśnić, zidentyfikujmy dwie linie ekwipotencjalne w pewnym polu elektrostatycznym (ryc. 11.3). Niech wszystkie punkty pierwszej linii mają potencjał φ
1, a drugi – φ
2. Dla pewności założymy to φ
1 >φ
2, ale różnią się one w nieskończenie małej ilości, tj. φ
1 -φ
2 =Dφ
. Odległość między liniami – dł. Wybierzmy dowolny punkt 1 na pierwszej linii i punkt 2 na drugiej, jeśli różnicę potencjałów między tymi punktami podzielimy przez najkrótszą odległość między nimi (w linii prostej).
nazywana całką. W praktyce częściej stosuje się zależność różnicową między tymi wielkościami. Aby to wyjaśnić, zidentyfikujmy dwie linie ekwipotencjalne w pewnym polu elektrostatycznym (ryc. 11.3). Niech wszystkie punkty pierwszej linii mają potencjał φ
1, a drugi – φ
2. Dla pewności założymy to φ
1 >φ
2, ale różnią się one w nieskończenie małej ilości, tj. φ
1 -φ
2 =Dφ
. Odległość między liniami – dł. Wybierzmy dowolny punkt 1 na pierwszej linii i punkt 2 na drugiej, jeśli różnicę potencjałów między tymi punktami podzielimy przez najkrótszą odległość między nimi (w linii prostej).  uzyskana wartość będzie charakteryzowała szybkość zmiany potencjału w kierunku najkrótszej odległości między punktami. Prędkość ta zależy od sposobu wybierania punktów. Jeśli np. punkt 2 zostanie przesunięty w górę, to spadnie, bo tak nie jest Dφ
ulegnie zmianie, a odległość między punktami wzrośnie. Jeśli punkt 2 zostanie przesunięty w dół, wskazywana prędkość wzrasta. Kiedy punkt 2 zajmie pozycję najbliższą punktowi 1 (punkt 3), tempo potencjalnej zmiany osiągnie maksimum. W matematyce pojęcie gradientu funkcji skalarnej wprowadza się jako szybkość jej zmian, przyjmowaną w kierunku największego wzrostu. Zastosujmy to pojęcie do potencjału, tj. rozważać absolwentφ
. Będzie to wektor - ma kierunek od punktu 3 do punktu 1 (kierunek największego wzrostu), a jego moduł jest równy
uzyskana wartość będzie charakteryzowała szybkość zmiany potencjału w kierunku najkrótszej odległości między punktami. Prędkość ta zależy od sposobu wybierania punktów. Jeśli np. punkt 2 zostanie przesunięty w górę, to spadnie, bo tak nie jest Dφ
ulegnie zmianie, a odległość między punktami wzrośnie. Jeśli punkt 2 zostanie przesunięty w dół, wskazywana prędkość wzrasta. Kiedy punkt 2 zajmie pozycję najbliższą punktowi 1 (punkt 3), tempo potencjalnej zmiany osiągnie maksimum. W matematyce pojęcie gradientu funkcji skalarnej wprowadza się jako szybkość jej zmian, przyjmowaną w kierunku największego wzrostu. Zastosujmy to pojęcie do potencjału, tj. rozważać absolwentφ
. Będzie to wektor - ma kierunek od punktu 3 do punktu 1 (kierunek największego wzrostu), a jego moduł jest równy 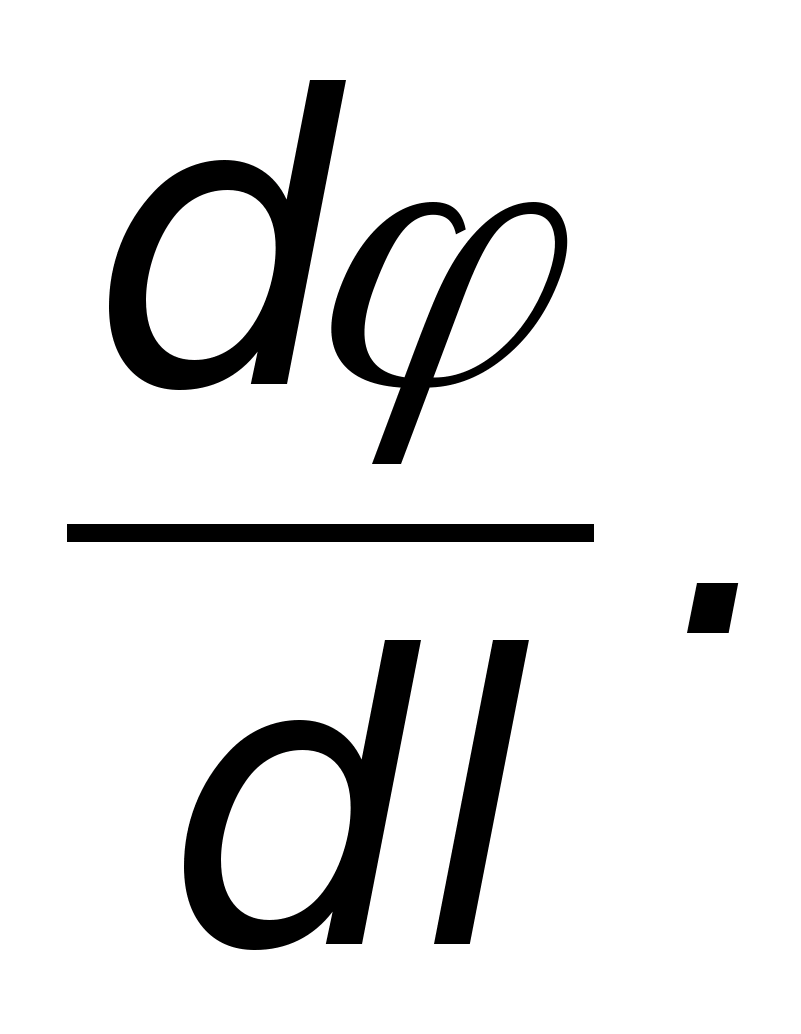 Siła pola jest skierowana
z wyższego potencjału ( φ
1) do mniejszego ( φ
2), a jego moduł jest równy
Siła pola jest skierowana
z wyższego potencjału ( φ
1) do mniejszego ( φ
2), a jego moduł jest równy 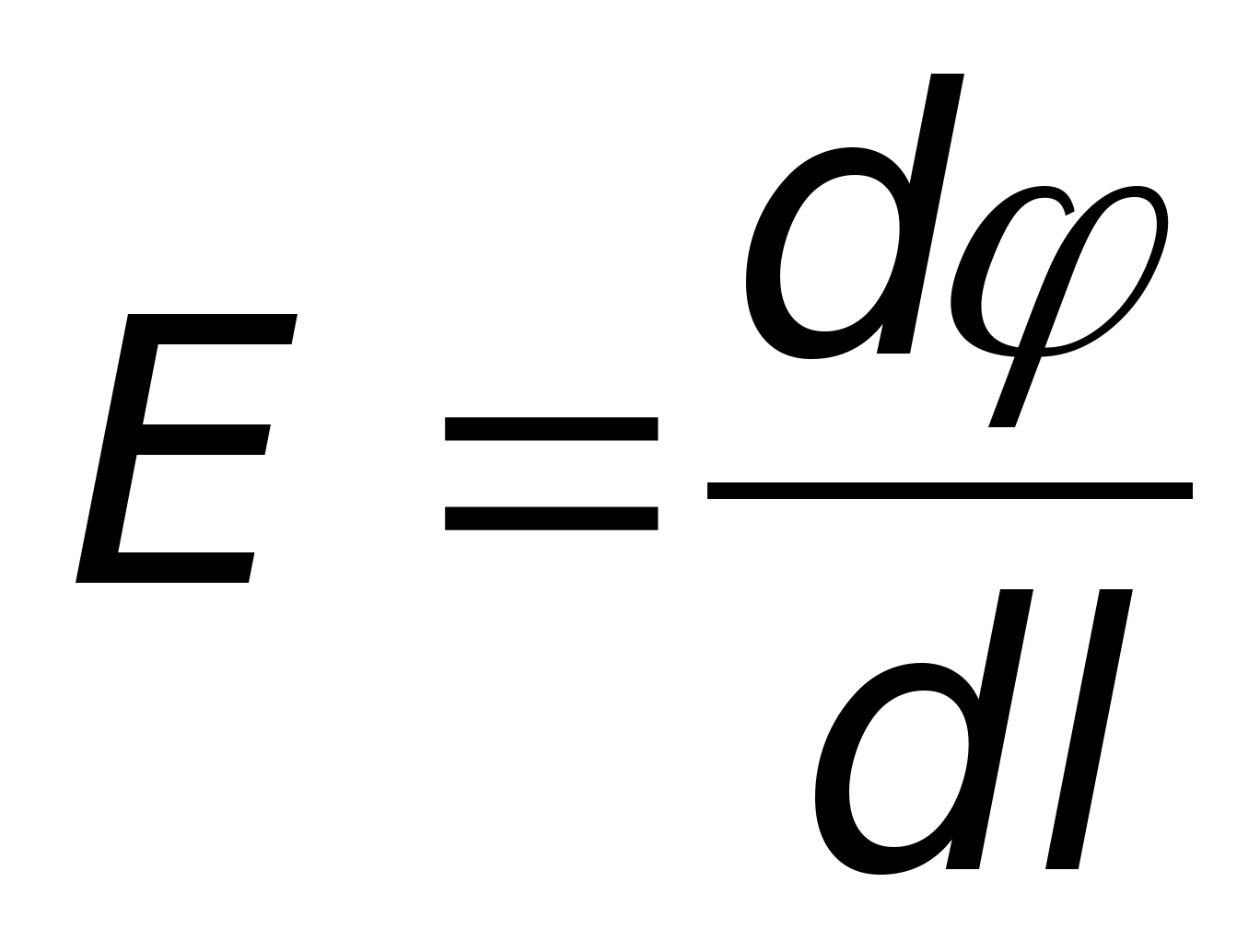 (patrz formularz integralny). Ponieważ moduły wektorów mi i gradφ są takie same, ale są zatem skierowane w przeciwne strony
(patrz formularz integralny). Ponieważ moduły wektorów mi i gradφ są takie same, ale są zatem skierowane w przeciwne strony 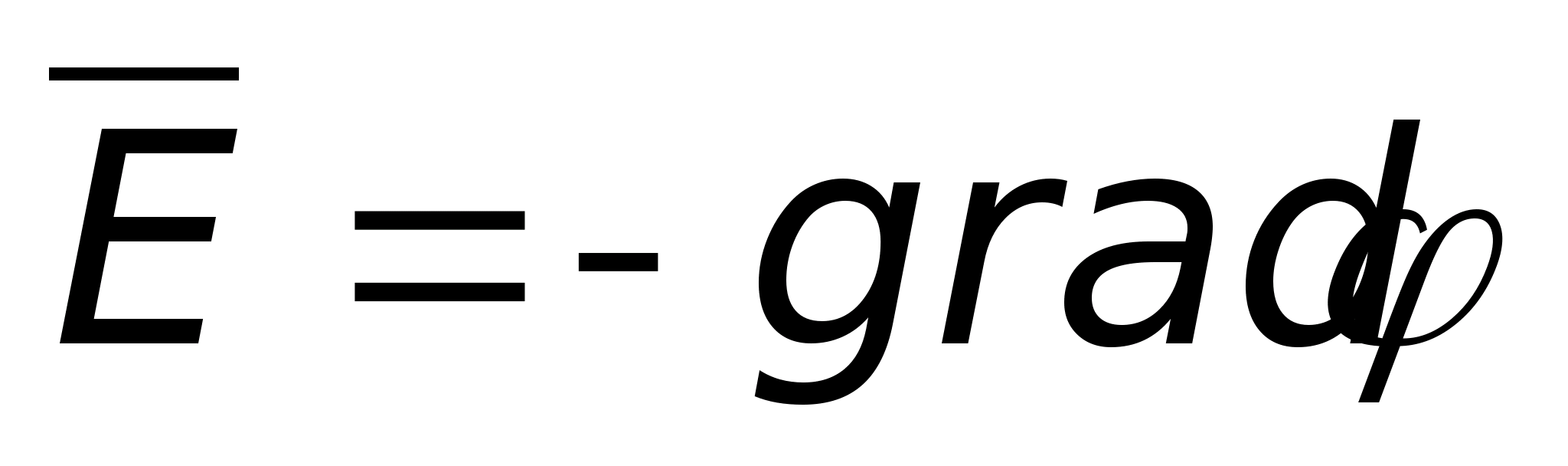 .
.
Kierunek największego wzrostu potencjału w ogólnym przypadku nie pokrywa się zatem z żadną osią współrzędnych absolwentφ
jest przedstawiany jako suma rzutów wzdłuż osi współrzędnych, na przykład w prostokątnym układzie współrzędnych (ryc. 11.4) 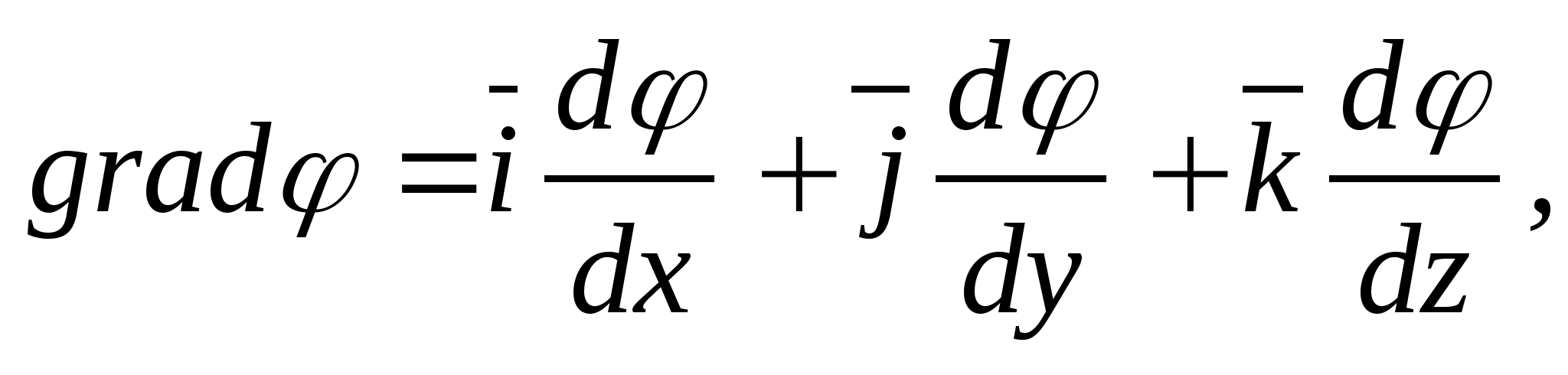 Gdzie
Gdzie  - wektory (wektory jednostkowe) układu prostokątnego,
- wektory (wektory jednostkowe) układu prostokątnego,  - szybkość zmian potencjału wzdłuż odpowiedniej osi. Napięcie mi można również zapisać za pomocą projekcji
- szybkość zmian potencjału wzdłuż odpowiedniej osi. Napięcie mi można również zapisać za pomocą projekcji  Dwa wektory są sobie równe, jeśli mają te same rzuty, tj.
Dwa wektory są sobie równe, jeśli mają te same rzuty, tj. 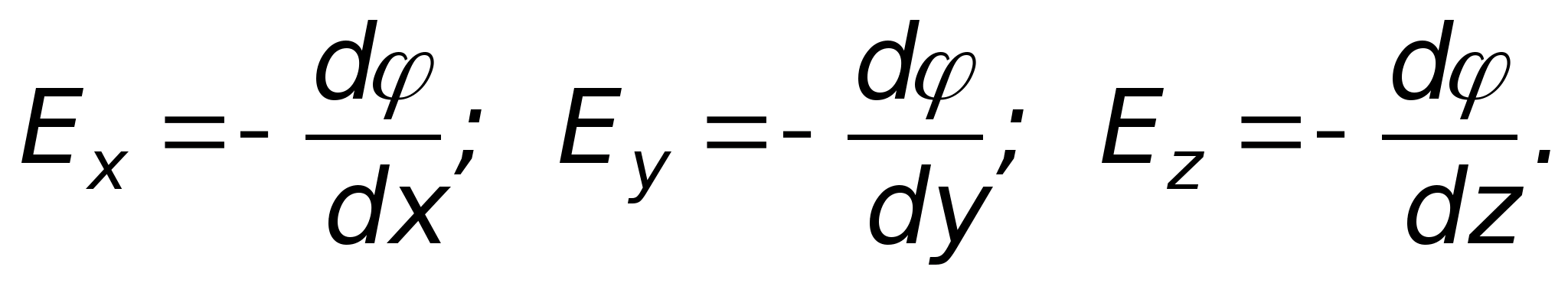 W obliczeniach praktycznych wykorzystywane są trzy ostatnie wzory.
W obliczeniach praktycznych wykorzystywane są trzy ostatnie wzory.
Aby skrócić zapis różnych operacji w teorii pola, powszechnie stosuje się operator różniczkowy Hamiltona (nabla), który nie ma fizycznego znaczenia, rozumiany jako suma pochodnych cząstkowych wzdłuż osi współrzędnych pomnożona przez odpowiednie wektory jednostkowe. W kartezjańskim układzie współrzędnych ma on postać: 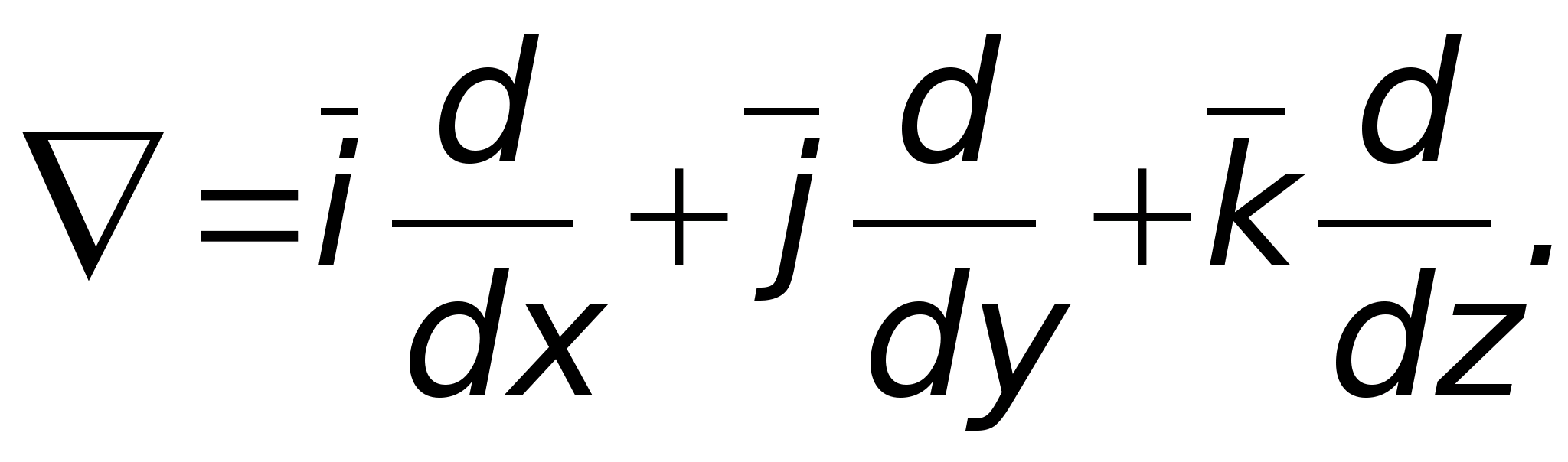 Formalnie nabla można uznać za wektor. Można go zastosować zarówno do funkcji skalarnych, jak i wektorowych. Funkcja, na podstawie której wykonywana jest akcja (różniczkowanie wzdłuż osi współrzędnych lub różniczkowanie przestrzenne), jest zapisywana po prawej stronie
Formalnie nabla można uznać za wektor. Można go zastosować zarówno do funkcji skalarnych, jak i wektorowych. Funkcja, na podstawie której wykonywana jest akcja (różniczkowanie wzdłuż osi współrzędnych lub różniczkowanie przestrzenne), jest zapisywana po prawej stronie  Jeśli po prawej stronie
Jeśli po prawej stronie  Jeśli funkcja nie jest określona, wówczas sam operator nabla nie jest używany (podobnie jak sin, log itp.). Zastosowanie operatora nabla do potencjału
Jeśli funkcja nie jest określona, wówczas sam operator nabla nie jest używany (podobnie jak sin, log itp.). Zastosowanie operatora nabla do potencjału  i porównując to z
i porównując to z  , widzimy, że =
, widzimy, że =  (dla funkcji skalarnej pochodne cząstkowe i całkowite są takie same). Wówczas związek pomiędzy napięciem a potencjałem można zapisać następująco:
(dla funkcji skalarnej pochodne cząstkowe i całkowite są takie same). Wówczas związek pomiędzy napięciem a potencjałem można zapisać następująco: 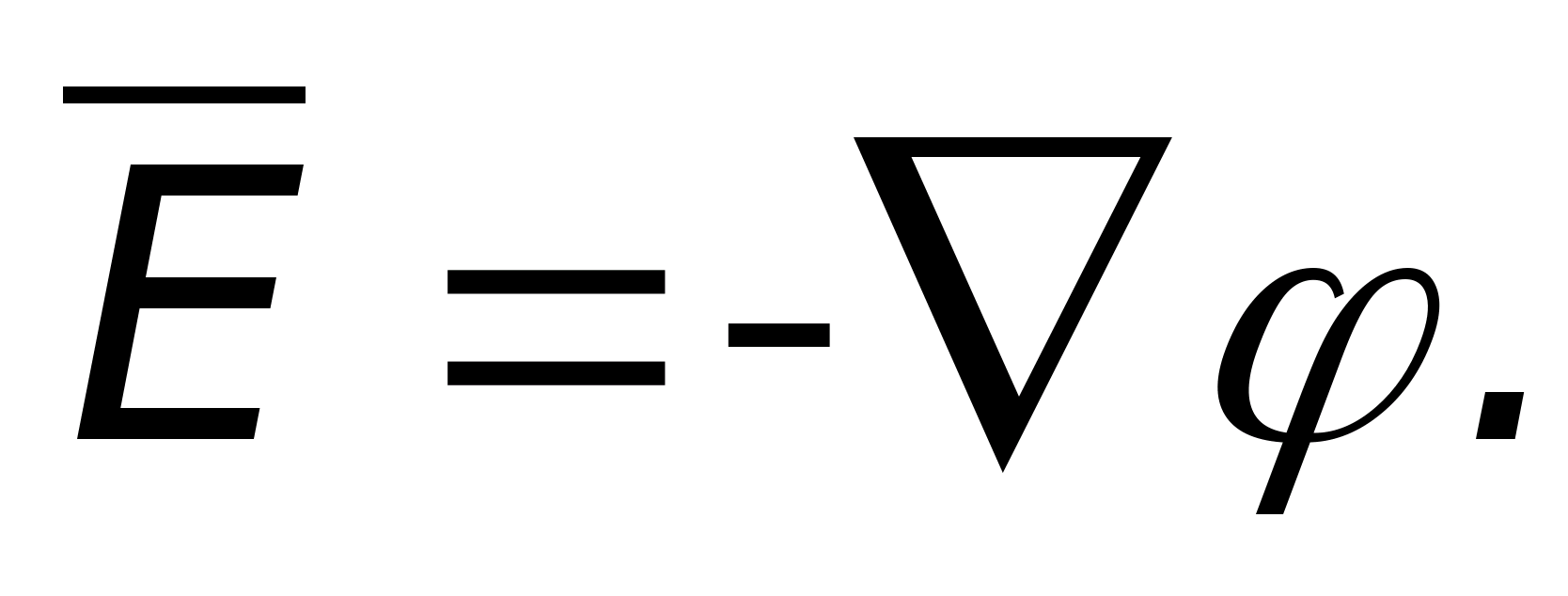
Polaryzacja materii
W substancjach rozróżnia się ładunki wolne i związane. Ładunki swobodne to takie, które pod wpływem sił pola mogą swobodnie poruszać się w substancji; ich ruch nie jest ograniczony siłami wewnątrzcząsteczkowymi. Przez związane ładunki rozumiemy te, które pod wpływem sił pola mogą poruszać się jedynie wewnątrz cząsteczki. Ładunki związane są nierozerwalnie związane z materią, dlatego suma ładunków dodatnich jest równa sumie ładunków ujemnych.
D 
Ciała elektryczne w polu elektrostatycznym są spolaryzowane. Przez polaryzację rozumie się uporządkowaną zmianę rozmieszczenia związanych ładunków pod wpływem sił pola. Polaryzację można wyraźnie pokazać korzystając z ryc. 11.5, który przedstawia ciało przy braku pola elektrostatycznego i w jego obecności. Jeśli nie ma pola, wówczas cząsteczki (dipole) znajdują się w nieładzie chaotycznym (ryc. 11.5, a). W ciele spolaryzowanym ładunki związane dodatnio przesuwają się w stronę wyższego potencjału, a ujemne w stronę niższego potencjału (ryc. 11.5, b) i przesuwają się tak bardzo, że siły pola elektrycznego równoważą siły wewnątrzcząsteczkowe. W wyniku polaryzacji na powierzchni substancji pojawiają się dodatnie lub ujemne ładunki związane, a suma pierwszego z nich jest dokładnie równa sumie drugiego. Dipole tworzą własne pola. W substancji niespolaryzowanej ich całkowity efekt wynosi zero, ale w substancji spolaryzowanej tak nie jest; prowadzi to do osłabienia powstałego pola i należy to wziąć pod uwagę. W tym celu wprowadzono pojęcie momentu elektrycznego dipola. Moment elektryczny dwóch ładunków o jednakowej wielkości i przeciwnych znakach, znajdujących się w pewnej odległości od siebie l, praca nazywa się  To jest wektor skierowany z - Q k + Q(ryc. 11.6). Pod wpływem pola zewnętrznego dipole substancji mają tendencję do orientowania się w taki sposób, że ich momenty elektryczne pokrywają się z natężeniem pola zewnętrznego. Praktyczne znaczenie ma oczywiście nie tylko jeden dipol i jego moment elektryczny (jest niezwykle mały), ale suma momentów elektrycznych dipoli znajdujących się w jednostkowej objętości, co zwykle nazywa się wektorem polaryzacji
To jest wektor skierowany z - Q k + Q(ryc. 11.6). Pod wpływem pola zewnętrznego dipole substancji mają tendencję do orientowania się w taki sposób, że ich momenty elektryczne pokrywają się z natężeniem pola zewnętrznego. Praktyczne znaczenie ma oczywiście nie tylko jeden dipol i jego moment elektryczny (jest niezwykle mały), ale suma momentów elektrycznych dipoli znajdujących się w jednostkowej objętości, co zwykle nazywa się wektorem polaryzacji  , tj.
, tj.  W przypadku większości dielektryków wektor polaryzacji jest proporcjonalny do natężenia pola
W przypadku większości dielektryków wektor polaryzacji jest proporcjonalny do natężenia pola  oraz współczynnik proporcjonalności pomiędzy nimi k nazywana podatnością elektryczną.
oraz współczynnik proporcjonalności pomiędzy nimi k nazywana podatnością elektryczną.
Oprócz wielkości wektorowych omówionych powyżej  i , którego fizyczne znaczenie wyjaśniliśmy, w teorii pola do obliczeń wprowadza się inny wektor
i , którego fizyczne znaczenie wyjaśniliśmy, w teorii pola do obliczeń wprowadza się inny wektor  , który nazywany jest wektorem przemieszczenia elektrycznego lub wektorem indukcji elektrycznej. Definiuje się to następująco: gdzie
, który nazywany jest wektorem przemieszczenia elektrycznego lub wektorem indukcji elektrycznej. Definiuje się to następująco: gdzie 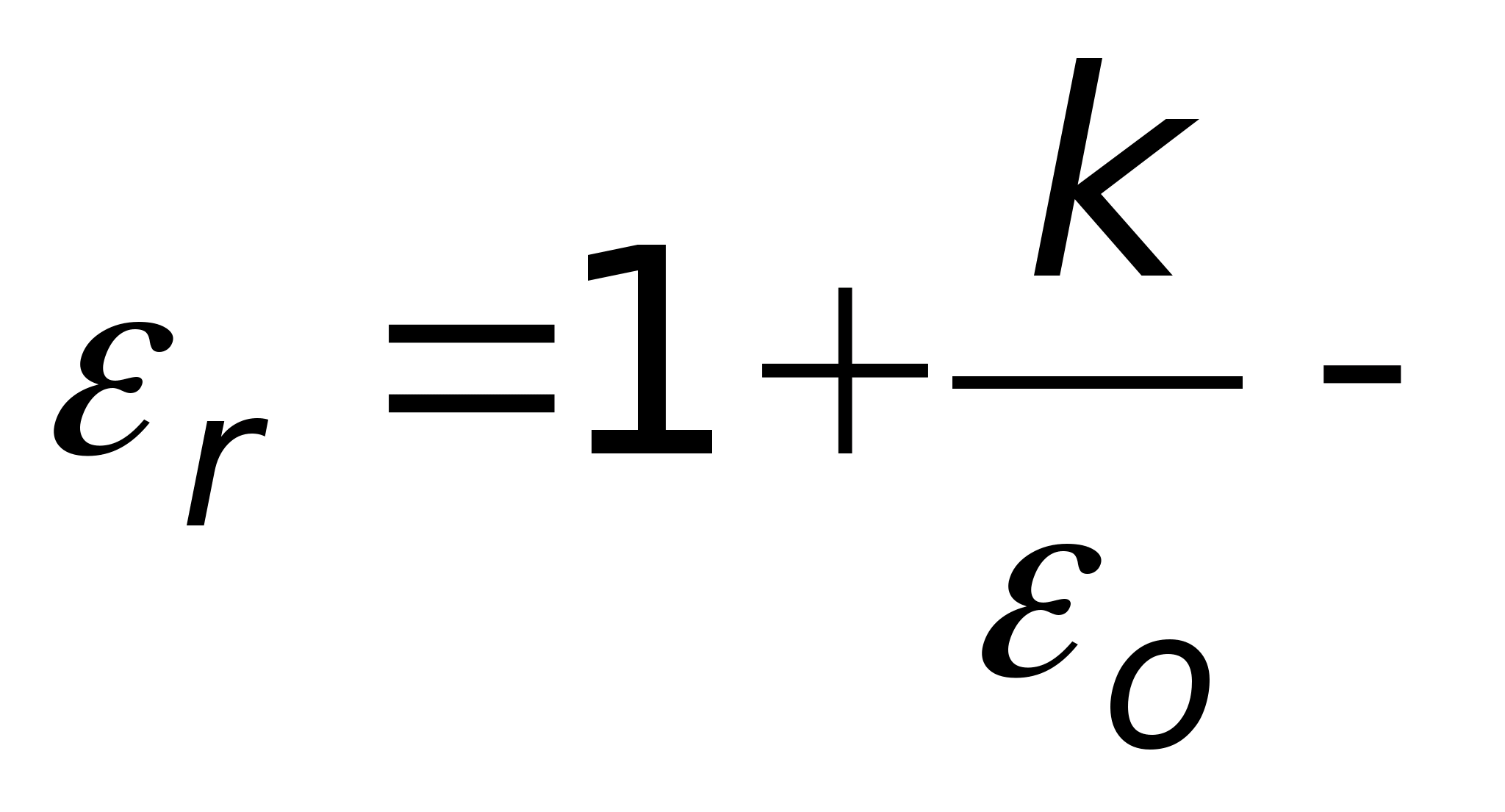 nazywa się względną stałą dielektryczną ośrodka, w którym pole jest utworzone, oraz
nazywa się względną stałą dielektryczną ośrodka, w którym pole jest utworzone, oraz  bezwzględna stała dielektryczna ośrodka, w którym pole jest wytworzone.
bezwzględna stała dielektryczna ośrodka, w którym pole jest wytworzone. 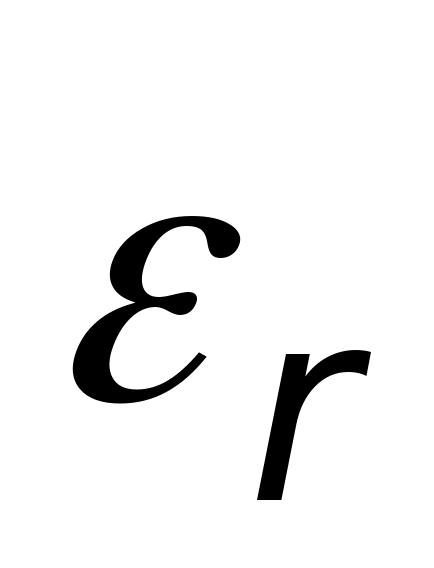 pokazuje, ile razy właściwości elektryczne ośrodka różnią się od właściwości próżni (różnica ta wynika z polaryzacji). Dla wszystkich środowisk jest ona ustalana eksperymentalnie i podana w podręcznikach.
pokazuje, ile razy właściwości elektryczne ośrodka różnią się od właściwości próżni (różnica ta wynika z polaryzacji). Dla wszystkich środowisk jest ona ustalana eksperymentalnie i podana w podręcznikach.
Twierdzenie Gaussa
Twierdzenie Gaussa jest podstawowym prawem pola elektrostatycznego. Zostało to odkryte eksperymentalnie i zapisane matematycznie w następujący sposób 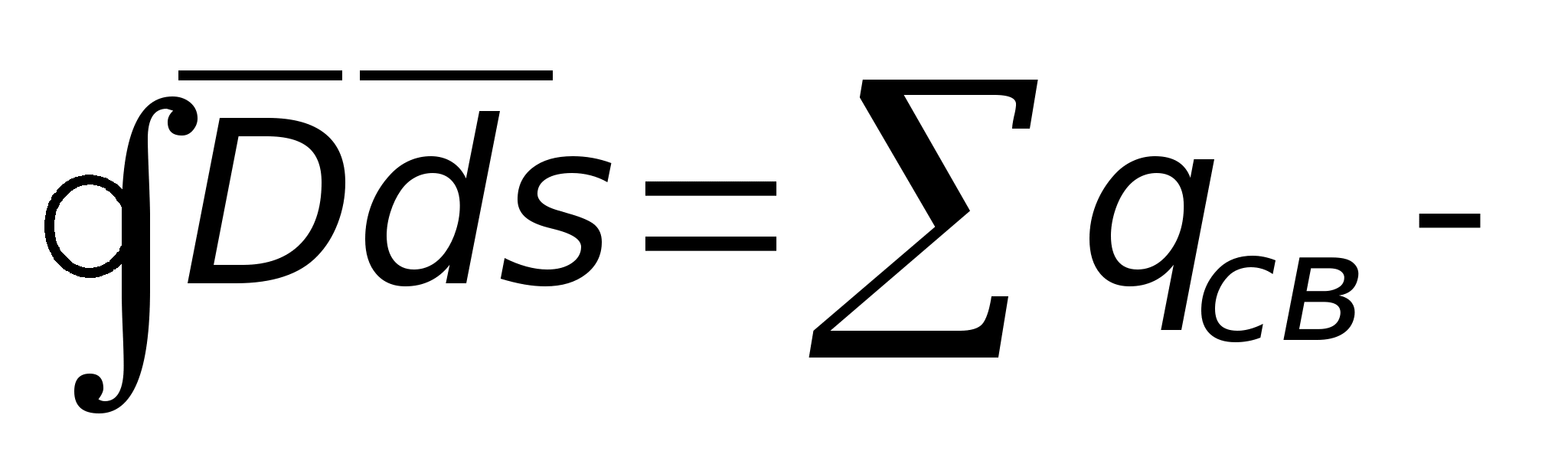 przepływ wektora przemieszczenia elektrycznego przez dowolną zamkniętą powierzchnię otaczającą pewną objętość jest równy sumie algebraicznej swobodnych ładunków znajdujących się wewnątrz tej powierzchni (w sumie
przepływ wektora przemieszczenia elektrycznego przez dowolną zamkniętą powierzchnię otaczającą pewną objętość jest równy sumie algebraicznej swobodnych ładunków znajdujących się wewnątrz tej powierzchni (w sumie 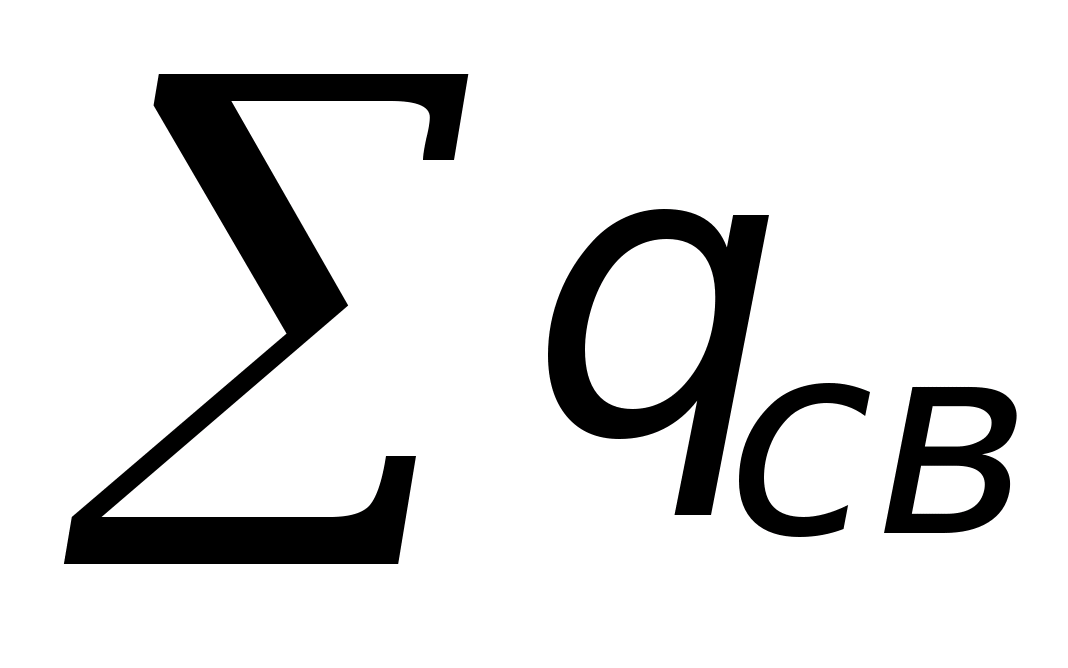 opłaty pobierane są wraz z ich znakami). Od
opłaty pobierane są wraz z ich znakami). Od  To
To  .
.  Do mediów jednorodnych i izotropowych
Do mediów jednorodnych i izotropowych 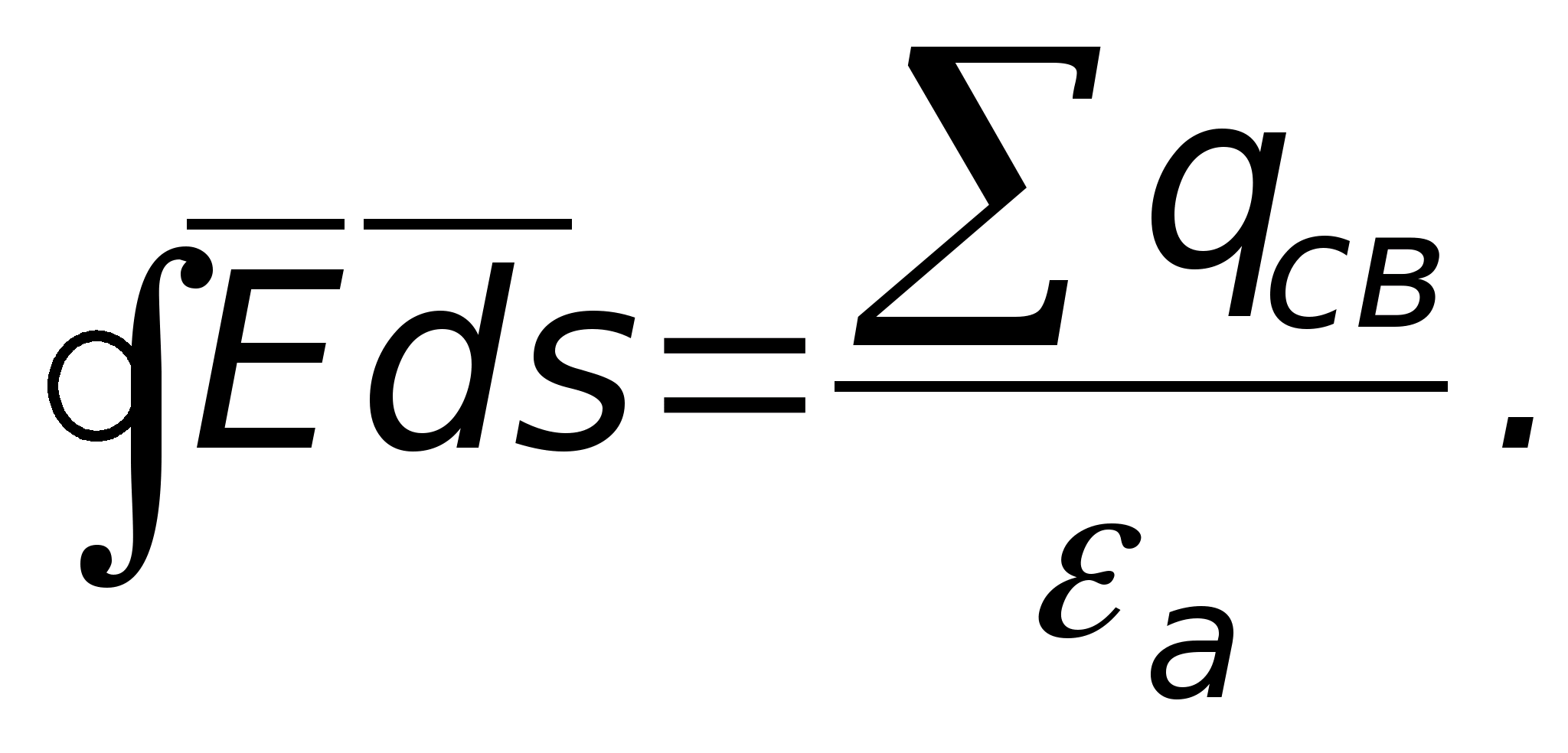 jest wartością stałą i można ją wówczas wyjąć ze znaku całki Co ciekawe, przepływ wektorowy D mi Lub mi zależy tylko i nie zależy od rozmieszczenia ładunków wewnątrz zamkniętej powierzchni. Wektor przepływu
jest wartością stałą i można ją wówczas wyjąć ze znaku całki Co ciekawe, przepływ wektorowy D mi Lub mi zależy tylko i nie zależy od rozmieszczenia ładunków wewnątrz zamkniętej powierzchni. Wektor przepływu 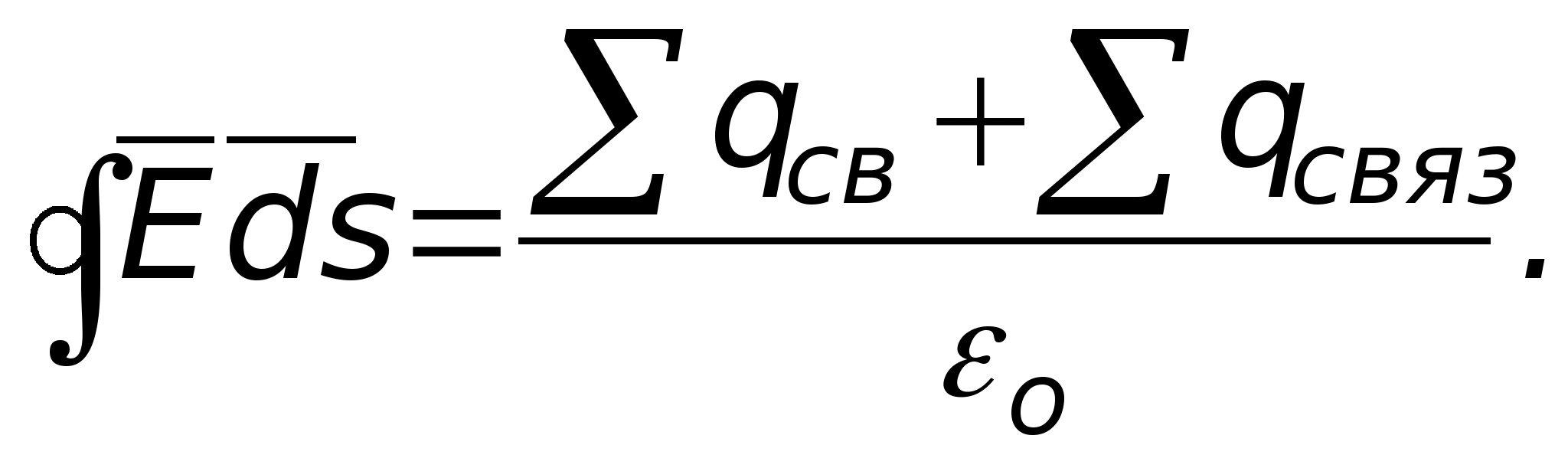 tworzone są nie tylko przez opłaty bezpłatne, ale także przez opłaty powiązane. Te ostatnie można uwzględnić nie poprzez , ale poprzez osobną sumę związanych ładunków i wówczas wzór na twierdzenie Gaussa wygląda następująco:
tworzone są nie tylko przez opłaty bezpłatne, ale także przez opłaty powiązane. Te ostatnie można uwzględnić nie poprzez , ale poprzez osobną sumę związanych ładunków i wówczas wzór na twierdzenie Gaussa wygląda następująco:
Te trzy wzory stanowią integralną formę twierdzenia Gaussa, które można zastosować z dużą wydajnością i prostotą do obliczenia natężenia pola w dowolnym punkcie, jeśli można przez niego przeciągnąć zamkniętą powierzchnię, której wszystkie punkty znajdują się w tych samych warunkach pod względem do ładunków, tworząc pole. Jako przykład obliczmy pole utworzone przez ładunek punktowy.  T
T 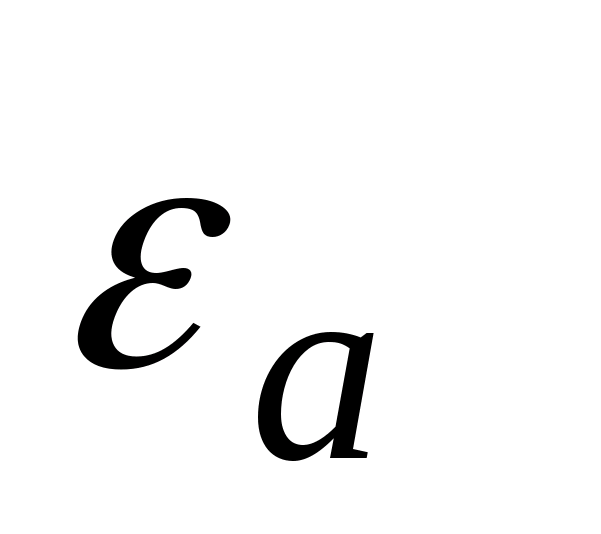 Ładunek punktowy to ładunek umieszczony na ciele o bardzo małych wymiarach geometrycznych. Na ryc. 11.7 będzie on przedstawiony jako punkt (stąd nazwa). Załóżmy, że ładunek ten jest dodatni i znajduje się w ośrodku przepuszczalnym R.
Ładunek punktowy to ładunek umieszczony na ciele o bardzo małych wymiarach geometrycznych. Na ryc. 11.7 będzie on przedstawiony jako punkt (stąd nazwa). Załóżmy, że ładunek ten jest dodatni i znajduje się w ośrodku przepuszczalnym R.  Weźmy dowolny punkt oddzielony odległością mi z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory I mi ds
Weźmy dowolny punkt oddzielony odległością mi z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory I mi ds 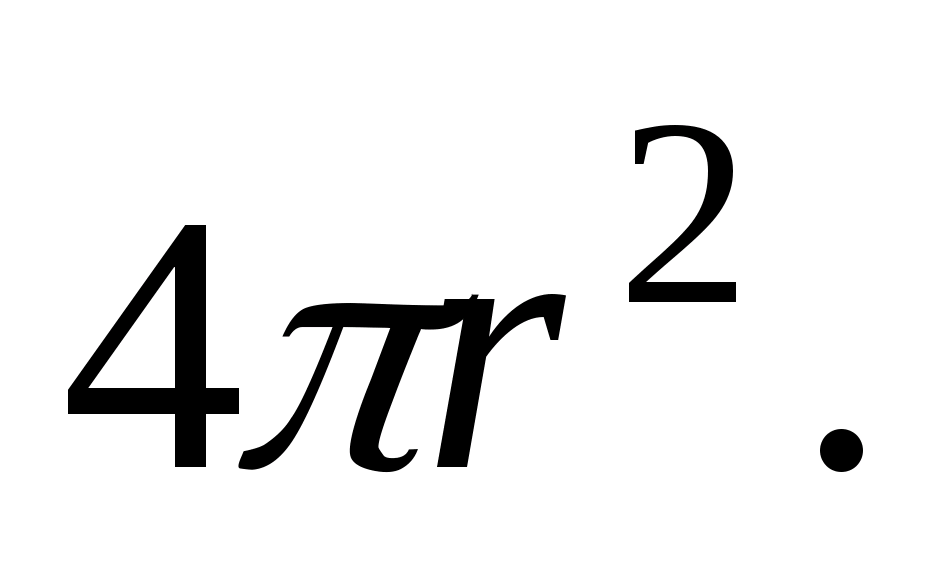 pokrywają się, wówczas ich produkt pokrywa się z produktem modułów. Ponadto we wszystkich punktach rozważanej kuli wielkość wektora
pokrywają się, wówczas ich produkt pokrywa się z produktem modułów. Ponadto we wszystkich punktach rozważanej kuli wielkość wektora 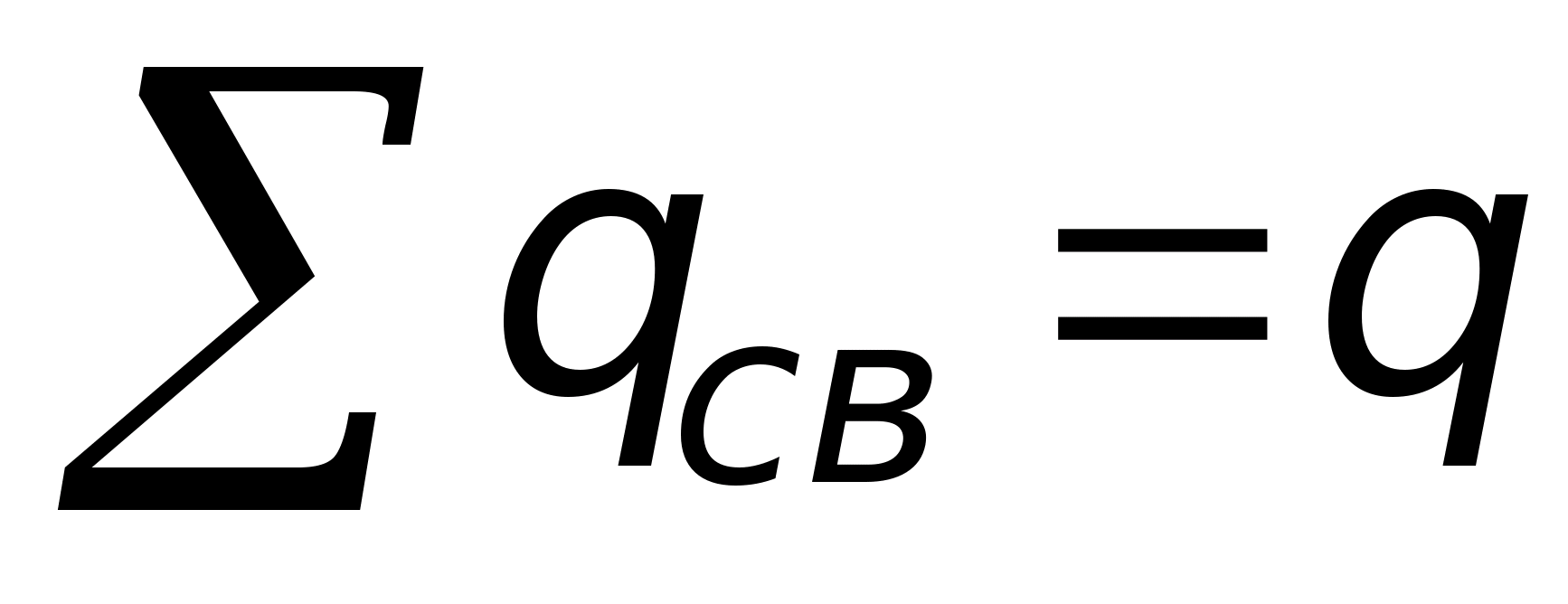 to samo ze względu na symetrię. Biorąc to pod uwagę, mamy: ponieważ powierzchnia kuli jest równa
to samo ze względu na symetrię. Biorąc to pod uwagę, mamy: ponieważ powierzchnia kuli jest równa  Suma bezpłatnych opłat jest równa tylko danej opłacie punktowej R 2 .
Suma bezpłatnych opłat jest równa tylko danej opłacie punktowej R 2 .
Obliczmy potencjał w tym polu na podstawie wzoru. Jeśli weźmiemy pod uwagę, że napięcie, a zatem i potencjał, zależą tylko od promienia, wówczas ostatni wzór zostanie przepisany w następujący sposób 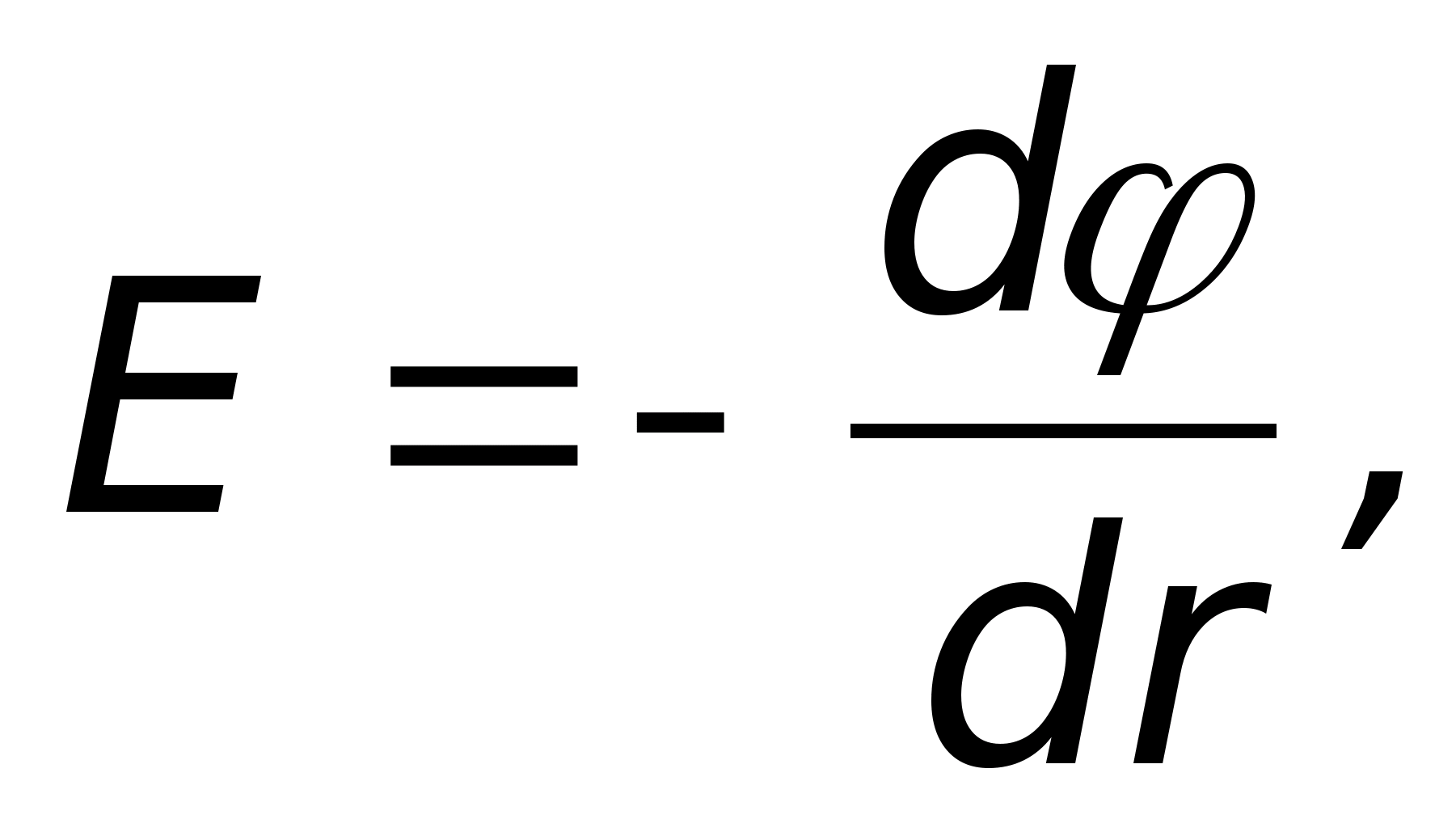 Gdzie
Gdzie 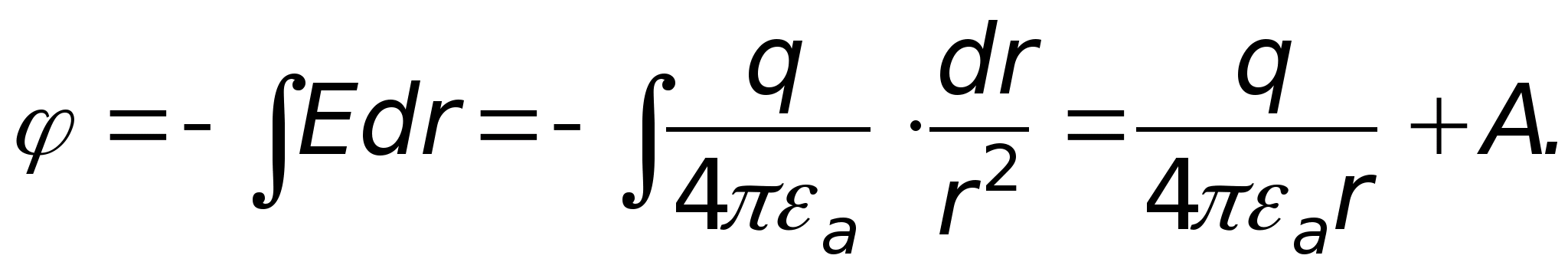 Wynika z tego, że potencjał w danym polu zmienia się odwrotnie proporcjonalnie do R. Stała całkowania A zależy od tego, gdzie znajduje się punkt o potencjale zerowym.
Wynika z tego, że potencjał w danym polu zmienia się odwrotnie proporcjonalnie do R. Stała całkowania A zależy od tego, gdzie znajduje się punkt o potencjale zerowym.
Całkowa postać zapisu twierdzenia Gaussa nie daje odpowiedzi na pytanie, jak natężenie pola w danym punkcie jest powiązane z ładunkiem w tym samym punkcie. Odpowiedź na to pytanie daje różniczkowa postać tego twierdzenia, która wynika z postaci całkowej. Do tego wyrażenie 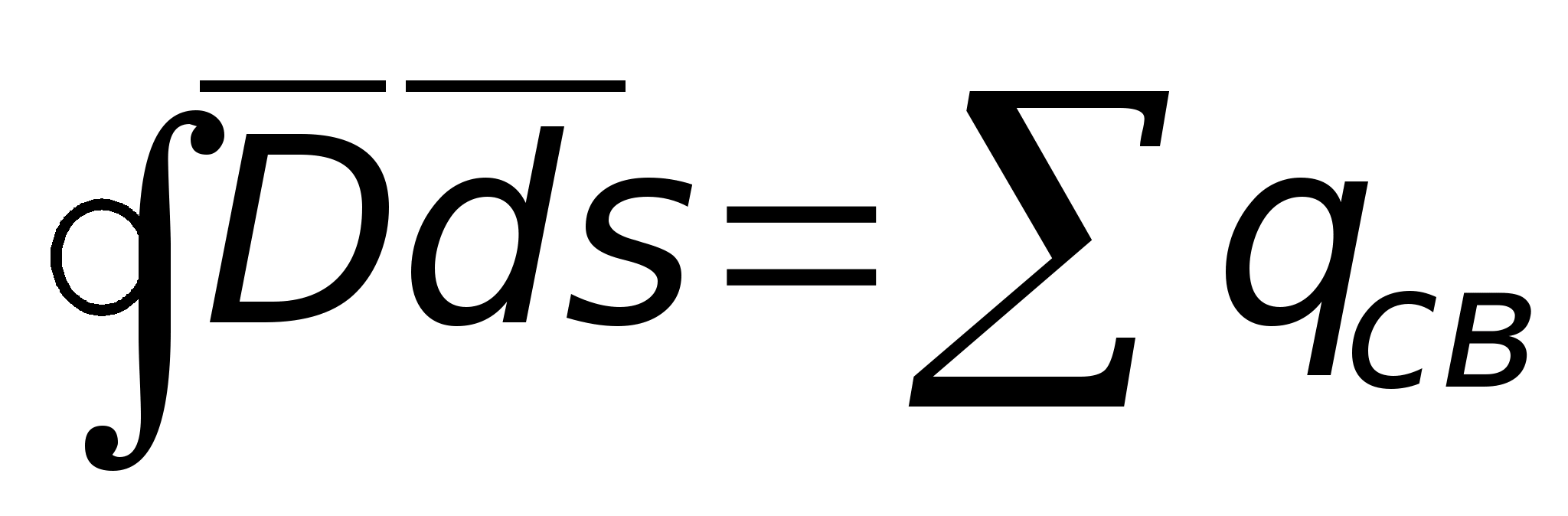 podzielić przez objętość ograniczoną powierzchnią całkowania
podzielić przez objętość ograniczoną powierzchnią całkowania 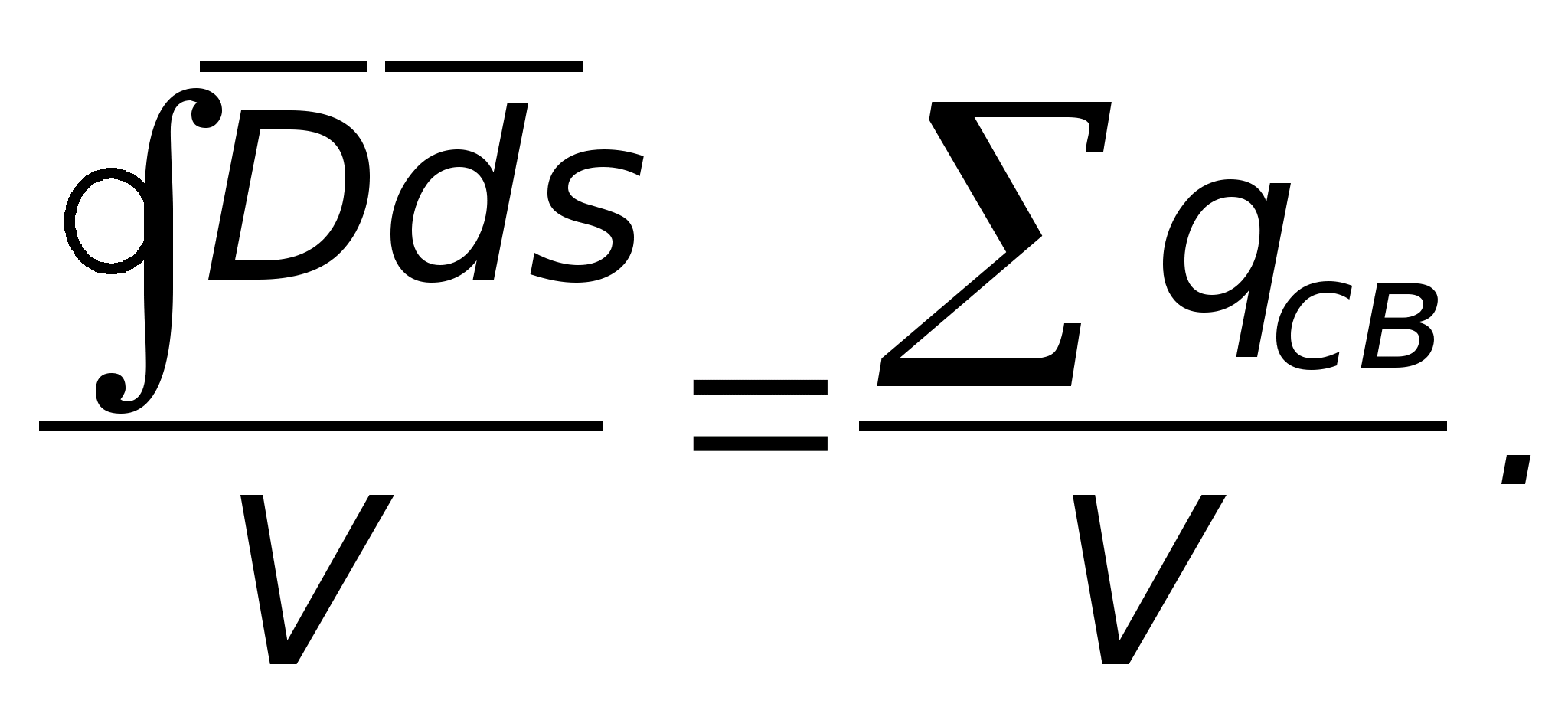 Zależność ta obowiązuje dla objętości o dowolnym rozmiarze. Skierujmy to na zero (mówią, że zmniejszymy powierzchnię do pewnego punktu). Następnie
Zależność ta obowiązuje dla objętości o dowolnym rozmiarze. Skierujmy to na zero (mówią, że zmniejszymy powierzchnię do pewnego punktu). Następnie  Limit współczynnika strumienia wektorowego Co ciekawe, przepływ wektorowy przez zamkniętą powierzchnię ograniczającą pewną objętość do wartości tej objętości nazywa się rozbieżnością wektora Co ciekawe, przepływ wektorowy
(
Limit współczynnika strumienia wektorowego Co ciekawe, przepływ wektorowy przez zamkniętą powierzchnię ograniczającą pewną objętość do wartości tej objętości nazywa się rozbieżnością wektora Co ciekawe, przepływ wektorowy
(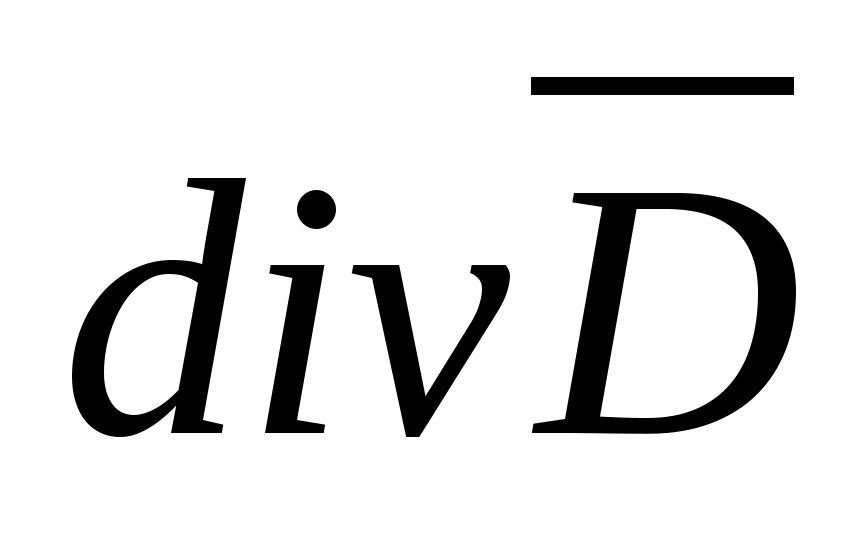 ) albo źródło, albo rozbieżność. Po prawej stronie ostatniej równości jest gęstość nasypowa bezpłatna opłata ρ
Św.. Następnie
) albo źródło, albo rozbieżność. Po prawej stronie ostatniej równości jest gęstość nasypowa bezpłatna opłata ρ
Św.. Następnie  To jest twierdzenie Gaussa w postaci różniczkowej. Wyjaśnijmy jego istotę za pomocą trzech przypadków, o
To jest twierdzenie Gaussa w postaci różniczkowej. Wyjaśnijmy jego istotę za pomocą trzech przypadków, o ![]() pokazano na ryc. 11.8. Jeżeli w rozważanym punkcie pola gęstość objętościowa ładunku swobodnego jest dodatnia, to z nieskończenie małej objętości otaczającej ten punkt linie wektora Co ciekawe, przepływ wektorowy pochodzą (źródło jest dodatnie, rozbieżność jest dodatnia, rozbieżność jest dodatnia). Jeżeli w rozważanym punkcie pola gęstość objętościowa ładunku swobodnego jest ujemna, to w nieskończenie małej objętości otaczającej ten punkt linie wektora Co ciekawe, przepływ wektorowy uwzględnione (źródło ujemne, rozbieżność ujemna, rozbieżność ujemna). I wreszcie, jeśli w rozważanym punkcie nie ma darmowego ładunku, to w takim punkcie nie ma ani drenażu, ani źródła linii wektorowych Co ciekawe, przepływ wektorowy, tj. w takim punkcie linii wektora Co ciekawe, przepływ wektorowy nie zaczynaj i nie kończ, ale przenikaj nieskończenie małą objętość otaczającą dany punkt.
pokazano na ryc. 11.8. Jeżeli w rozważanym punkcie pola gęstość objętościowa ładunku swobodnego jest dodatnia, to z nieskończenie małej objętości otaczającej ten punkt linie wektora Co ciekawe, przepływ wektorowy pochodzą (źródło jest dodatnie, rozbieżność jest dodatnia, rozbieżność jest dodatnia). Jeżeli w rozważanym punkcie pola gęstość objętościowa ładunku swobodnego jest ujemna, to w nieskończenie małej objętości otaczającej ten punkt linie wektora Co ciekawe, przepływ wektorowy uwzględnione (źródło ujemne, rozbieżność ujemna, rozbieżność ujemna). I wreszcie, jeśli w rozważanym punkcie nie ma darmowego ładunku, to w takim punkcie nie ma ani drenażu, ani źródła linii wektorowych Co ciekawe, przepływ wektorowy, tj. w takim punkcie linii wektora Co ciekawe, przepływ wektorowy nie zaczynaj i nie kończ, ale przenikaj nieskończenie małą objętość otaczającą dany punkt.
Od  To
To  Do mediów jednorodnych i izotropowych
Do mediów jednorodnych i izotropowych  jest wartością stałą i można ją usunąć ze znaku div, wówczas otrzymujemy:
jest wartością stałą i można ją usunąć ze znaku div, wówczas otrzymujemy:  Jeśli uwzględni się zjawisko polaryzacji przy użyciu związanych ładunków, to ostatnie wyrażenie można przepisać w następujący sposób
Jeśli uwzględni się zjawisko polaryzacji przy użyciu związanych ładunków, to ostatnie wyrażenie można przepisać w następujący sposób 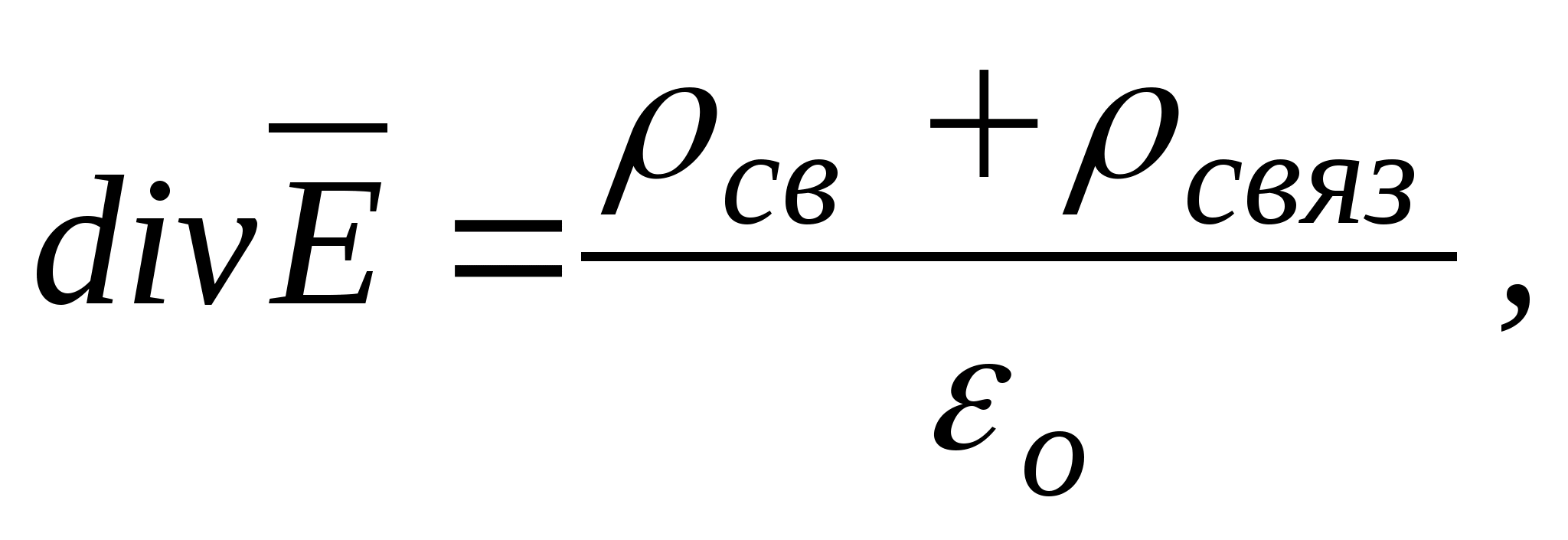 Gdzie ρ
Gdzie ρ
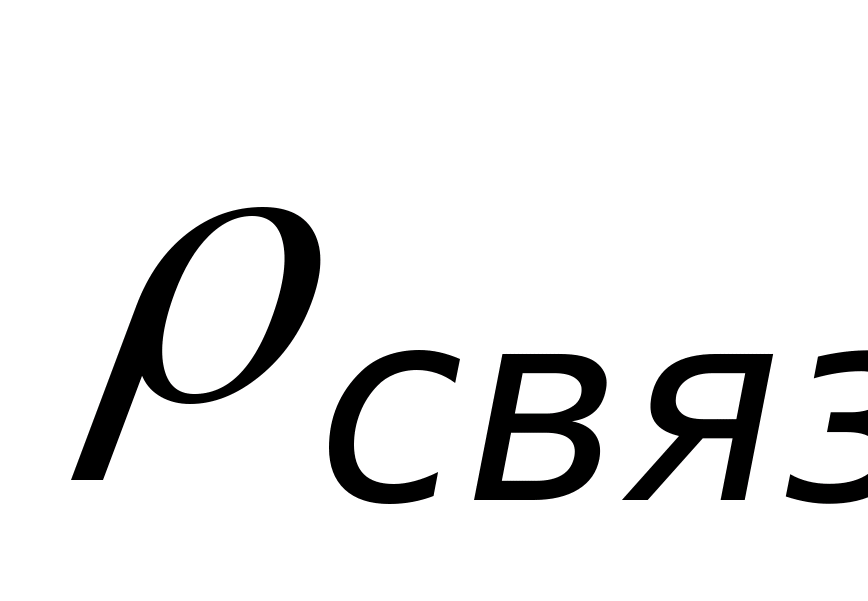
połączenie- gęstość objętościowa związanych ładunków. Pomijanie wyników wyrażeń 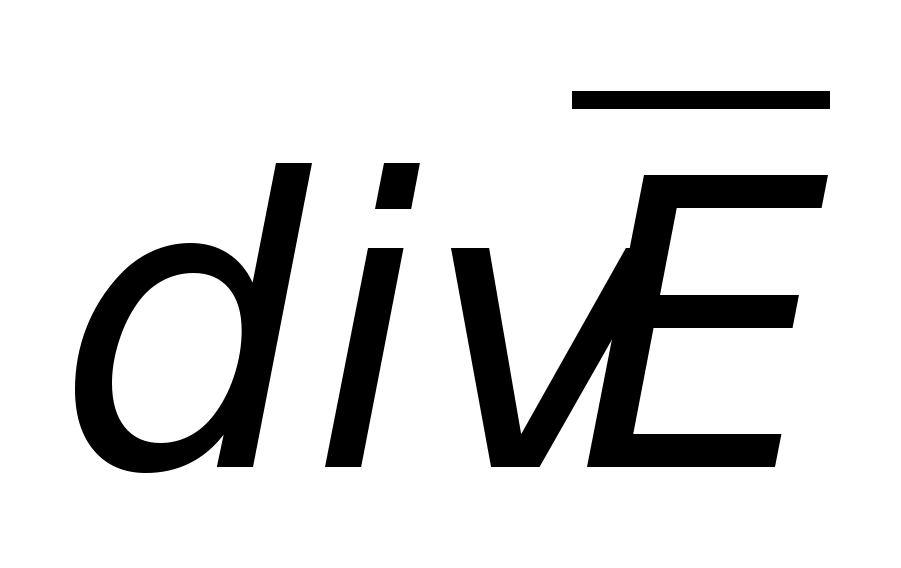 , zapiszmy to w prostokątnym układzie współrzędnych
, zapiszmy to w prostokątnym układzie współrzędnych  jest to suma pochodnych cząstkowych rzutów wektorowych mi wzdłuż trzech osi współrzędnych. Pokażmy, że iloczyn skalarny operatora nabla i wektora mi oznacza wzięcie rozbieżności z tym ostatnim:
jest to suma pochodnych cząstkowych rzutów wektorowych mi wzdłuż trzech osi współrzędnych. Pokażmy, że iloczyn skalarny operatora nabla i wektora mi oznacza wzięcie rozbieżności z tym ostatnim:
W związku z tym twierdzenie Gaussa w formie różniczkowej jest często zapisywane w następujący sposób 
Równania Poissona i Laplace'a
Równania Poissona i Laplace'a wynikają z twierdzenia Gaussa w formie różniczkowej i należą również do podstawowych równań elektrostatyki. Rzeczywiście, wiadomo, że. Jednocześnie zastępując pierwsze wyrażenie drugim, otrzymujemy  Lub
Lub  Zamiast rozbieżności i gradientu możesz użyć operatora nabla i wtedy otrzymamy
Zamiast rozbieżności i gradientu możesz użyć operatora nabla i wtedy otrzymamy  .
.
 nazywa się Laplacianem i oznacza się go w następujący sposób
nazywa się Laplacianem i oznacza się go w następujący sposób 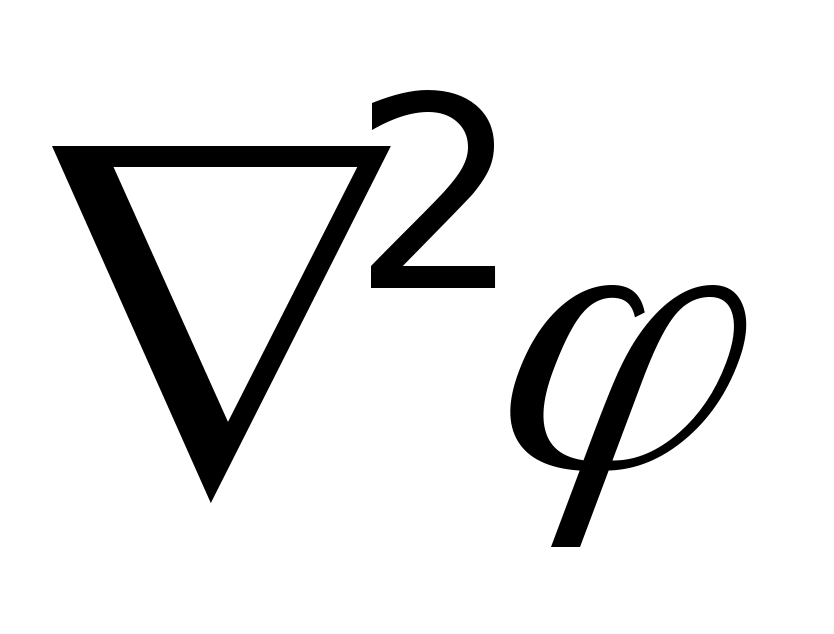 . Następnie
. Następnie  . To jest równanie Poissona. Rozwińmy Laplaciana potencjału w prostokątnym układzie współrzędnych: ponieważ iloczyn podobnych wektorów jednostkowych daje jeden, a w przeciwieństwie do jednostkowych - zero.
. To jest równanie Poissona. Rozwińmy Laplaciana potencjału w prostokątnym układzie współrzędnych: ponieważ iloczyn podobnych wektorów jednostkowych daje jeden, a w przeciwieństwie do jednostkowych - zero.
Szczególna postać równania Poissona dla ρ
Św.=0 nazywa się równaniem Laplace’a. Wygląda to tak 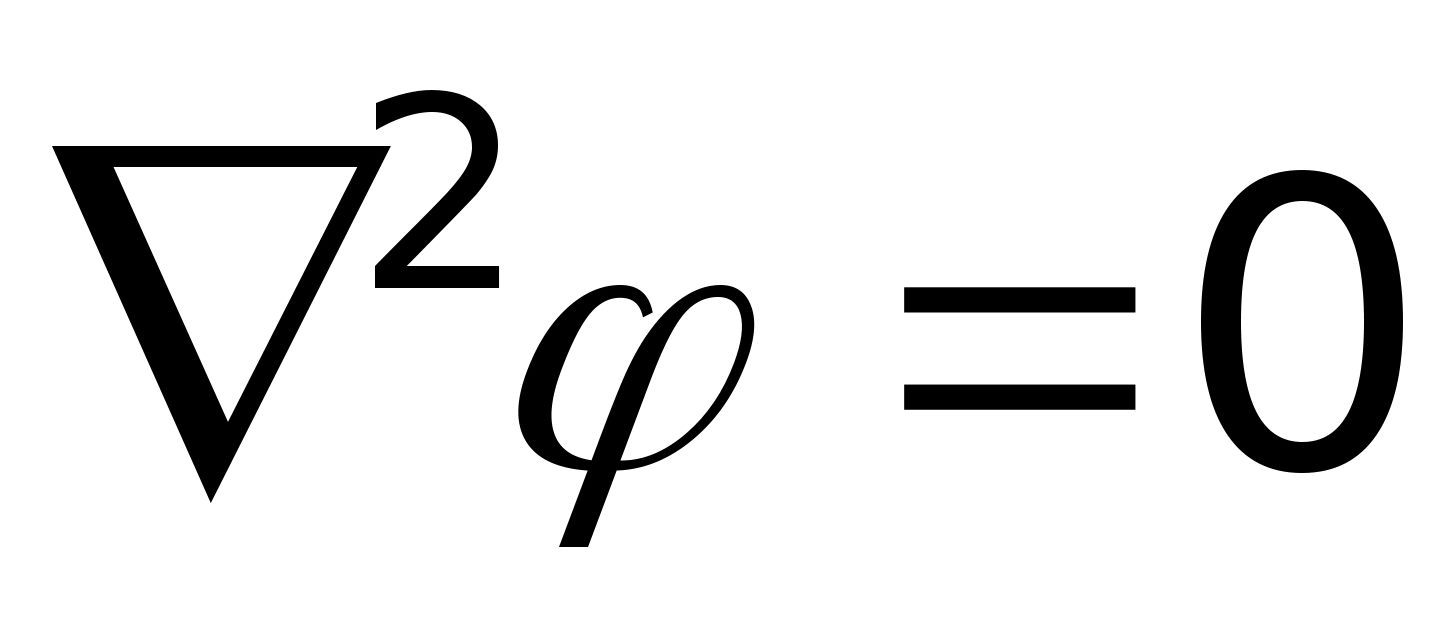 lub w prostokątnym układzie współrzędnych
lub w prostokątnym układzie współrzędnych 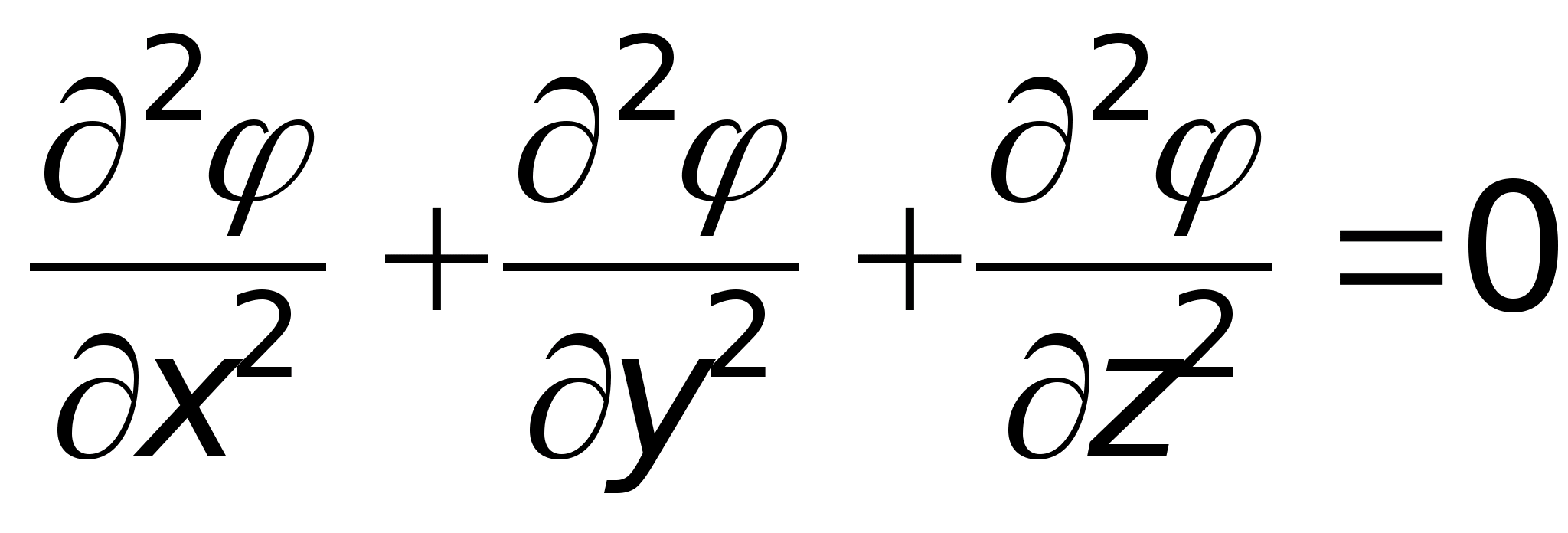 . Równanie Laplace'a opisuje obszary pola elektrostatycznego niezajęte przez ładunek swobodny.
. Równanie Laplace'a opisuje obszary pola elektrostatycznego niezajęte przez ładunek swobodny.
W  W elektrostatyce istnieją problemy, które znacznie łatwiej rozwiązać nie w prostokątnym, ale w cylindrycznym lub sferycznym układzie współrzędnych (ryc. 11.9). Wyrażenie Laplaciana potencjału w cylindrycznym układzie współrzędnych ma postać:
W elektrostatyce istnieją problemy, które znacznie łatwiej rozwiązać nie w prostokątnym, ale w cylindrycznym lub sferycznym układzie współrzędnych (ryc. 11.9). Wyrażenie Laplaciana potencjału w cylindrycznym układzie współrzędnych ma postać:  i sferyczne.
i sferyczne.
Rozwiązanie równań Poissona i Laplace'a pod względem matematycznym jest zadaniem bardzo trudnym, ale ich rozwiązanie pozwala wyznaczyć prawo zmiany potencjału na podstawie znanego rozkładu ładunku. Przy rozwiązywaniu tych równań pojawiają się stałe całkowania, które wyznacza się na podstawie warunków brzegowych.
Warunki brzegowe w polu elektrostatycznym
P 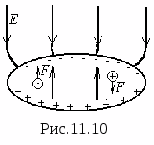 Warunki brzegowe oznaczają warunki, jakie spełnia pole na styku dwóch różne środowiska. Zanim przejdziemy do omówienia warunków brzegowych, rozważmy zachowanie ciała przewodzącego w polu elektrostatycznym. Ciało zawierające wolne ładunki nazywa się przewodzącym. Niech ciało przewodzące zostanie umieszczone w polu elektrostatycznym (rys. 11.10). Wtedy na każdy ładunek swobodny od strony pola zacznie działać siła, pod wpływem której ładunki swobodne dodatnie będą przesuwać się w stronę potencjału niskiego, a ładunki ujemne ujemne w stronę potencjału wysokiego. Ruch ładunków jest możliwy tylko wewnątrz ciała przewodzącego, dlatego gromadzą się one na jego powierzchni (dodatni po stronie niskiego potencjału i ujemny po stronie wysokiego potencjału). Zjawisko to nazywa się indukcją elektrostatyczną, a ładunki zgromadzone na powierzchni przewodnika nazywane są indukowanymi.
Warunki brzegowe oznaczają warunki, jakie spełnia pole na styku dwóch różne środowiska. Zanim przejdziemy do omówienia warunków brzegowych, rozważmy zachowanie ciała przewodzącego w polu elektrostatycznym. Ciało zawierające wolne ładunki nazywa się przewodzącym. Niech ciało przewodzące zostanie umieszczone w polu elektrostatycznym (rys. 11.10). Wtedy na każdy ładunek swobodny od strony pola zacznie działać siła, pod wpływem której ładunki swobodne dodatnie będą przesuwać się w stronę potencjału niskiego, a ładunki ujemne ujemne w stronę potencjału wysokiego. Ruch ładunków jest możliwy tylko wewnątrz ciała przewodzącego, dlatego gromadzą się one na jego powierzchni (dodatni po stronie niskiego potencjału i ujemny po stronie wysokiego potencjału). Zjawisko to nazywa się indukcją elektrostatyczną, a ładunki zgromadzone na powierzchni przewodnika nazywane są indukowanymi.
Choć suma ładunków dodatnich jest dokładnie równa sumie ładunków ujemnych i generalnie ciało jest elektrycznie obojętne (o ile nie zostało wcześniej naładowane), to indukowane ładunki tworzą własne pole, co prowadzi do zmiany powstałe pole wewnątrz ciała oraz w jego pobliżu i w jego sąsiedztwie.  Wszystkie punkty ciała przewodzącego mają ten sam potencjał, gdyż jeśli założymy, że między dwoma punktami istnieje różnica potencjałów, to pod wpływem tej różnicy będzie płynął prąd i potencjały się zrównoważą. Ponieważ wszystkie punkty ciała przewodzącego mają ten sam potencjał, natężenie pola elektrostatycznego wewnątrz niego
Wszystkie punkty ciała przewodzącego mają ten sam potencjał, gdyż jeśli założymy, że między dwoma punktami istnieje różnica potencjałów, to pod wpływem tej różnicy będzie płynął prąd i potencjały się zrównoważą. Ponieważ wszystkie punkty ciała przewodzącego mają ten sam potencjał, natężenie pola elektrostatycznego wewnątrz niego
te. wewnątrz ciała przewodzącego nie ma pola. Z fizycznego punktu widzenia tłumaczy się to faktem, że pole zewnętrzne jest całkowicie kompensowane przez pole indukowanych ładunków (patrz rys. 11.10). Ładunków indukowanych jest tak wiele i są one rozmieszczone dokładnie w taki sposób, że pola wewnątrz ciała przewodzącego są całkowicie kompensowane. Zatem objętość zajmowana przez ciało przewodzące jest ekwipotencjalna. Opisana właściwość ciał przewodzących jest wykorzystywana w praktyce do ekranowania urządzeń przed działaniem zewnętrznych pól elektrostatycznych. Warunki na styku dielektryka i ciała przewodzącego. mi Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru ( T =0), a wektor przemieszczenia elektrycznego jest liczbowo równy gęstości powierzchniowej indukowanego ładunku ().
D  D=σ mi będzie skierowany wzdłuż linii łączącej te punkty i będzie wyznaczany w następujący sposób
D=σ mi będzie skierowany wzdłuż linii łączącej te punkty i będzie wyznaczany w następujący sposób 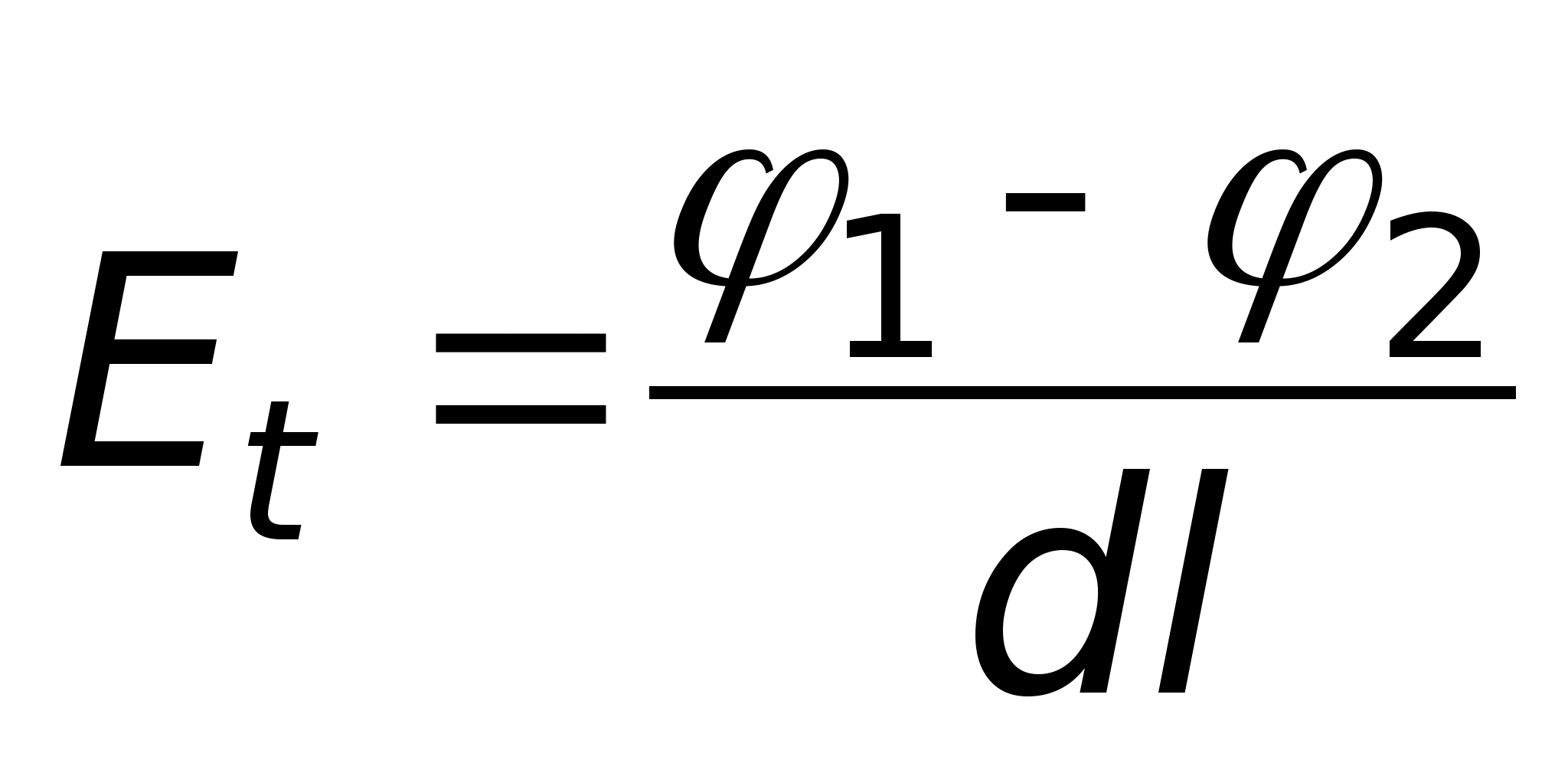 , Ale
, Ale 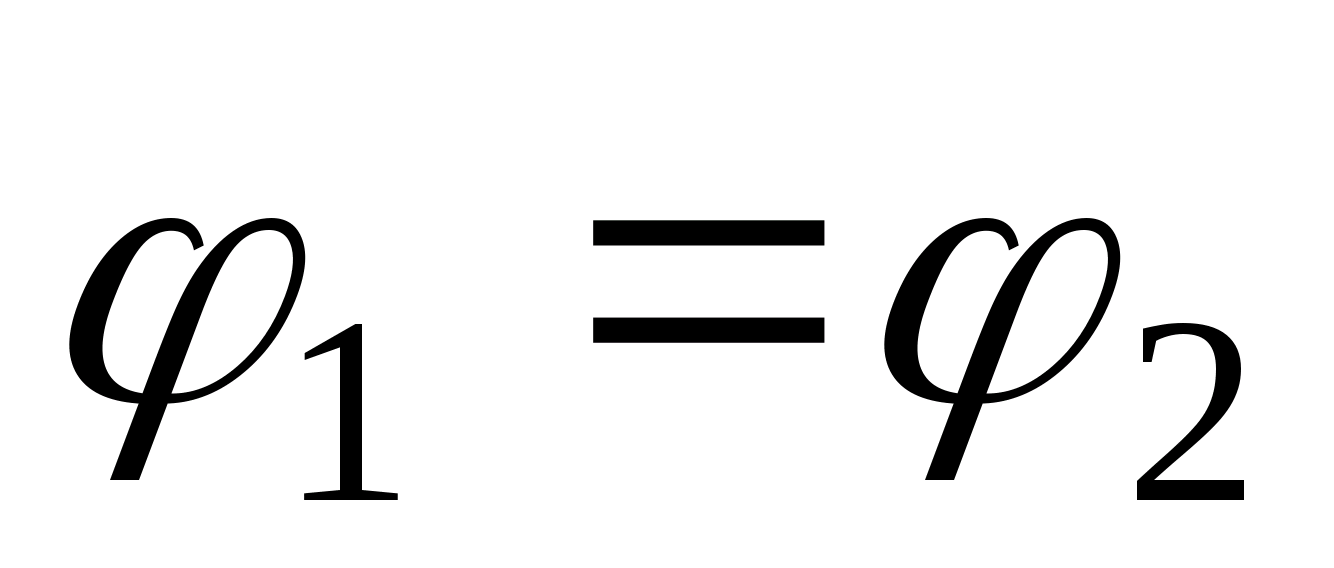 , ponieważ punkty 1 i 2 należą zarówno do przewodnika, jak i
, ponieważ punkty 1 i 2 należą zarówno do przewodnika, jak i 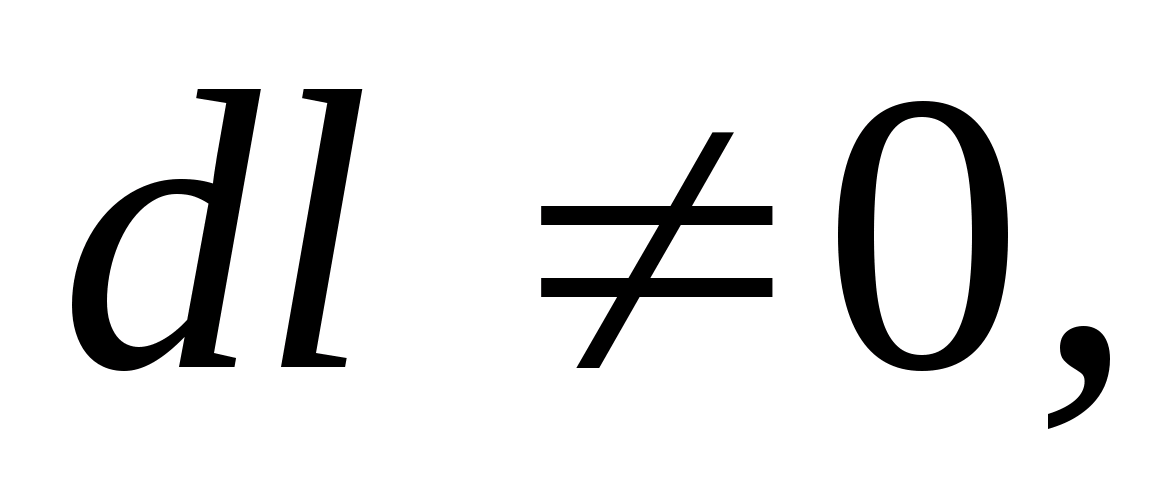 Dlatego mi Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru (=0, co należało udowodnić. Zatem linie siły pola elektrostatycznego zbliżają się do powierzchni przewodnika pod kątem prostym ( mi Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru ( =0).
Dlatego mi Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru (=0, co należało udowodnić. Zatem linie siły pola elektrostatycznego zbliżają się do powierzchni przewodnika pod kątem prostym ( mi Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru ( =0).
D  Aby udowodnić drugi warunek, weźmy dowolny punkt na granicy i otoczmy go nieskończenie płaską objętością w kształcie równoległościanu (ryc. 11.12) i zastosujmy do niego twierdzenie Gaussa w postaci całkowej
Aby udowodnić drugi warunek, weźmy dowolny punkt na granicy i otoczmy go nieskończenie płaską objętością w kształcie równoległościanu (ryc. 11.12) i zastosujmy do niego twierdzenie Gaussa w postaci całkowej  . Co ciekawe, przepływ wektorowy Ponieważ dolna powierzchnia znajduje się w ośrodku przewodzącym, strumień wektorowy przez nią przepływa Co ciekawe, przepływ wektorowy jest równa zeru, a także przez ściany boczne (te ściany są nieskończenie małe, dodatkowo wektor Co ciekawe, przepływ wektorowyślizga się po nich). Wektor przepływu
. Co ciekawe, przepływ wektorowy Ponieważ dolna powierzchnia znajduje się w ośrodku przewodzącym, strumień wektorowy przez nią przepływa Co ciekawe, przepływ wektorowy jest równa zeru, a także przez ściany boczne (te ściany są nieskończenie małe, dodatkowo wektor Co ciekawe, przepływ wektorowyślizga się po nich). Wektor przepływu  przez górną granicę jest równa Co ciekawe, przepływ wektorowy, ponieważ wektory jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory I
przez górną granicę jest równa Co ciekawe, przepływ wektorowy, ponieważ wektory jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory I  pokrywają się w kierunku. Wewnątrz powierzchni całkowania znajdują się jedynie ładunki indukowane, a ich liczba jest równa
pokrywają się w kierunku. Wewnątrz powierzchni całkowania znajdują się jedynie ładunki indukowane, a ich liczba jest równa  , Gdzie
, Gdzie 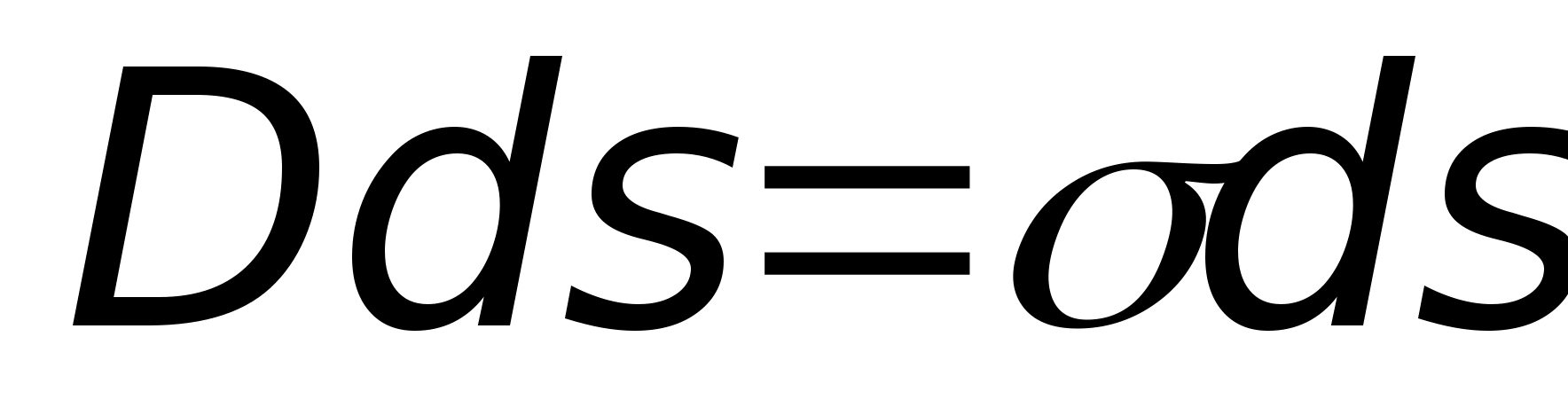 Lub
Lub  .
.
- gęstość powierzchniowa indukowanego ładunku. Następnie 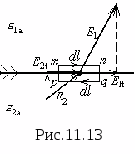 U warunki na styku dwóch różnych dielektryków. mi (mi Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów wspólnych dla dwóch różnych dielektryków składowe styczne wektora są równe pod względem wielkości mi 1 t = Co ciekawe, przepływ wektorowy
(Co ciekawe, przepływ wektorowy 2 t) i normalne składowe wektora 1n =D).
U warunki na styku dwóch różnych dielektryków. mi (mi Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów wspólnych dla dwóch różnych dielektryków składowe styczne wektora są równe pod względem wielkości mi 1 t = Co ciekawe, przepływ wektorowy
(Co ciekawe, przepływ wektorowy 2 t) i normalne składowe wektora 1n =D).
2n dłPokażmy zasadność pierwszego warunku, dla którego bierzemy dowolny punkt na styku dwóch różnych dielektryków i otaczamy go nieskończenie małą (długość - mnpq .
(ryc. 11.13) mi Stwórzmy wyrażenie na cyrkulację wektora wzdłuż tego konturu. Strona mn znajduje się w górnym środowisku i jeśli obrysujemy kontur zgodnie z ruchem wskazówek zegara, wówczas składowa cyrkulacji wzdłuż tej strony wynosi . To samo z boku pk mi znajduje się w drugim środowisku. W ostatnim wyrażeniu jest minus, ponieważ jest to składowa styczna dł 2t i wektor mi skierowane w przeciwne strony. Elementy obiegu wektorowego wzdłuż boków z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy po południu nq 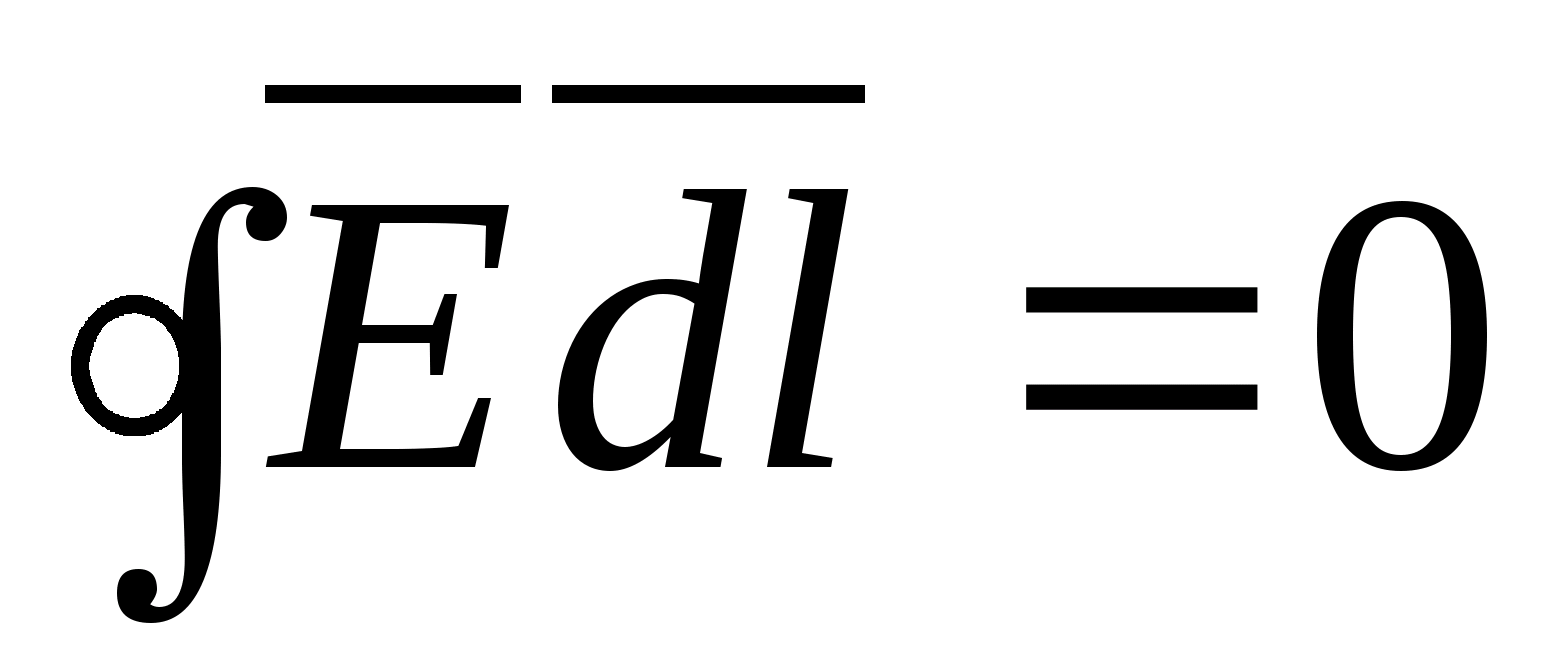 . Następnie
. Następnie 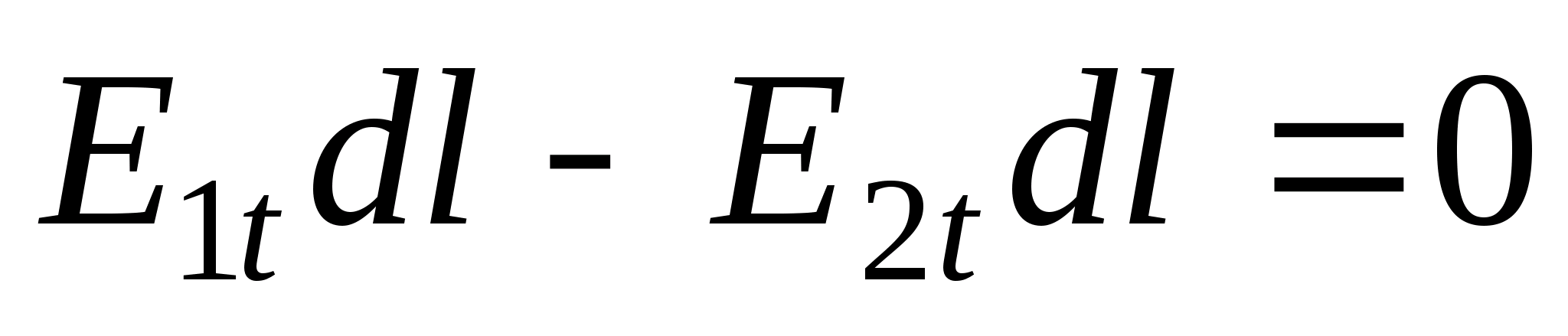 można pominąć ze względu na małą wielkość tych boków. Dla pola potencjalnego, które jest elektrostatyczne,
można pominąć ze względu na małą wielkość tych boków. Dla pola potencjalnego, które jest elektrostatyczne, 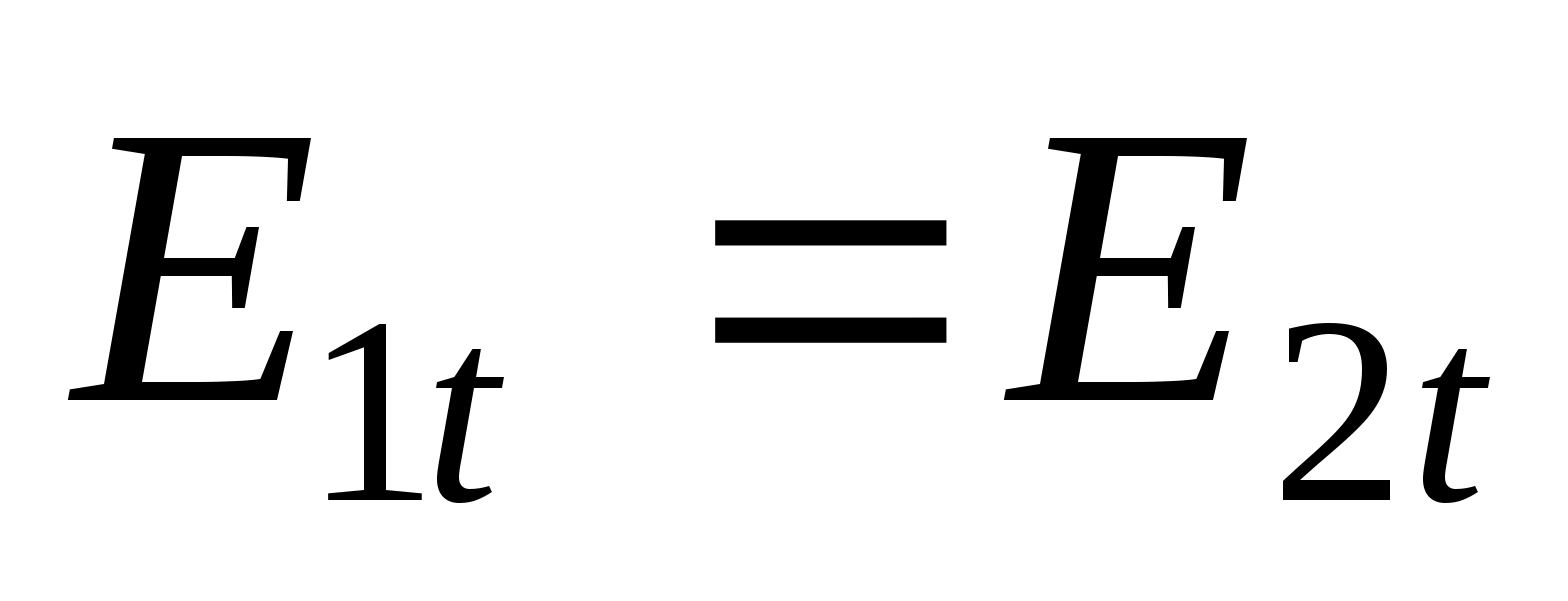 Lub
Lub
D 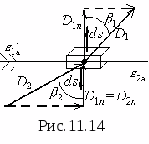 , co należało udowodnić. Co ciekawe, przepływ wektorowy Aby udowodnić drugi warunek, weźmy dowolny punkt na granicy i otoczmy go nieskończenie małą płaską objętością w kształcie równoległościanu (ryc. 11.14) i zastosujmy do niego twierdzenie Gaussa w postaci całkowej. Przez boczne ściany przepływu wektora
, co należało udowodnić. Co ciekawe, przepływ wektorowy Aby udowodnić drugi warunek, weźmy dowolny punkt na granicy i otoczmy go nieskończenie małą płaską objętością w kształcie równoległościanu (ryc. 11.14) i zastosujmy do niego twierdzenie Gaussa w postaci całkowej. Przez boczne ściany przepływu wektora 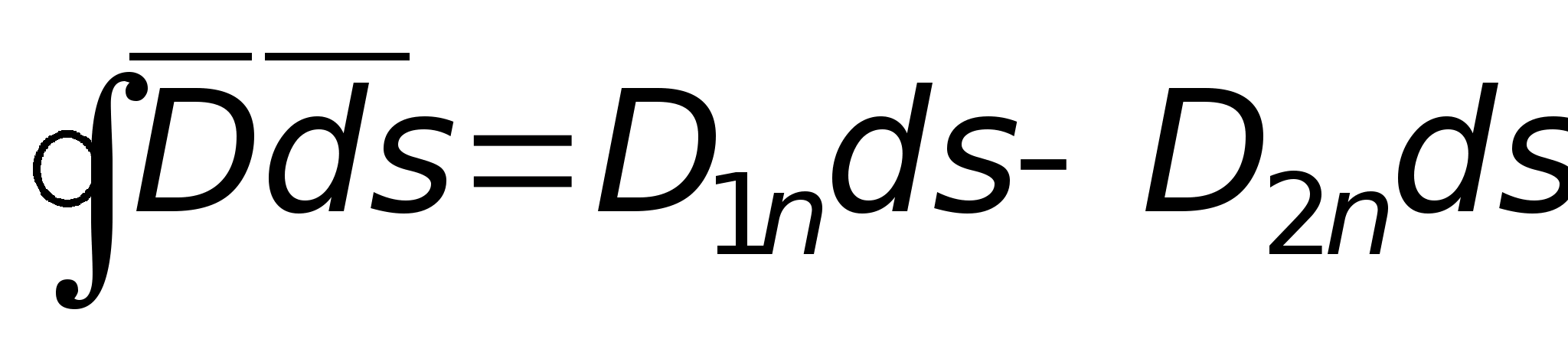 można pominąć ze względu na małość tych ścian, a także odpowiednio przez górną i dolną oraz . Stąd,
można pominąć ze względu na małość tych ścian, a także odpowiednio przez górną i dolną oraz . Stąd, 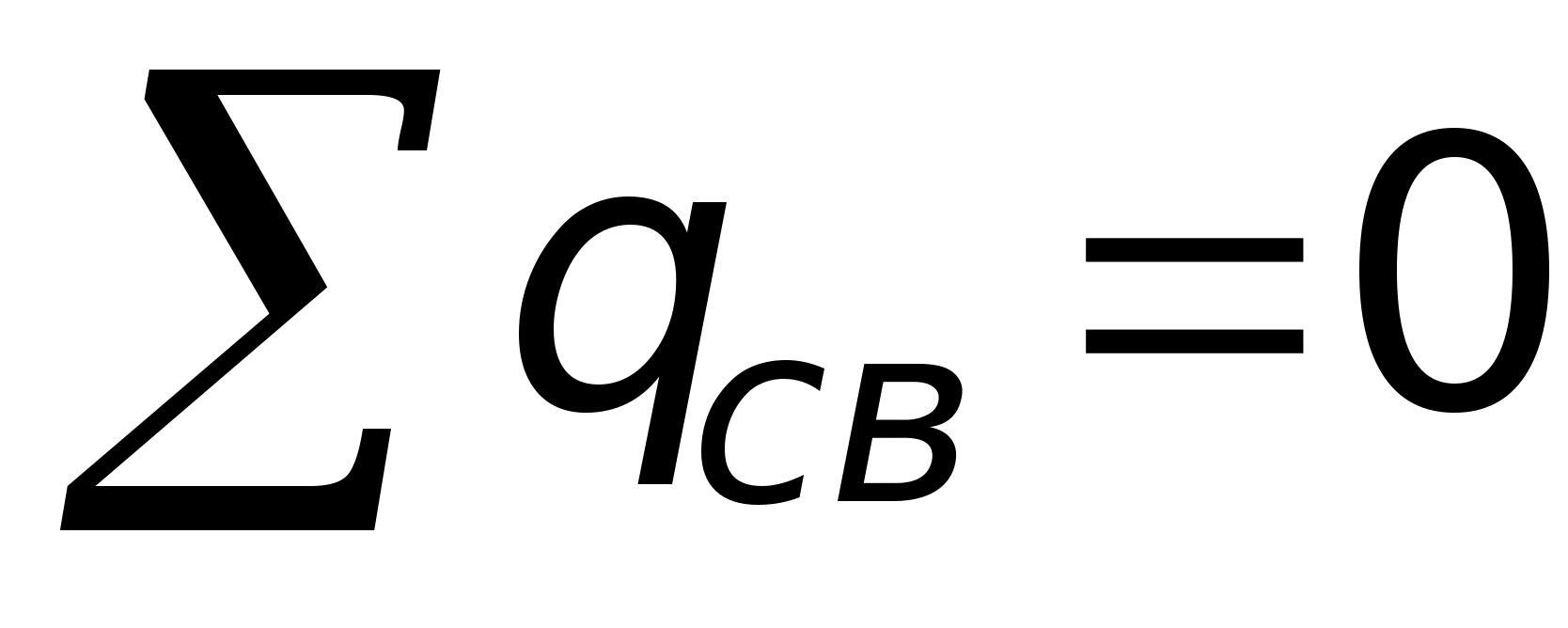 . W ramach przydzielonego wolumenu nie występują bezpłatne opłaty, tj.
. W ramach przydzielonego wolumenu nie występują bezpłatne opłaty, tj. 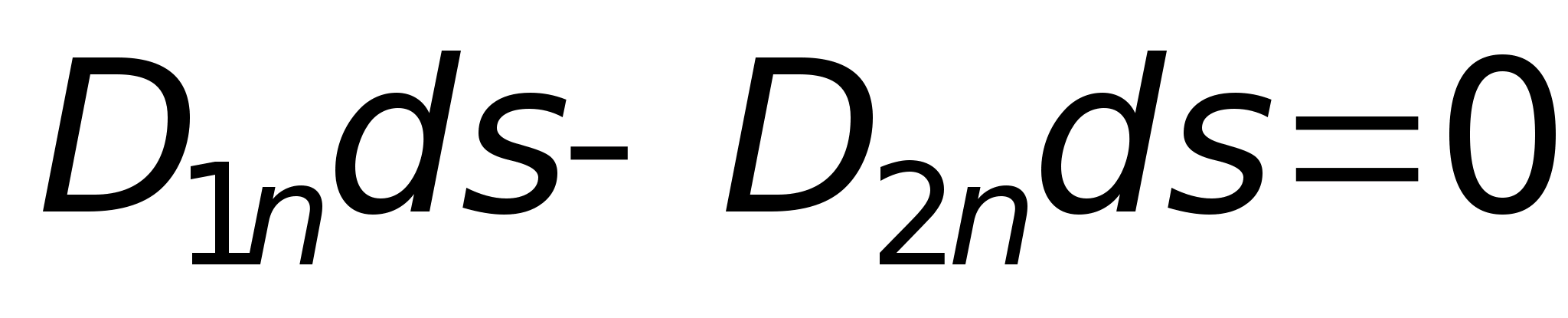 można pominąć ze względu na małą wielkość tych boków. Dla pola potencjalnego, które jest elektrostatyczne,
można pominąć ze względu na małą wielkość tych boków. Dla pola potencjalnego, które jest elektrostatyczne, 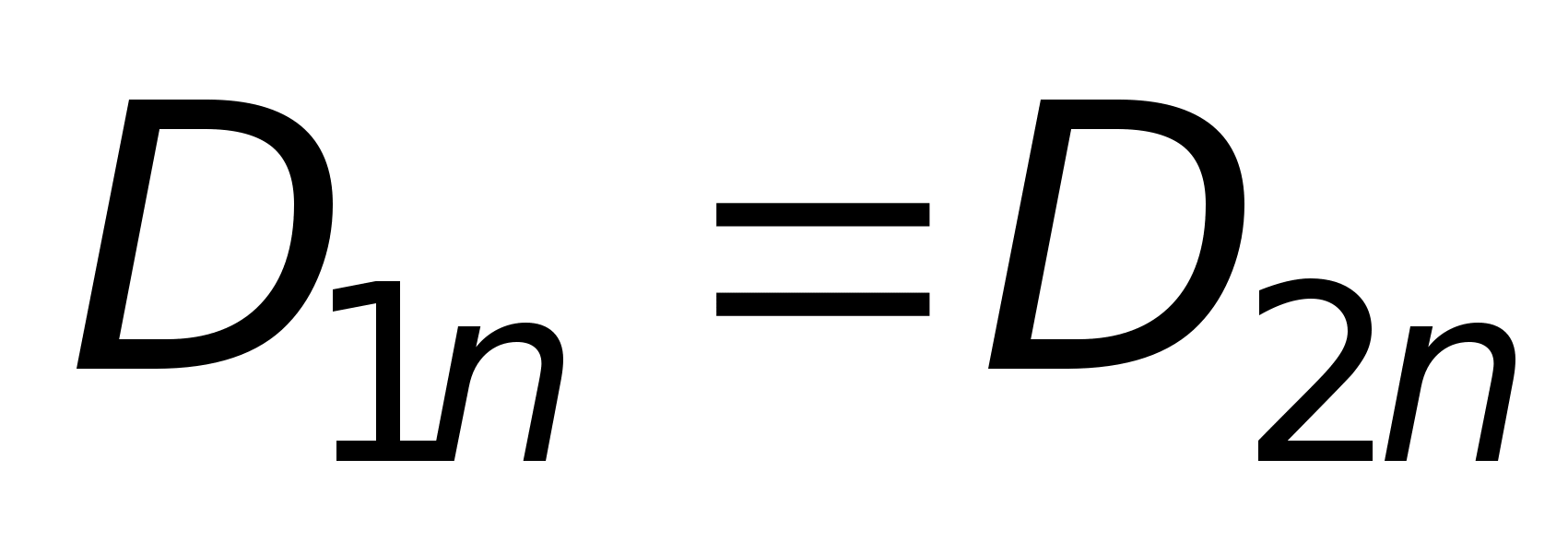 .
.  Lub
Lub 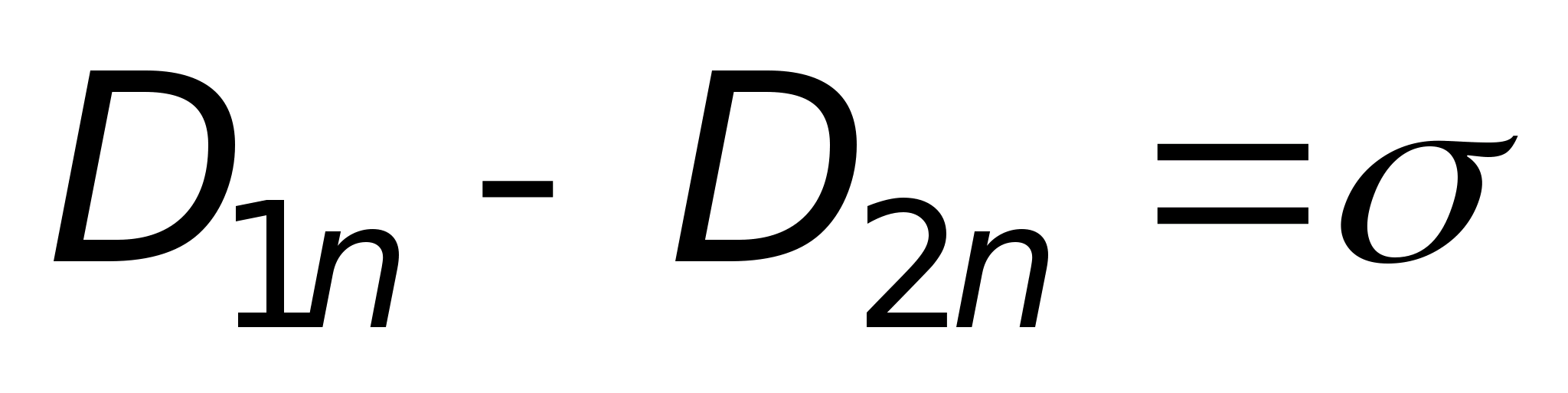 , tj. w obecności wolnych ładunków na granicy faz, składowa normalna wektora Co ciekawe, przepływ wektorowy ulega skokowi o wartość powierzchniowej gęstości swobodnego ładunku.
, tj. w obecności wolnych ładunków na granicy faz, składowa normalna wektora Co ciekawe, przepływ wektorowy ulega skokowi o wartość powierzchniowej gęstości swobodnego ładunku.
Pole elektrostatyczne naładowanej osi
Z  Naładowana oś to bardzo cienki, teoretycznie nieskończenie długi przewodnik, w którym znajduje się ładunek. Nie da się wskazać całego ładunku osi (jest on równy nieskończoności), dlatego wskazany jest ładunek liniowy
Naładowana oś to bardzo cienki, teoretycznie nieskończenie długi przewodnik, w którym znajduje się ładunek. Nie da się wskazać całego ładunku osi (jest on równy nieskończoności), dlatego wskazany jest ładunek liniowy 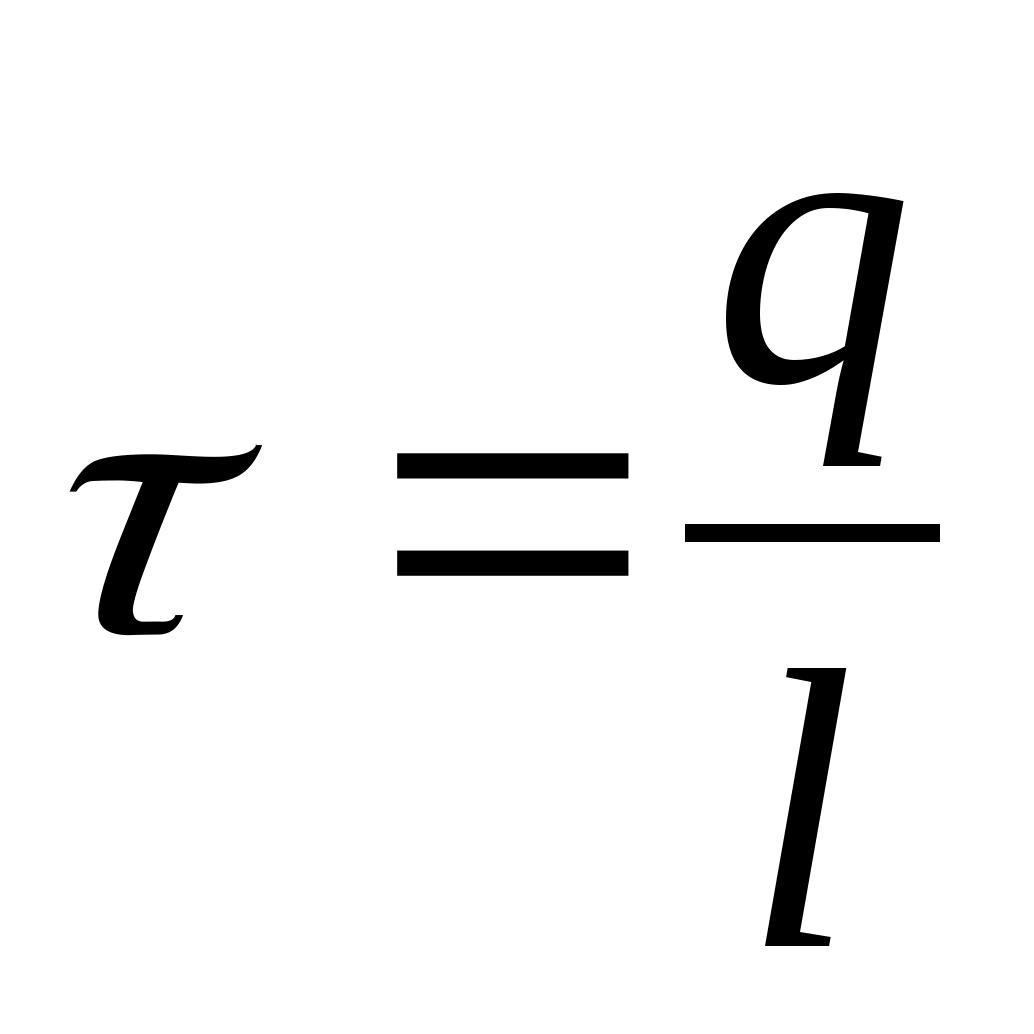 , tj. opłata za jednostkę długości osi. Niech oś będzie miała ładunek dodatni τ
znajduje się w przepuszczalnym środowisku ε
a (ryc. 11.15). Korzystając z całkowej postaci twierdzenia Gaussa, obliczymy natężenie pola w dowolnym punkcie położonym w pewnej odległości R od osi. W tym celu przeciągamy przez ten punkt zamkniętą powierzchnię w postaci walca o długości l. Wektor przepływu mi zachodzi tylko poprzez boczną powierzchnię tego cylindra,
ponieważ w punktach znajdujących się na jego dnie wektory mi I jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory są prostopadłe, a ich iloczyn wynosi zero. W punktach na powierzchni bocznej wektory mi z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory pokrywają się w kierunku, a ich iloczyn jest równy iloczynowi modułów i modułu mi jest taki sam we wszystkich tych punktach ze względu na symetrię. Biorąc pod uwagę powyższe, wewnątrz powierzchni całkowania mamy ładunek
, tj. opłata za jednostkę długości osi. Niech oś będzie miała ładunek dodatni τ
znajduje się w przepuszczalnym środowisku ε
a (ryc. 11.15). Korzystając z całkowej postaci twierdzenia Gaussa, obliczymy natężenie pola w dowolnym punkcie położonym w pewnej odległości R od osi. W tym celu przeciągamy przez ten punkt zamkniętą powierzchnię w postaci walca o długości l. Wektor przepływu mi zachodzi tylko poprzez boczną powierzchnię tego cylindra,
ponieważ w punktach znajdujących się na jego dnie wektory mi I jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory są prostopadłe, a ich iloczyn wynosi zero. W punktach na powierzchni bocznej wektory mi z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory pokrywają się w kierunku, a ich iloczyn jest równy iloczynowi modułów i modułu mi jest taki sam we wszystkich tych punktach ze względu na symetrię. Biorąc pod uwagę powyższe, wewnątrz powierzchni całkowania mamy ładunek 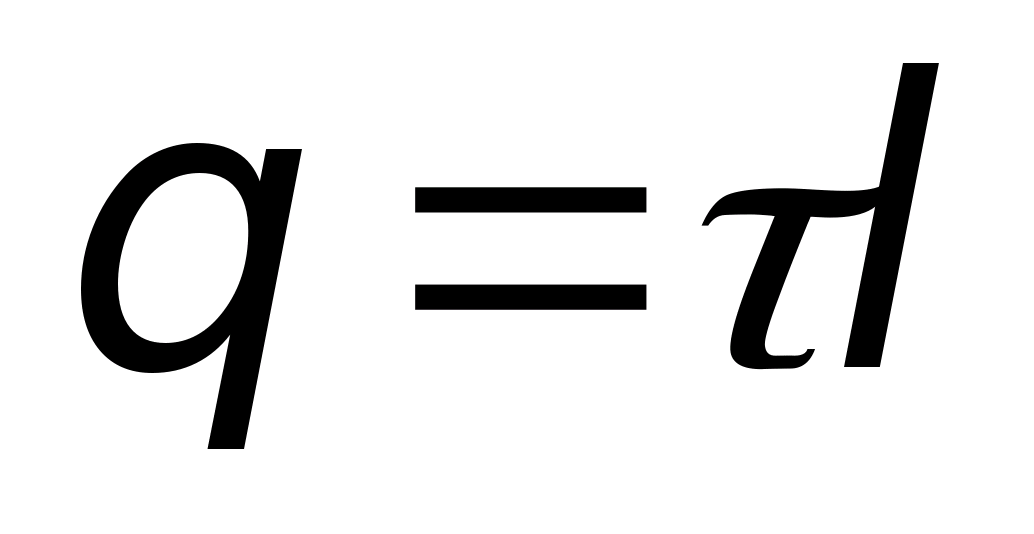 . Dlatego
. Dlatego 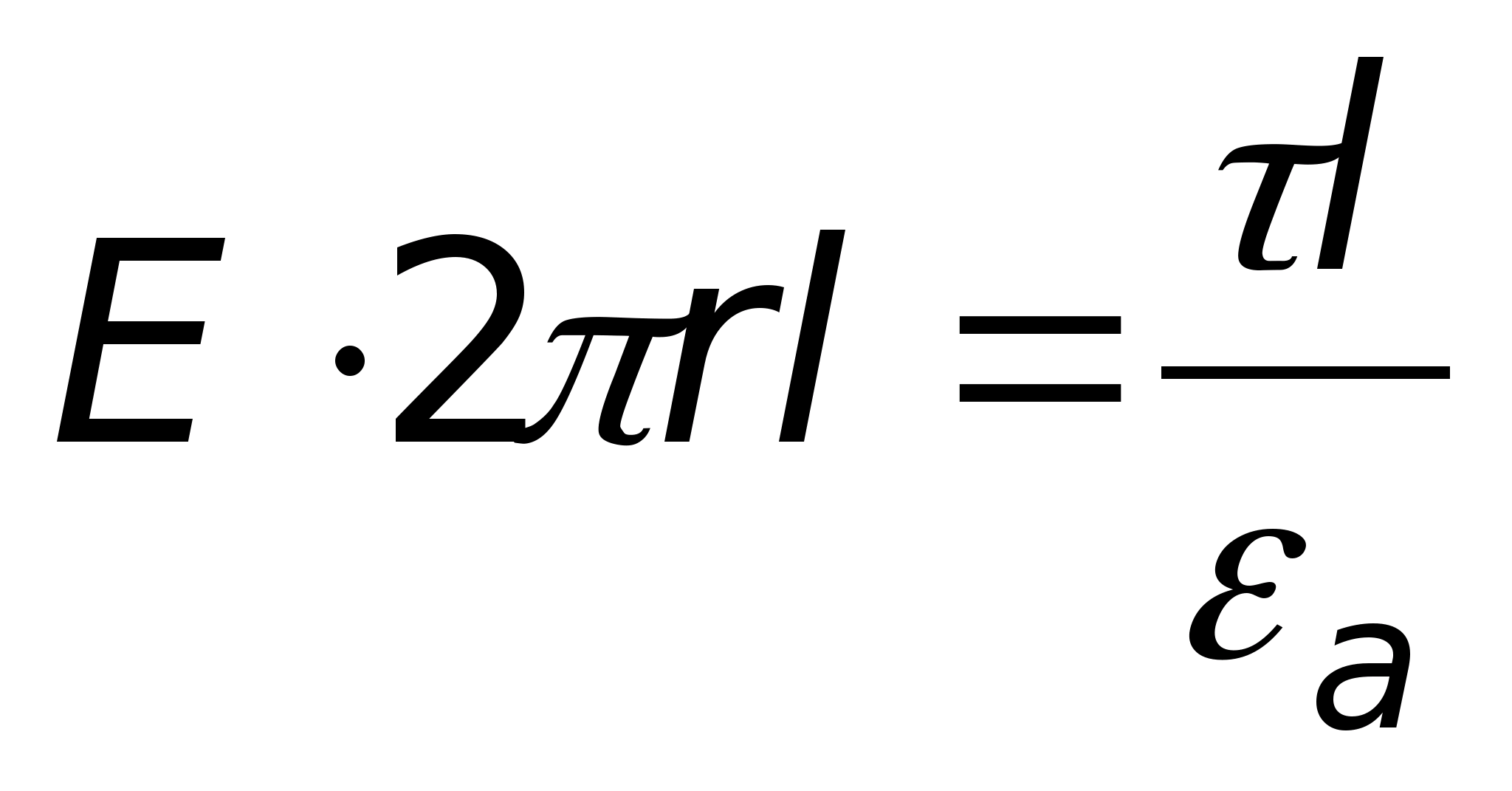 można pominąć ze względu na małą wielkość tych boków. Dla pola potencjalnego, które jest elektrostatyczne,
można pominąć ze względu na małą wielkość tych boków. Dla pola potencjalnego, które jest elektrostatyczne, 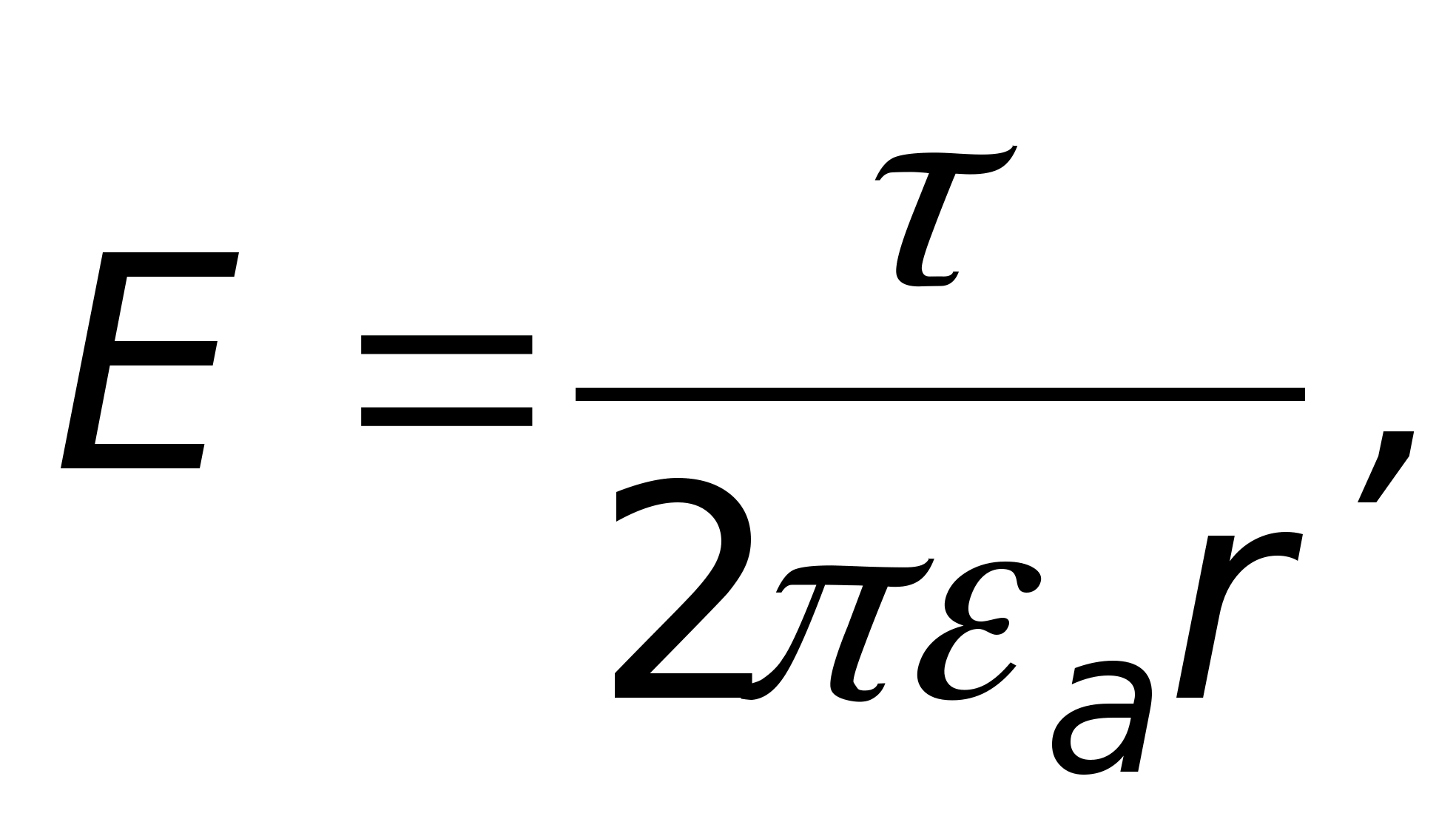 te. siła w danym polu zmienia się odwrotnie proporcjonalnie do odległości od osi.
te. siła w danym polu zmienia się odwrotnie proporcjonalnie do odległości od osi.
Potencjalna stała całkowania A zależy od tego, gdzie zlokalizować punkt o potencjale zerowym. W konsekwencji w danym polu potencjał zmienia się zgodnie z prawem logarytmicznym.
Pole elektrostatyczne dwóch naładowanych osi
N 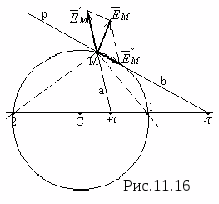 W praktyce najczęściej dwie naładowane osie niosą ładunki o jednakowej wielkości i przeciwnym znaku + E ds l rτ
I - τ
. Dokładnie to rozważymy (ryc. 11.16). Weźmy dowolny punkt w polu M, którego położenie będzie charakteryzowane przez odległość A do dodatniej osi i odległości B do osi ujemnej i przede wszystkim obliczyć w niej natężenie pola metodą superpozycji:
W praktyce najczęściej dwie naładowane osie niosą ładunki o jednakowej wielkości i przeciwnym znaku + E ds l rτ
I - τ
. Dokładnie to rozważymy (ryc. 11.16). Weźmy dowolny punkt w polu M, którego położenie będzie charakteryzowane przez odległość A do dodatniej osi i odległości B do osi ujemnej i przede wszystkim obliczyć w niej natężenie pola metodą superpozycji: 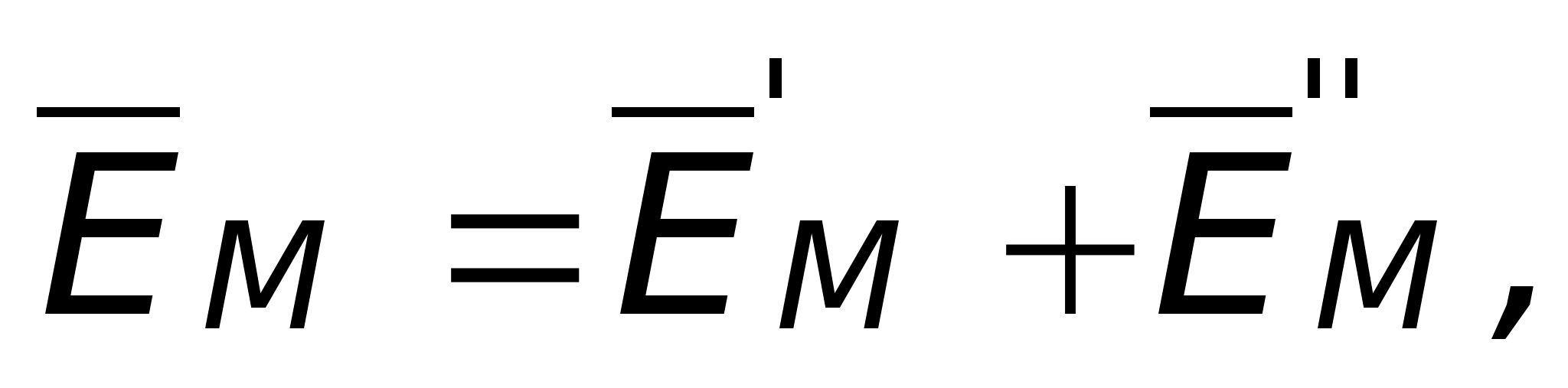 Gdzie
Gdzie  - składowe utworzone odpowiednio przez oś naładowaną dodatnio i ujemnie. Wartości tych składników można wyznaczyć korzystając ze wzorów zaczerpniętych z poprzedniego tematu, a mianowicie:
- składowe utworzone odpowiednio przez oś naładowaną dodatnio i ujemnie. Wartości tych składników można wyznaczyć korzystając ze wzorów zaczerpniętych z poprzedniego tematu, a mianowicie: 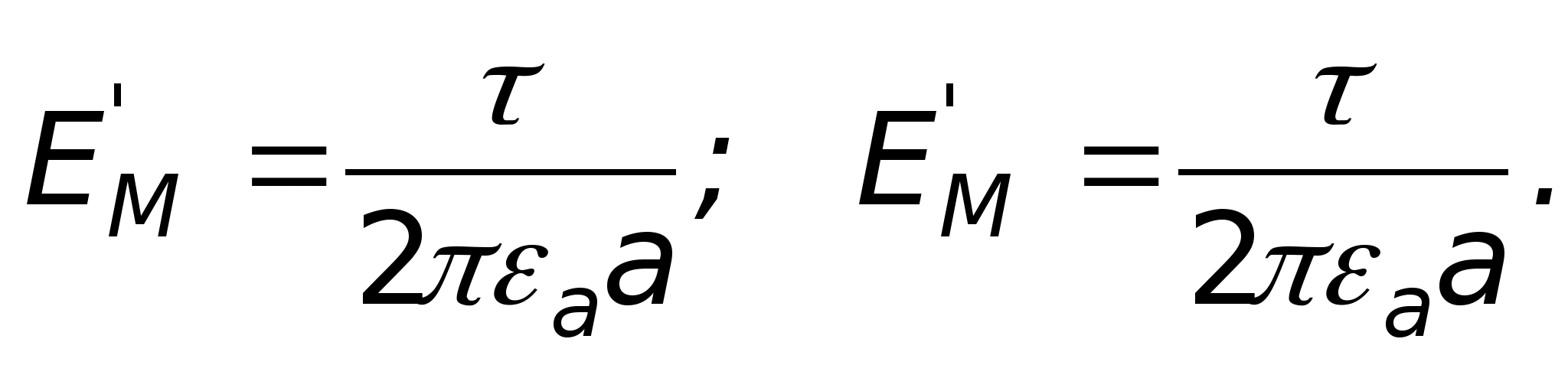 Podobnie dla potencjału
Podobnie dla potencjału 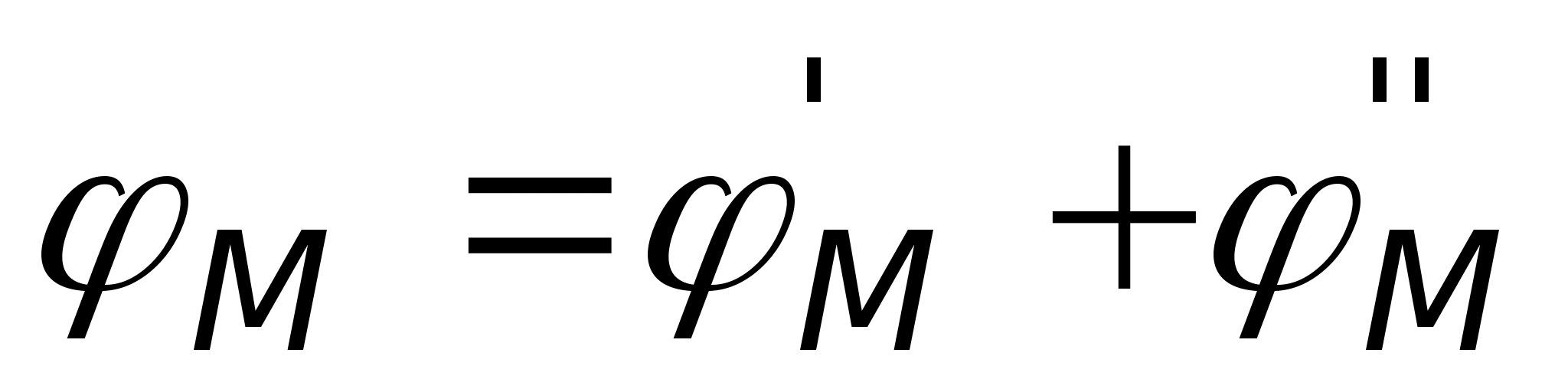 , Gdzie . Następnie Z ostatniego wyrażenia wynika, że zbiór punktów dla których
, Gdzie . Następnie Z ostatniego wyrażenia wynika, że zbiór punktów dla których  , reprezentuje ekwipotencjał. Z geometrii wiadomo, że miejscem punktów, czyli stosunkiem odległości, z których do dwóch danych punktów jest wartość stała, jest okrąg (twierdzenie Apoloniusza). Dlatego ekwipotencjały w polu dwóch naładowanych osi są okręgami. Konstruowanie linii ekwipotencjalnej przechodzącej przez punkt M, narysuj dwusieczne części wewnętrznej jestemB n zewnętrzne pMa rogi Punkty przecięcia tych dwusiecznych z linią poprowadzoną przez osie (t.1 i t.2), a także t. M są trzema punktami tego ekwipotencjału. Środek tego okręgu znajduje się w punkcie położonym w połowie odległości między punktami 1 i 2.
, reprezentuje ekwipotencjał. Z geometrii wiadomo, że miejscem punktów, czyli stosunkiem odległości, z których do dwóch danych punktów jest wartość stała, jest okrąg (twierdzenie Apoloniusza). Dlatego ekwipotencjały w polu dwóch naładowanych osi są okręgami. Konstruowanie linii ekwipotencjalnej przechodzącej przez punkt M, narysuj dwusieczne części wewnętrznej jestemB n zewnętrzne pMa rogi Punkty przecięcia tych dwusiecznych z linią poprowadzoną przez osie (t.1 i t.2), a także t. M są trzema punktami tego ekwipotencjału. Środek tego okręgu znajduje się w punkcie położonym w połowie odległości między punktami 1 i 2.
Pole elektrostatyczne i pojemność dwuprzewodowej linii elektroenergetycznej (PTL)
P 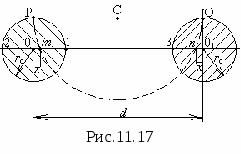 Mimo że przewody linii energetycznej mają ten sam promień R O ,
położony w pewnej odległości D od siebie i znajdują się w ośrodku o przepuszczalności ε a (ryc. 11.17). τ
Jeśli lewy przewód jest naładowany τ
na jednostkę długości, w prawo - mi, wówczas w przestrzeni między drutami powstanie pole elektrostatyczne, które można przedstawić jako część pola dwóch naładowanych osi. Rzeczywiście, ponieważ druty są metalowe, nie ma w nich pola ( =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw M I N, =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw M stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. N =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw I stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. ustaw je tak, aby powierzchnie przewodów były dla nich ekwipotencjalne. Zwrotnica nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych ( X nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych () ze względu na symetrię jest taka sama w lewym i prawym przewodzie. Aby określić wartość =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw M stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest..
Mimo że przewody linii energetycznej mają ten sam promień R O ,
położony w pewnej odległości D od siebie i znajdują się w ośrodku o przepuszczalności ε a (ryc. 11.17). τ
Jeśli lewy przewód jest naładowany τ
na jednostkę długości, w prawo - mi, wówczas w przestrzeni między drutami powstanie pole elektrostatyczne, które można przedstawić jako część pola dwóch naładowanych osi. Rzeczywiście, ponieważ druty są metalowe, nie ma w nich pola ( =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw M I N, =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw M stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. N =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw I stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. ustaw je tak, aby powierzchnie przewodów były dla nich ekwipotencjalne. Zwrotnica nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych ( X nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych () ze względu na symetrię jest taka sama w lewym i prawym przewodzie. Aby określić wartość =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw M stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest..
Weźmy punkty 1 i 2 i zapiszmy wyrażenia na potencjały tych punktów w polu dwóch naładowanych osi znajdujących się w punkcie. 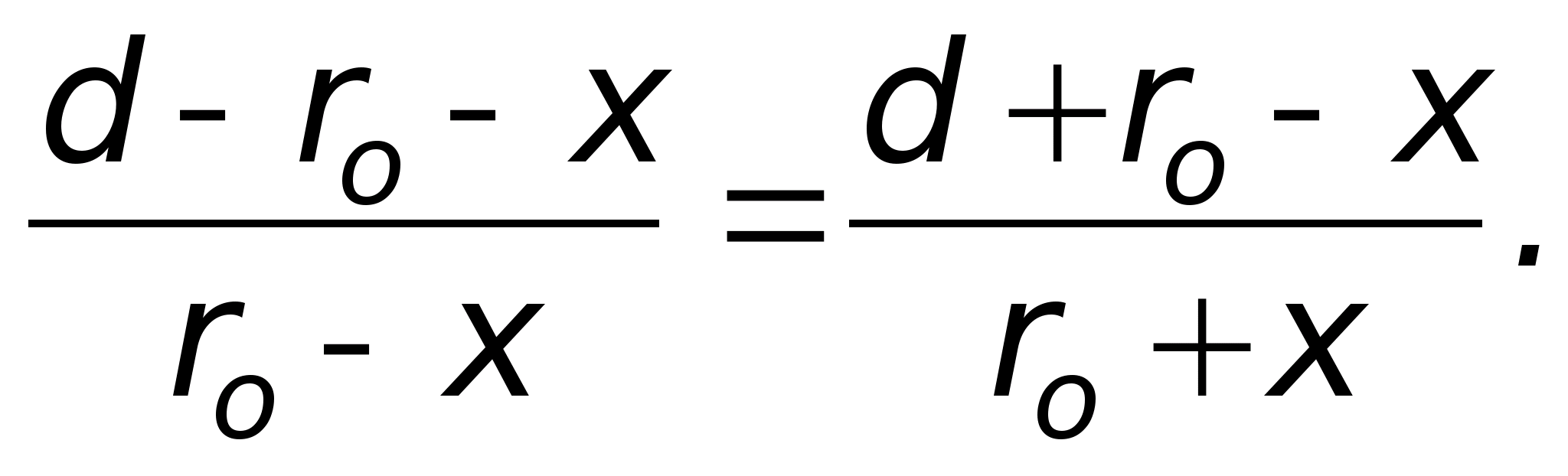 Ponieważ punkty 1 i 2 znajdują się na powierzchni tego samego drutu, zatem φ 1 = φ 2 nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych ( Rozwiązanie tej równości dla
Ponieważ punkty 1 i 2 znajdują się na powierzchni tego samego drutu, zatem φ 1 = φ 2 nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych ( Rozwiązanie tej równości dla 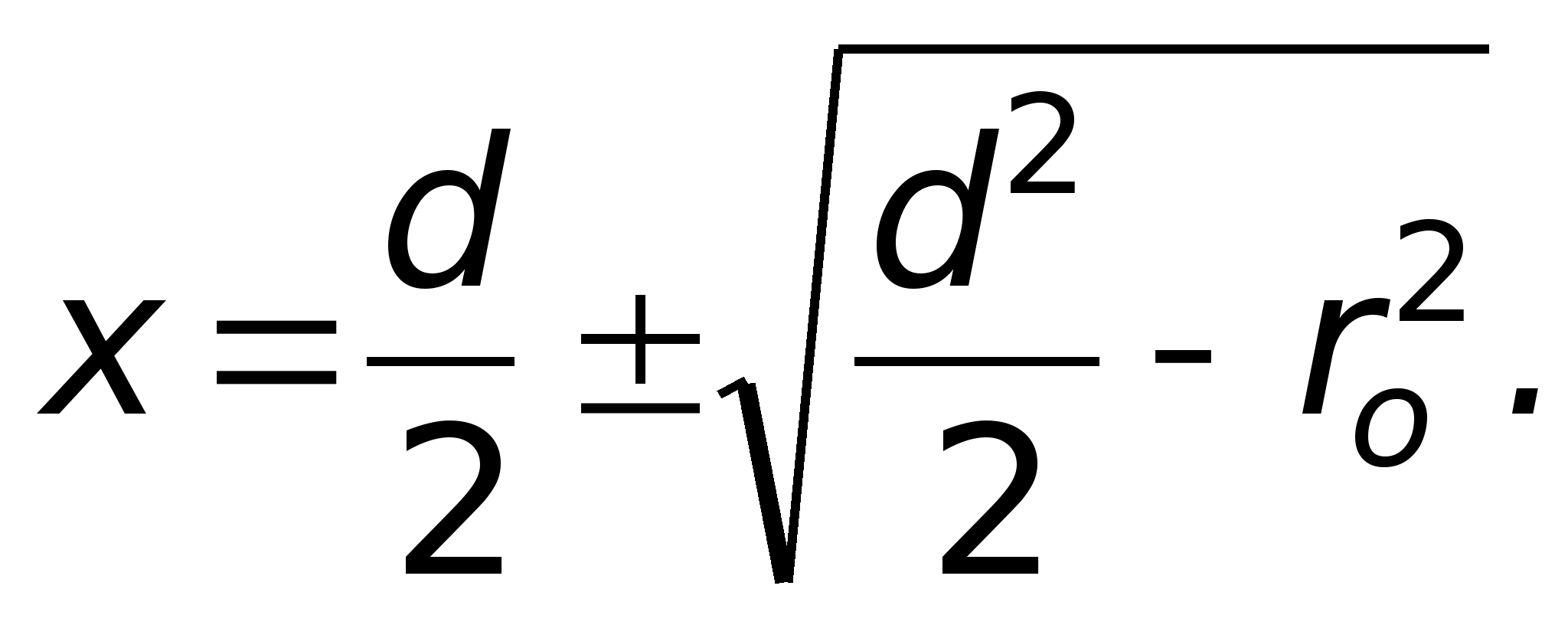 , otrzymujemy nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych ( W tym wyrażeniu podczas liczenia stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. od t.O plus określa położenie t. =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw, a minus to pozycja t. . Jeśli o d >> r nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych ( 1 =0,
nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych ( 2 =D, To nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych ( nie są obliczane przy użyciu wzoru otrzymanego powyżej, ale są obliczane graficznie. Aby to zrobić, narysuj wspólną styczną do powierzchni przewodników, podziel odległość między punktami styku (P i Q) na pół (t. C) i narysuj łuk okręgu przechodzącego przez punkty P i Q i mającego środek w t. C. Punkty przecięcia tego okręgu z linią O 1 O wyznaczają położenie osi elektrycznych. Z geometrycznej definicji położenia osi elektrycznych wynika również, że kiedy . Jeśli o T. M I stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. połączy się z t. O i O 1.
, otrzymujemy nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych ( W tym wyrażeniu podczas liczenia stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. od t.O plus określa położenie t. =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw, a minus to pozycja t. . Jeśli o d >> r nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych ( 1 =0,
nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych ( 2 =D, To nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych ( nie są obliczane przy użyciu wzoru otrzymanego powyżej, ale są obliczane graficznie. Aby to zrobić, narysuj wspólną styczną do powierzchni przewodników, podziel odległość między punktami styku (P i Q) na pół (t. C) i narysuj łuk okręgu przechodzącego przez punkty P i Q i mającego środek w t. C. Punkty przecięcia tego okręgu z linią O 1 O wyznaczają położenie osi elektrycznych. Z geometrycznej definicji położenia osi elektrycznych wynika również, że kiedy . Jeśli o T. M I stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. połączy się z t. O i O 1.
Po określeniu przemieszczenia osi problem zostaje zredukowany do poprzedniego.
Przejdźmy do kwestii przepustowości linii dwuprzewodowej. Jeżeli dwa przewodniki oddzielone są dielektrykiem i przenoszą ładunki o tej samej wartości i przeciwnym znaku, wówczas w przestrzeni pomiędzy nimi powstaje pole elektrostatyczne. Niech napięcie między przewodnikami będzie U. Następnie pojemność między przewodnikami jest stosunkiem wartości bezwzględnej ładunku na jednym z ciał do napięcia między nimi: 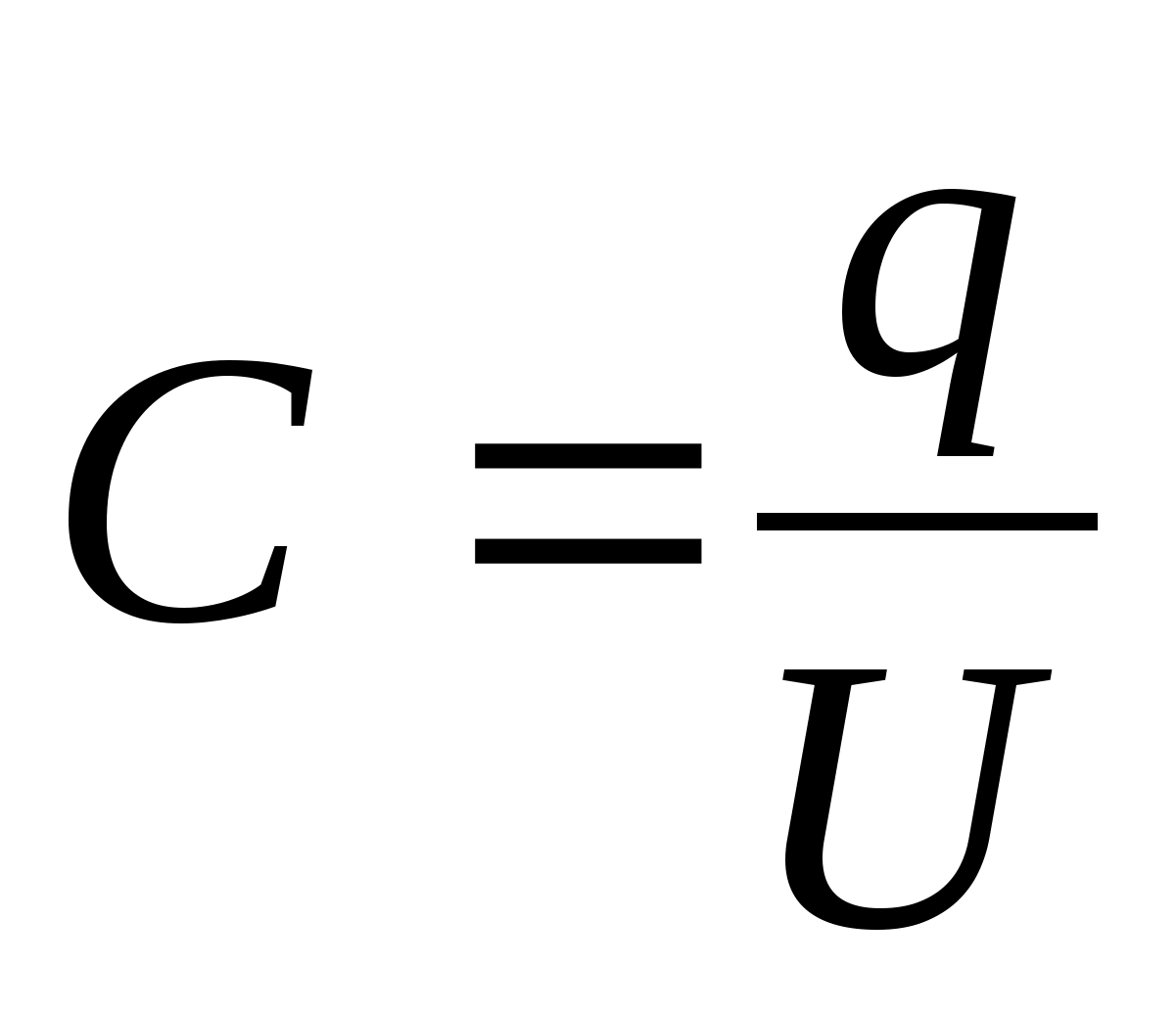 . Jednostką miary pojemności jest farad (
. Jednostką miary pojemności jest farad ( 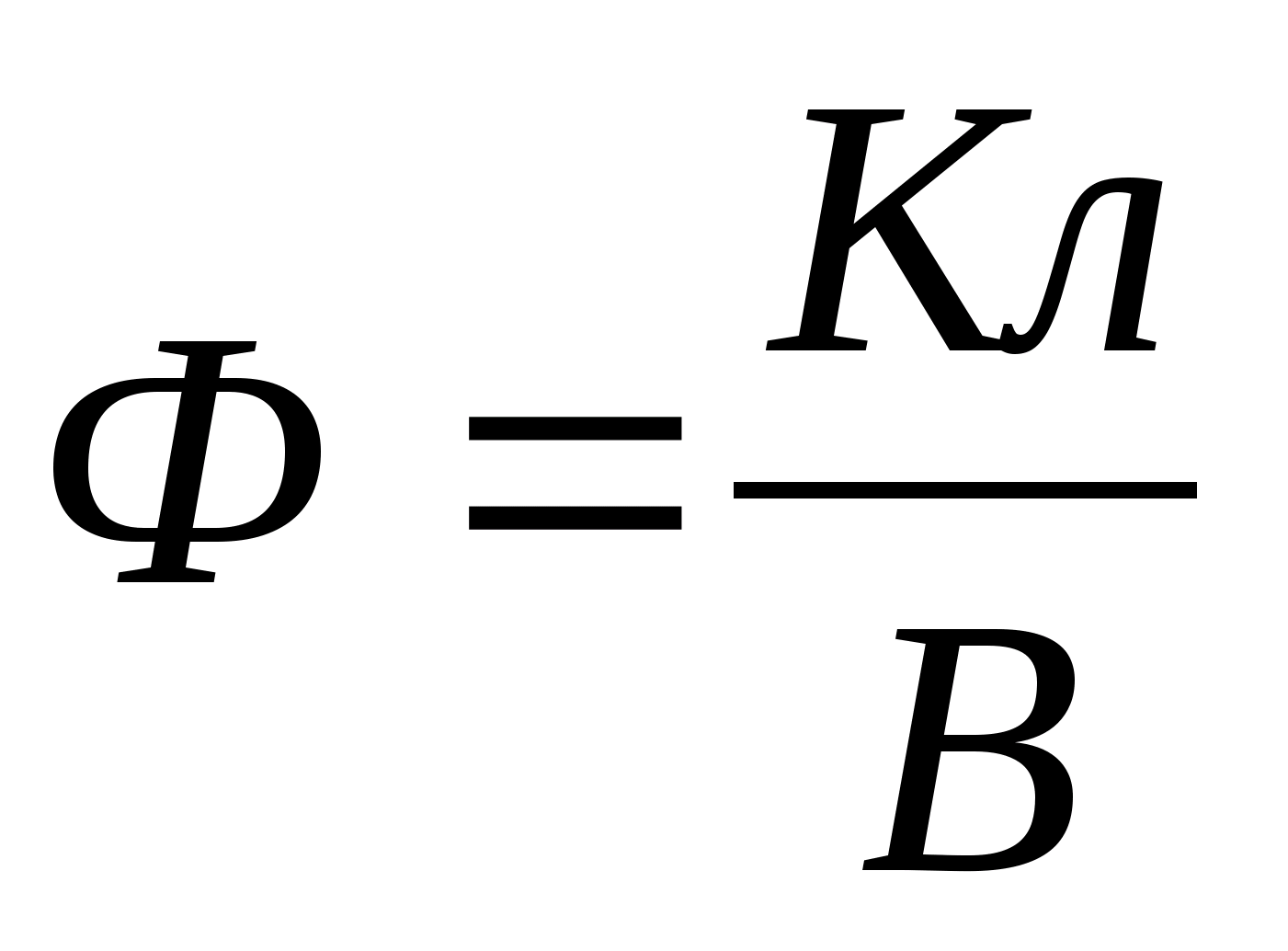 ). Ponieważ napięcie między ciałami jest proporcjonalne do znajdującego się na nich ładunku, pojemność nie zależy ani od ładunku, ani od napięcia, ale raczej od konfiguracji i wymiarów geometrycznych ciał, ich względnego położenia oraz właściwości dielektryka w w których się znajdują. Istnieją urządzenia zaprojektowane w celu uzyskania określonej pojemności - są to kondensatory, ale nie tylko kondensatory mają pojemność, ale dowolne dwa ciała zdolne do przenoszenia ładunków o tej samej wielkości i przeciwnym znaku.
). Ponieważ napięcie między ciałami jest proporcjonalne do znajdującego się na nich ładunku, pojemność nie zależy ani od ładunku, ani od napięcia, ale raczej od konfiguracji i wymiarów geometrycznych ciał, ich względnego położenia oraz właściwości dielektryka w w których się znajdują. Istnieją urządzenia zaprojektowane w celu uzyskania określonej pojemności - są to kondensatory, ale nie tylko kondensatory mają pojemność, ale dowolne dwa ciała zdolne do przenoszenia ładunków o tej samej wielkości i przeciwnym znaku.
Określmy pojemność linii dwuprzewodowej. Napięcie między przewodami Ładunek jednego z przewodów q=τl. Następnie 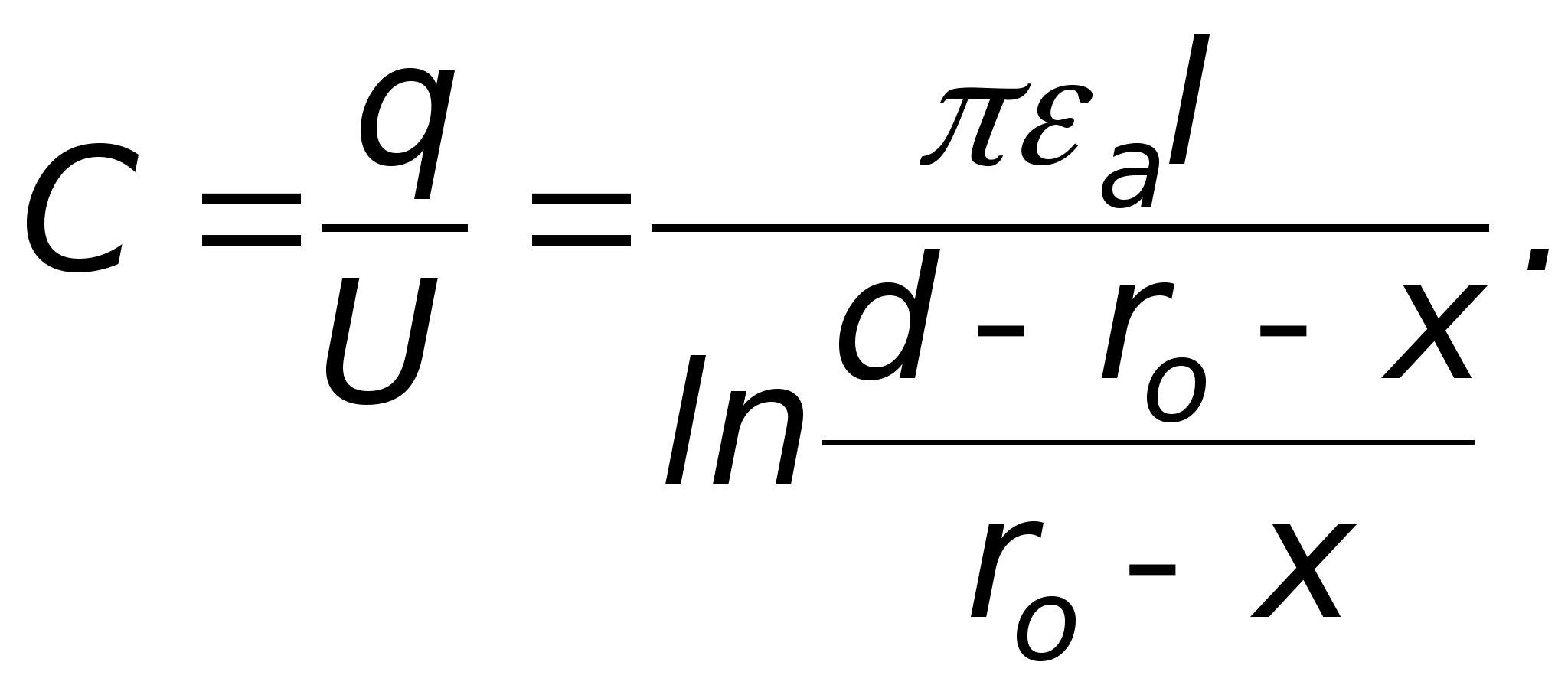 Często określa się pojemność na jednostkę długości linii
Często określa się pojemność na jednostkę długości linii 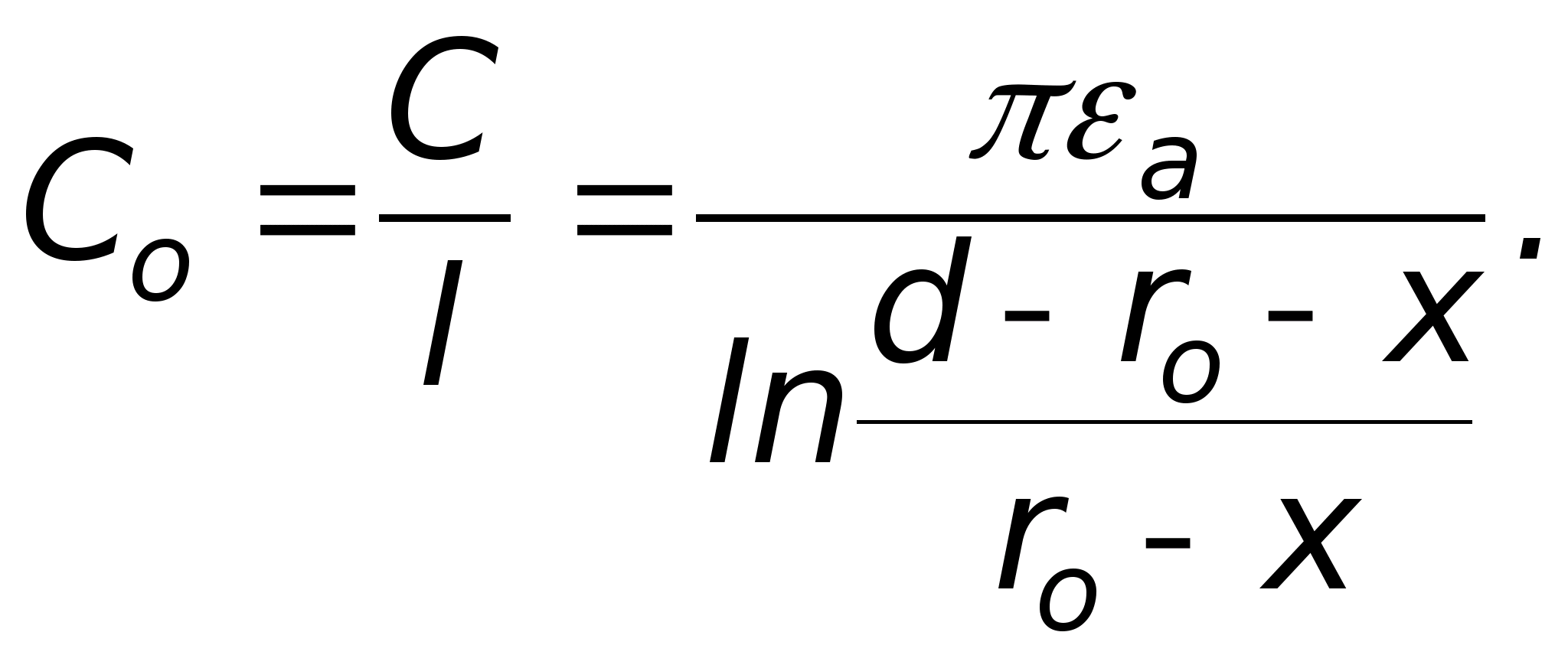 A co jeśli . Jeśli o, w takim razie nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych (=0 i
A co jeśli . Jeśli o, w takim razie nazywane są zwykle osiami elektrycznymi w przeciwieństwie do osi geometrycznych (punkty O i O 1). Przemieszczenie osi elektrycznych i geometrycznych (=0 i 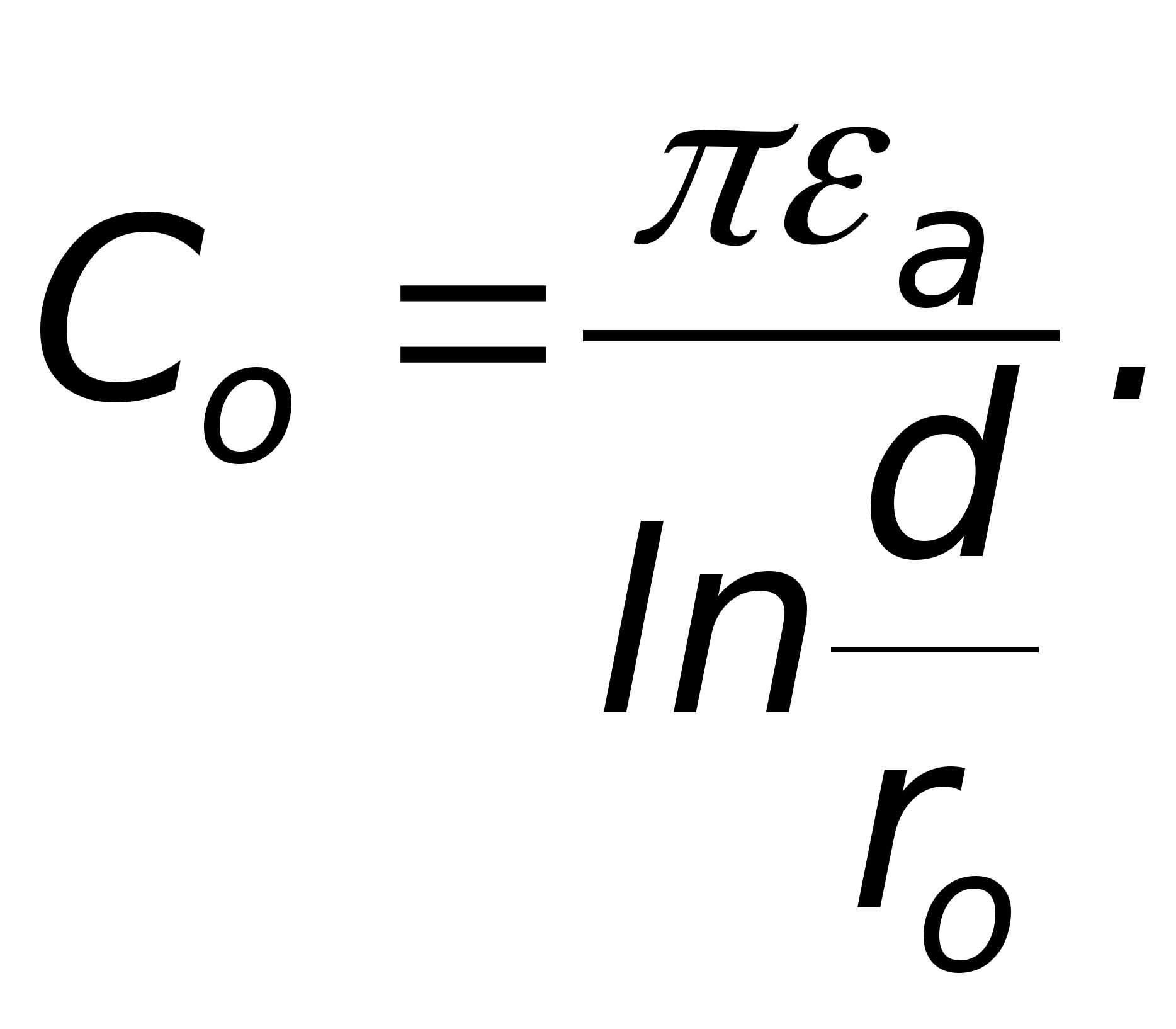 Z uzyskanych wzorów jasno wynika, że pojemność naprawdę zależy od wielkości linii i właściwości ośrodka, w którym znajdują się przewody, w szczególności jeśli odległość zostanie zwiększona D pomiędzy przewodami pojemność będzie się zmniejszać.
Z uzyskanych wzorów jasno wynika, że pojemność naprawdę zależy od wielkości linii i właściwości ośrodka, w którym znajdują się przewody, w szczególności jeśli odległość zostanie zwiększona D pomiędzy przewodami pojemność będzie się zmniejszać.
Pole elektrostatyczne i pojemność kabla koncentrycznego
DO  kabel oosiowy składa się z dwóch metalowych cylindrów współosiowych umieszczonych jeden w drugim i odizolowanych od siebie dielektrykiem o przepuszczalności ε
A(ryc. 11.18). Kabel ten jest szeroko stosowany przy wysokich częstotliwościach. Niech wewnętrzny cylinder, zwany żyłą, niesie ładunek + τ
i cylinder zewnętrzny (skorupa) – ładunek – τ
. Powstanie wówczas pole elektrostatyczne, które obliczymy dla poszczególnych obszarów kabla. Wewnątrz rdzenia (0> r>r 1) nie ma pola, ponieważ rdzeń przewodzi, tj. mi=0,
φ
=stała. Aby określić natężenie pola w przestrzeni pomiędzy rdzeniem a powłoką, korzystamy z twierdzenia Gaussa:
kabel oosiowy składa się z dwóch metalowych cylindrów współosiowych umieszczonych jeden w drugim i odizolowanych od siebie dielektrykiem o przepuszczalności ε
A(ryc. 11.18). Kabel ten jest szeroko stosowany przy wysokich częstotliwościach. Niech wewnętrzny cylinder, zwany żyłą, niesie ładunek + τ
i cylinder zewnętrzny (skorupa) – ładunek – τ
. Powstanie wówczas pole elektrostatyczne, które obliczymy dla poszczególnych obszarów kabla. Wewnątrz rdzenia (0> r>r 1) nie ma pola, ponieważ rdzeń przewodzi, tj. mi=0,
φ
=stała. Aby określić natężenie pola w przestrzeni pomiędzy rdzeniem a powłoką, korzystamy z twierdzenia Gaussa: 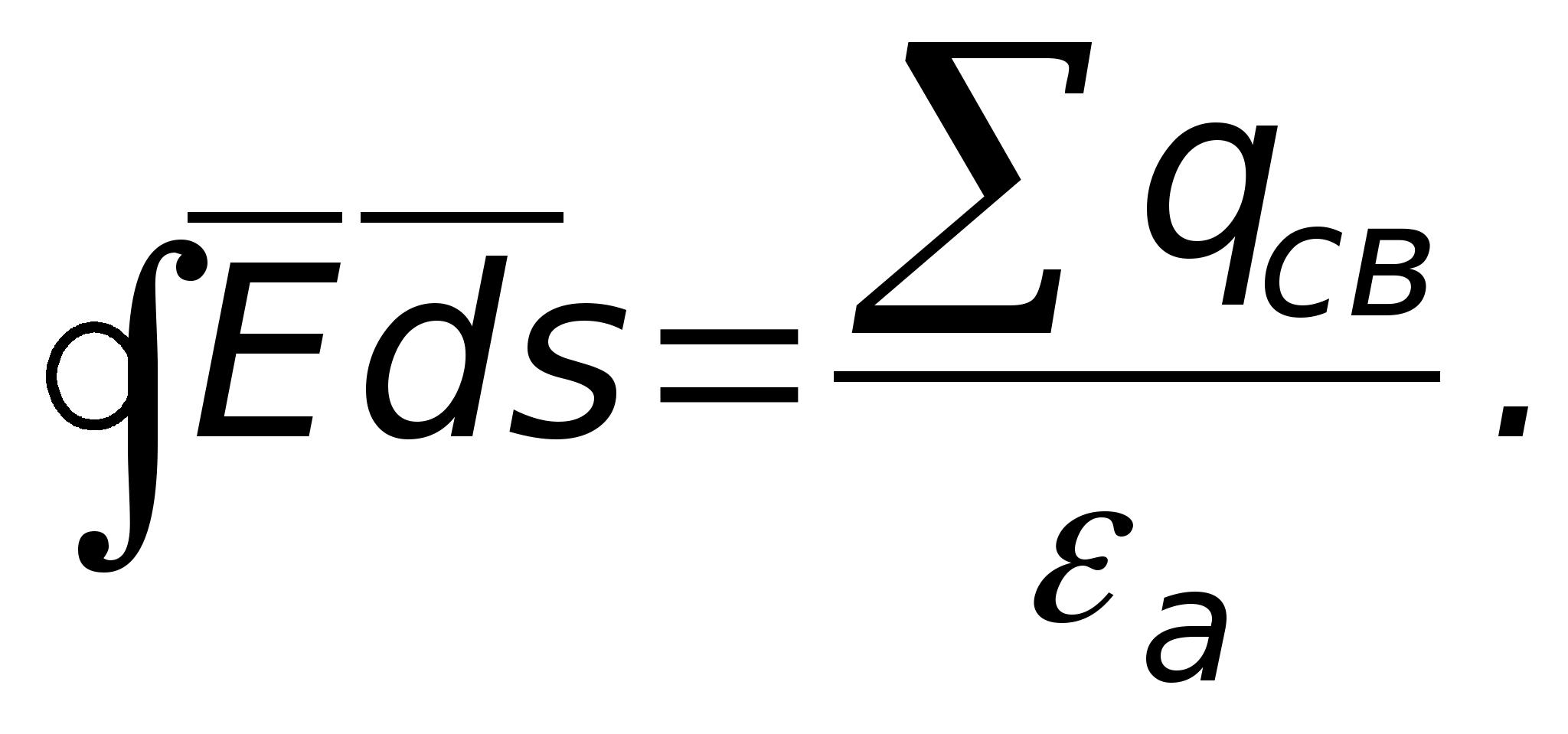 Jako powierzchnię całkowania przyjmujemy walec o promieniu R i długość l. Wektor przepływu mi przez dno tego cylindra jest równa zeru (wektory mi z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory prostopadle) i przez jego powierzchnię boczną
Jako powierzchnię całkowania przyjmujemy walec o promieniu R i długość l. Wektor przepływu mi przez dno tego cylindra jest równa zeru (wektory mi z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory prostopadle) i przez jego powierzchnię boczną 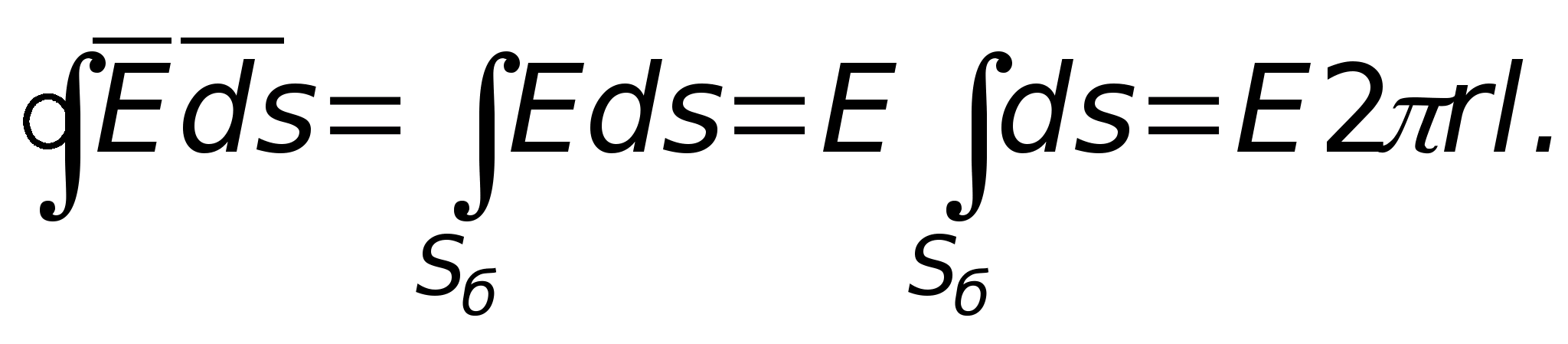
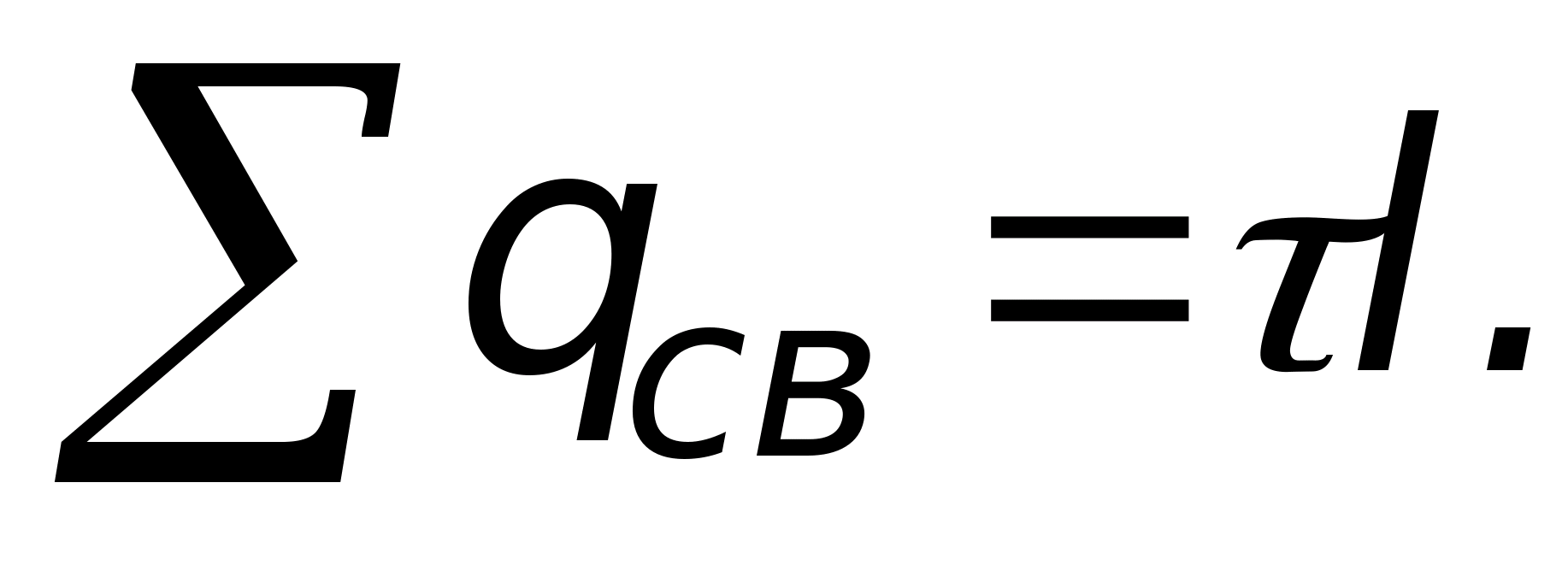 Następnie
Następnie 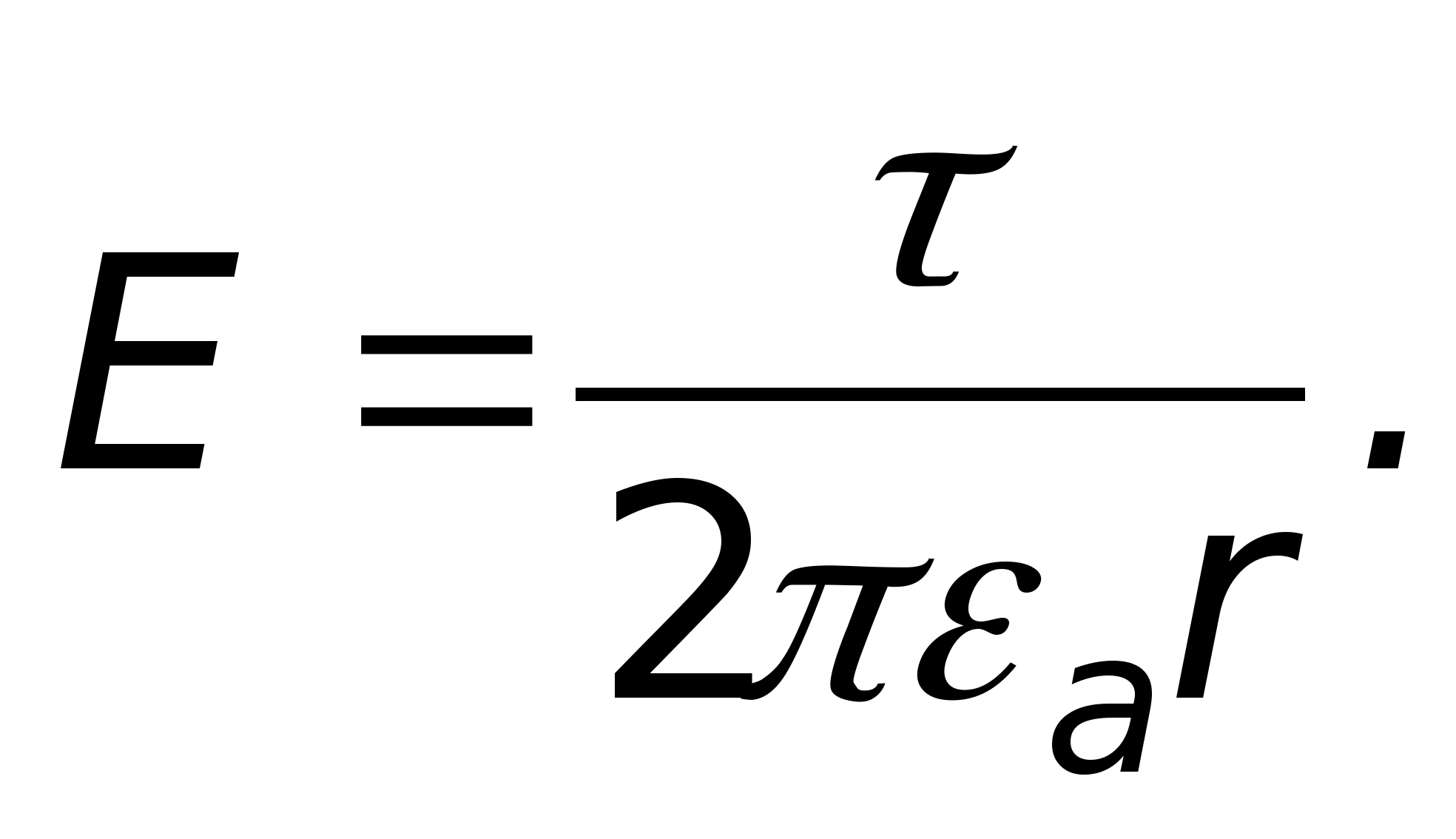 Ponieważ mi ma wtedy tylko składową promieniową
Ponieważ mi ma wtedy tylko składową promieniową
Do wszystkich punktów powłoki kabla ( R 2 3) mi=0, φ =const, ponieważ jest przewodzący. Na zewnątrz kabla ( R 3 Dlatego mi=0, φ =stała. Zatem w tym urządzeniu pole występuje tylko w przestrzeni pomiędzy rdzeniem a powłoką.
Pojemność kabla koncentrycznego Z=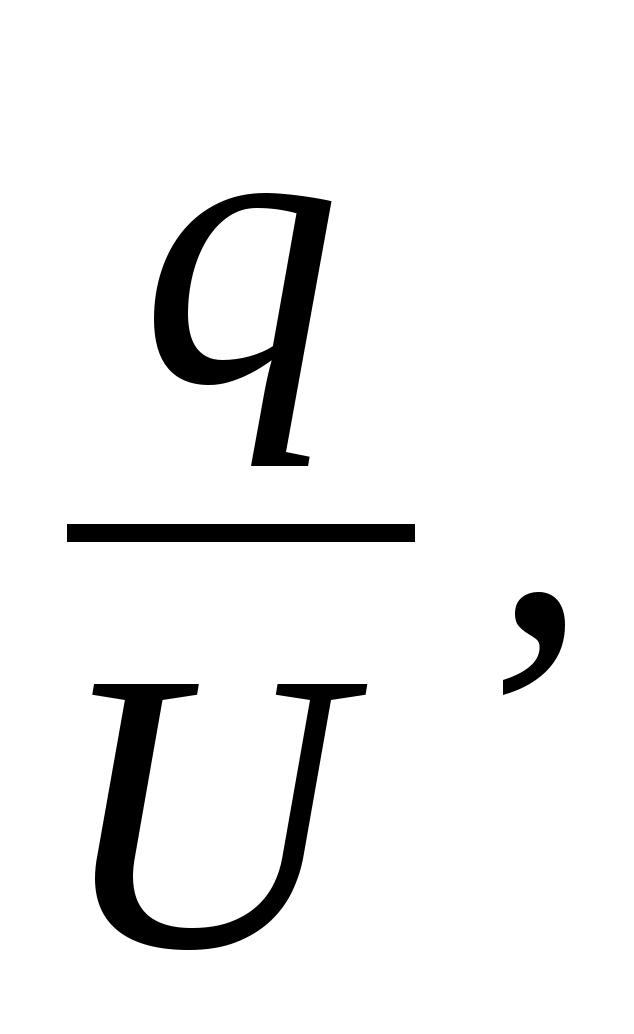 Gdzie q=τl, A
Gdzie q=τl, A
Następnie 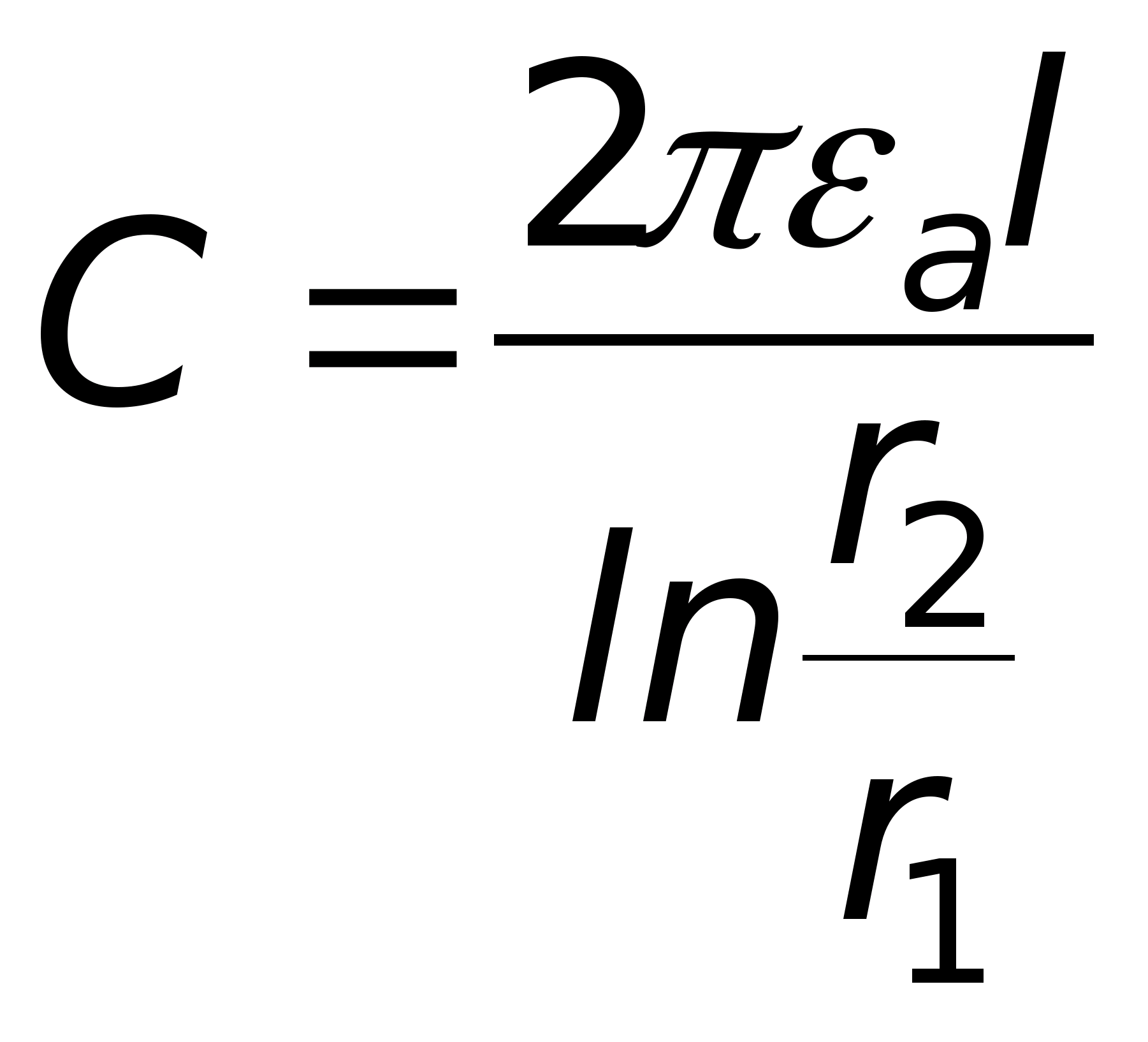 , A
, A 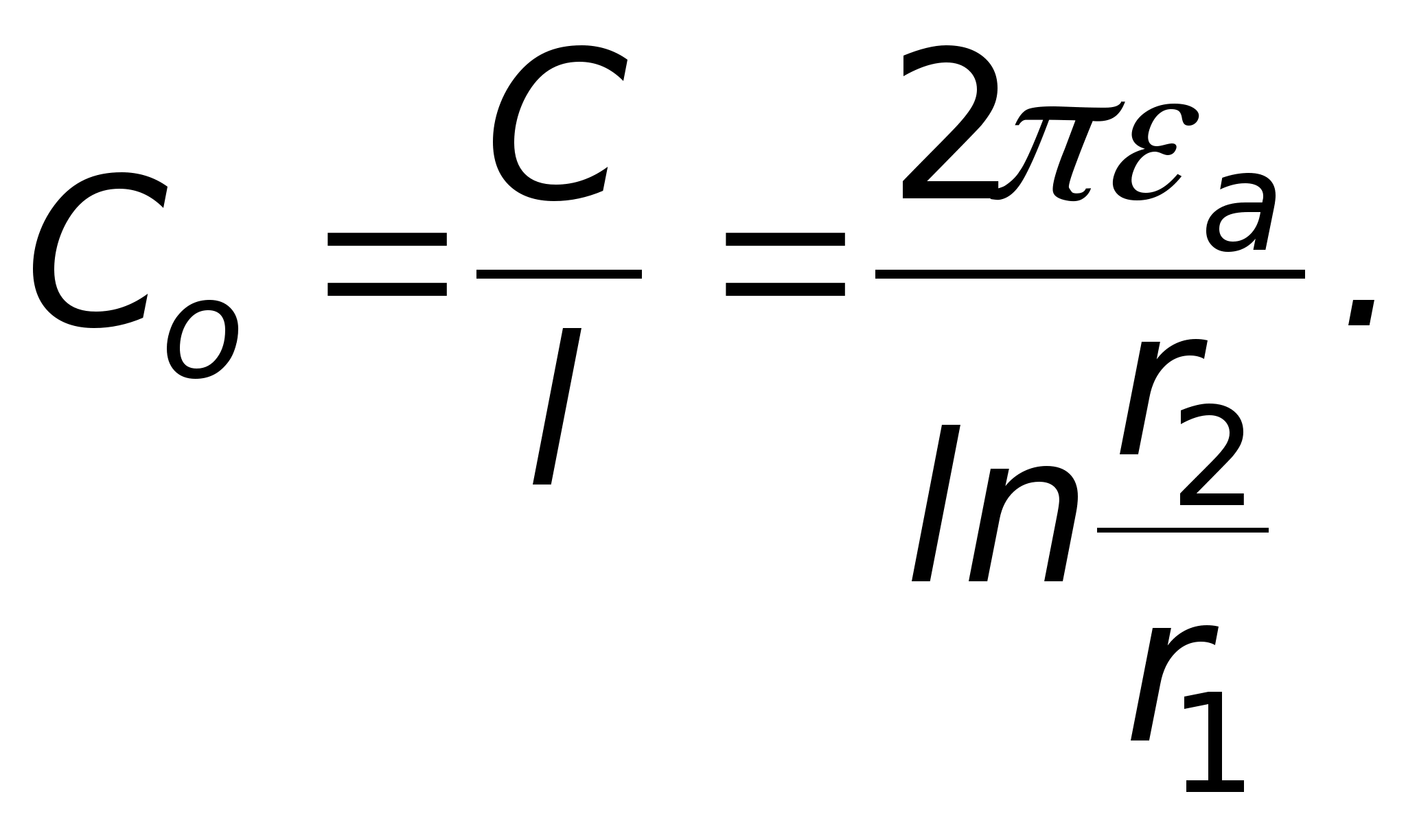
Pole elektrostatyczne i pojemność kondensatorów płaskich jednowarstwowych i dwuwarstwowych
Jednowarstwowy kondensator płaski składa się z dwóch metalowych płytek o przekroju poprzecznym S, położony w pewnej odległości D od siebie (ryc. 11.19). Zdefiniujmy prawo zmiany mi, Co ciekawe, przepływ wektorowy z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy φ
, jeśli zostanie do niego przyłożone napięcie U. Jeśli wymiary płyt (długość, wysokość) są znacznie większe D, wówczas możemy pominąć efekt krawędziowy (zniekształcenie pola na krawędziach płytek) i uznać jego pole elektrostatyczne za jednorodne, tj. dla wszystkich wartości X siła pola jest taka sama. Następnie 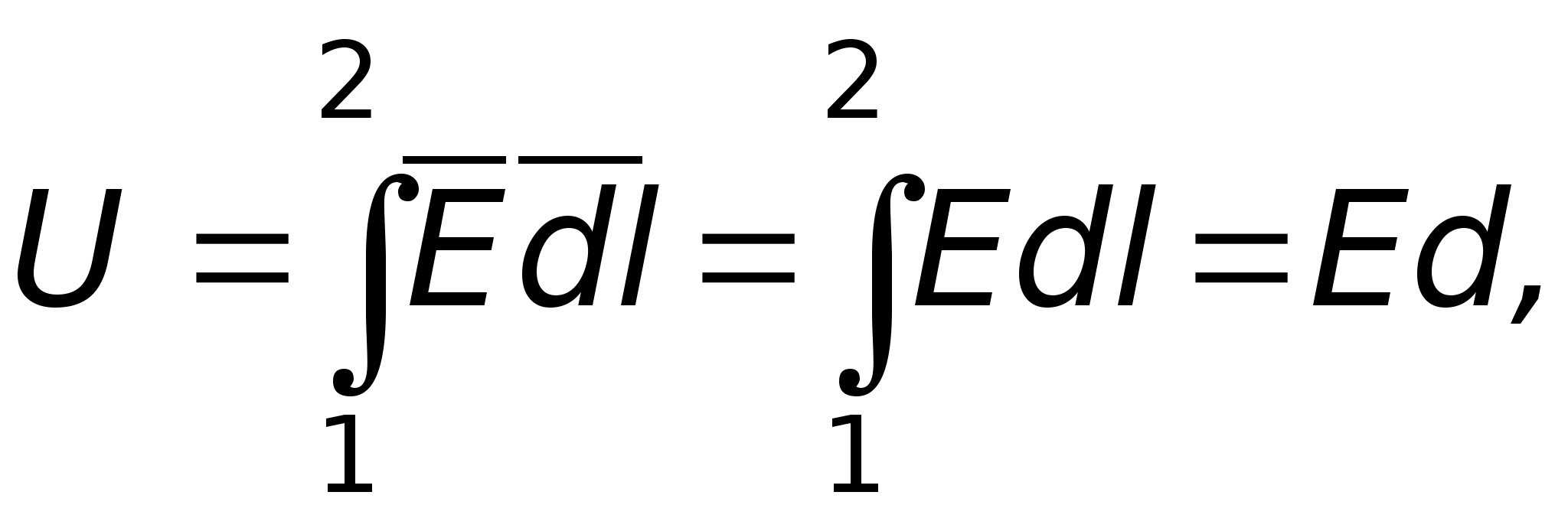 Gdzie
Gdzie
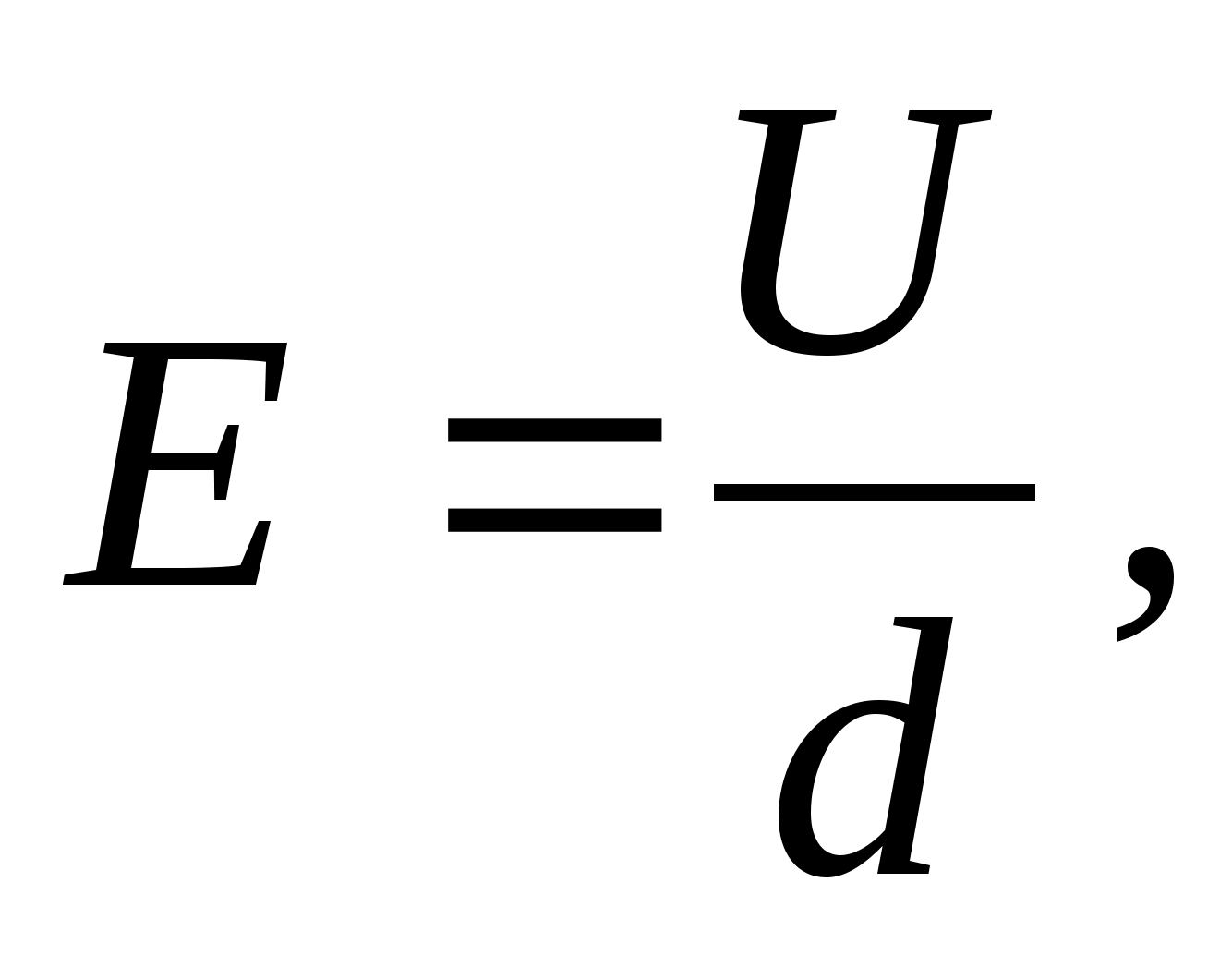 A Co ciekawe, przepływ wektorowy=ε
A E=
A Co ciekawe, przepływ wektorowy=ε
A E= 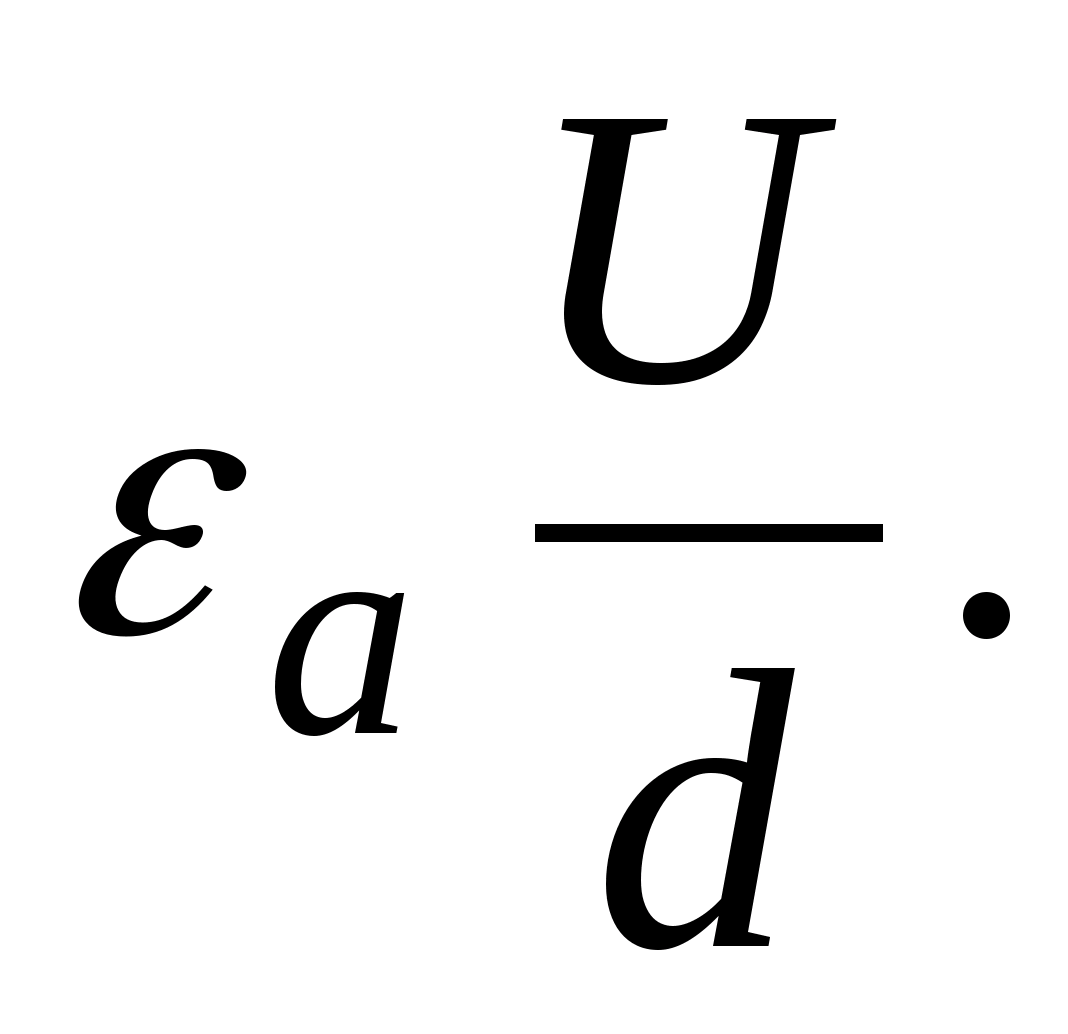 Ponieważ
Ponieważ 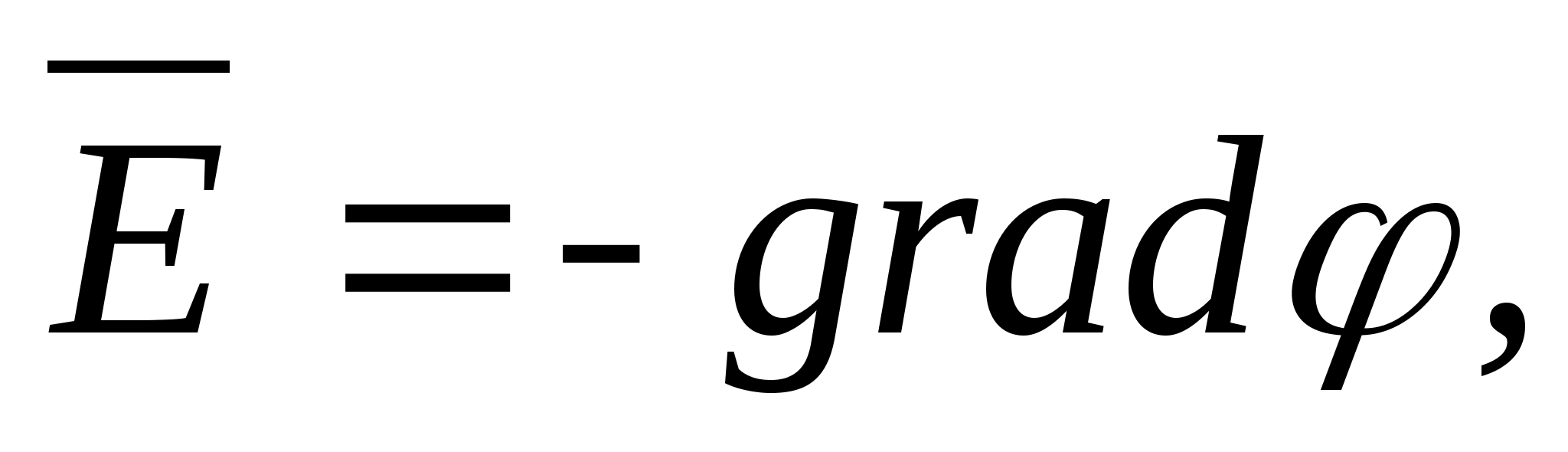 A φ
zależy tylko od X(płaszczyzna Yoz jest ekwipotencjałem), zatem
A φ
zależy tylko od X(płaszczyzna Yoz jest ekwipotencjałem), zatem 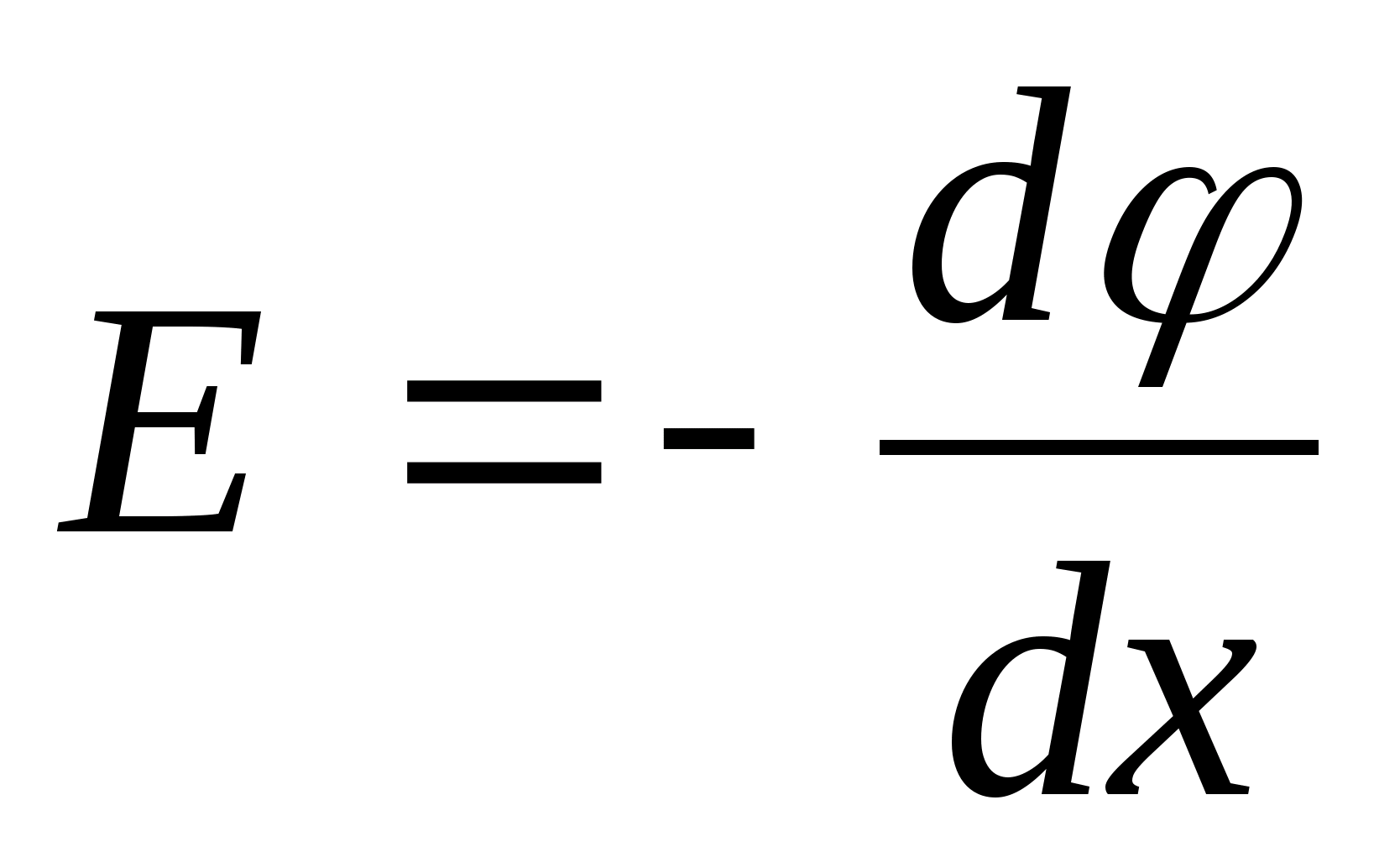 można pominąć ze względu na małą wielkość tych boków. Dla pola potencjalnego, które jest elektrostatyczne,
można pominąć ze względu na małą wielkość tych boków. Dla pola potencjalnego, które jest elektrostatyczne, 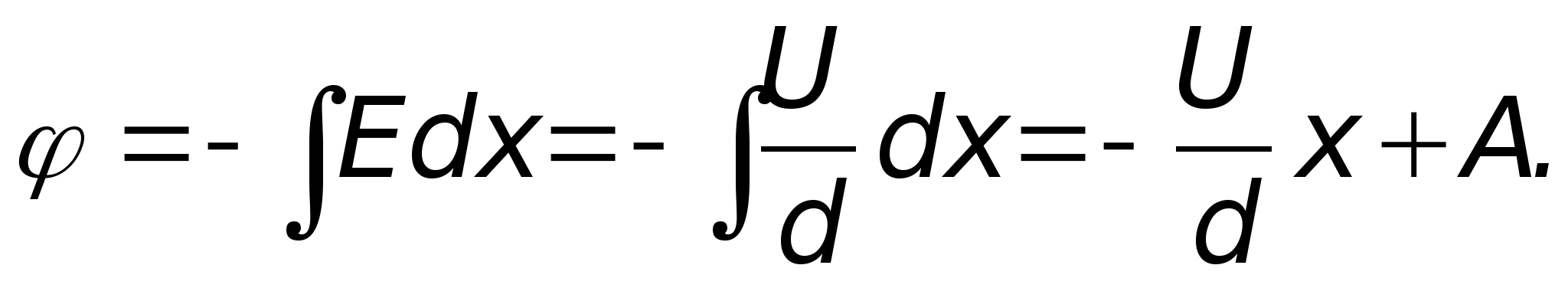 Wyznaczanie stałej całkowania A Załóżmy, że potencjał prawej płytki wynosi zero, a potencjał lewej jest równy U, tj. Na X=0
φ=
U. Następnie A=U, ponieważ wektory
Wyznaczanie stałej całkowania A Załóżmy, że potencjał prawej płytki wynosi zero, a potencjał lewej jest równy U, tj. Na X=0
φ=
U. Następnie A=U, ponieważ wektory 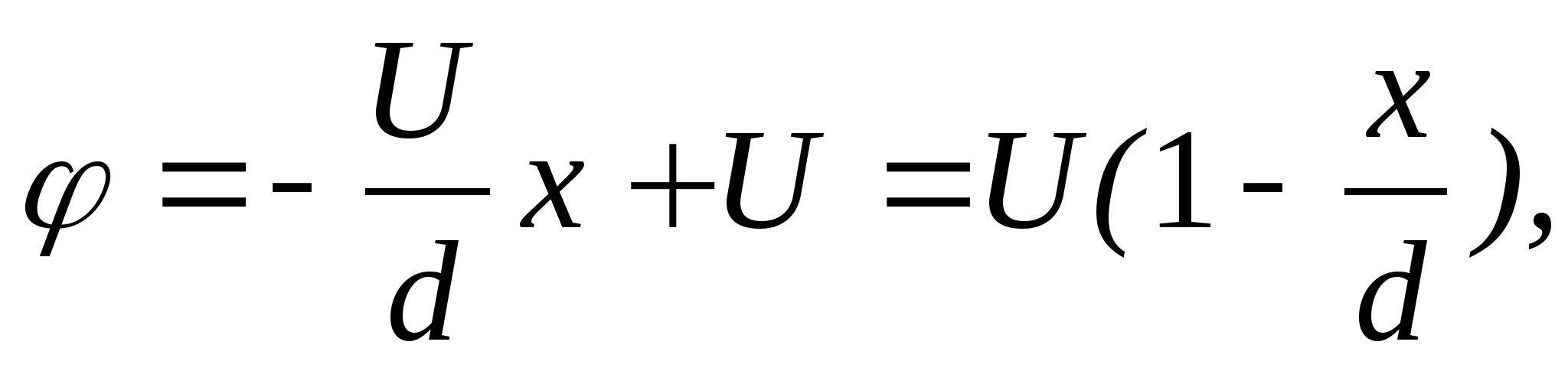 te. φ
zmienia się liniowo w zależności od X.
te. φ
zmienia się liniowo w zależności od X.
Określmy pojemność płaskiego kondensatora Z= gdzie U = wyd. Aby wyznaczyć ładunek np. lewej płytki, korzystamy z twierdzenia Gaussa: 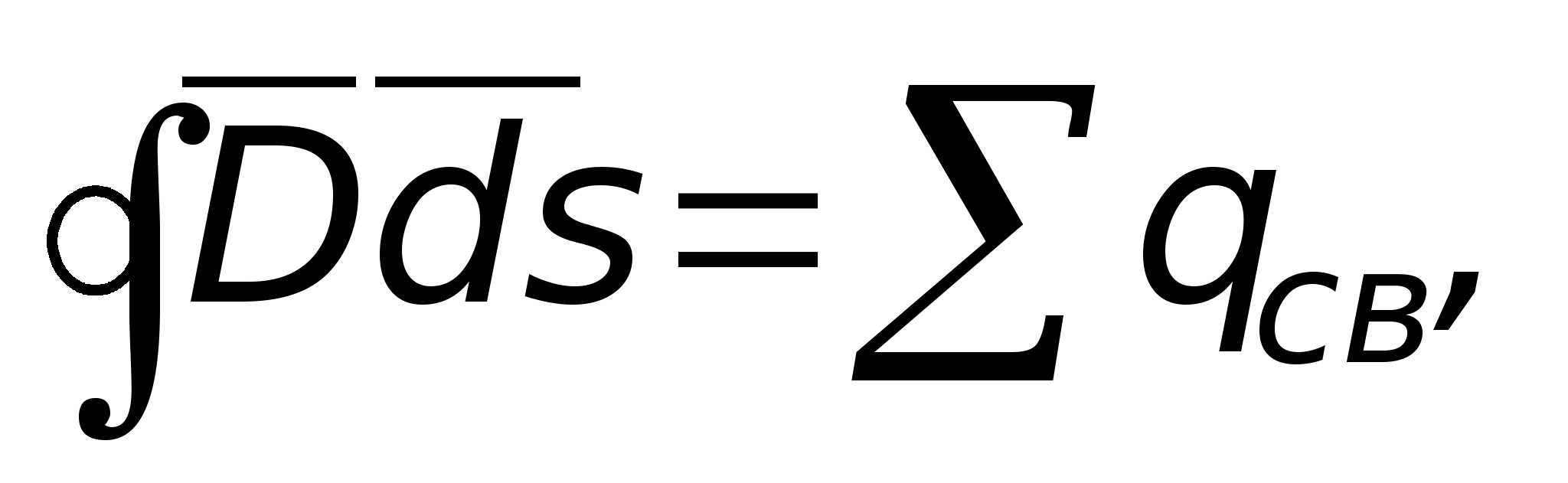 I
I 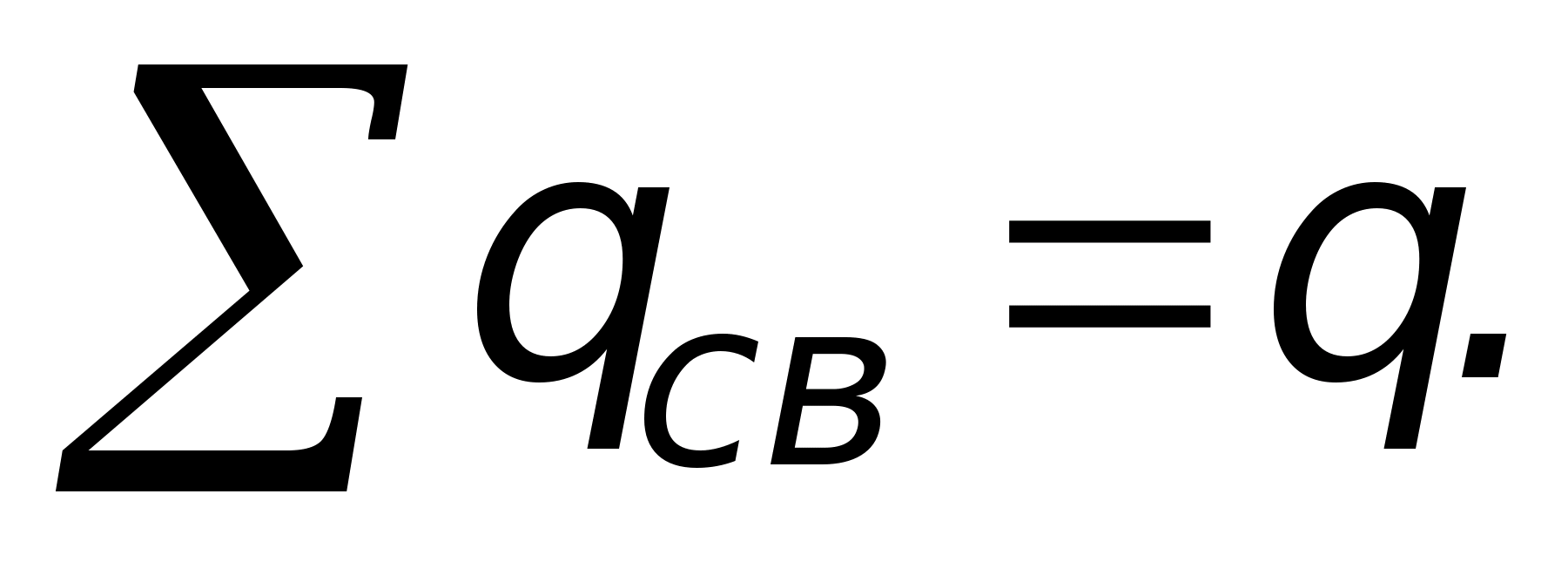 Zdefiniujmy przepływ wektorowy Co ciekawe, przepływ wektorowy przez zamkniętą powierzchnię otaczającą tę płytkę (ryc. 11.19)
Zdefiniujmy przepływ wektorowy Co ciekawe, przepływ wektorowy przez zamkniętą powierzchnię otaczającą tę płytkę (ryc. 11.19) 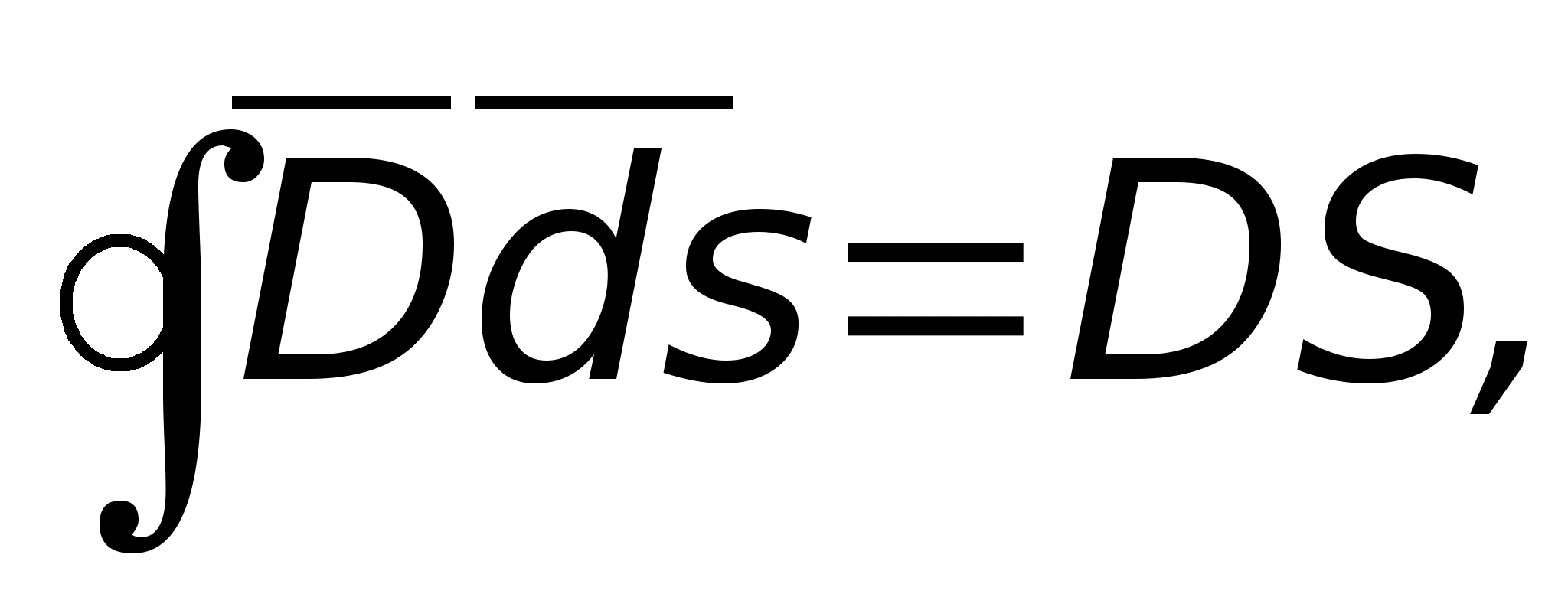 ponieważ wektory Co ciekawe, przepływ wektorowy z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory pokrywają się w kierunku i Co ciekawe, przepływ wektorowy ma tę samą wartość we wszystkich punktach kondensatora. Stąd, q=DS=
ε
A ES I
ponieważ wektory Co ciekawe, przepływ wektorowy z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory pokrywają się w kierunku i Co ciekawe, przepływ wektorowy ma tę samą wartość we wszystkich punktach kondensatora. Stąd, q=DS=
ε
A ES I 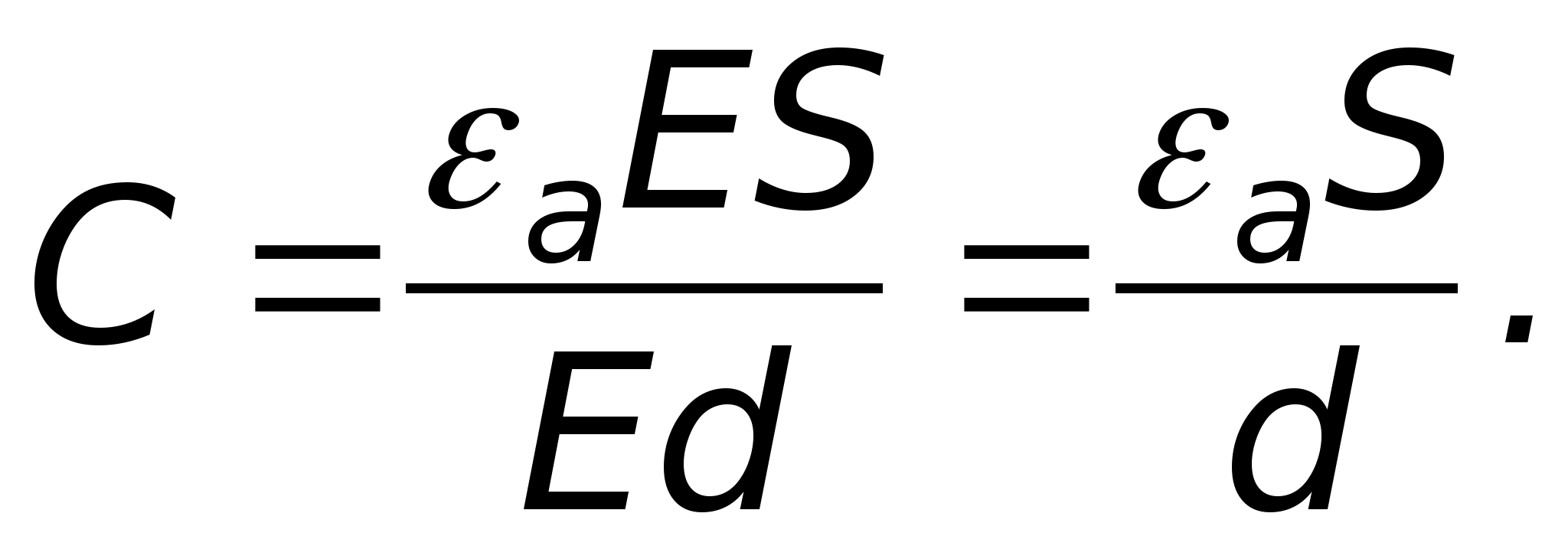
D 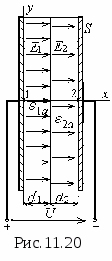 Kondensator dwuwarstwowy (ryc. 11.20) różni się od poprzedniego tym, że izolacja między płytami składa się z dwóch warstw o przepuszczalności ε 1a i ε 2a. Jeśli w dalszym ciągu zaniedbujemy efekt krawędziowy, wówczas pole takiego kondensatora charakteryzuje się tym, że w każdej warstwie jest ono jednolite z mocami mi 1 i mi 2 odpowiednio. Następnie
Kondensator dwuwarstwowy (ryc. 11.20) różni się od poprzedniego tym, że izolacja między płytami składa się z dwóch warstw o przepuszczalności ε 1a i ε 2a. Jeśli w dalszym ciągu zaniedbujemy efekt krawędziowy, wówczas pole takiego kondensatora charakteryzuje się tym, że w każdej warstwie jest ono jednolite z mocami mi 1 i mi 2 odpowiednio. Następnie 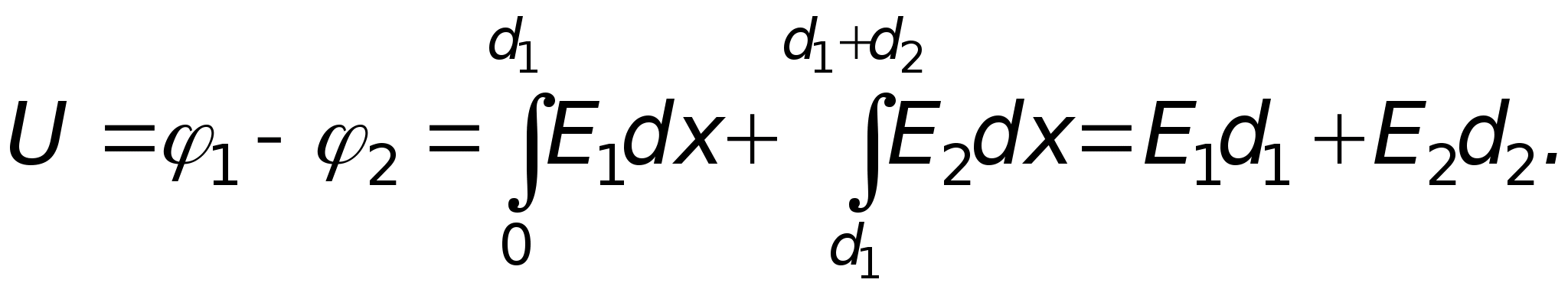 Jednak to równanie nie wystarczy do ustalenia mi 1 i mi 2. Aby utworzyć drugie równanie, używamy warunków brzegowych. Wiadomo, że na styku dwóch różnych dielektryków składowe normalne wektora indukcji elektrostatycznej są równe ( Co ciekawe, przepływ wektorowy 1 stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. 1n 2 stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest.). Jeśli weźmiemy pod uwagę, że w naszym przypadku wektory te są prostopadłe do granicy, to równość ta przybierze postać Co ciekawe, przepływ wektorowy 1 =Co ciekawe, przepływ wektorowy 2 lub ε
1 A mi 1 =
ε
2 A mi 2. To będzie drugie równanie. Rozwiązując te równania razem, otrzymujemy
Jednak to równanie nie wystarczy do ustalenia mi 1 i mi 2. Aby utworzyć drugie równanie, używamy warunków brzegowych. Wiadomo, że na styku dwóch różnych dielektryków składowe normalne wektora indukcji elektrostatycznej są równe ( Co ciekawe, przepływ wektorowy 1 stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. 1n 2 stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest.). Jeśli weźmiemy pod uwagę, że w naszym przypadku wektory te są prostopadłe do granicy, to równość ta przybierze postać Co ciekawe, przepływ wektorowy 1 =Co ciekawe, przepływ wektorowy 2 lub ε
1 A mi 1 =
ε
2 A mi 2. To będzie drugie równanie. Rozwiązując te równania razem, otrzymujemy
Zdefiniujmy prawo potencjalnej zmiany:
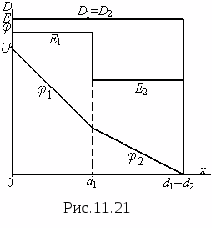
Stała całkowania A 1 wyznaczamy z warunku, że kiedy X=0 φ 1 = U (A 1 =U), A A 2 – od warunku, że kiedy X=D 1 φ 1 =φ 2 (lub φ 2 = 0 o godz X=D 1 +D 2). Z otrzymanych wzorów wynika, że potencjał zmienia się zgodnie z prawem liniowym. Rysunek 11.21 przedstawia wykresy zależności od X indukcje, napięcia i potencjały.
Pojemność takiego kondensatora definiuje się jako równoważną dwóm pojemnościom połączonym szeregowo:
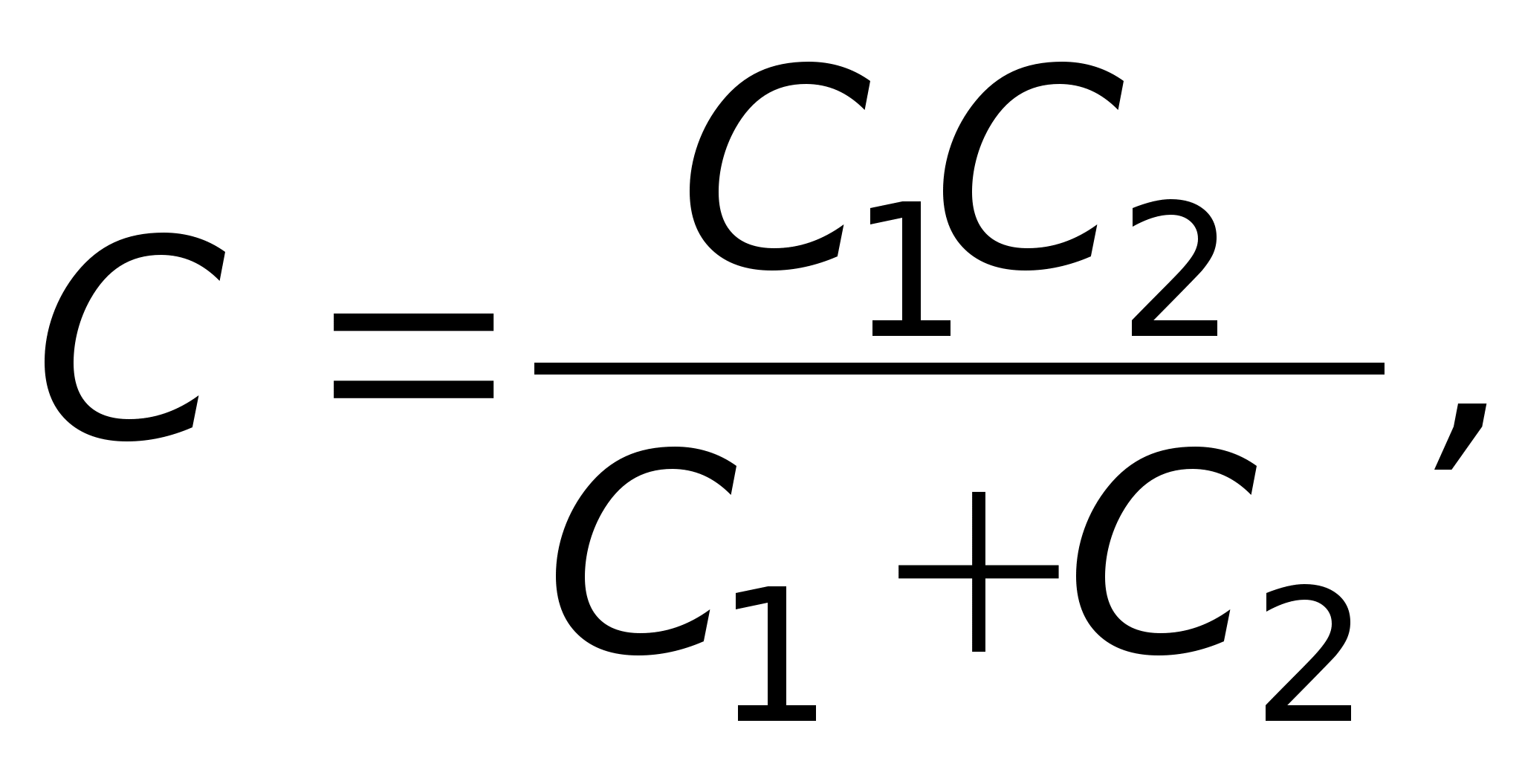 Gdzie
Gdzie 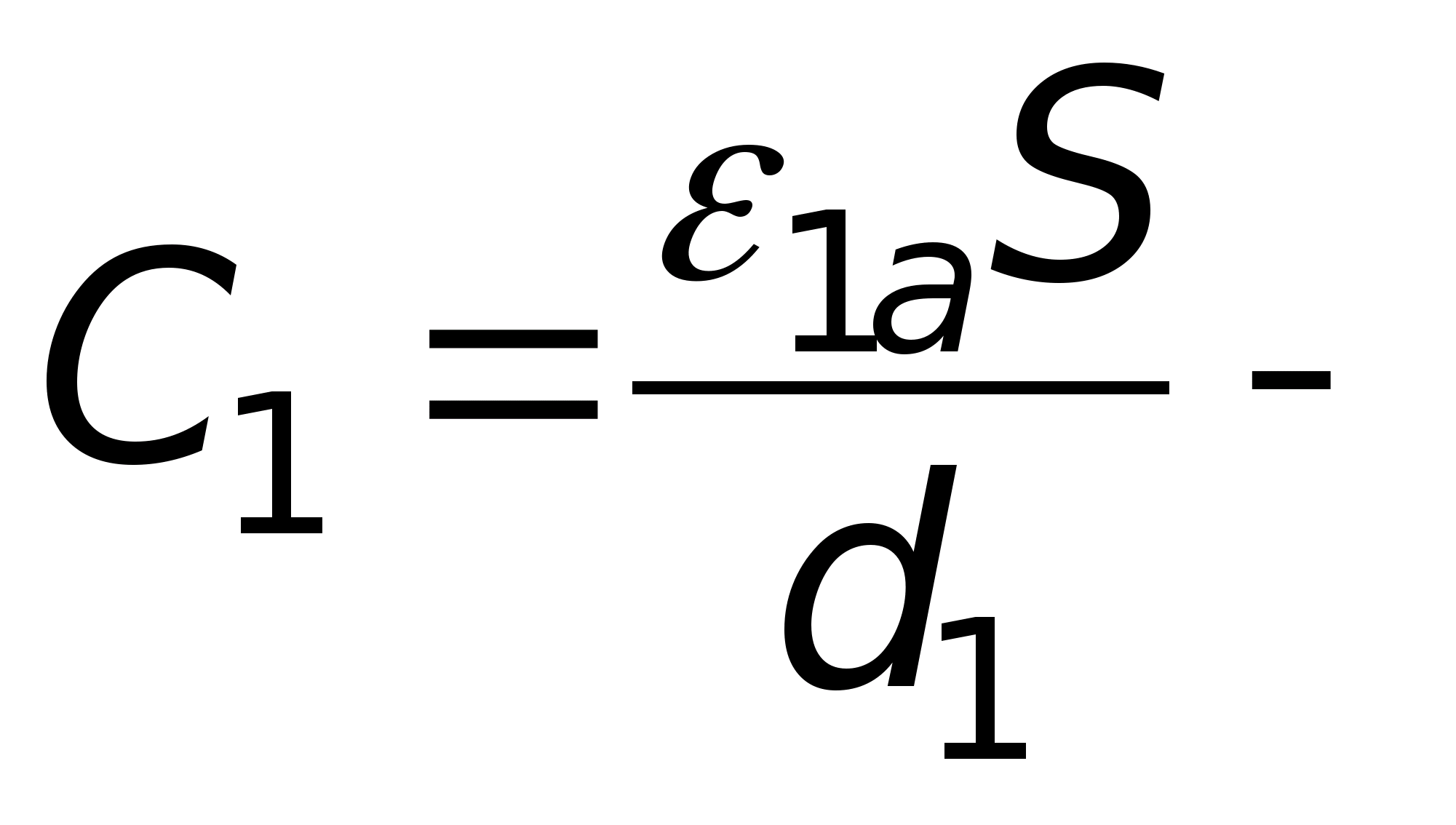 pojemność pierwszej warstwy i
pojemność pierwszej warstwy i 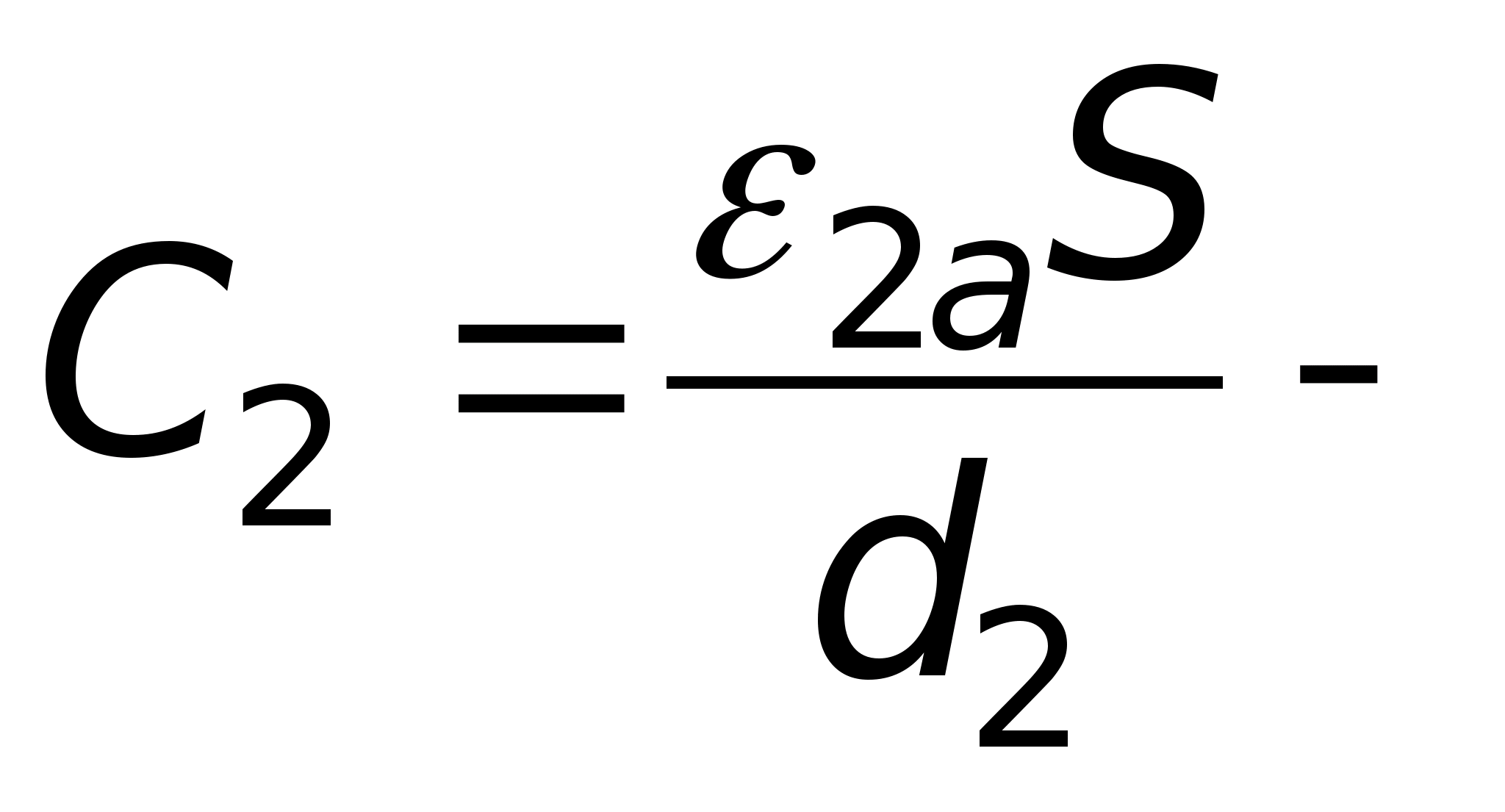 pojemność drugiej warstwy izolacji kondensatora.
pojemność drugiej warstwy izolacji kondensatora.
Metoda odbicia lustrzanego
Metoda ta służy do obliczania pól, w których występuje geometria poprawna forma interfejs pomiędzy różnymi mediami. Jest to sztuczna metoda obliczeniowa, której istota polega na tym, że oprócz podanych ładunków do obliczeń wprowadzane są ładunki dodatkowe lub fikcyjne, których wielkość i położenie dobiera się tak, aby spełnione były warunki brzegowe. Najczęściej ładunki fikcyjne lokalizowane są w punktach stanowiących lustrzane odbicie w stosunku do zadanych, stąd nazwa metody. Do obliczeń wprowadza się ładunki dodatkowe lub fikcyjne, aby uwzględnić wpływ ładunków swobodnych lub związanych, powstałych w wyniku indukcji elektrostatycznej.
Pole naładowanej osi znajdującej się w pobliżu powierzchni przewodzącej
P 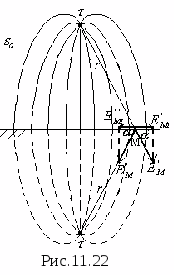 mieć naładowaną oś z ładunkiem
umieszczone równolegle do powierzchni ośrodka przewodzącego (ryc. 11.22). Tym medium przewodzącym może być metalowa płyta lub ściana domu, ale najczęściej jest to ziemia. W wyniku indukcji elektrostatycznej na powierzchni ciała przewodzącego indukują się ładunki, których obecność powoduje zniekształcenie pola w porównaniu z polem pojedynczej osi. Rozkład indukowanych ładunków na powierzchni ośrodka przewodzącego jest bardzo złożony i nieznany. Mimo to zadaniem obliczenia pola w górnej półprzestrzeni wypełnionej dielektrykiem o przepuszczalności
A(w dolnej półprzestrzeni nie ma pola, ponieważ znajduje się tam ośrodek przewodzący) można rozwiązać w prosty sposób metodą odbicia lustrzanego. Umieśćmy w punkcie będącym lustrzanym odbiciem danej osi względem powierzchni przewodzącej fikcyjną oś z ładunkiem tej samej wielkości, ale o przeciwnym znaku, tj. -
(pamiętaj, że nie zawsze tak będzie; fikcyjne obciążenie może mieć inne wartości i znaki). Upewnijmy się, że napięcie mi z dwóch naładowanych osi (
I -
) w żadnym punkcie interfejsu nie posiada składowej stycznej. A Rzeczywiście, ponieważ składowe styczne obu ładunków mają przeciwne kierunki i sumują się do zera. W rezultacie spełnione są warunki brzegowe pomiędzy dielektrykiem a przewodnikiem, co świadczy o słuszności doboru wielkości i umiejscowienia fikcyjnego ładunku. Dlatego natężenie i potencjał pola w dowolnym punkcie dielektryka można wyznaczyć za pomocą znanych wzorów na pole dwóch naładowanych osi: gdzie B– odległość do dodatnio naładowanej osi,
– odległość do osi naładowanej ujemnie. Jeśli rzeczywista oś miała ładunek -
, to problem zostałby rozwiązany w podobny sposób, tylko fikcyjna oś miałaby ładunek +
mieć naładowaną oś z ładunkiem
umieszczone równolegle do powierzchni ośrodka przewodzącego (ryc. 11.22). Tym medium przewodzącym może być metalowa płyta lub ściana domu, ale najczęściej jest to ziemia. W wyniku indukcji elektrostatycznej na powierzchni ciała przewodzącego indukują się ładunki, których obecność powoduje zniekształcenie pola w porównaniu z polem pojedynczej osi. Rozkład indukowanych ładunków na powierzchni ośrodka przewodzącego jest bardzo złożony i nieznany. Mimo to zadaniem obliczenia pola w górnej półprzestrzeni wypełnionej dielektrykiem o przepuszczalności
A(w dolnej półprzestrzeni nie ma pola, ponieważ znajduje się tam ośrodek przewodzący) można rozwiązać w prosty sposób metodą odbicia lustrzanego. Umieśćmy w punkcie będącym lustrzanym odbiciem danej osi względem powierzchni przewodzącej fikcyjną oś z ładunkiem tej samej wielkości, ale o przeciwnym znaku, tj. -
(pamiętaj, że nie zawsze tak będzie; fikcyjne obciążenie może mieć inne wartości i znaki). Upewnijmy się, że napięcie mi z dwóch naładowanych osi (
I -
) w żadnym punkcie interfejsu nie posiada składowej stycznej. A Rzeczywiście, ponieważ składowe styczne obu ładunków mają przeciwne kierunki i sumują się do zera. W rezultacie spełnione są warunki brzegowe pomiędzy dielektrykiem a przewodnikiem, co świadczy o słuszności doboru wielkości i umiejscowienia fikcyjnego ładunku. Dlatego natężenie i potencjał pola w dowolnym punkcie dielektryka można wyznaczyć za pomocą znanych wzorów na pole dwóch naładowanych osi: gdzie B– odległość do dodatnio naładowanej osi,
– odległość do osi naładowanej ujemnie. Jeśli rzeczywista oś miała ładunek -
, to problem zostałby rozwiązany w podobny sposób, tylko fikcyjna oś miałaby ładunek +
. W podobny sposób rozwiązuje się problem pola ładunku punktowego znajdującego się w pobliżu ośrodka przewodzącego.
W 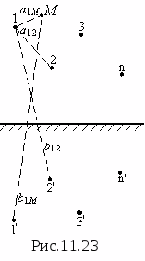 Pole elektrostatyczne układu przewodników znajdujących się w pobliżu powierzchni przewodzącej (pojemności cząstkowe) stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. Jako system przewodów umieszczonych w pobliżu powierzchni przewodzącej należy rozważyć wieloprzewodową linię elektroenergetyczną (PTL), składającą się z:
Pole elektrostatyczne układu przewodników znajdujących się w pobliżu powierzchni przewodzącej (pojemności cząstkowe) stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. Jako system przewodów umieszczonych w pobliżu powierzchni przewodzącej należy rozważyć wieloprzewodową linię elektroenergetyczną (PTL), składającą się z:
bardzo długie druty rozciągnięte równolegle do powierzchni ziemi (ryc. 11.23). Niech będą znane ładunki każdego drutu R k (uważymy je za dodatnie), ich promienie k, wysokość zawieszenia H A k, względne położenie i właściwości środowiska ( stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest.), w którym się znajdują. W wyniku indukcji elektrostatycznej na powierzchni ziemi pojawią się swobodne ładunki, które będą miały wpływ na powstałe pole elektrostatyczne. Aby uwzględnić ten wpływ, zastosujemy metodę odbicia lustrzanego, dla której wprowadzimy do obliczeń M fikcyjne przewody umieszczone w punktach lustrzanego odbicia w stosunku do zadanych. Weźmy dowolny punkt dielektryka M = M 1 ` + M 2 + M 3 +…+ M i określić jego potencjał metodą superpozycji: M n., gdzie M 1 – składnik potencjalny utworzony przez pierwszy przewód i jego lustrzane odbicie,
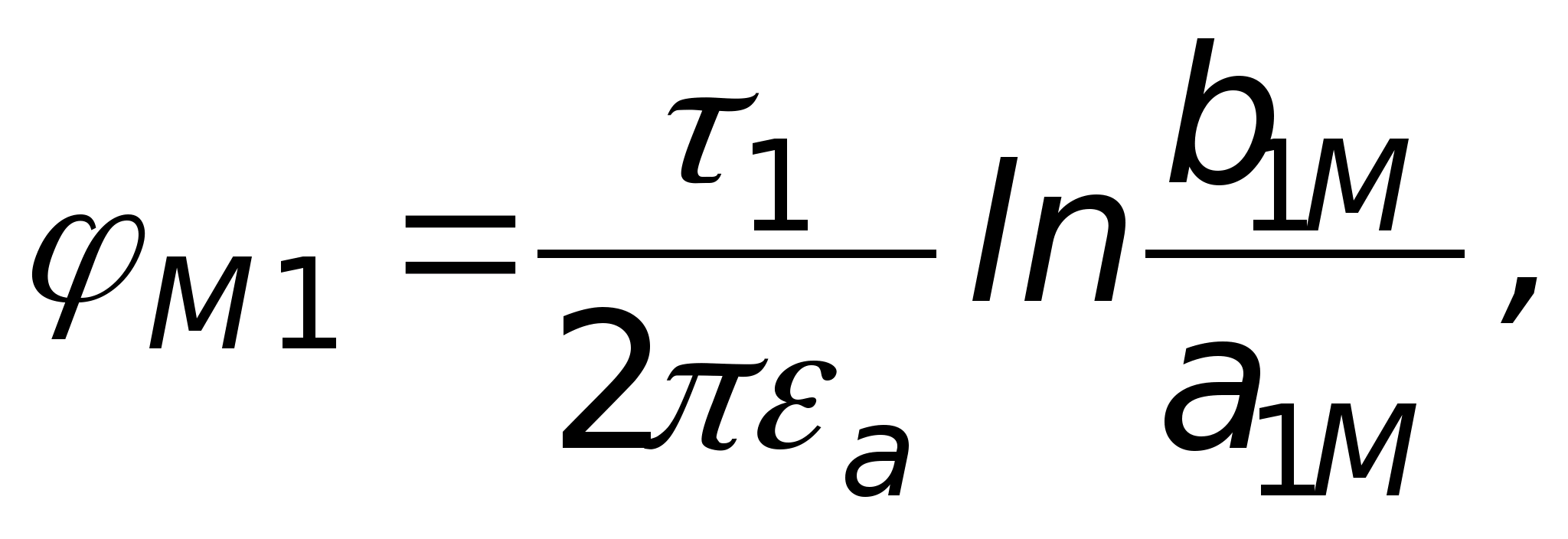 Gdzie A 1 M 2 - element utworzony przez drugi przewód i jego lustrzane odbicie itp. Zakładamy, że wysokości zawieszenia drutów są znacznie większe niż ich promienie, a następnie możemy założyć, że osie elektryczne i geometryczne drutów pokrywają się. Mając to na uwadze, możemy napisać: M- odległość od punktu B 1 do osi pierwszego drutu; M M– odległość od punktu
Gdzie A 1 M 2 - element utworzony przez drugi przewód i jego lustrzane odbicie itp. Zakładamy, że wysokości zawieszenia drutów są znacznie większe niż ich promienie, a następnie możemy założyć, że osie elektryczne i geometryczne drutów pokrywają się. Mając to na uwadze, możemy napisać: M- odległość od punktu B 1 do osi pierwszego drutu; M M– odległość od punktu 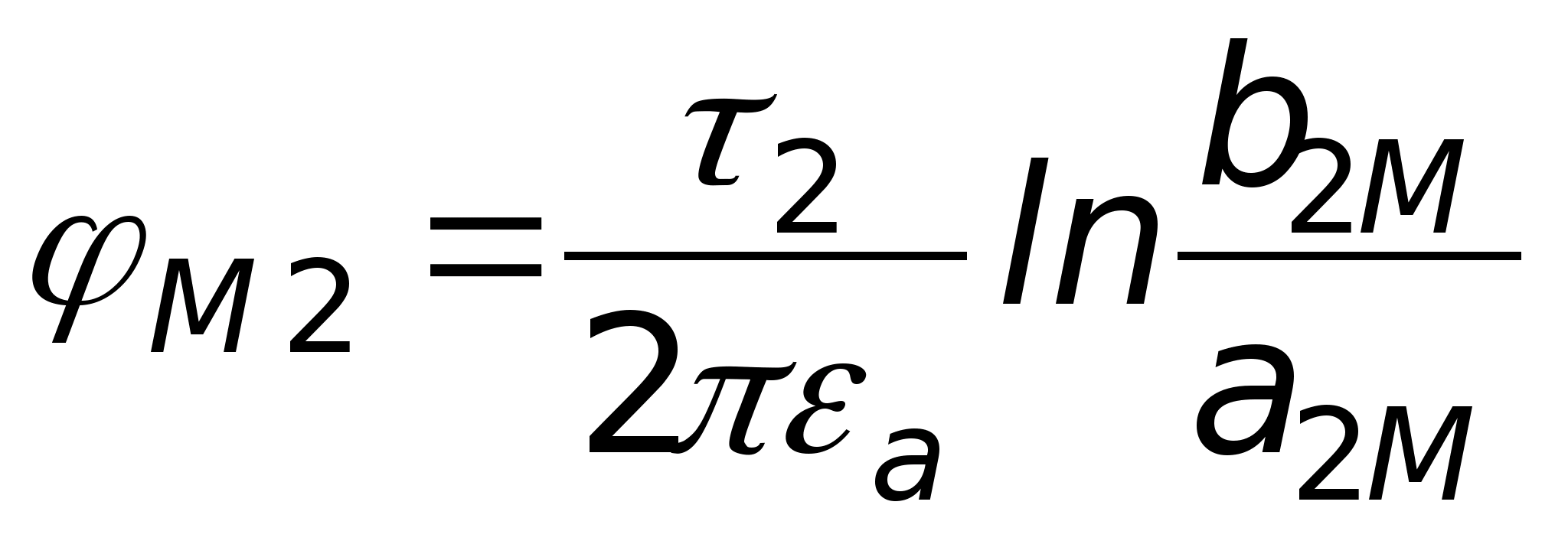 do lustrzanego odbicia pierwszego drutu;
do lustrzanego odbicia pierwszego drutu;
itp. Następnie M Jeśli chodzi o A 1 M =R 1 , B 1 do osi pierwszego drutu; =2k, wysokość zawieszenia 1 , A 2 M =A umieszczony na powierzchni pierwszego drutu, wówczas jego potencjał można wyznaczyć za pomocą tego wzoru, biorąc pod uwagę to B 2 do osi pierwszego drutu; =12 – odległość pomiędzy pierwszym i drugim przewodnikiem, 12 - odległość od pierwszego przewodnika do lustrzanego odbicia drugiego itd., a następnie otrzymujemy
Podobnie możesz wyznaczyć potencjały wszystkich przewodów linii energetycznej i jeśli to zrobisz, otrzymasz pierwszą grupę wzorów Maxwella:
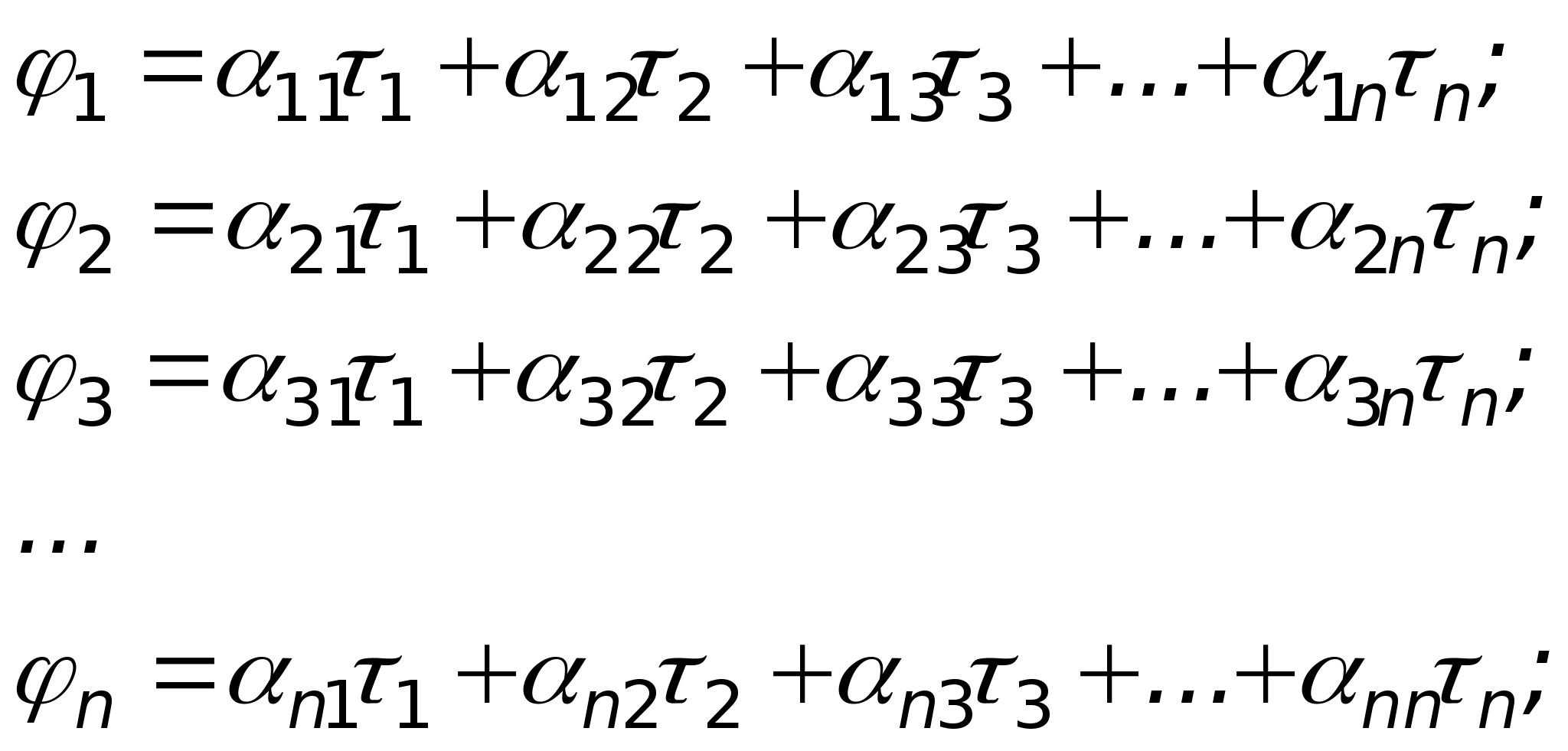
W tych równaniach współczynniki kk z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy Do =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw zależą jedynie od wymiarów geometrycznych ciał, ich wzajemnego położenia oraz właściwości środowiska, w którym się znajdują. Nazywa się je potencjalnymi współczynnikami i mierzy się je m/k i wszystkie są dodatnie (pod znakiem logarytmu znajduje się ułamek, którego licznik jest zawsze większy od mianownika). Można im dać taką interpretację. Niech ładunki wszystkich drutów z wyjątkiem pierwszego będą zerowe i 1 = 1. Wtedy pierwsza grupa wzorów Maxwella przyjmuje postać: 1 = 11 ; 2 = 21 ; 3 = 31 ; … n= nr 1. Stąd, 11 jest równe potencjałowi pierwszego drutu, jeśli ładunek na nim wynosi 1, a pozostałe przewody nie mają ładunku, 21 jest równy potencjałowi drugiego drutu w określonych warunkach itp.
Pierwsza grupa wzorów Maxwella wyznacza potencjały drutów na podstawie ich ładunków. Jednak w praktyce często pojawia się odwrotny problem wyznaczania ładunków drutów na podstawie ich potencjałów. Można tego dokonać, rozwiązując pierwszą grupę wzorów Maxwella dla ładunków, wyznaczając potencjały i współczynniki drutu słynny. Otrzymujemy wówczas drugą grupę wzorów Maxwella:
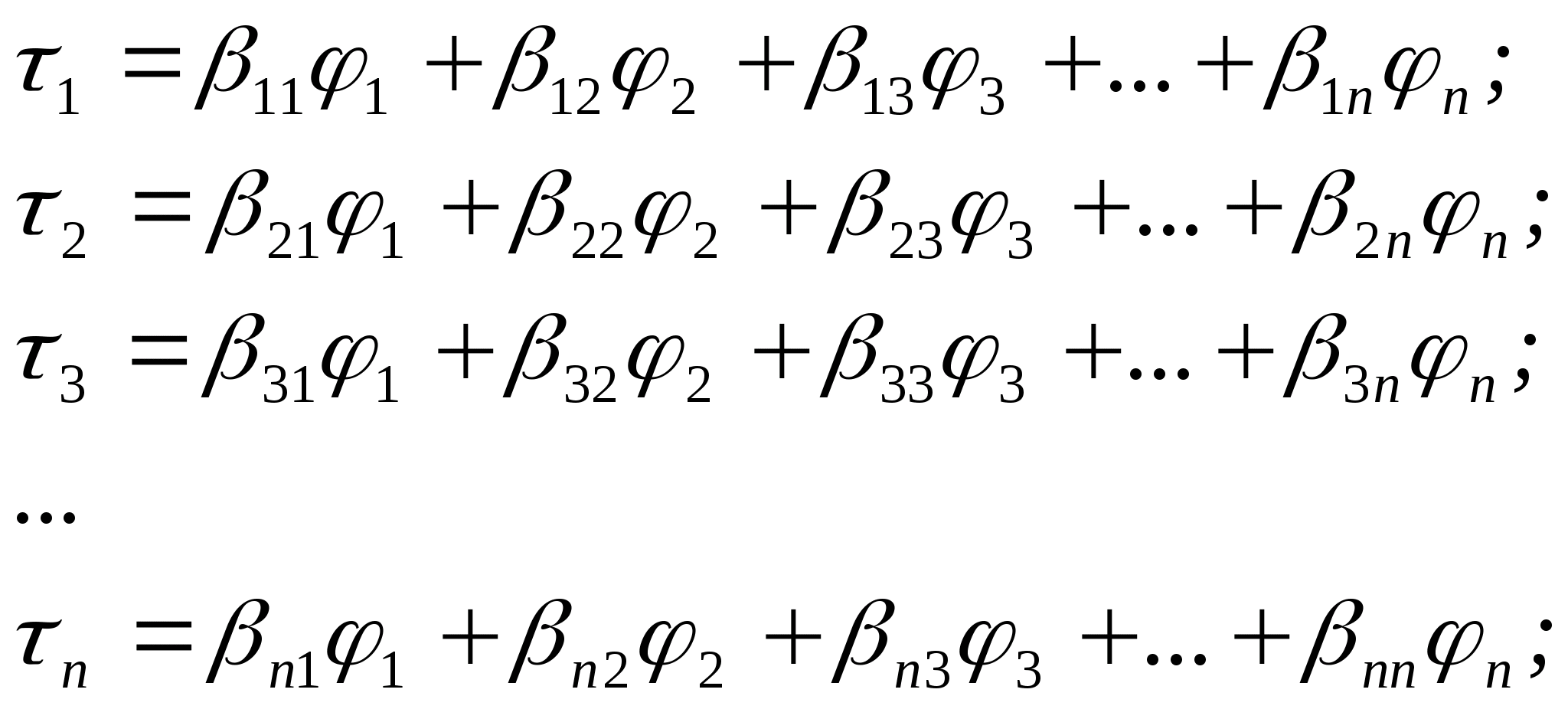
H 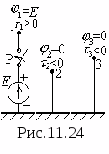 Tutaj
Tutaj ![]() gdzie jest głównym wyznacznikiem pierwszej grupy wzorów Maxwella, składającej się z potencjalnych współczynników
, oraz do m jest dodatkiem algebraicznym uzyskanym z przez usunięcie Do-ta linia, =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw kolumnie i pomnożyć pozostały wyznacznik przez
gdzie jest głównym wyznacznikiem pierwszej grupy wzorów Maxwella, składającej się z potencjalnych współczynników
, oraz do m jest dodatkiem algebraicznym uzyskanym z przez usunięcie Do-ta linia, =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw kolumnie i pomnożyć pozostały wyznacznik przez  Wymiar współczynników pojemnościowych jest odwrotnością wymiaru współczynników potencjalnych, tj. P/m, od km o rząd wielkości mniej niż główny wyznacznik . Współczynniki pojemności mają różne znaki, a mianowicie
kk>0 i
Do M( Do
M) 1 =mi, łącząc go z ziemią, na przykład poprzez źródło stałego pola elektromagnetycznego (ryc. 11.24). Następnie na pierwszym przewodzie zgromadzi się pewien ładunek dodatni
1, i dokładnie ten sam ładunek ujemny rozprzestrzeni się po całej Ziemi i ciałach z nią połączonych. Części ładunku ujemnego spadną na drugi i trzeci przewodnik. Jeśli przepiszemy drugą grupę wzorów Maxwella dla tego doświadczenia, otrzymamy:
1 =
11
1 ;
2 =
21
1 ;
3 =
3 1
1 ,
Wymiar współczynników pojemnościowych jest odwrotnością wymiaru współczynników potencjalnych, tj. P/m, od km o rząd wielkości mniej niż główny wyznacznik . Współczynniki pojemności mają różne znaki, a mianowicie
kk>0 i
Do M( Do
M) 1 =mi, łącząc go z ziemią, na przykład poprzez źródło stałego pola elektromagnetycznego (ryc. 11.24). Następnie na pierwszym przewodzie zgromadzi się pewien ładunek dodatni
1, i dokładnie ten sam ładunek ujemny rozprzestrzeni się po całej Ziemi i ciałach z nią połączonych. Części ładunku ujemnego spadną na drugi i trzeci przewodnik. Jeśli przepiszemy drugą grupę wzorów Maxwella dla tego doświadczenia, otrzymamy:
1 =
11
1 ;
2 =
21
1 ;
3 =
3 1
1 ,
O 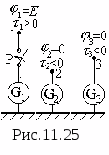 gdzie mamy: Współczynniki pojemności można wyznaczyć eksperymentalnie. Jeżeli po naładowaniu układu włączymy galwanometry G 1 -G 3 (Rys. 11.25) i zamkniemy kluczyk, układ rozładuje się i podczas procesu rozładowywania galwanometry będą mierzyć ładunki
1 -
odpowiednio 3. Następnie, zgodnie z ostatnimi formułami, wiedza
1, można ustalić
11 -
31. Należy to odnotować
Do =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw =
mk, od Do =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw = mk ze względu na symetrię względem głównej przekątnej.
gdzie mamy: Współczynniki pojemności można wyznaczyć eksperymentalnie. Jeżeli po naładowaniu układu włączymy galwanometry G 1 -G 3 (Rys. 11.25) i zamkniemy kluczyk, układ rozładuje się i podczas procesu rozładowywania galwanometry będą mierzyć ładunki
1 -
odpowiednio 3. Następnie, zgodnie z ostatnimi formułami, wiedza
1, można ustalić
11 -
31. Należy to odnotować
Do =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw =
mk, od Do =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw = mk ze względu na symetrię względem głównej przekątnej.
Druga grupa wzorów Maxwella jest niewygodna, ponieważ uwzględnia potencjały przewodów, a nie napięcia między nimi. Dlatego często ten układ jest przepisywany tak, że po prawej stronie znajdują się napięcia pomiędzy danym przewodnikiem a wszystkimi pozostałymi, łącznie z ziemią.
Dowolny wiersz drugiej grupy formuł Maxwella można zapisać w formie zwartej
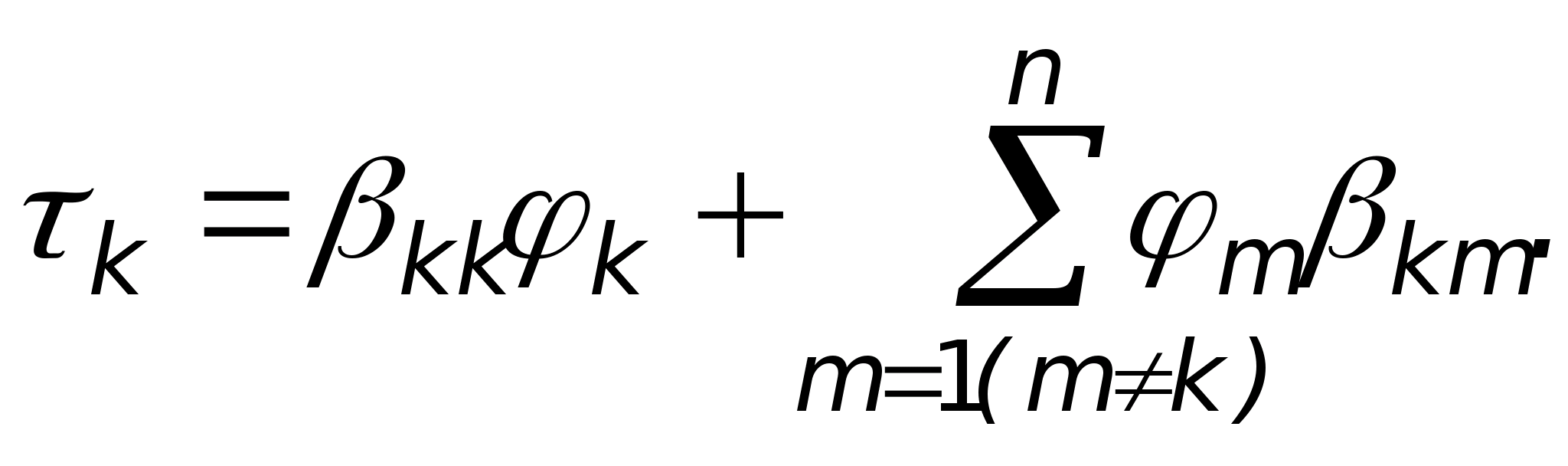 Przekształćmy wyrażenie
Przekształćmy wyrażenie  Gdzie
Gdzie 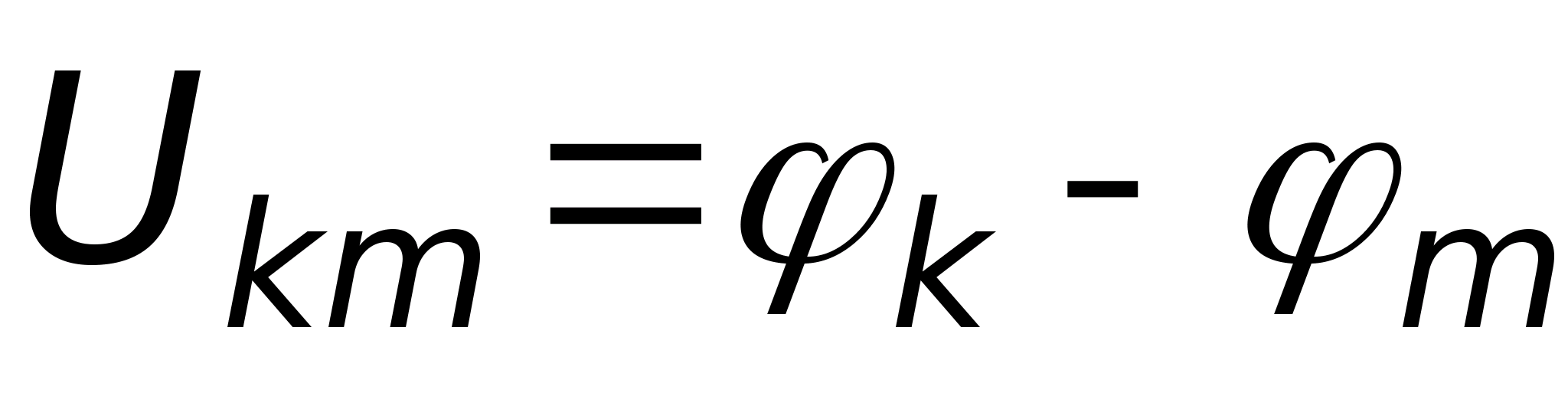 - napięcie pomiędzy Do-m i =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw-m przewody. Następnie, po wyznaczeniu
- napięcie pomiędzy Do-m i =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw-m przewody. Następnie, po wyznaczeniu 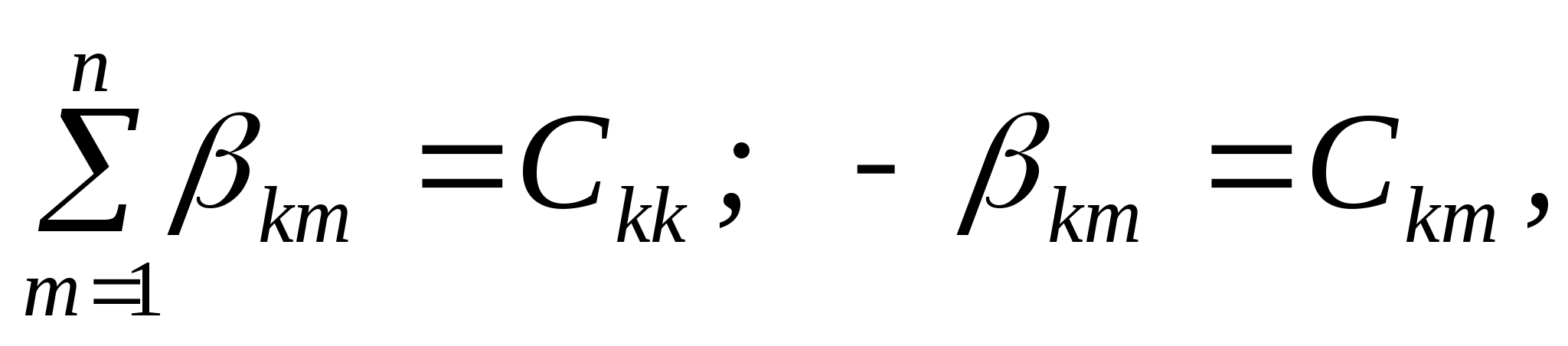 dostajemy
dostajemy 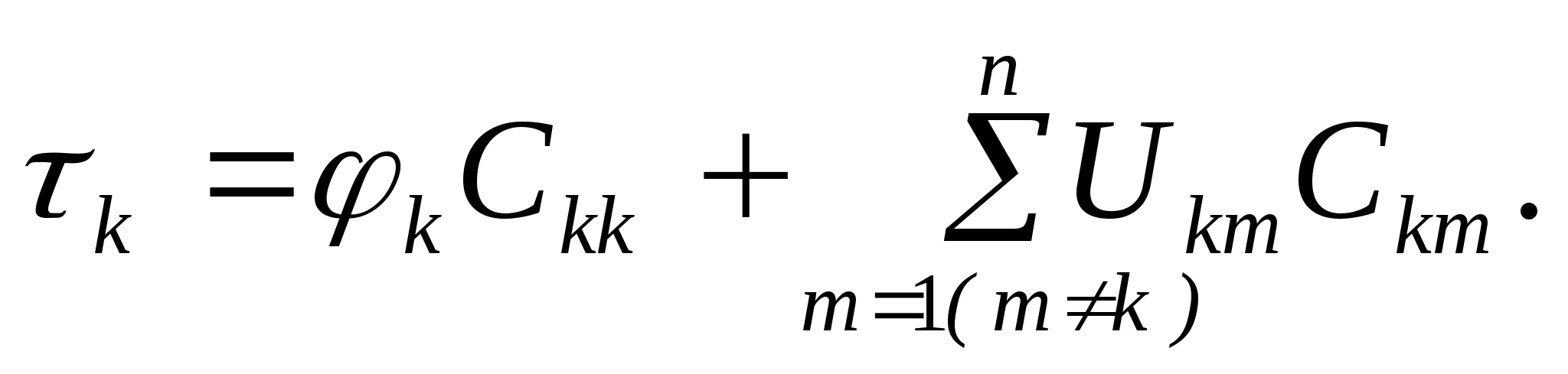 Podanie indeksu k wartości od 1 do stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest., rozpiszmy układ równań, który nazywamy trzecią grupą wzorów Maxwella:
Podanie indeksu k wartości od 1 do stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest., rozpiszmy układ równań, który nazywamy trzecią grupą wzorów Maxwella:
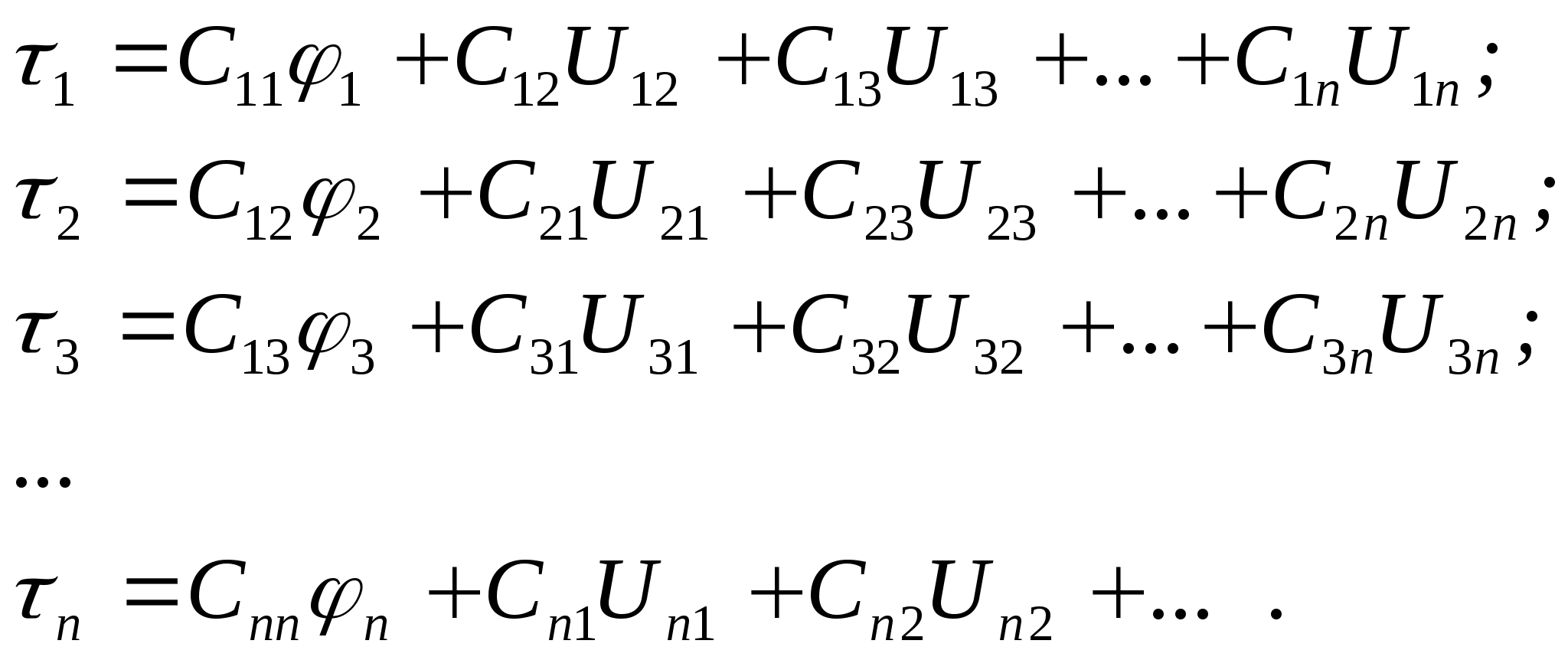
W 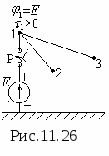 współczynniki wchodzące do tych równań Z nazywane są zdolnościami częściowymi i nazywane są swoją własną zdolnością częściową k dyrygent. We wskazanej sumie tylko jeden wyraz jest dodatni (
kk), niemniej jednak Z kk zawsze pozytywne. Można to sprawdzić wykonując następujący eksperyment: łączymy (cienkimi drutami) wszystkie przewody linii energetycznej z pierwszym i ładujemy ten układ podłączając go do ziemi poprzez źródło stałego pola elektromagnetycznego (rys. 11.26). Następnie na pierwszym przewodzie zgromadzi się pewien ładunek dodatni
1 i jego potencjał
1 =mi>0. Pierwsze równanie trzeciej grupy wzorów Maxwella dla tego doświadczenia ma postać ( U 12 =0,
U 13 =0)
1 =C 11
1, skąd mamy
współczynniki wchodzące do tych równań Z nazywane są zdolnościami częściowymi i nazywane są swoją własną zdolnością częściową k dyrygent. We wskazanej sumie tylko jeden wyraz jest dodatni (
kk), niemniej jednak Z kk zawsze pozytywne. Można to sprawdzić wykonując następujący eksperyment: łączymy (cienkimi drutami) wszystkie przewody linii energetycznej z pierwszym i ładujemy ten układ podłączając go do ziemi poprzez źródło stałego pola elektromagnetycznego (rys. 11.26). Następnie na pierwszym przewodzie zgromadzi się pewien ładunek dodatni
1 i jego potencjał
1 =mi>0. Pierwsze równanie trzeciej grupy wzorów Maxwella dla tego doświadczenia ma postać ( U 12 =0,
U 13 =0)
1 =C 11
1, skąd mamy 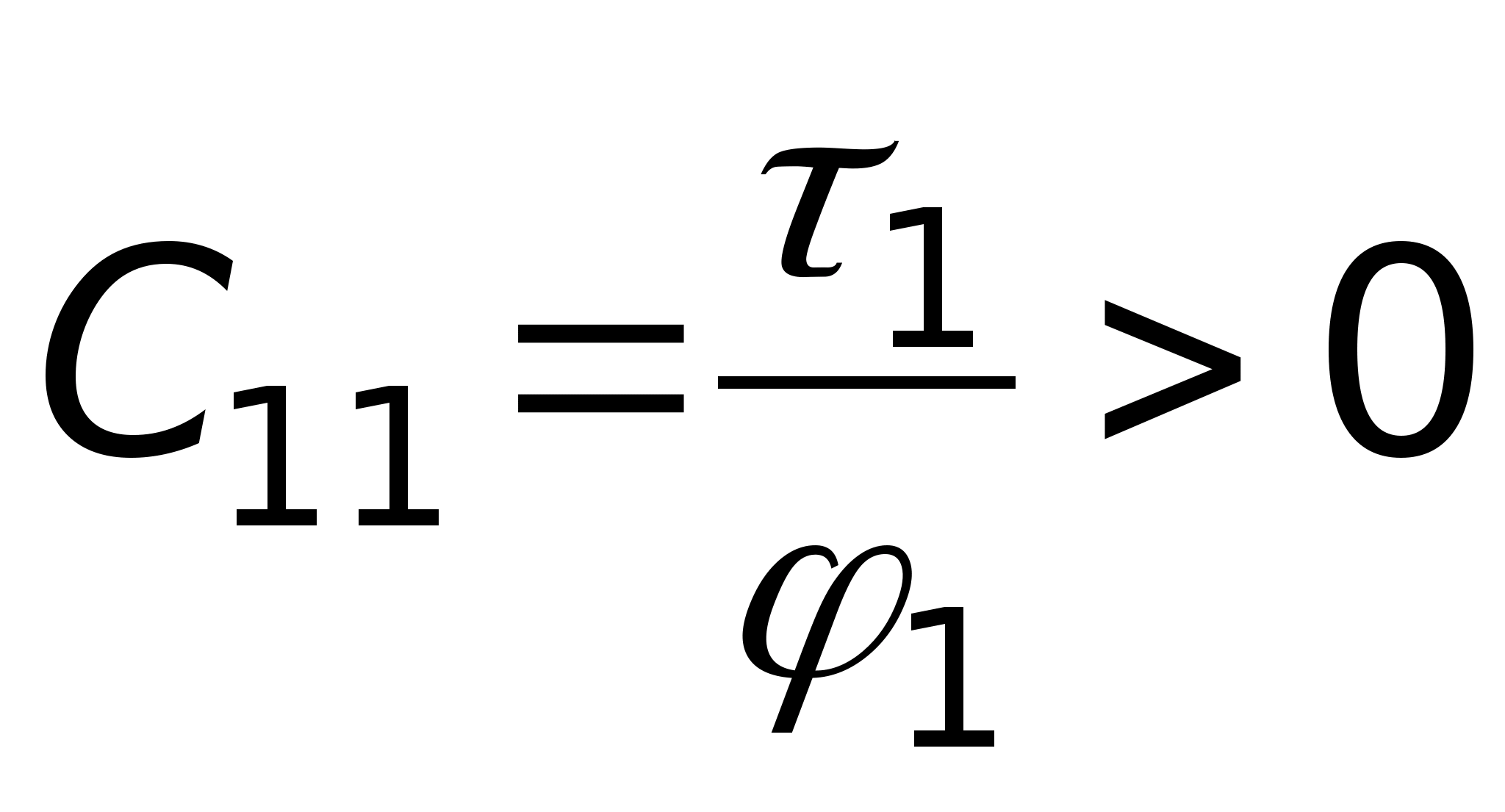 .
.
Własne wydajności cząstkowe można wyznaczyć doświadczalnie. Aby to zrobić wystarczy dokonać pomiaru po naładowaniu układu 1 i do obliczeń użyj ostatniego wzoru Z 11 . C km =- km nazywana wzajemną pojemnością częściową k i =0), a potencjał wszystkich punktów każdego przewodu jest taki sam, tj. powierzchnia każdego drutu jest ekwipotencjalna. Dlatego dwie naładowane osie zlokalizowane w tzw-th przewodniki, jest to również pozytywne, ponieważ km C km definiuje się również jako km .
D
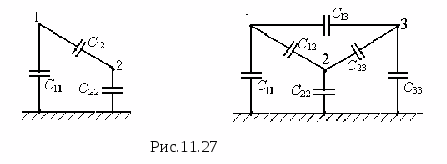 Aby wizualnie zilustrować wydajności częściowe, podajemy dwa przykłady. Będą to zestawy pojemności cząstkowych linii dwuprzewodowej i trójprzewodowej linii elektroenergetycznej (ryc. 11.27). Na podstawie tych agregatów można określić przepustowość eksploatacyjną linii. A więc dla dwuprzewodowej linii energetycznej
Aby wizualnie zilustrować wydajności częściowe, podajemy dwa przykłady. Będą to zestawy pojemności cząstkowych linii dwuprzewodowej i trójprzewodowej linii elektroenergetycznej (ryc. 11.27). Na podstawie tych agregatów można określić przepustowość eksploatacyjną linii. A więc dla dwuprzewodowej linii energetycznej
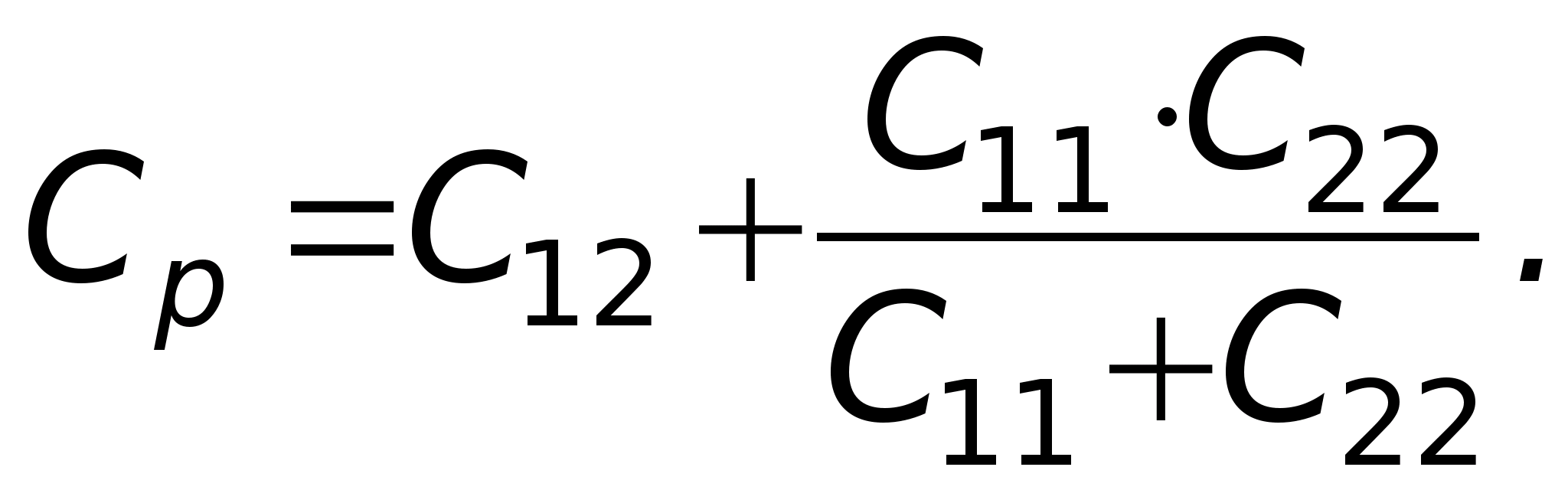
Pojemności cząstkowe oblicza się nie tylko dla pól elektrostatycznych, ale wykorzystuje się je także przy obliczaniu szybkich procesów (na przykład w lampach elektronowych i tranzystorach są to pojemności między ich elektrodami), a także przy obliczaniu urządzeń, których działanie opiera się na zastosowaniu pojemności cząstkowych (na przykład przy odbiorze mocy pojemnościowej z linii wysokiego napięcia).
Trzecia grupa wzorów Maxwella dla układu ciał naładowanych o dowolnym kształcie. Powyższe wzory na określenie współczynników potencjału obowiązują jednak tylko dla linii elektroenergetycznych. Jeśli ciała mają inny kształt, wówczas formuły będą inne. W przypadku ciał o skomplikowanym kształcie nie ma możliwości wyprowadzenia wzorów na współczynniki a następnie współczynniki pojemności wyznacza się eksperymentalnie.
Pole elektryczne prądu stałego w ośrodku przewodzącym
Ośrodek zawierający wolne ładunki nazywa się przewodzącym. Jeśli w takim środowisku wytworzymy pole elektryczne o natężeniu mi, a następnie za każdą z bezpłatnych opłat Q siła będzie działać 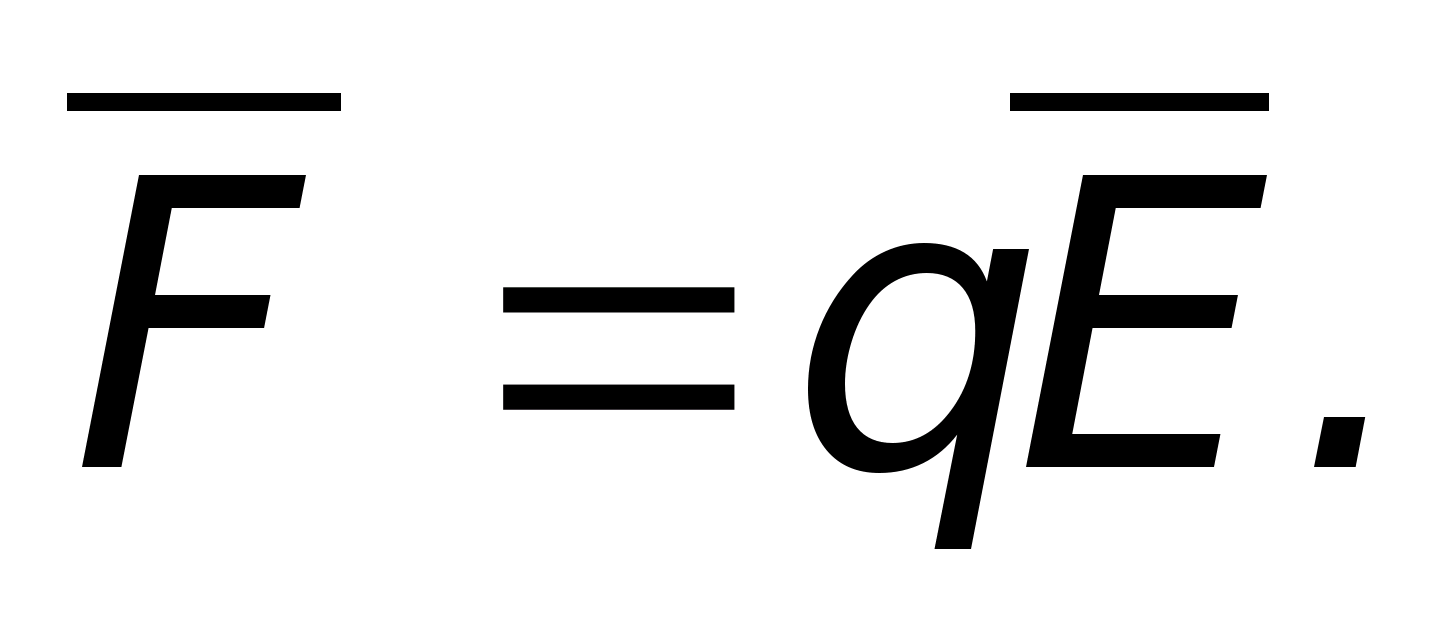 Pod wpływem tej siły swobodne ładunki zaczną się poruszać i to w uporządkowany sposób. Uporządkowany ruch cząstek przenoszących ładunki jest prądem. Zatem w ośrodku przewodzącym powstaje prąd, jeśli wytworzy się w nim pole elektryczne. W rzeczywistości istnieje kilka rodzajów prądu, a prąd przepływający przez ośrodek przewodzący nazywany jest zwykle prądem przewodzenia. Należy wspomnieć, że ładunki swobodne to elektrony w metalach i jony w cieczach i gazach. W procesie ruchu swobodne ładunki ulegają licznym zderzeniom z innymi cząsteczkami ciała będącymi w ruchu termicznym. Zderzenia te utrudniają uporządkowany ruch nośników ładunku i są przyczyną oporu, jaki ośrodek stawia przepływowi prądu. Gdyby tych zderzeń nie było, nie byłoby oporu, który występuje w nadprzewodnikach. Właściwość ośrodka określająca jego zdolność do przewodzenia prądu elektrycznego charakteryzuje się przewodnością właściwą
. Zależy ona od właściwości fizycznych materiału przewodzącego oraz od temperatury i jest mierzona w sm/m=1/Om *
M.
Pod wpływem tej siły swobodne ładunki zaczną się poruszać i to w uporządkowany sposób. Uporządkowany ruch cząstek przenoszących ładunki jest prądem. Zatem w ośrodku przewodzącym powstaje prąd, jeśli wytworzy się w nim pole elektryczne. W rzeczywistości istnieje kilka rodzajów prądu, a prąd przepływający przez ośrodek przewodzący nazywany jest zwykle prądem przewodzenia. Należy wspomnieć, że ładunki swobodne to elektrony w metalach i jony w cieczach i gazach. W procesie ruchu swobodne ładunki ulegają licznym zderzeniom z innymi cząsteczkami ciała będącymi w ruchu termicznym. Zderzenia te utrudniają uporządkowany ruch nośników ładunku i są przyczyną oporu, jaki ośrodek stawia przepływowi prądu. Gdyby tych zderzeń nie było, nie byłoby oporu, który występuje w nadprzewodnikach. Właściwość ośrodka określająca jego zdolność do przewodzenia prądu elektrycznego charakteryzuje się przewodnością właściwą
. Zależy ona od właściwości fizycznych materiału przewodzącego oraz od temperatury i jest mierzona w sm/m=1/Om *
M.
Główną wielkością charakteryzującą pole elektryczne w ośrodku przewodzącym (zwaną dalej polem w ośrodku przewodzącym) jest wektor gęstości prądu 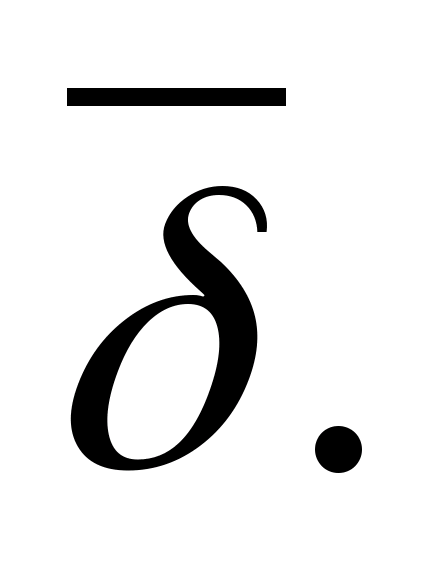 Jego kierunek jest taki sam jak wektor mi(wyraźnie z fizyki zjawisk) wielkość definiuje się jako
Jego kierunek jest taki sam jak wektor mi(wyraźnie z fizyki zjawisk) wielkość definiuje się jako 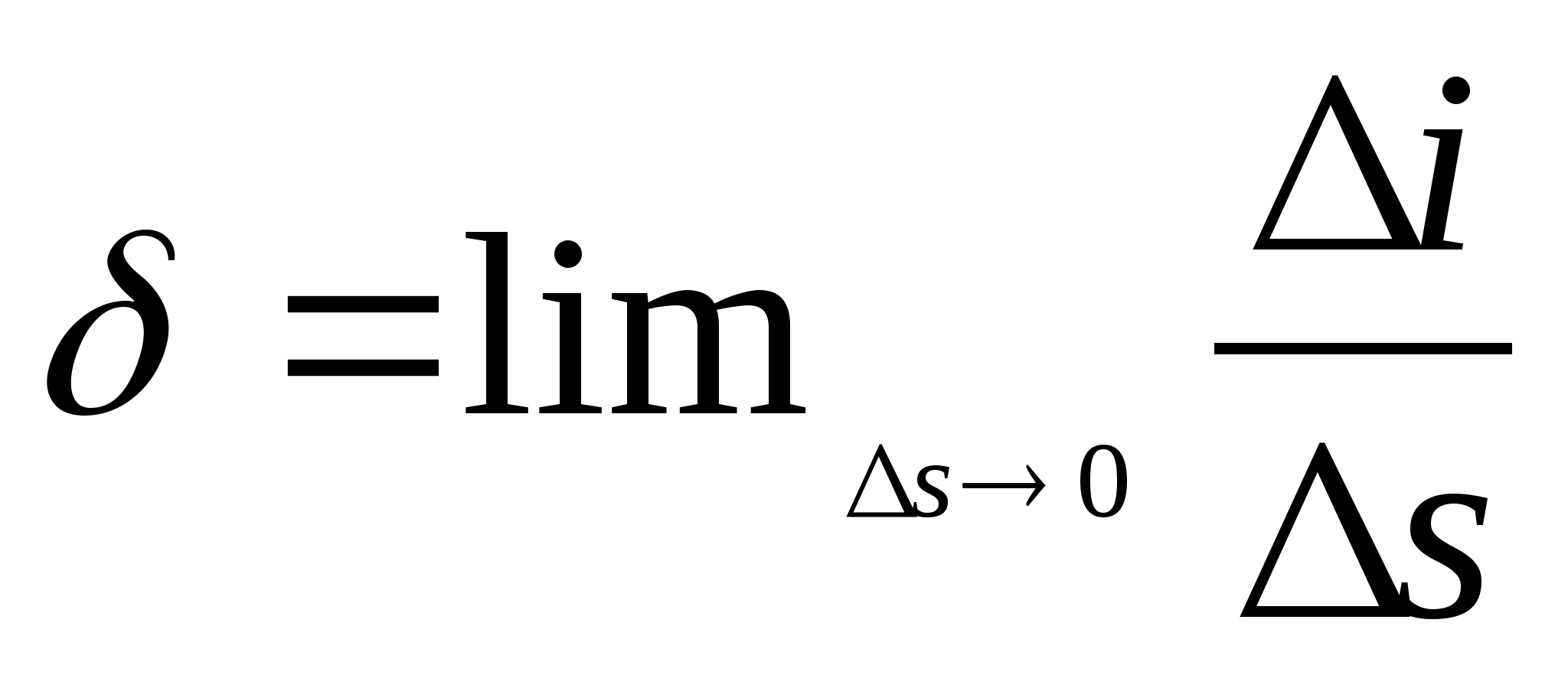 przy założeniu, że prąd elementarny I prostopadle do pola elementarnego S. Wymierzony
V Pojazd 2 .
przy założeniu, że prąd elementarny I prostopadle do pola elementarnego S. Wymierzony
V Pojazd 2 .
W teorii pola w ośrodku przewodzącym powszechnie stosuje się pojęcie prądu I, czyli przepływ wektora
:
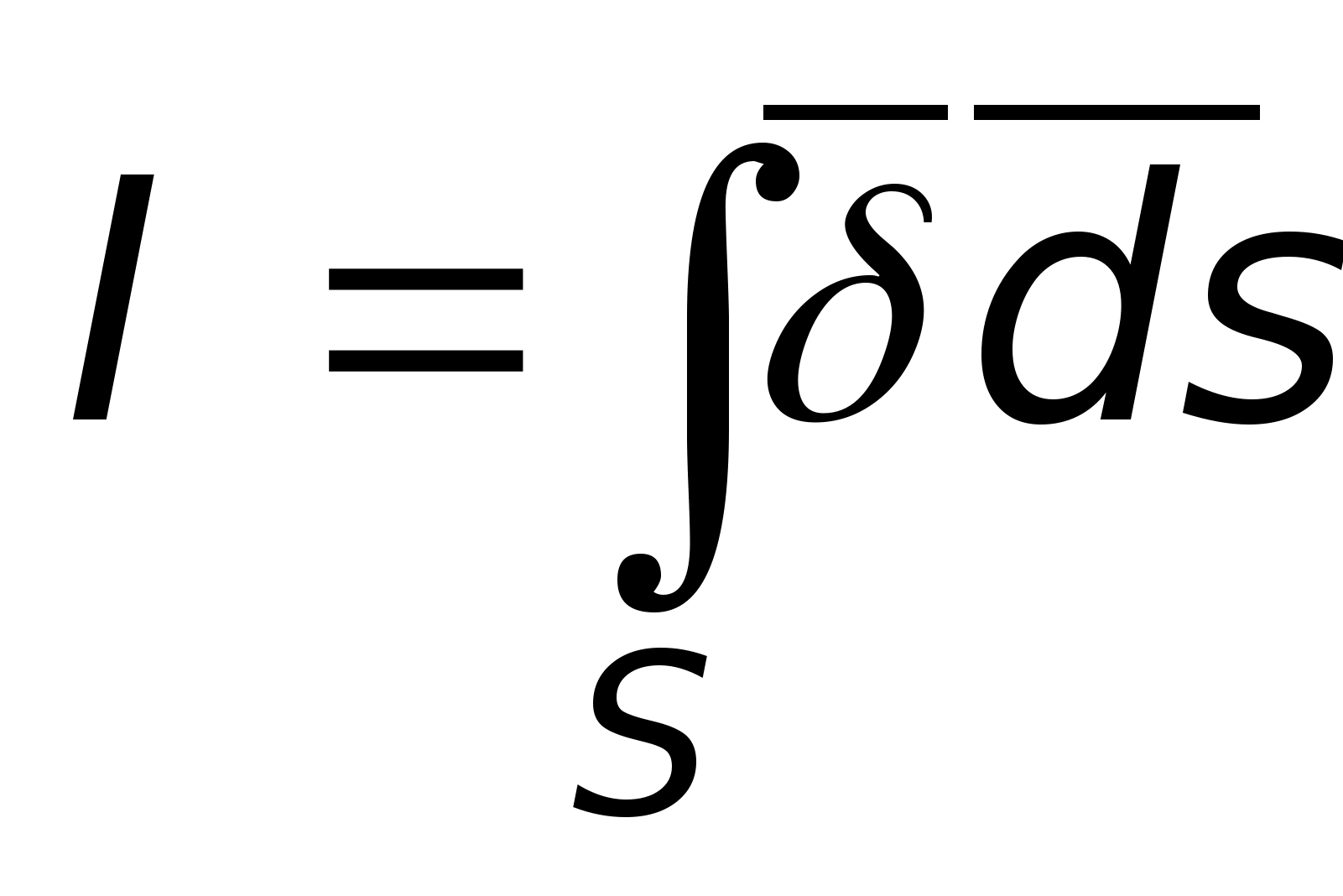 , Gdzie S- powierzchnia, przez którą wyznaczany jest prąd. Na wszelki wypadek
=stała i wektory
z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory pokrywają się w kierunku I=
S.
, Gdzie S- powierzchnia, przez którą wyznaczany jest prąd. Na wszelki wypadek
=stała i wektory
z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy jest skierowany w stronę normalnej zewnętrznej terenu (znajduje się w pobliżu rozpatrywanego punktu). Ponieważ w naszym przykładzie wektory pokrywają się w kierunku I=
S.
Prawa Ohma, Kirchhoffa i Joule'a-Lenza w postaci różniczkowej
W 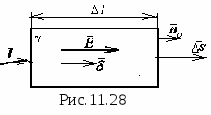 Odizolujmy mentalnie objętość od ośrodka przewodzącego V w postaci bardzo małego cylindra (ryc. 11.28). Niech jego długość l, przekrój S.
Odizolujmy mentalnie objętość od ośrodka przewodzącego V w postaci bardzo małego cylindra (ryc. 11.28). Niech jego długość l, przekrój S.
Ustawmy ten cylinder tak, aby jego tworząca pokrywała się z kierunkiem wektorów mi M
. Ze względu na małą objętość V możemy założyć, że wektory mi M
niezmieniona we wszystkich punktach. Następnie prąd płynący przez korpus cylindra: 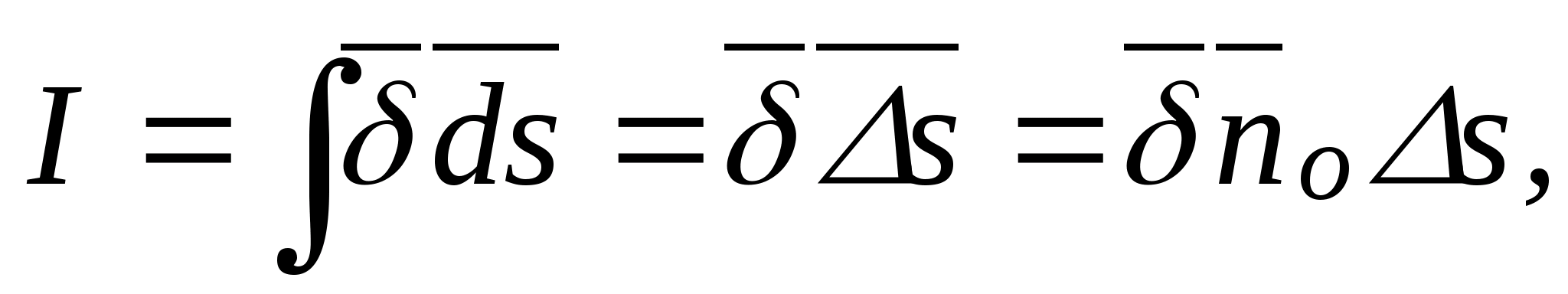 Gdzie
Gdzie 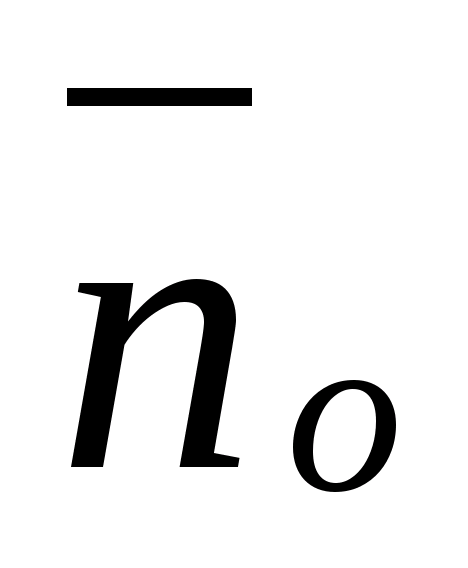 - wektor jednostkowy mający ten sam kierunek co wektory mi
,
i S. Naprężenie między podstawami cylindrów:
- wektor jednostkowy mający ten sam kierunek co wektory mi
,
i S. Naprężenie między podstawami cylindrów: 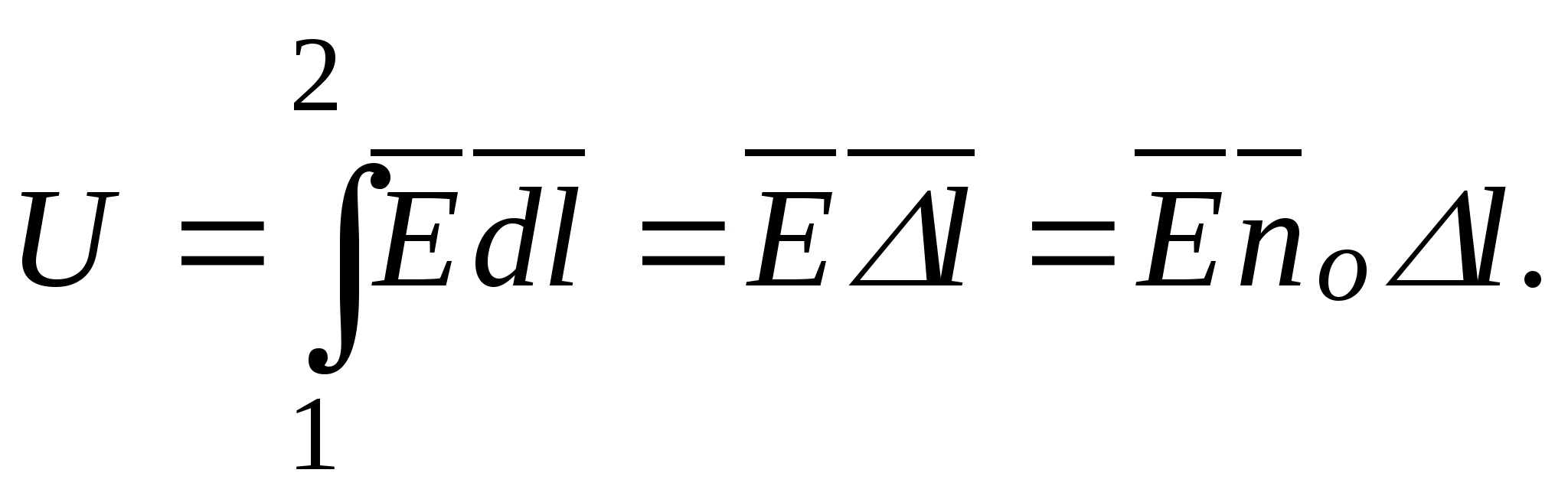 Cylindryczny opór objętościowy
Cylindryczny opór objętościowy 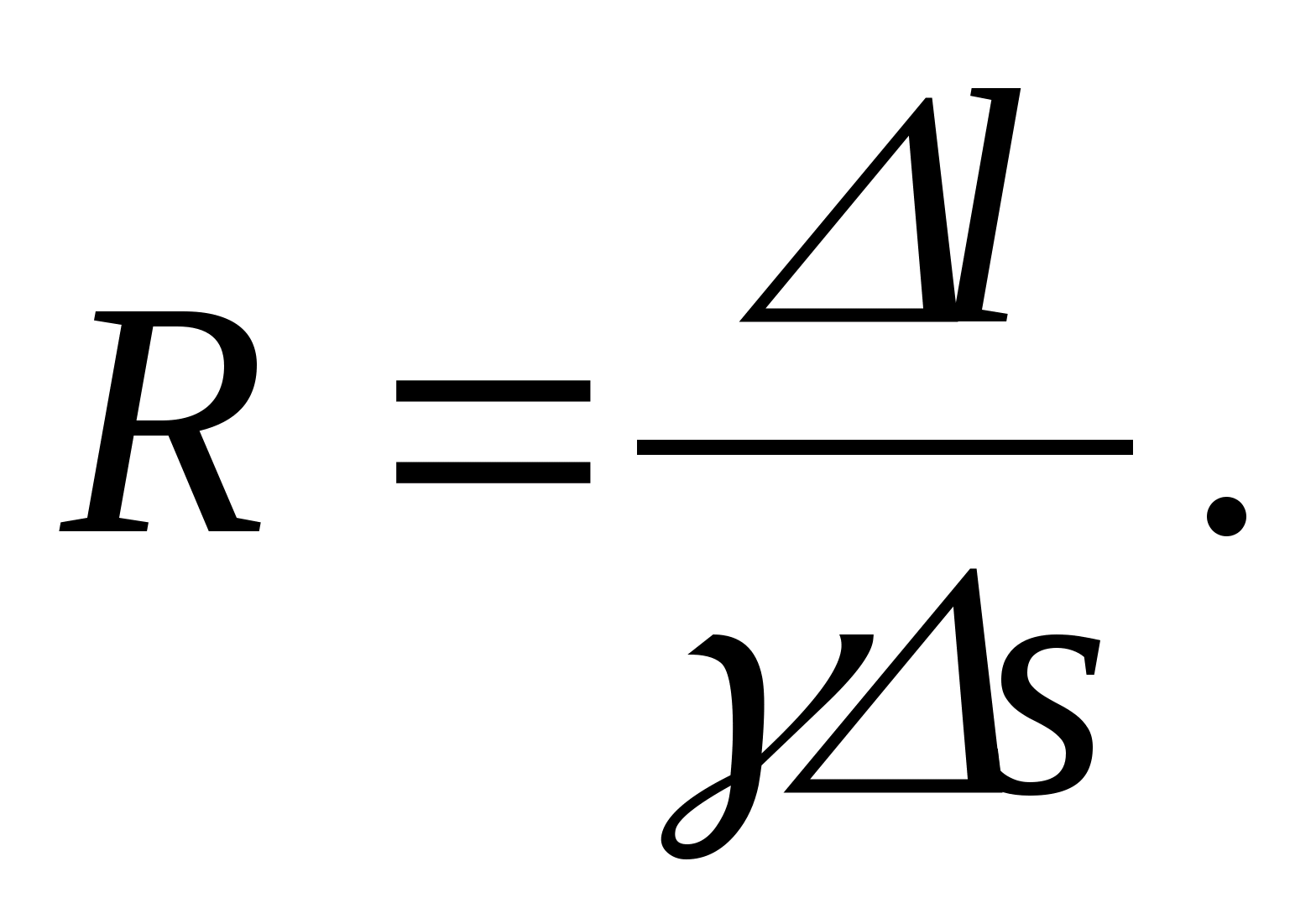 Zgodnie z prawem Ohma w postaci całkowej
Zgodnie z prawem Ohma w postaci całkowej 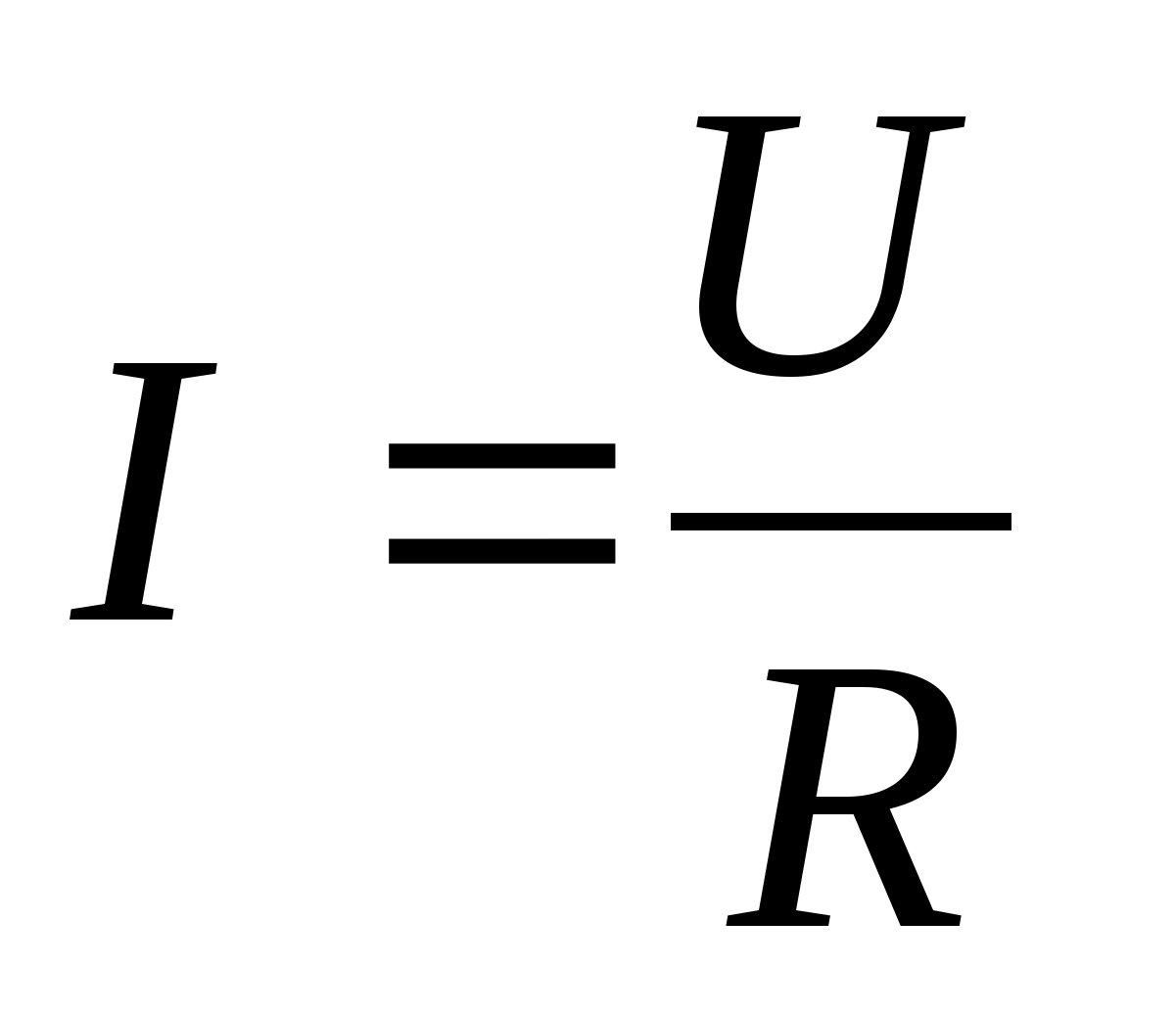 Lub
Lub 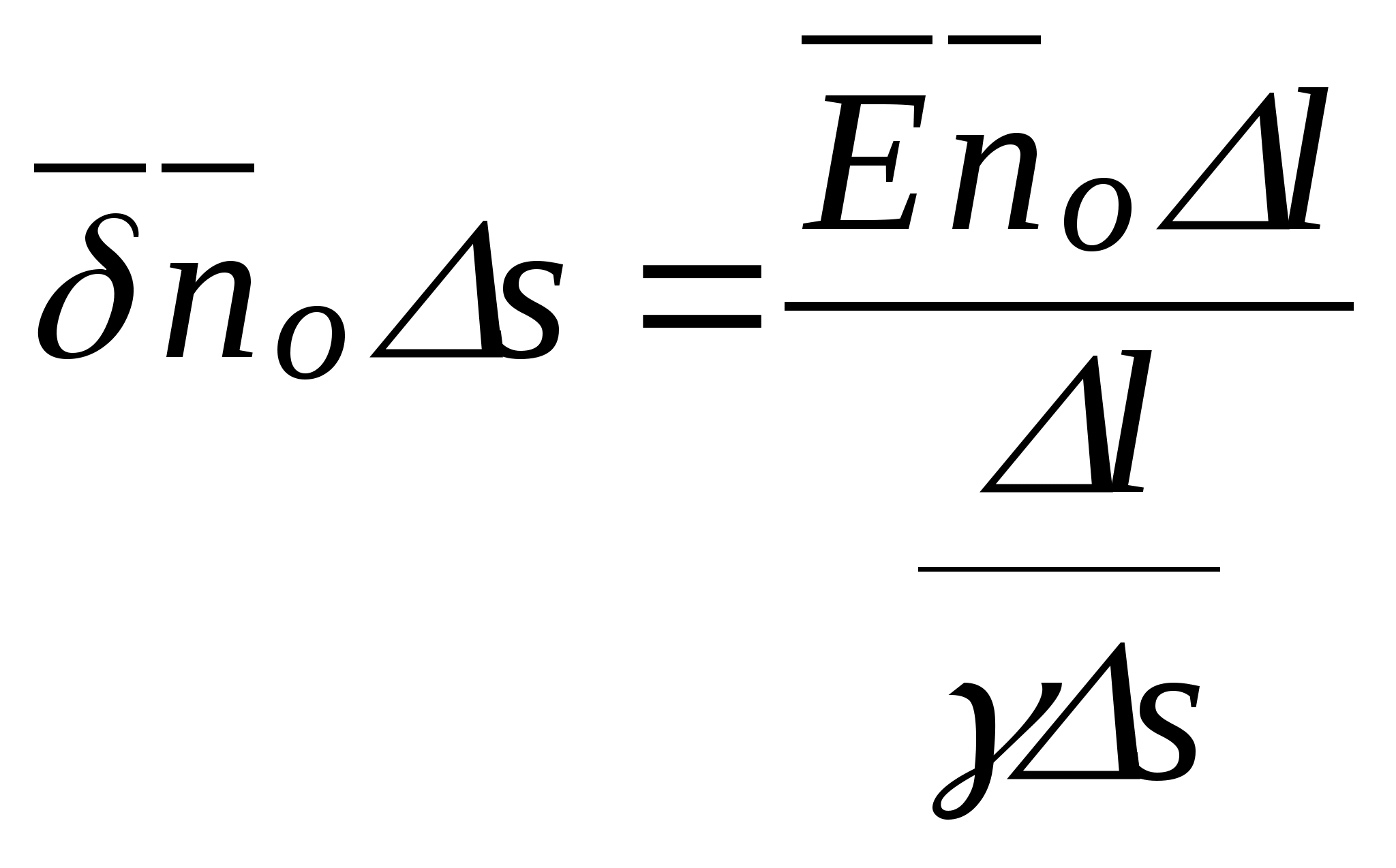 można pominąć ze względu na małą wielkość tych boków. Dla pola potencjalnego, które jest elektrostatyczne,
można pominąć ze względu na małą wielkość tych boków. Dla pola potencjalnego, które jest elektrostatyczne, 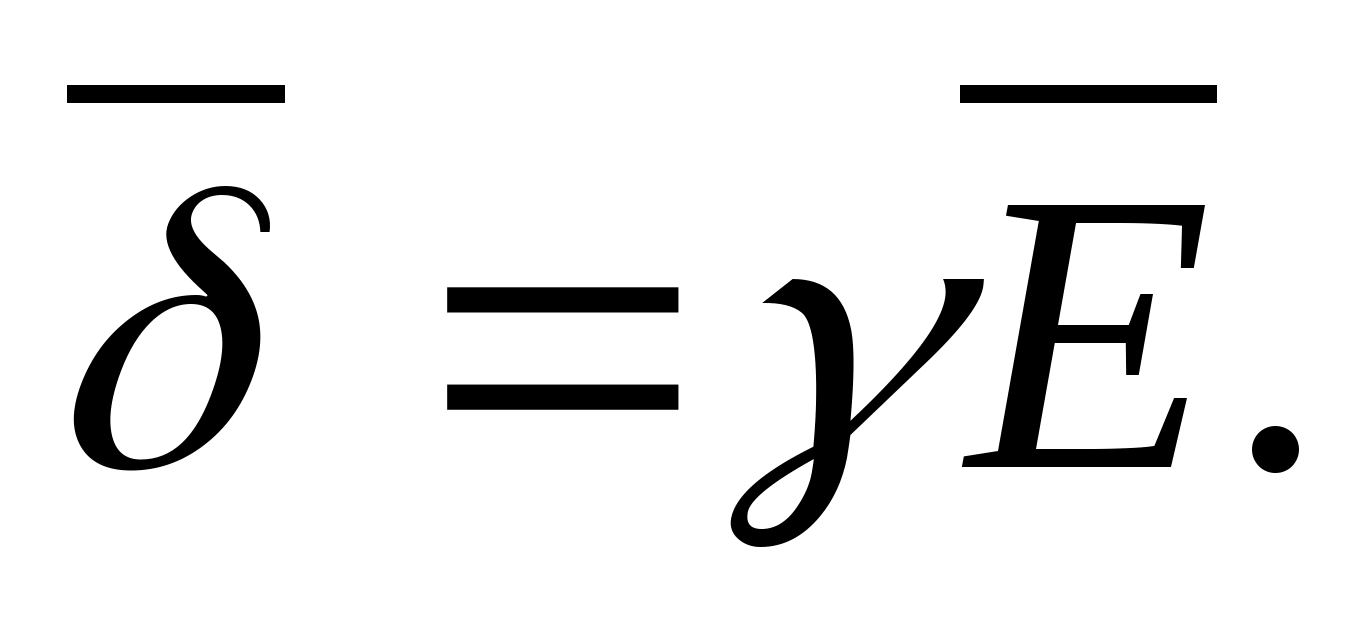 To jest prawo Ohma w postaci różniczkowej. Wyrażenie to nazywa się różniczkową formą całkowitego prawa prądu, ponieważ podaje punktową charakterystykę pola: w określonym punkcie wiąże gęstość prądu i natężenie pola. Wyrażenie to dotyczy obszarów pola niezajętych przez źródła pola elektromagnetycznego. A w obszarach zajmowanych przez źródła, oprócz pola „kulombowskiego” (elektrostatycznego), istnieje również tzw. Zewnętrzne pole elektryczne. Rzeczywiście wiemy, że jeśli przewodnik zostanie wprowadzony w pole elektrostatyczne, to będą się w nim poruszać swobodne ładunki. Co więcej, będą się poruszać tak bardzo, że utworzone przez nich pole całkowicie kompensuje pole zewnętrzne. Aby prąd płynął w przewodniku przez długi czas, konieczna jest obecność pola elektrycznego, którego siły będą w sposób ciągły przemieszczać swobodne ładunki. Takie pole może być wytworzone i utrzymywane przez siły pochodzenia nieelektrycznego (termoelektrycznego, chemicznego itp.), Innymi słowy, pole strony trzeciej jest zawsze powiązane ze źródłem energii, które zamienia część energii na energię elektryczną. Zewnętrzne natężenie pola mi sklep definiuje się jako granicę stosunku siły działającej na ładunek zmierzający do zera, pochodzącej z pola zewnętrznego, do wielkości tego ładunku. Jeśli zarówno „kulomb”, jak i pole zewnętrzne działają jednocześnie w przewodniku, wówczas siła powstałego pola będzie wynosić
To jest prawo Ohma w postaci różniczkowej. Wyrażenie to nazywa się różniczkową formą całkowitego prawa prądu, ponieważ podaje punktową charakterystykę pola: w określonym punkcie wiąże gęstość prądu i natężenie pola. Wyrażenie to dotyczy obszarów pola niezajętych przez źródła pola elektromagnetycznego. A w obszarach zajmowanych przez źródła, oprócz pola „kulombowskiego” (elektrostatycznego), istnieje również tzw. Zewnętrzne pole elektryczne. Rzeczywiście wiemy, że jeśli przewodnik zostanie wprowadzony w pole elektrostatyczne, to będą się w nim poruszać swobodne ładunki. Co więcej, będą się poruszać tak bardzo, że utworzone przez nich pole całkowicie kompensuje pole zewnętrzne. Aby prąd płynął w przewodniku przez długi czas, konieczna jest obecność pola elektrycznego, którego siły będą w sposób ciągły przemieszczać swobodne ładunki. Takie pole może być wytworzone i utrzymywane przez siły pochodzenia nieelektrycznego (termoelektrycznego, chemicznego itp.), Innymi słowy, pole strony trzeciej jest zawsze powiązane ze źródłem energii, które zamienia część energii na energię elektryczną. Zewnętrzne natężenie pola mi sklep definiuje się jako granicę stosunku siły działającej na ładunek zmierzający do zera, pochodzącej z pola zewnętrznego, do wielkości tego ładunku. Jeśli zarówno „kulomb”, jak i pole zewnętrzne działają jednocześnie w przewodniku, wówczas siła powstałego pola będzie wynosić 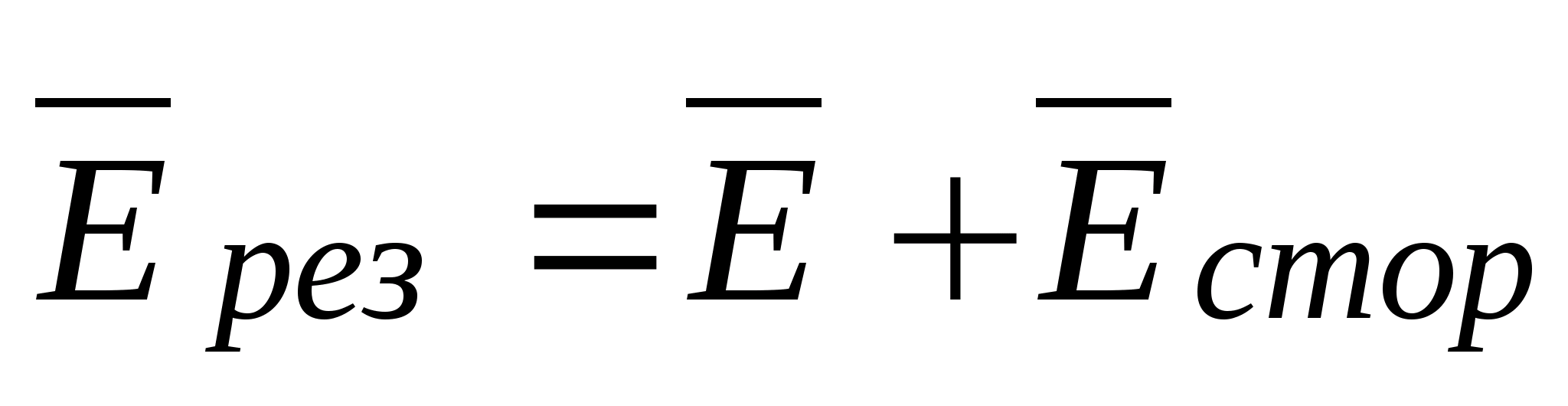 . I wtedy wyrażenie prawa Ohma przybiera formę
. I wtedy wyrażenie prawa Ohma przybiera formę 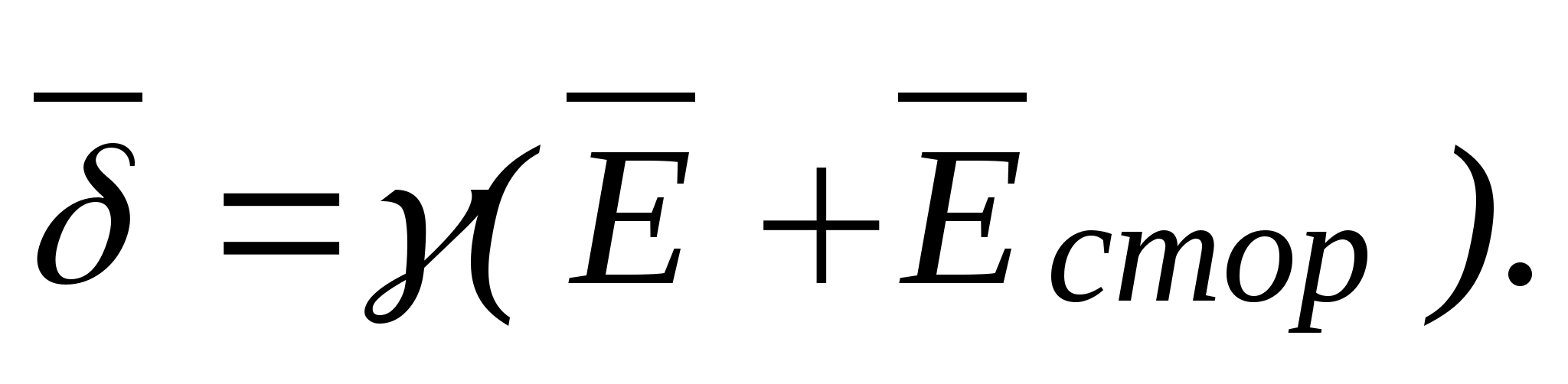 Wyrażenie to nazywa się uogólnionym prawem Ohma w formie różniczkowej lub drugim prawem Kirchhoffa.
Wyrażenie to nazywa się uogólnionym prawem Ohma w formie różniczkowej lub drugim prawem Kirchhoffa.
Jeśli w ośrodku przewodzącym wybierzemy pewną zamkniętą objętość, przez którą przepływa prąd stały, wówczas jasne jest, że prąd wpływający do tej objętości musi być równy prądowi, który ją opuszcza; w przeciwnym razie nastąpi akumulacja lub redukcja ładunków elektrycznych w tym tomie, co nie jest potwierdzone doświadczeniem. Innymi słowy, suma prądów wchodzących i wychodzących z objętości wynosi zero, co matematycznie zapisuje się w następujący sposób 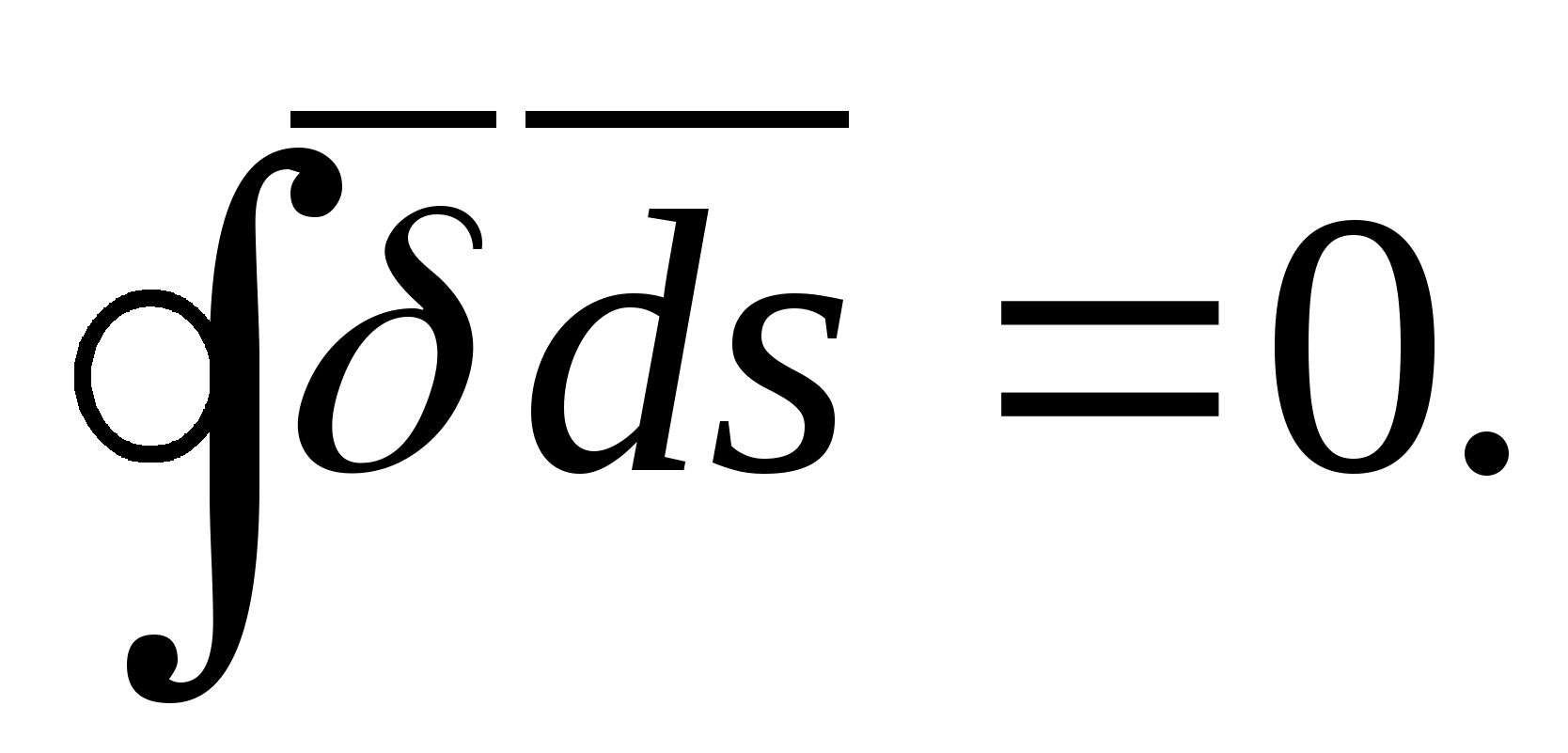 Zależność ta pozostanie ważna, jeśli przyjmiemy granicę stosunku strumienia wektora do objętości dążącej do zera, ograniczonej powierzchnią całkowania
Zależność ta pozostanie ważna, jeśli przyjmiemy granicę stosunku strumienia wektora do objętości dążącej do zera, ograniczonej powierzchnią całkowania 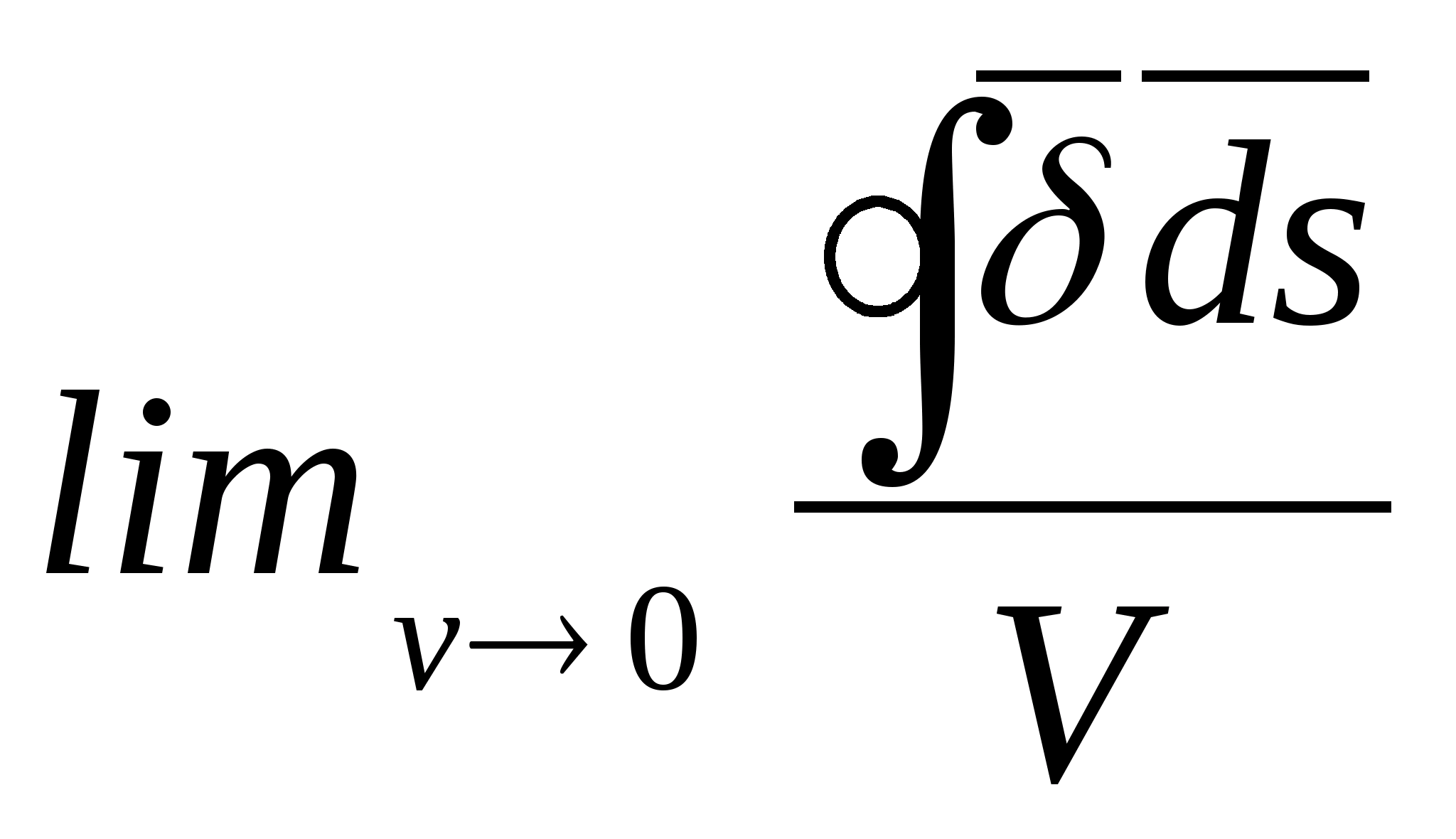 można pominąć ze względu na małą wielkość tych boków. Dla pola potencjalnego, które jest elektrostatyczne,
można pominąć ze względu na małą wielkość tych boków. Dla pola potencjalnego, które jest elektrostatyczne, 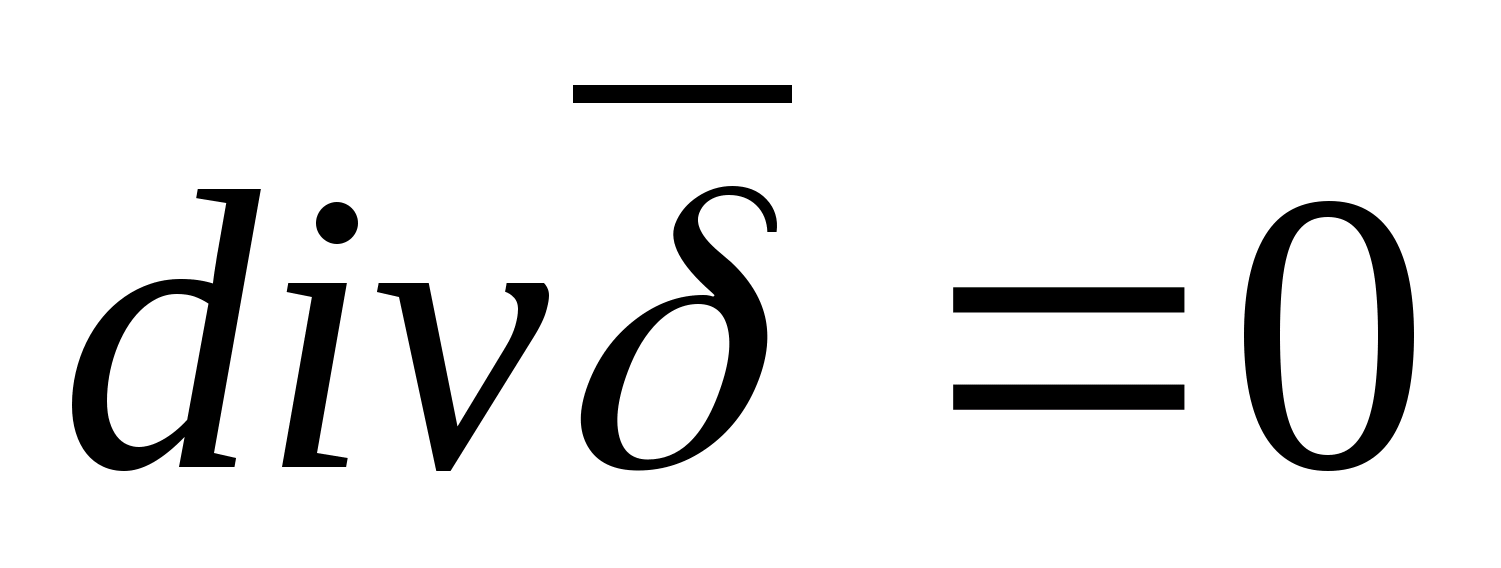 . Wyrażenie to nazywa się pierwszym prawem Kirchhoffa w postaci różniczkowej. Równanie to mówi, że w dowolnym punkcie pola w ośrodku przewodzącym nie ma ani drenażu, ani źródła linii wektorowych
lub linie wektorowe
są liniami ciągłymi zamkniętymi w sobie. Dlatego równanie to nazywane jest również równaniem ciągłości linii wektorowych
.
. Wyrażenie to nazywa się pierwszym prawem Kirchhoffa w postaci różniczkowej. Równanie to mówi, że w dowolnym punkcie pola w ośrodku przewodzącym nie ma ani drenażu, ani źródła linii wektorowych
lub linie wektorowe
są liniami ciągłymi zamkniętymi w sobie. Dlatego równanie to nazywane jest również równaniem ciągłości linii wektorowych
.
Jeśli wzdłuż dowolnego przewodnika z oporem R przepływ prądu stałego I, uwalnia moc P=I 2 R. Określmy moc uwalnianą na jednostkę objętości ośrodka przewodzącego 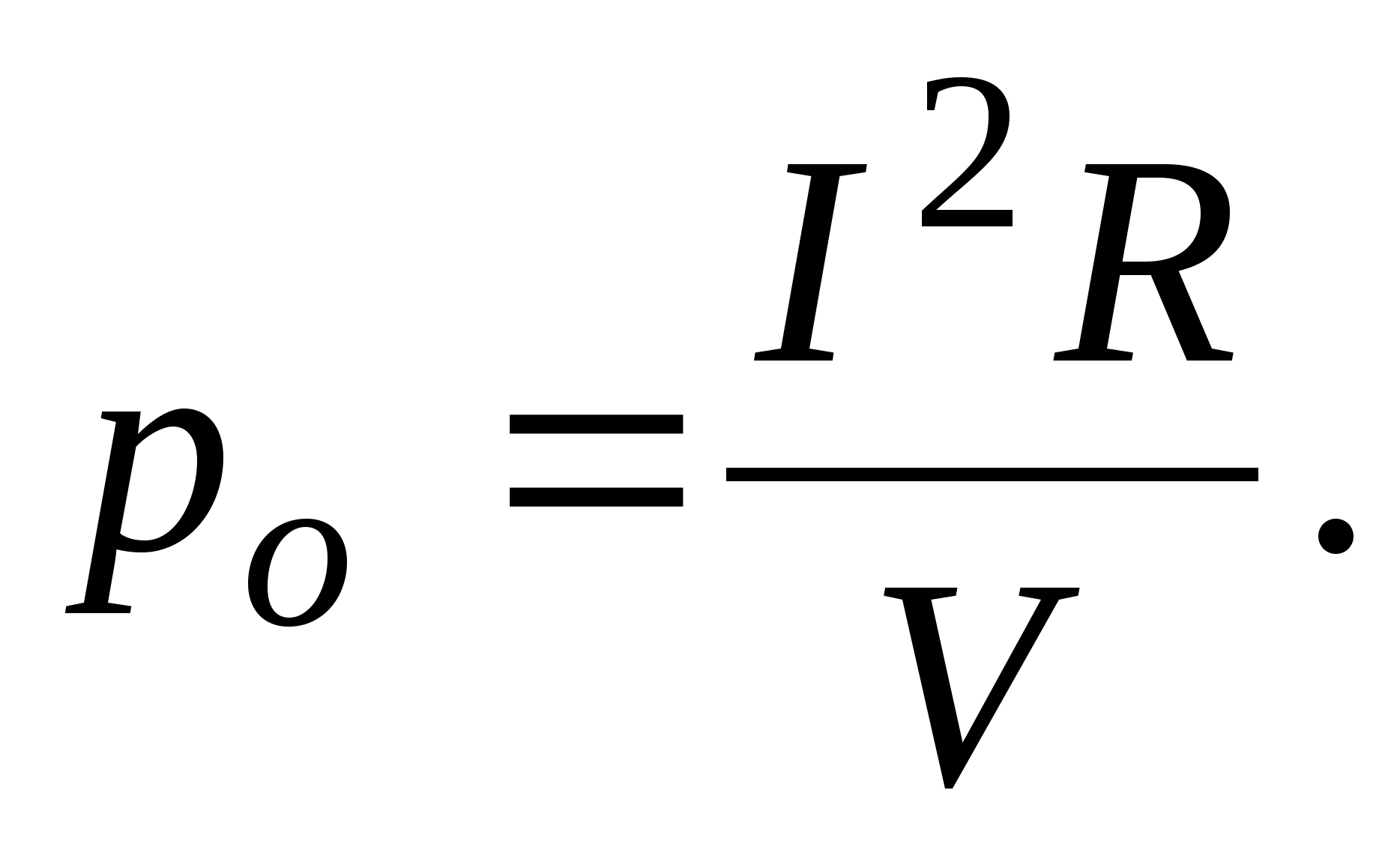 Jako wolumin V Weźmy cylinder Ryc. 11.28. W tym cylindrze
Jako wolumin V Weźmy cylinder Ryc. 11.28. W tym cylindrze 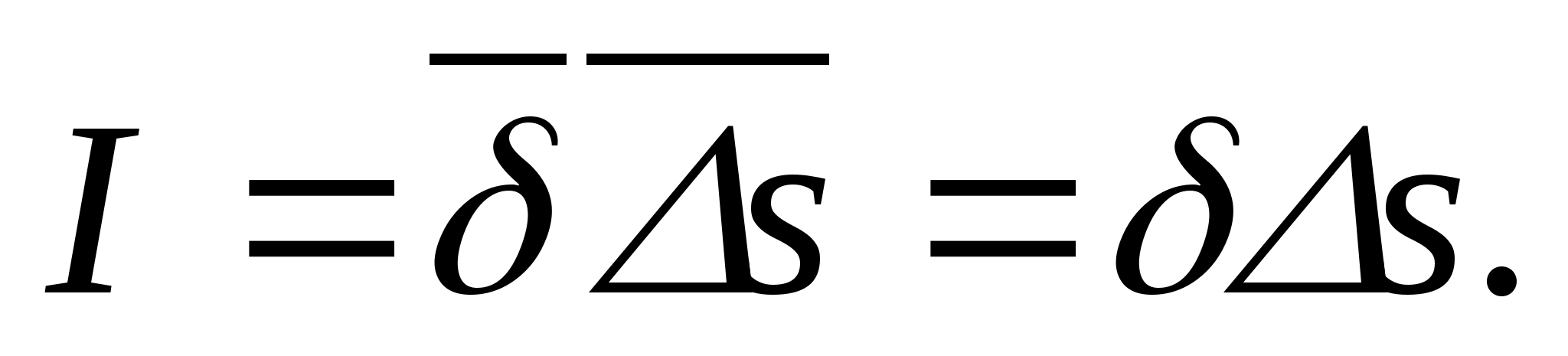 . Jego opór
. Jego opór 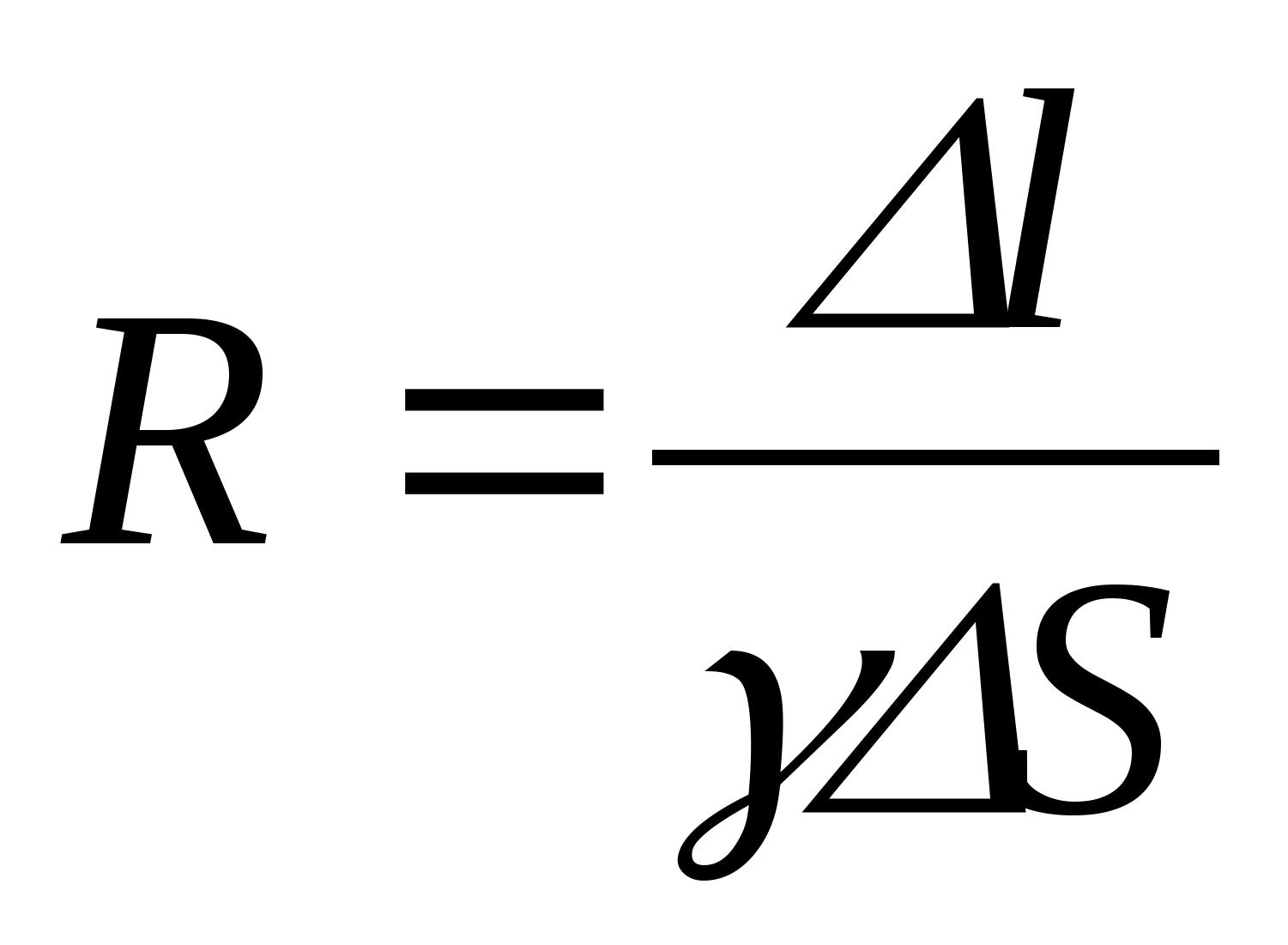 i głośność
i głośność 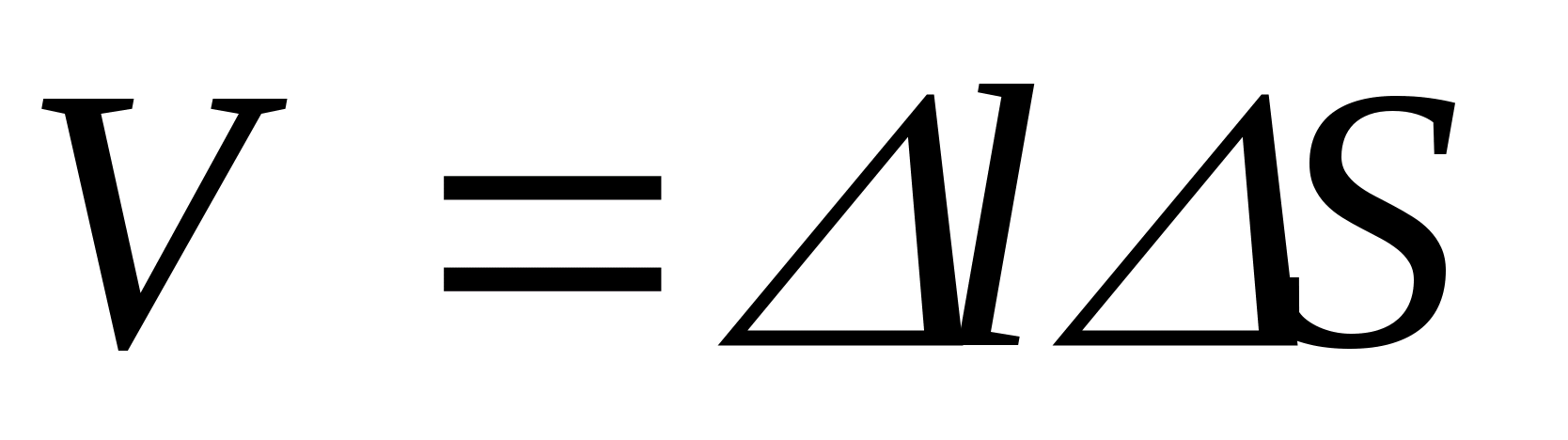 . W ramach przydzielonego wolumenu nie występują bezpłatne opłaty, tj.
. W ramach przydzielonego wolumenu nie występują bezpłatne opłaty, tj. 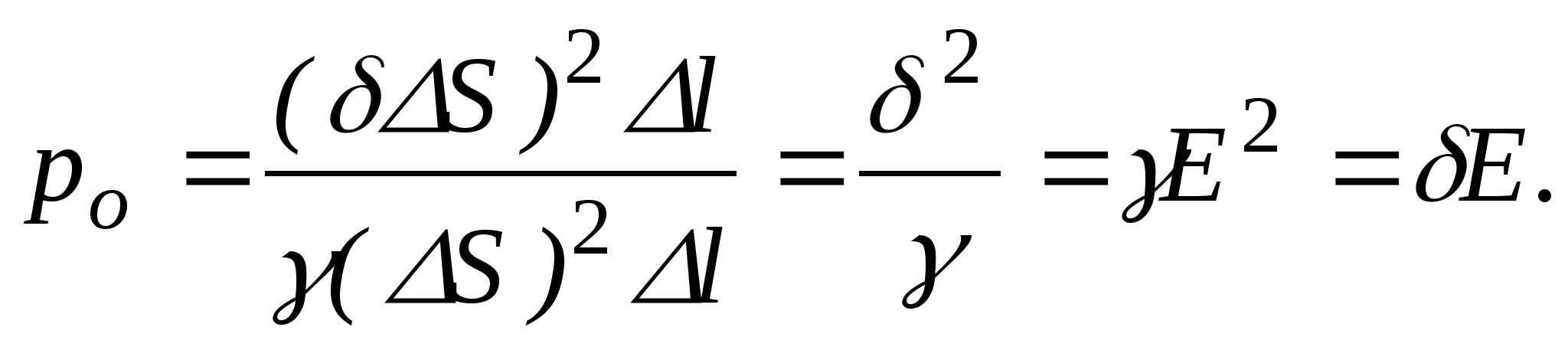 Jest to prawo Joule’a-Lenza w postaci różniczkowej. Moc strat ciepła w objętości o skończonych wymiarach można wyznaczyć ze wzoru
Jest to prawo Joule’a-Lenza w postaci różniczkowej. Moc strat ciepła w objętości o skończonych wymiarach można wyznaczyć ze wzoru 
Warunki brzegowe w polu w ośrodku przewodzącym
W  Dowiedzmy się, jakie warunki są spełnione, gdy prąd przepływa z ośrodka o jednej określonej przewodności do ośrodka o innej przewodności. Na granicy oddzielającej dwa różne ośrodki przewodzące spełnione są dwa warunki, które sformułujemy w jednym zdaniu: dla wszystkich punktów wspólnych dla tych ośrodków składowe styczne wektora są równe pod względem wielkości mi i normalne składowe wektora
. Aby udowodnić pierwszy warunek, otoczmy dowolny punkt znajdujący się na granicy ośrodków nieskończenie małą (długość - dł) płaski (wysokość jest nieskończenie mała w porównaniu z długością) kontur Pokażmy zasadność pierwszego warunku, dla którego bierzemy dowolny punkt na styku dwóch różnych dielektryków i otaczamy go nieskończenie małą (długość - i ułóż wyrażenie na cyrkulację wektora mi dla tego obwodu (ryc. 11.29). Strona wzdłuż tego konturu. Strona znajduje się w górnym środowisku i jeśli obrys jest zgodny z ruchem wskazówek zegara, wówczas składnik cyrkulacji jest podobny po tej stronie. Przez ściany boczne przepływ wektora można pominąć ze względu na małą wielkość tych ścian, a przez górę i dół - odpowiednio
Dowiedzmy się, jakie warunki są spełnione, gdy prąd przepływa z ośrodka o jednej określonej przewodności do ośrodka o innej przewodności. Na granicy oddzielającej dwa różne ośrodki przewodzące spełnione są dwa warunki, które sformułujemy w jednym zdaniu: dla wszystkich punktów wspólnych dla tych ośrodków składowe styczne wektora są równe pod względem wielkości mi i normalne składowe wektora
. Aby udowodnić pierwszy warunek, otoczmy dowolny punkt znajdujący się na granicy ośrodków nieskończenie małą (długość - dł) płaski (wysokość jest nieskończenie mała w porównaniu z długością) kontur Pokażmy zasadność pierwszego warunku, dla którego bierzemy dowolny punkt na styku dwóch różnych dielektryków i otaczamy go nieskończenie małą (długość - i ułóż wyrażenie na cyrkulację wektora mi dla tego obwodu (ryc. 11.29). Strona wzdłuż tego konturu. Strona znajduje się w górnym środowisku i jeśli obrys jest zgodny z ruchem wskazówek zegara, wówczas składnik cyrkulacji jest podobny po tej stronie. Przez ściany boczne przepływ wektora można pominąć ze względu na małą wielkość tych ścian, a przez górę i dół - odpowiednio
Ze swej natury pole elektrostatyczne i pole DC w ośrodku przewodzącym są zupełnie inne. Pole elektrostatyczne tworzą ładunki nieruchome i niezmienne w czasie, natomiast pole w ośrodku przewodzącym to pole ładunków, które pod wpływem zewnętrznego źródła nakazały ruch. Niemniej jednak pomiędzy tymi dwoma dziedzinami można przeprowadzić formalną analogię, która wygląda następująco.
1. Pole elektrostatyczne w obszarach niezajętych przez ładunek oraz pole w ośrodku przewodzącym w obszarach wolnych od źródeł pola elektromagnetycznego opisuje to samo równanie - równanie Laplace'a. Pokazaliśmy to już w przypadku pola elektrostatycznego
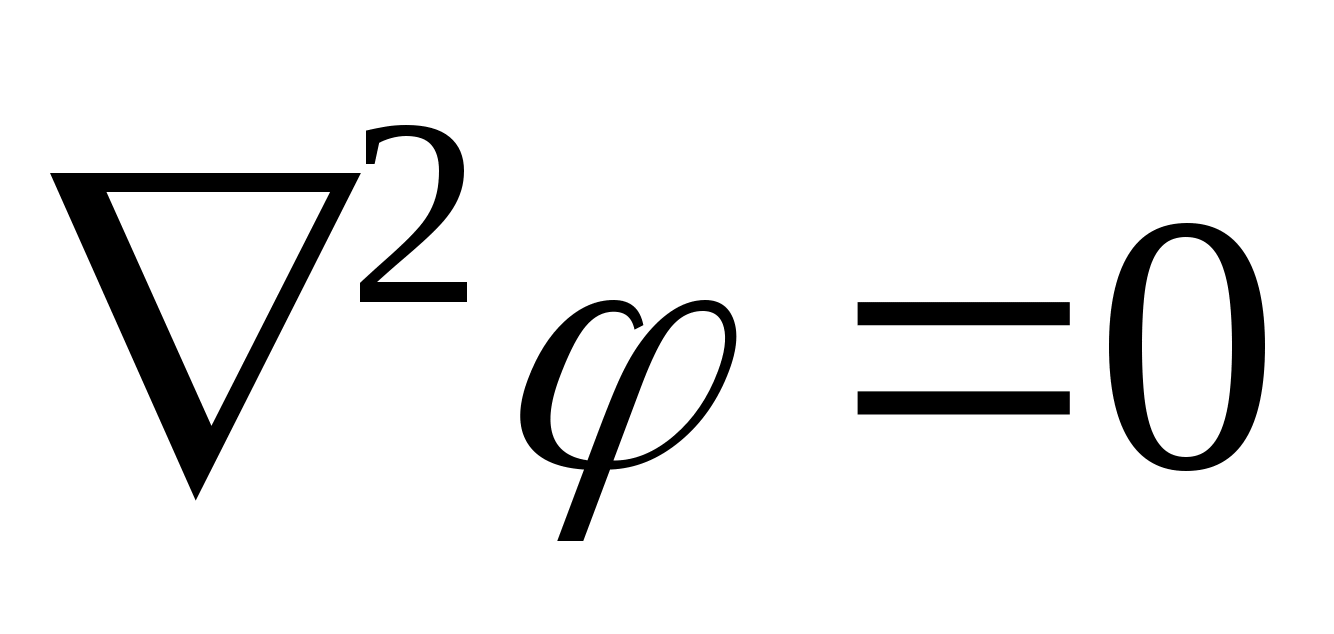 .
Pokażmy to dla pola w ośrodku przewodzącym, w którym
.
Pokażmy to dla pola w ośrodku przewodzącym, w którym 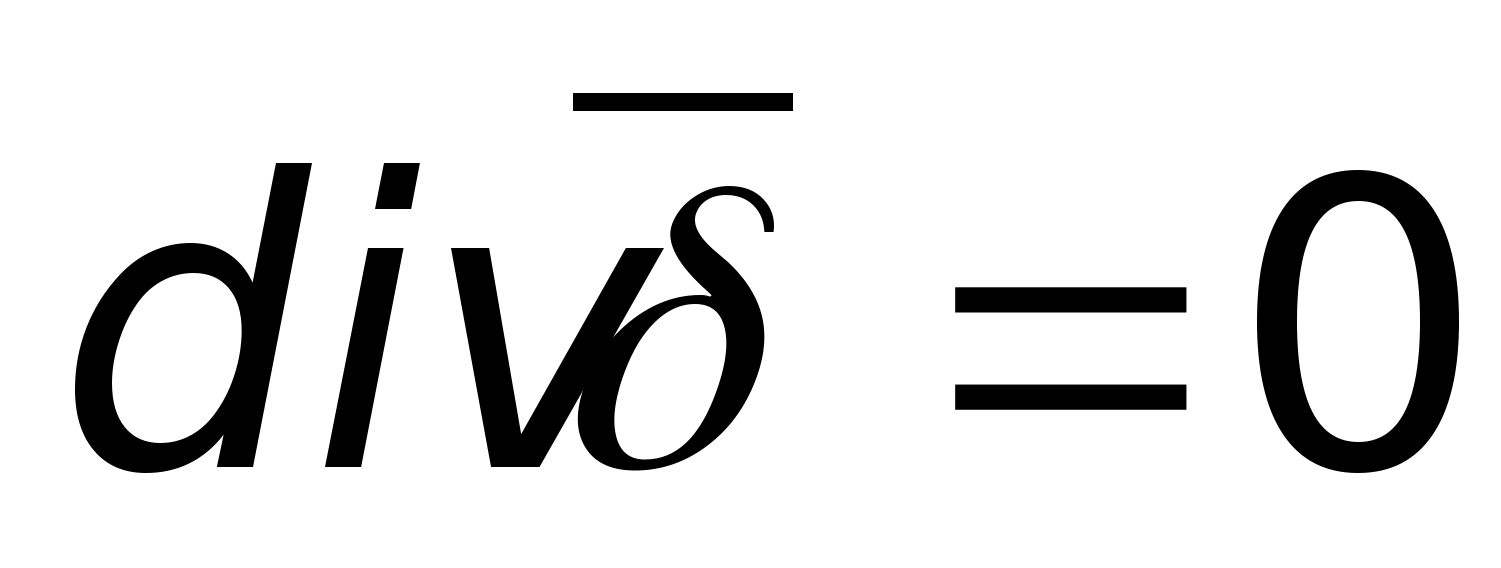 i Następnie
i Następnie 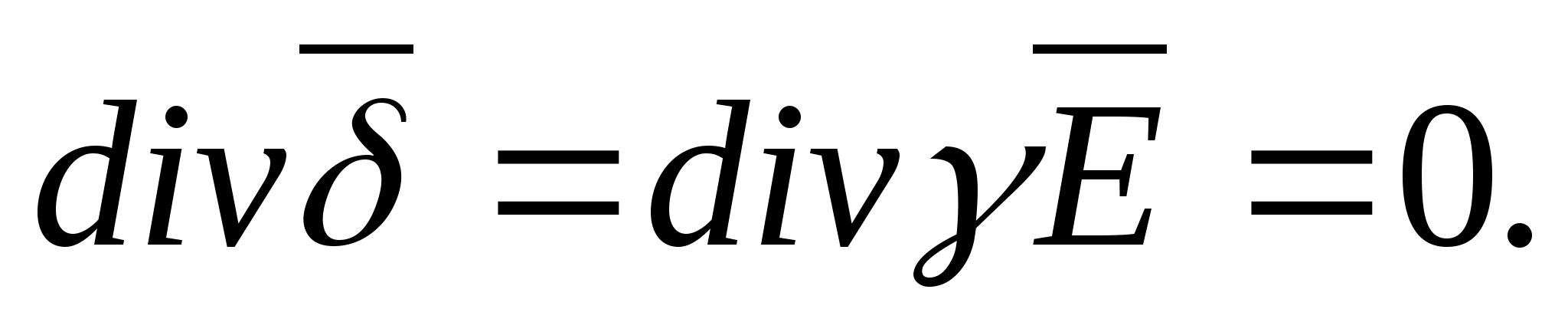 Jeśli ośrodek jest jednorodny i izotropowy, to jest wartością stałą, można to odjąć od znaku rozbieżności, który powinien dać zero, tj.
Jeśli ośrodek jest jednorodny i izotropowy, to jest wartością stałą, można to odjąć od znaku rozbieżności, który powinien dać zero, tj.
3. W tych polach dla podobnych wielkości spełnione są te same warunki brzegowe: w elektrostatyce mi 1 Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru ( =E 2 Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru ( M Co ciekawe, przepływ wektorowy 1 stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. 1n 2 stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. w ośrodku przewodzącym mi 1 Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru ( =E 2 Na takiej granicy spełnione są dwa warunki: dla wszystkich punktów dielektryka bezpośrednio przylegających do powierzchni przewodnika składowa styczna natężenia pola jest równa zeru ( M 1 stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. = 2 stworzy taki sam obraz pola, jak dwuprzewodowa linia energetyczna, jeśli tak jest. .
N 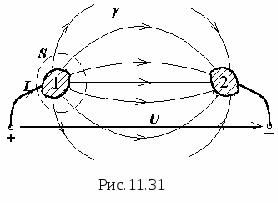 o jeśli dwa pola spełniają to samo równanie i te same warunki brzegowe dla podobnych wielkości są spełnione, to pola są identyczne, tj. mają te same zestawy sił i linii ekwipotencjalnych o tym samym kształcie powierzchni granicznych. Ta formalna analogia jest bardzo szeroko stosowana w praktyce. Zatem, jeśli zbadano jakiekolwiek pole elektrostatyczne, wówczas wszystkie informacje na jego temat można przenieść do geometrycznie podobnego pola w ośrodku przewodzącym. Oczywiście transfer odwrotny również jest prawdziwy. Ta analogia leży u podstaw modelowania jednych pól przez inne (najczęściej pola elektrostatyczne – pole w ośrodku przewodzącym). Analogia ta pozwala na wykorzystanie wzorów uzyskanych przy obliczaniu pól elektrostatycznych w przypadku pola w ośrodku przewodzącym. W szczególności wzory na przewodność między elektrodami umieszczonymi w ośrodku przewodzącym można otrzymać ze wzorów na pojemność między tymi samymi elektrodami w polu elektrostatycznym. Pokażmy to. Jeśli dwie elektrody zostaną umieszczone w ośrodku przewodzącym i zasilanie będzie do nich doprowadzane ze źródła napięcia NAS. Następnie zgodnie z twierdzeniem Gaussa w postaci całkowej
o jeśli dwa pola spełniają to samo równanie i te same warunki brzegowe dla podobnych wielkości są spełnione, to pola są identyczne, tj. mają te same zestawy sił i linii ekwipotencjalnych o tym samym kształcie powierzchni granicznych. Ta formalna analogia jest bardzo szeroko stosowana w praktyce. Zatem, jeśli zbadano jakiekolwiek pole elektrostatyczne, wówczas wszystkie informacje na jego temat można przenieść do geometrycznie podobnego pola w ośrodku przewodzącym. Oczywiście transfer odwrotny również jest prawdziwy. Ta analogia leży u podstaw modelowania jednych pól przez inne (najczęściej pola elektrostatyczne – pole w ośrodku przewodzącym). Analogia ta pozwala na wykorzystanie wzorów uzyskanych przy obliczaniu pól elektrostatycznych w przypadku pola w ośrodku przewodzącym. W szczególności wzory na przewodność między elektrodami umieszczonymi w ośrodku przewodzącym można otrzymać ze wzorów na pojemność między tymi samymi elektrodami w polu elektrostatycznym. Pokażmy to. Jeśli dwie elektrody zostaną umieszczone w ośrodku przewodzącym i zasilanie będzie do nich doprowadzane ze źródła napięcia NAS. Następnie zgodnie z twierdzeniem Gaussa w postaci całkowej 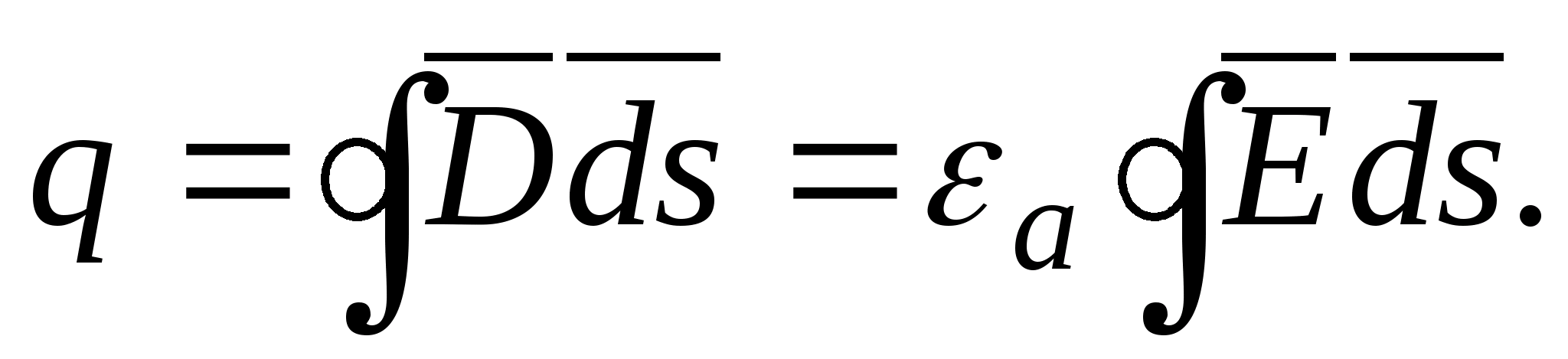 A
A 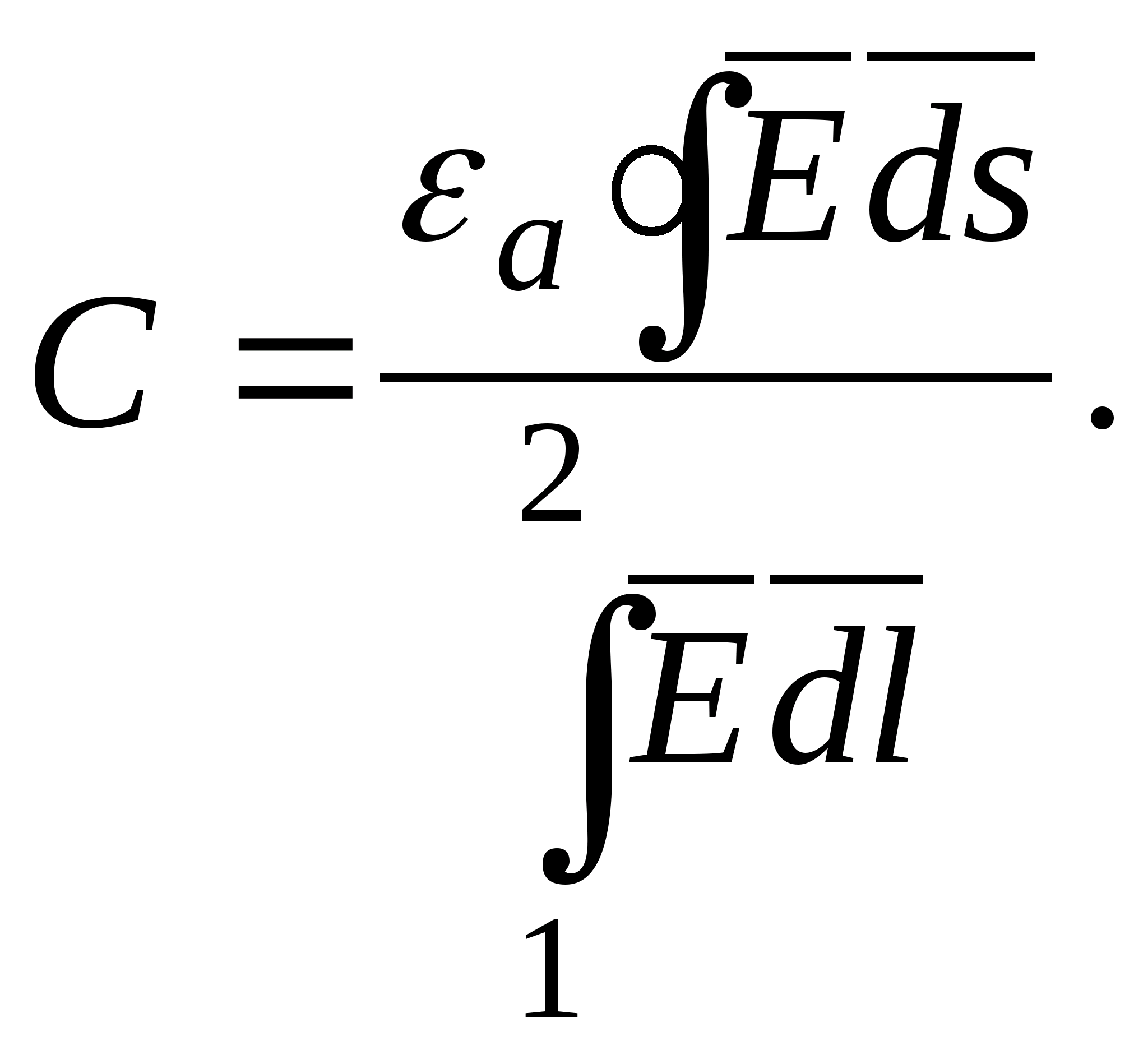
Z  wyrażenia wyrównujące dla G z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy Z, widzimy, że różnią się one tym, że w nich i zmieniają miejsca. Zależność tę można zapisać następująco
wyrażenia wyrównujące dla G z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy Z, widzimy, że różnią się one tym, że w nich i zmieniają miejsca. Zależność tę można zapisać następująco  co oznacza, że jeśli we wzorze na pojemność
A zastąpić przez
, wówczas otrzymujemy wzór na określenie G. Oczywiście możliwe jest również przejście odwrotne.
co oznacza, że jeśli we wzorze na pojemność
A zastąpić przez
, wówczas otrzymujemy wzór na określenie G. Oczywiście możliwe jest również przejście odwrotne.
R  Spójrzmy na konkretny przykład. Izolacja kabla koncentrycznego nigdy nie jest idealna. W praktyce ma pewną, choć bardzo niską, przewodność właściwą
. W związku z tym, jeśli do kabla zostanie przyłożone napięcie U, wówczas prąd zacznie zamykać się w izolacji, zwany prądem upływowym (ryc. 11.33). Prąd ten można określić za pomocą wzoru Ja=UG, Gdzie G- przewodność izolacji pomiędzy rdzeniem a powłoką kabla. Wcześniej wyprowadzono wzór na pojemność kabla koncentrycznego
Spójrzmy na konkretny przykład. Izolacja kabla koncentrycznego nigdy nie jest idealna. W praktyce ma pewną, choć bardzo niską, przewodność właściwą
. W związku z tym, jeśli do kabla zostanie przyłożone napięcie U, wówczas prąd zacznie zamykać się w izolacji, zwany prądem upływowym (ryc. 11.33). Prąd ten można określić za pomocą wzoru Ja=UG, Gdzie G- przewodność izolacji pomiędzy rdzeniem a powłoką kabla. Wcześniej wyprowadzono wzór na pojemność kabla koncentrycznego 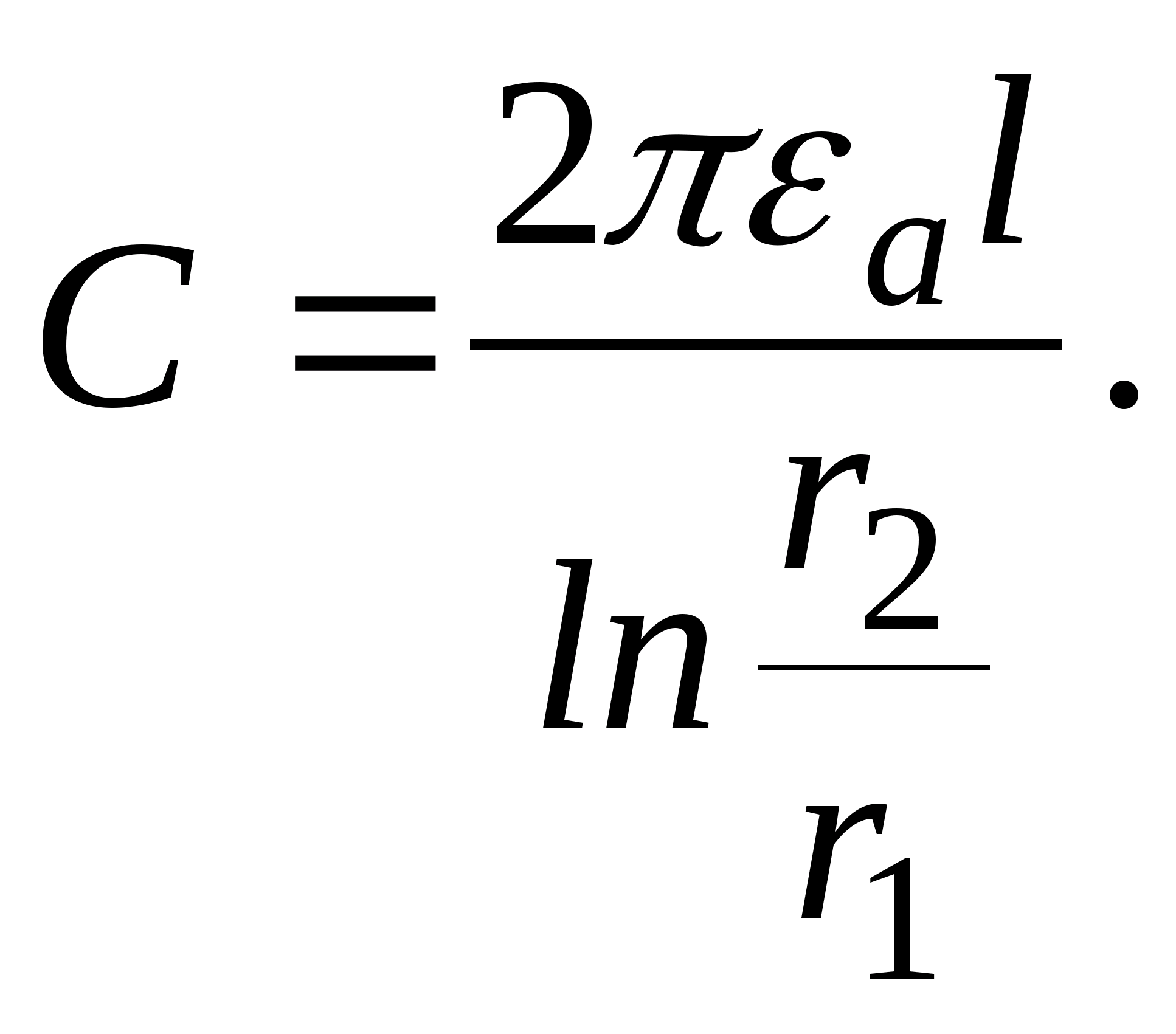 Następnie w oparciu o analogię
Następnie w oparciu o analogię 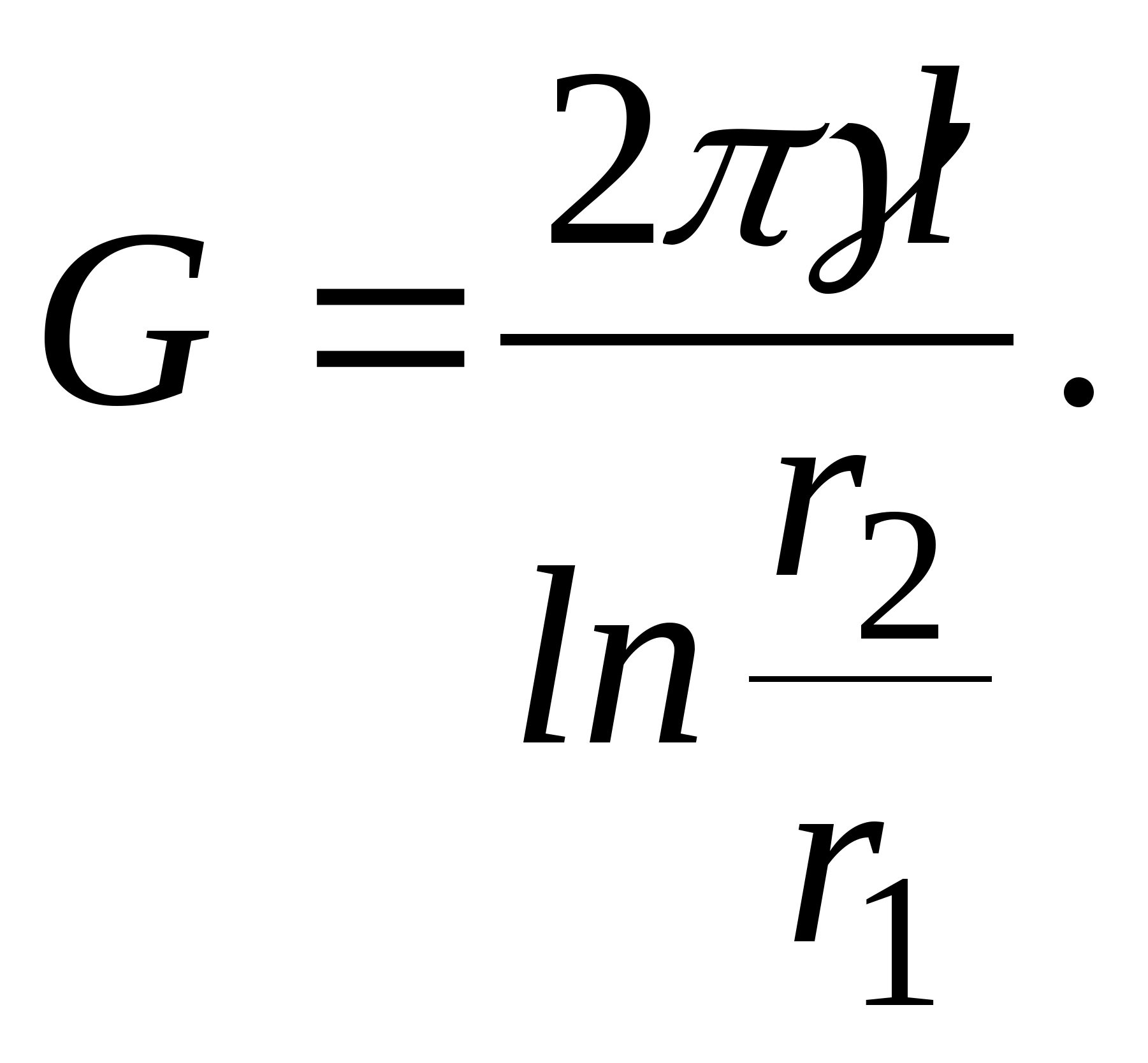
Obliczanie przewodów uziemiających
Aby połączyć dowolne punkty obwodu z ziemią, zakopuje się w nim metalowe przewodniki, do których podłączane są odpowiednie punkty obwodu. Układ takich przewodników zakopanych w ziemi nazywany jest elektrodą uziemiającą. Cel przewodów uziemiających jest zróżnicowany. Są działające uziemienia (tramwaj), są uziemienie ochronne itp. Podczas zwarć (SC) i innych wypadków, a czasem także w trybie normalnym (tramwaj), przez elektrodę masową przepływa prąd, który rozpływa się po ziemi i jednocześnie napotyka na pewien opór, który nazywany jest rezystancją elektroda uziemiająca. Rezystancja uziemienia R H(opór całej ziemi na przepływ prądu) jest jego pierwszą ważną cechą. Drugą ważną cechą jest napięcie krokowe U w– różnica potencjałów pomiędzy dwoma punktami znajdującymi się na powierzchni ziemi, oddalonymi od siebie w odległości kroku człowieka. Ponieważ podczas zwarcia prąd płynący przez elektrodę uziemiającą może przyjmować duże wartości, to wzdłuż powierzchni ziemi może wytworzyć się napięcie krokowe w pobliżu punktu uziemienia, które jest niebezpieczne dla życia ludzkiego. Znanych jest wiele przypadków śmierci ludzi z powodu napięcia krokowego. Stąd znaczenie umiejętności jej obliczenia jest oczywiste. Przy obliczaniu przewodów uziemiających ( R H z opłaty punktowej. Naprężenie w tym miejscu będzie skierowane wzdłuż linii promieniowej (patrz rys. 11.7). Aby to obliczyć, stosujemy wzór. W tym celu przeciągamy przez dany punkt zamkniętą powierzchnię kulistą o środku pokrywającym się z ładunkiem punktowym. Elementarny wektor powierzchniowy U w) przyjęto pewne założenia, z których najważniejsze to:
Lista zadań testowych i problemów zalecanych studentom do przygotowania się do egzaminów z sekcji dyscypliny Fizyka „Elektryczność i magnetyzm” Elementy testowe Pole elektrostatyczne w próżni
DokumentPiłka, jeśli jest jednorodna elektrostatyczny pole kula wydawała się zawieszona w glicerynie. Elektrostatyczny pole skierowany pionowo w górę...
Dielektryki w polu elektrostatycznym. Wektor polaryzacji. Odchylenie elektryczne. Twierdzenie Gaussa dotyczące przemieszczenia elektrycznego. 5
DokumentDipol w elektryce jednorodnej i niejednorodnej pole. 3. Dielektryki w elektrostatyczny pole. Wektor polaryzacji. 4. Elektryczne... 6. Moc elektryczna. Kondensatory. Energia elektrostatyczny pola Przewodniki i dielektryki. Bezpłatne i...
Sprawozdanie z pracy laboratorium nr 1 „Badania pola elektrostatycznego poprzez modelowanie w ośrodku przewodzącym”
RaportPołączenie wyrażone zależnością: (1.1) W dielektrykach elektrostatyczny pole charakteryzujący się wektorem przemieszczenia elektrycznego... wyciągnijmy wniosek o możliwości modelowania elektrostatyczny pola elektryczny pole w środowisku przewodzącym, jeśli zostanie zaobserwowane...
Który rysunek poprawnie przedstawia wzór linii pola elektrostatycznego punktowego ładunku dodatniego?
DokumentNapięcia elektrostatyczny polaładunek Q w punkcie C jest równy EC. Jaki jest moduł napięcia? elektrostatyczny pola... napięcie elektrostatyczny polaładunek Q w punkcie C jest równy EC. Jaki jest moduł napięcia? elektrostatyczny pola ...
Oporność elektrod zakopanych w ziemi nie jest brana pod uwagę.
W ziemi linie prądu nie biegną do nieskończoności, ale gromadzą się na innej elektrodzie. Nie jest to brane pod uwagę, ponieważ ma niewielki wpływ na rozkład prądu w pobliżu danej elektrody, gdzie gęstość prądu jest największa, oraz na wartość odpowiedniej rezystancji uziemienia.
Taka elektroda uziemiająca nie ma napięcia krokowego ze względu na odległe położenie powierzchni ziemi.
Napięcie krokowe gdzie l w to długość kroku osoby, którą zgodnie z Zasadami bezpieczeństwa należy przyjąć jako równą 0,8 M.
Elektroda masowa w kształcie kuli, płytko wkopana w ziemię
mi 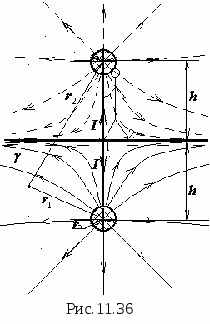 Jeżeli elektroda masowa w kształcie kuli znajduje się blisko powierzchni ziemi (ryc. 11.36), wówczas linie prądu są zniekształcone. Aby uwzględnić ten zniekształcający wpływ powierzchni Ziemi, można zastosować metodę odbicia lustrzanego. Linie prądu w pobliżu powierzchni ziemi muszą być do niej styczne (nie mogą zawierać normalnych składników). Warunek ten zostanie spełniony jeżeli górna półprzestrzeń zostanie mentalnie wypełniona ośrodkiem przewodzącym o tej samej przewodności co ziemia i w tym ośrodku zostanie umieszczona elektroda będąca lustrzanym odbiciem rzeczywistej elektrody względem powierzchni ziemi . Prąd docierający do wyimaginowanej elektrody musi mieć tę samą wartość i znak, co prąd elektrody rzeczywistej. Pole takiego uziomu można wyznaczyć metodą superpozycji z działania rzeczywistego uziomu i jego lustrzanego odbicia. Potencjał dowolnego punktu w polu będzie
Jeżeli elektroda masowa w kształcie kuli znajduje się blisko powierzchni ziemi (ryc. 11.36), wówczas linie prądu są zniekształcone. Aby uwzględnić ten zniekształcający wpływ powierzchni Ziemi, można zastosować metodę odbicia lustrzanego. Linie prądu w pobliżu powierzchni ziemi muszą być do niej styczne (nie mogą zawierać normalnych składników). Warunek ten zostanie spełniony jeżeli górna półprzestrzeń zostanie mentalnie wypełniona ośrodkiem przewodzącym o tej samej przewodności co ziemia i w tym ośrodku zostanie umieszczona elektroda będąca lustrzanym odbiciem rzeczywistej elektrody względem powierzchni ziemi . Prąd docierający do wyimaginowanej elektrody musi mieć tę samą wartość i znak, co prąd elektrody rzeczywistej. Pole takiego uziomu można wyznaczyć metodą superpozycji z działania rzeczywistego uziomu i jego lustrzanego odbicia. Potencjał dowolnego punktu w polu będzie 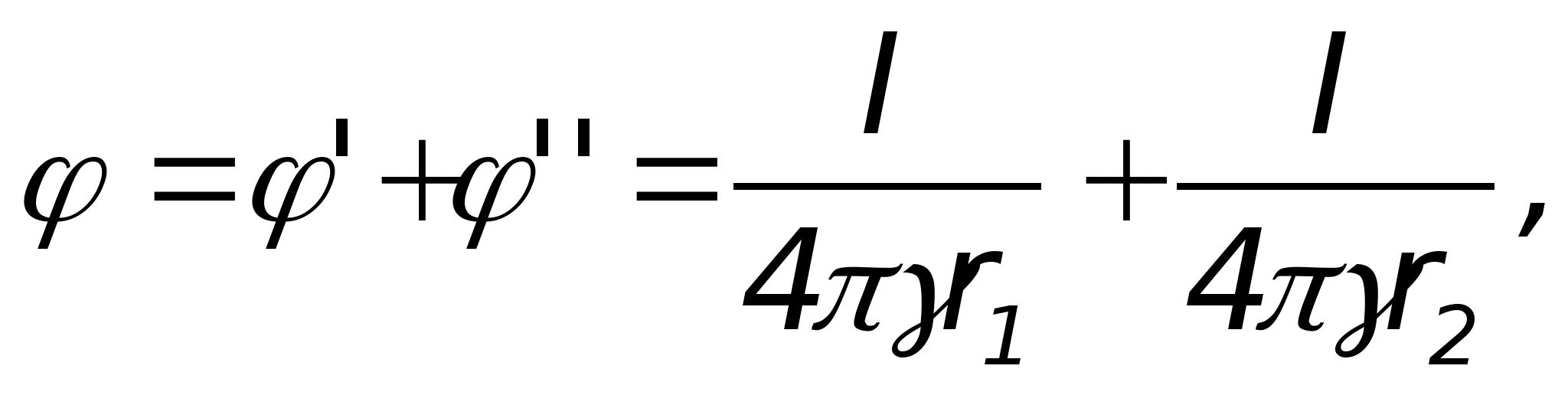 Gdzie pole. Pole Elektrostatyczny pole stworzył... 13 Temat: Elektrostatyczny pole. Pole opłata punktowa. Zasada superpozycji Elektrostatyczny pole utworzony przez punkt dodatni...
Gdzie pole. Pole Elektrostatyczny pole stworzył... 13 Temat: Elektrostatyczny pole. Pole opłata punktowa. Zasada superpozycji Elektrostatyczny pole utworzony przez punkt dodatni...

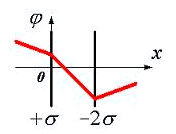
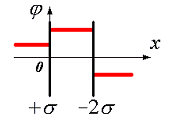
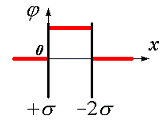
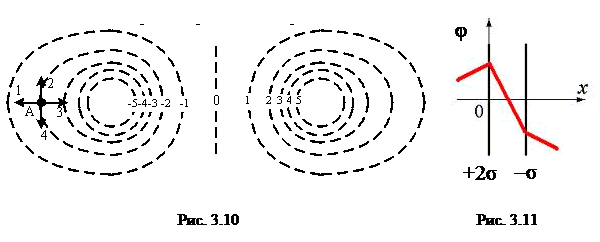
 Ryż. 3.12
Ryż. 3.12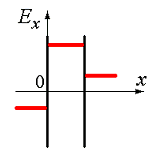 Ryż. 3.13
Ryż. 3.13 Ryż. 3.14
Ryż. 3.14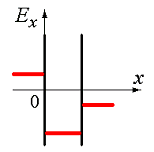 Ryż. 3.15
Ryż. 3.15