Kako riješiti primjere kompleksnih brojeva. Kompleksni brojevi za lutke
IZOLIRANA POSEBNA TOČKA
KOMPLEKSNI BROJEVI I OPERACIJE NAD NJIMA
Čak i najjednostavnije algebarske operacije nad realnim brojevima (vađenje kvadratnog korijena negativnog broja, rješavanje kvadratne jednadžbe s negativnim diskriminantom) vode nas izvan skupa realnih brojeva. Daljnja generalizacija pojma broja dovodi do kompleksnih brojeva. Izvanredno svojstvo skupa kompleksnih brojeva je da je zatvoren u odnosu na osnovne matematičke operacije. Drugim riječima, glavni matematičke operacije nad kompleksnim brojevima ne može se izvesti iz skupa kompleksnih brojeva.
Složeni broj (u algebarskom obliku ) naziva se izraz
gdje su proizvoljni realni brojevi, - imaginarna jedinica , određeno stanjem.
Broj je pozvan pravi dio složeni broj , označen (od latinskog " realis"), poziva se broj imaginarni dio kompleksni broj i označava se (od latinskog " imaginarius»).
Dva kompleksna broja i jednaki su ako i samo ako su im jednaki realni i imaginarni dijelovi: , . Dva kompleksna broja su jednaka ili nisu jednaka (koncepti “više” i “manje” nisu uvedeni za kompleksne brojeve).
Složeni konjugat broj se poziva na broj . Očito je da se kompleksni konjugiran broj podudara s brojem : .
Aritmetičke operacije. Zbrajanje, oduzimanje i množenje složenih brojeva provodi se prema normalna pravila algebra.
Neka , . Zatim
razlika,
raditi,
kvocijent (na )
Primjer 1. Zadani su kompleksni brojevi: , .
Pronaći , , .
Riješenje. ;
Problem 1. Neka i budu par kompleksno konjugiranih brojeva. Pokažite da je njihov zbroj realan broj, razlika imaginaran broj, a njihov umnožak realan nenegativan broj.
Primjer 2. Pronaći , .
Riješenje. ; .
Komentar. Potencije broja mogu se prikazati u obliku tablice
Primjer 3. Množenje brojeva i .
Riješenje.
Primjer 4. Izračunajte a) ; b) ; V) .
Riješenje.
a) Proširimo kvadrat razlike:
b) Proširimo kub zbroja:
Primjer 5. Pronađite kvocijent ako je .
Riješenje.
Primjer 6. Izračunajte a) , b) .
Riješenje. A) .
Prisjetimo se:
Geometrijska interpretacija kompleksnog broja.
Razmotrimo kartezijanski pravokutni koordinatni sustav. Na apscisnu os nanesemo realni dio kompleksnog broja, a na ordinatnu os imaginarni dio. Dobivamo točku s koordinatama . U ovom slučaju svaki kompleksni broj odgovara jednoj točki na ravnini. Vrijedi i obrnuto: svakoj točki na ravnini može se pridružiti kompleksan broj čiji je realni dio jednak apscisi točke, a imaginarni dio jednak ordinati točke. Tako se uspostavlja korespondencija jedan na jedan između kompleksnih brojeva i točaka na ravnini. (Ranije smo govorili o korespondenciji jedan-na-jedan između realnih brojeva i točaka na brojevnom pravcu.)
Zove se ravnina čije točke predstavljaju kompleksne brojeve složena ravnina. Kako bi ga razlikovali od stvarne ravnine s desne strane gornji kut napiši zaokruženo slovo. Os apscisa na takvoj ravnini naziva se realna os, a os ordinata imaginarna os. Kompleksno konjugirani broj je zrcalna slika danog kompleksnog broja oko realne osi. Ishodište koordinata naziva se nulta točka. Udaljenost kompleksnog broja od ishodišta naziva se modul ovaj broj:
Zadatak 2. Dokaži to .
Modul razlike između dva kompleksna broja je udaljenost između odgovarajućih točaka:
Svakoj točki kompleksne ravnine pridružujemo vektor s početkom u nultočki i krajem u ovoj točki. Očito, ovo dopisivanje je jedan na jedan. U ovoj interpretaciji, realni i imaginarni dio kompleksnog broja su prva i druga komponenta vektora. Zbroj je sada predstavljen dijagonalom paralelograma izgrađenog na vektorima i razlika se shvaća kao . Modul kompleksnog broja predstavlja duljinu vektora. Geometrijski očito je nejednakost trokuta u kompleksnoj ravnini: .
Primjer 7. Označite geometrijsko mjesto točaka na kompleksnoj ravnini za koje
| A) ; | b) ; |
| V) ; | G) . |
Riješenje. a) Budući da je , dana dvostruka nejednakost može se prepisati kao: . Dobili smo okomitu prugu.
b) Budući da je , zadanu dvostruku nejednadžbu prepisujemo u obliku: . Dobili smo horizontalnu traku. Samostalno rješavati zadatke c) id).
Primjer 8.
Riješenje. a) Modul kompleksnog broja je duljina vektora koji ide od nul točke do točke, tj. udaljenost od ishodišta do točke. To znači da u ovom slučaju govorimo o geometrijskom položaju točaka u ravnini jednako udaljenih od ishodišta koordinata - to je krug (u ovom slučaju radijus kruga je 1). Problem je bilo moguće prevesti na jezik kartezijevih koordinata:
b) Ovdje govorimo o geometrijskom položaju točaka koje se nalaze izvan kruga radijusa (sa središtem u ishodištu).
c) točke su u prstenu između krugova polumjera i .
Primjer 9. Označite geometrijsko mjesto točaka na kompleksnoj ravnini za koje a) ; b) ; V) .
Riješenje. a) Modul razlike je udaljenost između točke u kompleksnoj ravnini i točke 1. To znači da govorimo o geometrijskom mjestu točaka jednako udaljenih (na udaljenosti 1) od točke 1 - to je kružnica polumjer 1 sa središtem u točki (1;0). U koordiniranom jeziku:
b) Točke se nalaze istovremeno u krugu sa središtem u ishodištu koordinata i u krugu sa središtem pomaknutim u točku: .
c) To su točke desne poluravnine koje leže unutar kružnice: .
Trigonometrijski oblik kompleksnog broja. Argument kompleksni broj je kut koji čini vektor s pozitivnim smjerom realne osi, . Ovaj kut definiran je dvosmisleno:
Ovdje je glavna vrijednost argumenta; ona je istaknuta nejednakostima (tj. na kompleksnoj ravnini napravljen je rez duž realne osi lijevo od ishodišta).
Prvi stupac je označen za broj koji leži na realnoj ili imaginarnoj osi, a drugi stupac je za sve ostale kompleksne brojeve.
Označimo . Budući da je , , tada se može prikazati kompleksan broj u trigonometrijskom obliku :
Dva kompleksna broja i , dana u trigonometrijskom obliku
zbog dvosmislenosti argumenta jednaki su ako i samo ako , .
Primjer 10. Pronađite module i argumente, kao i glavne vrijednosti argumenata kompleksnih brojeva. Svaku od njih napiši u trigonometrijskom obliku.
Riješenje. Moduli svih ovih brojeva su isti:
Argument svakog broja nalazimo uzimajući u obzir četvrtinu u kojoj se nalazi odgovarajuća točka.
1) Poenta je u prvoj četvrtini, što znači
U trigonometrijskom obliku ovdje se uzima u obzir periodičnost kosinusa i sinusa.
2) Poanta je u drugoj četvrtini, što znači
3) Poenta je u trećoj četvrtini, što znači
4) Poanta je u četvrtoj četvrtini, što znači
Množenje i dijeljenje kompleksnih brojeva u trigonometrijskom obliku. Neka su brojevi i dati u trigonometrijskom obliku: , . Pomnožimo ih:
Prisjećajući se formula za kosinus i sinus zbroja dvaju kutova, dobivamo
Vidimo da kada se kompleksni brojevi množe, njihovi se moduli množe i dodaju njihovi argumenti. Geometrijsko značenje ove operacije: predstavljajući brojeve i vektore na kompleksnoj ravnini koja proizlazi iz nulte točke, vidimo da se vektor dobiva iz vektora "istezanjem" za faktor i rotacijom za kut.
Za kvocijent dobivamo formulu:
Primjer 11. Nađi umnožak i kvocijent brojeva
Riješenje. U skladu s formulom (1) pišemo:
Provjerimo rezultat množenjem ovih brojeva u algebarskom obliku:
Pomoću formule (2) nalazimo
U algebarskom obliku ova operacija će biti zapisana na sljedeći način:
Dizanje kompleksnog broja na potenciju. Iz formule (1) slijedi da se podizanje kompleksnog broja na potenciju provodi prema pravilu
Primjer 12. Izračunaj 1) ; 2) .
Riješenje. 1) Gore smo dobili prikaz kompleksnog broja u trigonometrijskom obliku: . Pomoću formule (3) nalazimo . Isti rezultat dobiven je gore u primjeru 4c) korištenjem Newtonovog binoma.
2) Prije svega, predstavimo broj u trigonometrijskom obliku.
točka se nalazi u četvrtoj četvrtini, što znači . Zato
Ostaje koristiti formulu (3):
Proširivanjem kocke razlike dobivamo isti rezultat (provjerite!).
Kada se formula (3) pretvori u Moivreova formula :
Uz njegovu pomoć lako možemo dobiti relacije koje izražavaju sinuse i kosinuse višestrukih kutova s i .
Primjer 13. Ekspresno i kroz i.
Riješenje. Pretpostavljajući Moivreovu formulu, dobivamo:
S lijeve strane proširimo kocku zbroja i sakupimo slične članove:
Ovdje se uzima u obzir da . Došli smo do jednakosti dva kompleksna broja u algebarskom obliku
što je točno ako i samo ako su realni i imaginarni dijelovi tih brojeva jednaki.
Jednakost realnih dijelova daje ;
izjednačavanjem zamišljenih dijelova dobivamo .
Vađenje korijena kompleksnog broja. Ako su kompleksni brojevi povezani relacijom, onda je . Predstavimo brojeve u trigonometrijskom obliku:
Naš zadatak je odrediti (tj. i ) iz zadanog broja (tj. iz poznatih i ). U skladu s formulom (3) jednakost će biti zapisana u obliku
Iz jednakosti dva kompleksna broja u trigonometrijskom obliku slijedi:
Ovdje je th korijen realnog nenegativnog broja. To znači da za th korijen kompleksnog broja dobivamo formulu
Pretpostavljajući sekvencijalno, dobivamo različite vrijednosti:
Svi ti korijeni imaju iste module, tj. odgovarajuće točke nalaze se na kružnici radijusa sa središtem u ishodištu. Argumenti dvaju susjednih korijena razlikuju se za kut. To znači da se sve vrijednosti korijena th kompleksnog broja nalaze u vrhovima pravilnog kuta upisanog u krug polumjera .
Primjer 14. Pronađite sve vrijednosti th korijena kompleksnog broja i nacrtajte ih na kompleksnoj ravnini if. Imajte na umu da i na. . Dobili smo dva kompleksna konjugirana korijena.
Primjeri rješavanja složenih brojeva navedeni su na kraju članka, ali za sada shvatimo što su složeni brojevi.
U matematici, osim prirodnih, racionalnih i realnih brojeva, postoji još jedna vrsta tzv kompleksni brojevi. Takav skup obično se označava simbolom.
Pogledajmo što je kompleksan broj. Zapišimo to ovako: , u kojoj je zamišljena jedinica , brojevi su stvarni.
Ako ga stavite, tada se složeni broj pretvara u pravi broj. Dakle, možemo zaključiti da su realni brojevi poseban slučaj složen i zapiši ga kao podskup. Usput, također je moguće da.
Uobičajeno je da se imaginarni dio kompleksnog broja piše kao, a kao realni dio.
Uvedimo pojam kompleksno konjugiranih brojeva. Za svaki kompleksni broj postoji takav koji se naziva njegovim konjugatom. Takvi se brojevi međusobno razlikuju samo u predznacima između realnog i imaginarnog dijela.
Kompleksni oblik broja
U matematici se događa da ti brojevi imaju nekoliko oblika. Broj je isti, ali se može pisati drugačije:
- Algebarski
- Indikativno
- Trigonometrijski
Slika kompleksnih brojeva
Gornju smo studiju započeli s algebarskim oblikom. Jer je temeljna. Da budemo jasniji, prikažimo složeni broj na ravnini u istom obliku:
Vidimo da se nalaze na odgovarajućim osima ravnine.
Kompleksni broj je predstavljen kao vektor.
Argument je označen.
Modul je jednak duljini vektora i nalazi se formulom
Argument kompleksnog broja mora se pronaći pomoću različitih formula ovisno o poluravnini u kojoj se sam broj nalazi.
Operacije nad kompleksnim brojevima
Na kompleksnim brojevima mogu se izvoditi različite operacije, i to:
- Zbrajati i oduzimati
- Pomnožite i podijelite
- Izvadite korijene i podignite na snagu
- Prijenos iz jednog oblika u drugi
Za pronalaženje zbroja i razlike Zbrajaju se i oduzimaju samo pojmovi koji međusobno odgovaraju. Imaginarni dio je samo sa imaginarnim, a stvarni dio je samo sa stvarnim:
Množenje u algebarskom obliku:
Množenje u eksponencijalnom obliku:
Dijeljenje u algebarskom obliku:
Dijeljenje u eksponencijalnom obliku:
Za potenciranje trebate pomnožiti složeni broj samim sobom potreban iznos puta ili upotrijebite Moivreovu formulu:
Za vađenje korijena Također morate koristiti Moivreovu formulu:
Teorija kompleksnih brojeva također pomaže u pronalaženju korijena polinoma. Na primjer, u kvadratna jednadžba, ako, tada nema pravih korijena, ali ima složenih korijena. Posljednji primjer ispituje ovaj slučaj.
Razmotrimo kompleksne brojeve u praksi: primjeri s rješenjima.
Primjeri s rješenjem
| Primjer 4 |
| Dignite kompleksni broj na potenciju: a) b) |
| Riješenje |
|
Da biste ga kvadrirali, samo pomnožite broj samim sobom: Koristimo formulu za množenje, otvaramo zagrade i dajemo slične: Dobili smo odgovor da U ovom slučaju nije sve tako jednostavno kao u prethodnom slučaju, kada je došlo do kvadrature. Naravno, možete pribjeći prethodno spomenutoj metodi i pomnožiti broj sam sa sobom 7 puta, ali to će biti vrlo dugo i dugotrajno rješenje. Bit će puno lakše koristiti se Moivreovom formulom. Ali radi s brojevima u trigonometrijskom obliku, a broj je dan u algebarskom obliku. To znači da ćemo prvo prijeći iz jednog oblika u drugi. Izračunavamo vrijednost modula: Pronađimo koji je argument: Zapisujemo ga u trigonometrijskom obliku: Podignite na potenciju: Pretvorimo ga u algebarski oblik radi jasnoće: |
| Odgovor |
U članku " Kompleksni brojevi: primjeri s rješenjima" data je definicija, osnovni pojmovi, notni oblici, algebarske operacije i rješenja praktičnih primjera.
Upoznat ćemo se s pojmom kompleksnog broja, razmotriti algebarski, trigonometrijski i eksponencijalni oblik kompleksnog broja. Također ćemo naučiti kako izvoditi operacije s kompleksnim brojevima: zbrajanje, oduzimanje, množenje, dijeljenje, stepenovanje i vađenje korijena. Ne brini, uplašio sam te, nasmijat ću te. Za svladavanje složenih brojeva dovoljno je znati izvoditi osnovne algebarske operacije s “običnim” brojevima, te malo poznavati trigonometriju.
1) Pojam kompleksnog broja. 2) Algebarski oblik kompleksnog broja. Zbrajanje, oduzimanje, množenje i dijeljenje kompleksnih brojeva. 3) Trigonometrijski i eksponencijalni oblik kompleksnog broja. 4) Dizanje kompleksnih brojeva na potencije. 5) Vađenje korijena iz kompleksnih brojeva. Kvadratna jednadžba s kompleksnim korijenima.
Prvo, prisjetimo se “običnih” školskih brojeva. U matematici se nazivaju skup realnih brojeva i označavaju se slovom (u literaturi i rukopisima veliko slovo “er” piše se podebljano ili debelo). Svi realni brojevi prikazani su na brojevnom pravcu:

Društvo realnih brojeva vrlo je raznoliko - ovdje postoje cijeli brojevi, razlomci i iracionalni brojevi. U tom slučaju svaka brojčana točka nužno odgovara nekom realnom broju.
Pojam kompleksnog broja
Prije nego što prijeđemo na složene brojeve, dat ću važan savjet: Ne pokušavajte predstaviti složeni broj "u životu" - to je kao da pokušavate prikazati četvrtu dimenziju u našem trodimenzionalnom prostoru. Ako želite, složeni broj je dvodimenzionalni broj.
Kompleksni broj je broj oblika , gdje su i realni brojevi, tzv imaginarna jedinica. Broj je pozvan pravi dio ( ) složeni broj, broj se zove imaginarni dio ( ) složeni broj.
– ovo je JEDAN BROJ, a ne zbrajanje. Realni i imaginarni dijelovi kompleksnog broja, u načelu, mogu se preurediti: ili se imaginarna jedinica može preurediti: – to neće promijeniti kompleksni broj. Ali uobičajeno je pisati složeni broj ovim redoslijedom::
Da bi sve bilo jasnije, odmah ćemo dati geometrijsku interpretaciju. Kompleksni brojevi su predstavljeni sa složena ravnina:
 Kao što je gore spomenuto, slovo obično označava skup realnih brojeva. Gomila isti kompleksni brojevi obično se označava "podebljanim" ili podebljanim slovom. Dakle, slovo treba staviti na crtež, ukazujući na činjenicu da imamo složenu ravninu.
Kao što je gore spomenuto, slovo obično označava skup realnih brojeva. Gomila isti kompleksni brojevi obično se označava "podebljanim" ili podebljanim slovom. Dakle, slovo treba staviti na crtež, ukazujući na činjenicu da imamo složenu ravninu.
Kompleksna ravnina sastoji se od dvije osi: – realne osi, – imaginarne osi
Pravila za oblikovanje crteža gotovo su ista kao i za crtež u kartezijanskom sustavu. Duž osi trebate postaviti dimenziju, označiti: nula; jedinica duž realne osi; imaginarna jedinica duž imaginarne osi.
Konstruirajmo sljedeće kompleksne brojeve na kompleksnoj ravnini (vidi stranicu 3):
Po kojem se principu označavaju brojevi na kompleksnoj ravnini, mislim da je očito - kompleksni brojevi označavaju se na isti način kao što smo označavali točke u 5.-6. razredu na nastavi geometrije.
Razmotrimo sljedeće kompleksne brojeve: , , . Reći ćete, to su obični realni brojevi! I bit ćete gotovo u pravu. Realni brojevi su poseban slučaj kompleksnih brojeva. Realna os označava upravo skup realnih brojeva, odnosno svi naši “obični” brojevi sjede na osi. Izjava se može strože formulirati na sljedeći način: Skup realnih brojeva je podskup skupa kompleksnih brojeva.
Brojevi , , su kompleksni brojevi s nultim imaginarnim dijelom. Brojevi , , su, naprotiv, čisto imaginarni brojevi, tj. brojevi s nultim realnim dijelom. Nalaze se strogo na imaginarnoj osi.
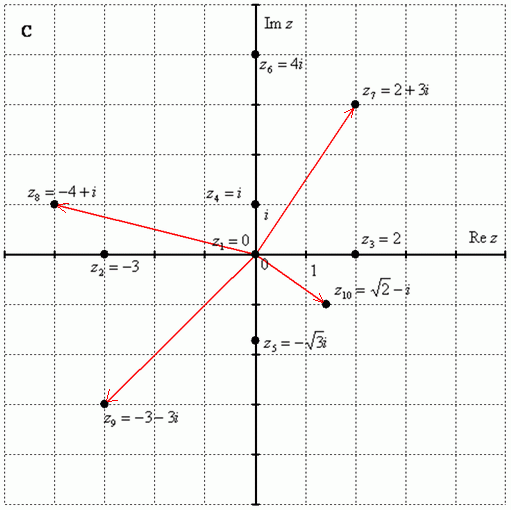
U brojevima , , , ni realni ni imaginarni dio nisu jednaki nuli. Takvi se brojevi također označavaju točkama na kompleksnoj ravnini, a uobičajeno je da im se radijus vektori povlače iz ishodišta koordinata (na crtežu označeno crvenom bojom). Radijus vektori na brojeve koji se nalaze na osi obično se ne crtaju, jer se spajaju s osima.
