Volumetrijska gustoća energije elektrostatičkog polja lopte

(Primjeri rješavanja problema)

Energija međudjelovanja naboja

Primjer 1.

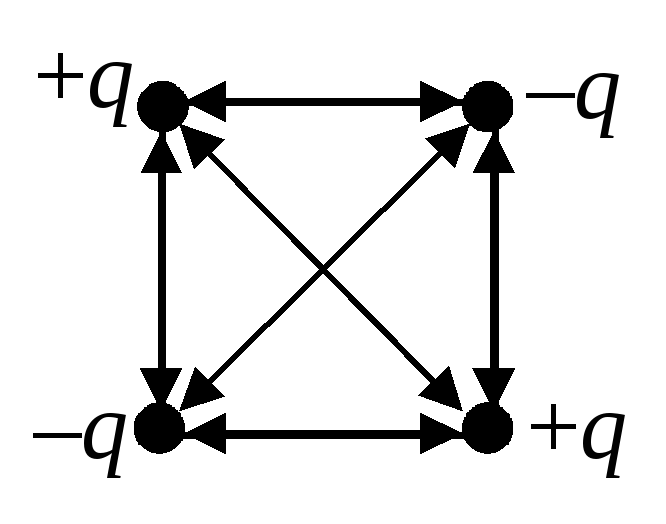
Odredite električnu energiju međudjelovanja točkastih naboja koji se nalaze na vrhovima kvadrata sa stranicom a(vidi sliku 2).

Riješenje.

Na slici 3 sve parne interakcije naboja konvencionalno su prikazane dvosmjernim strelicama. Uzimajući u obzir energije svih ovih interakcija, dobivamo:

Primjer 2.

Odredite električnu energiju interakcije nabijenog prstena s dipolom koji se nalazi na njegovoj osi, kao što je prikazano na slici 4. Poznate udaljenosti a, l, naknade Q, q i radijus prstena R.

Riješenje.

Pri rješavanju problema treba uzeti u obzir sve energije parnih interakcija naboja jednog tijela (prstena) s nabojima drugog tijela (dipola). Energija interakcije točkasti naboj q s naplatom Q raspoređena po prstenu određena je zbrojem

Gdje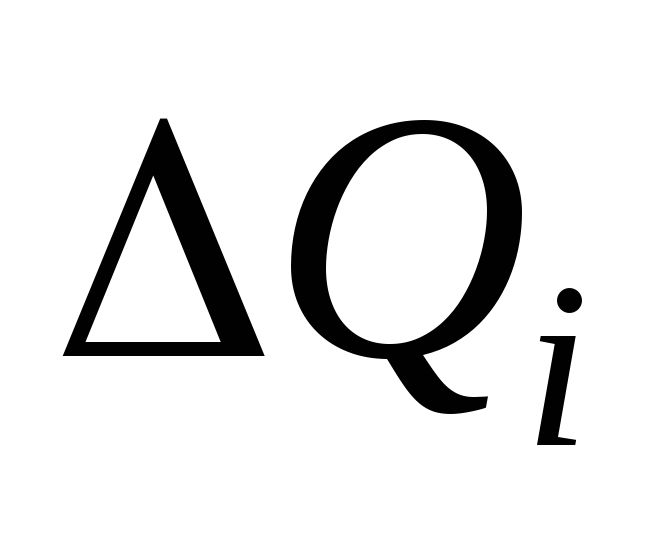

- naboj infinitezimalnog fragmenta prstena, - udaljenost od ovog fragmenta do naboja q. Jer sve isti i jednaki

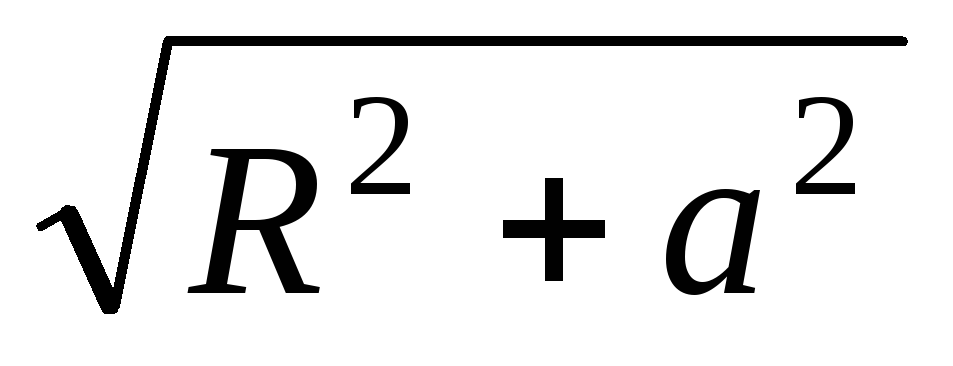, To

Slično, nalazimo energiju interakcije točkastog naboja – q s nabijenim prstenom:

Sažimajući W 1 i W 2, dobivamo za energiju interakcije prstena s dipolom:

Električna energija nabijenih vodiča

Primjer 3.

Definirajte posao električne sile kada se radijus jednoliko nabijene kugle smanji za faktor 2. Sferni naboj q, njegov početni radijus R.

Riješenje.

Električna energija usamljenog vodiča određena je formulom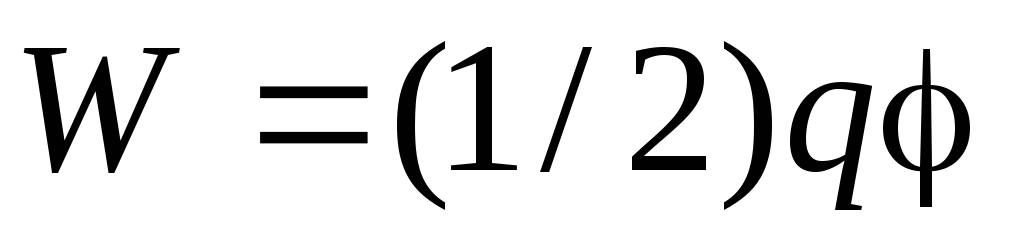

, Gdje q– naboj vodiča,  – njegov potencijal. Uzimajući u obzir da potencijal jednoliko nabijene kugle polumjera R jednaki

, nađimo njegovu električnu energiju:

Nakon što se polumjer kugle prepolovi, njezina energija postaje jednaka

Električne sile djeluju

Primjer 4.

Dvije metalne kuglice čiji su polumjeri r i 2 r, a odgovarajući naboji su 2 q i - q, smještene u vakuumu na velikoj udaljenosti jedna od druge. Koliko puta će se smanjiti Električna energija sustav ako su kuglice spojene tankom žicom?

Riješenje.

Nakon spajanja kuglica tankom žicom njihovi potencijali postaju isti

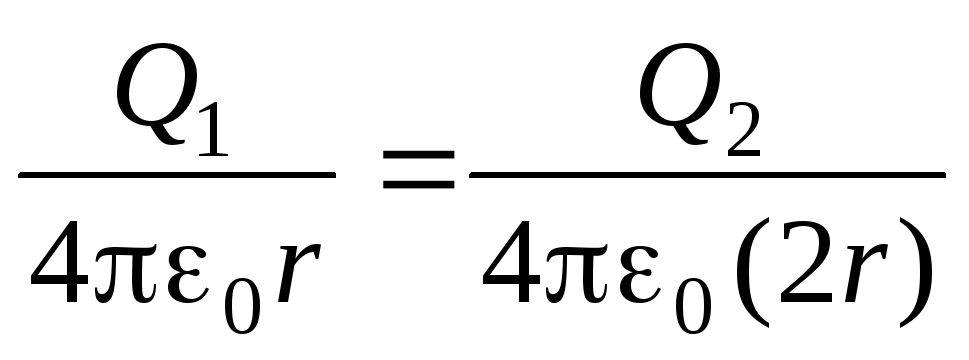i postojani naboji kuglica Q 1 i Q 2 dobivaju se kao rezultat protoka naboja s jedne kuglice na drugu. U tom slučaju ukupni naboj kuglica ostaje konstantan:

Iz ovih jednadžbi nalazimo

,

.

Energija kuglica prije nego što su spojene žicom jednaka je

a nakon spajanja

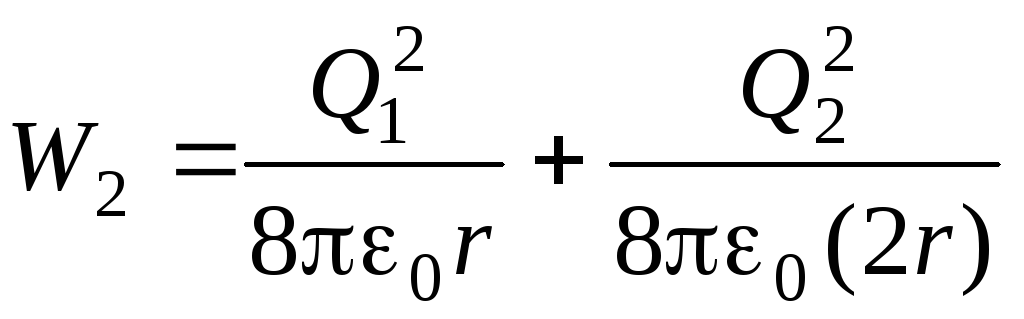Zamjena vrijednosti u posljednji izraz Q 1 i Q 2, dobivamo nakon jednostavnih transformacija

Primjer 5.

Spojeni u jednu kuglu N= 8 identičnih živinih kuglica od kojih svaka ima naboj q. Uz pretpostavku da su u početnom stanju živine kuglice bile na velikoj udaljenosti jedna od druge, odredite koliko se puta povećala električna energija sustava.

Riješenje.

Kada se živine sfere spoje, njihov ukupni naboj i volumen ostaju sačuvani:

Gdje Q– naboj lopte, R– njegov radijus, r je polumjer svake male živine kuglice. Ukupna električna energija N samotne lopte je jednako

Električna energija nastale lopte

Nakon algebarskih transformacija dobivamo

= 4.

Primjer 6.

Metalna polumjerna kugla R= 1 mm i naboj q= 0,1 nC S velika udaljenost polako prilazi nenabijenom vodiču i zaustavlja se kada potencijal kuglice postane jednak  = 450 V. Koliki rad za to treba izvršiti?

Riješenje.

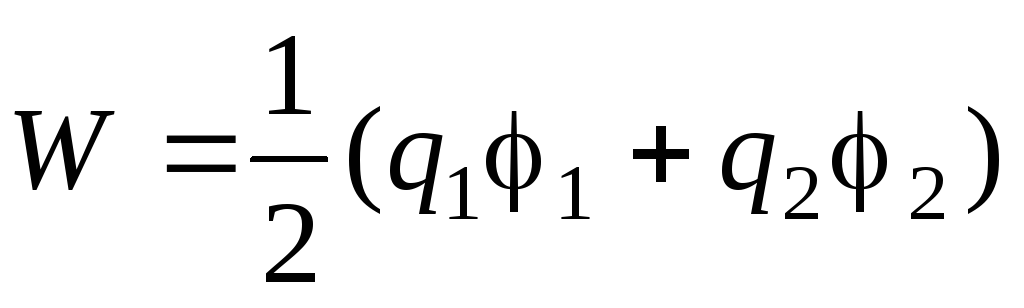Gdje q 1 i q 2 – naboji vodiča,  1 i  2 – njihovi potencijali. Budući da vodič prema problemu nije nabijen, onda

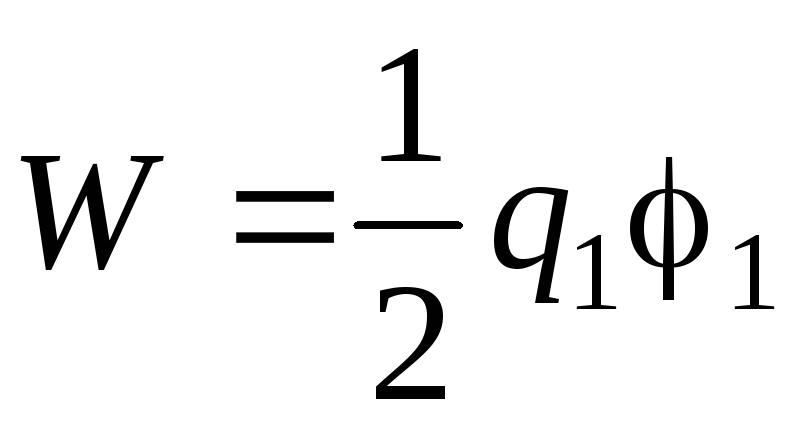Gdje q 1 i 1 naboj i potencijal kuglice. Kada su kuglica i nenabijeni vodič na velikoj udaljenosti jedan od drugog,

i električne energije sustava

U konačnom stanju sustava, kada potencijal kuglice postane jednak , električna energija sustava je:

Rad vanjskih sila jednak je prirastu električne energije:

= –0,0225 µJ.

primijeti da električno polje u konačnom stanju sustava stvaraju naboji inducirani na vodiču, kao i naboji nejednoliko raspoređeni po površini metalne kuglice. Vrlo je teško izračunati ovo polje s poznatom geometrijom vodiča i zadanim položajem metalne kuglice. Nismo to morali raditi jer problem ne specificira geometrijsku konfiguraciju sustava, već potencijal lopte u konačnom stanju.

Primjer 7 .

Sustav se sastoji od dvije koncentrične tanke metalne ljuske polumjera R 1 i R 2 (

i pripadajuće naknade q 1 i q 2. Pronađite električnu energiju W sustava. Razmotrite i poseban slučaj kada

.

Riješenje.

Električna energija sustava od dva nabijena vodiča određena je formulom

Za rješavanje problema potrebno je pronaći potencijale unutarnje ( 1) i vanjske ( 2) sfere. To nije teško učiniti (pogledajte odgovarajući odjeljak priručnika):

,

.

Zamjenom ovih izraza u formulu za energiju, dobivamo

Na

energija je jednaka

Vlastita električna energija i energija interakcije

Primjer 8.

Dvije provodne kuglice čiji naboji q i - q, polumjeri R 1 i R 2 nalaze se u vakuumu na velikoj udaljenosti jedna od druge. Kugla većeg radijusa R 2 sastoji se od dvije hemisfere. Hemisfere su odvojene, dovedene u sferu radijusa R 1 i ponovno su spojeni, tvoreći tako kuglasti kondenzator. Odredite rad električnih sila kod ove konstrukcije kondenzatora.

Riješenje.

Električna energija dviju nabijenih kuglica udaljenih jedna od druge jednaka je

Električna energija rezultirajućeg sferičnog kondenzatora:

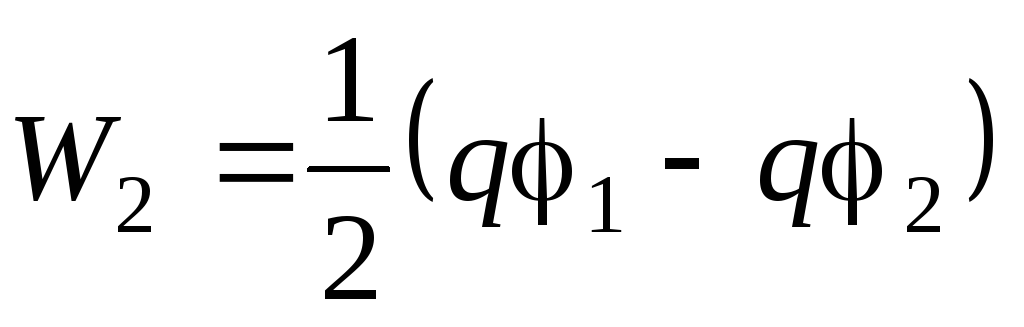Potencijal unutarnje sfere,

- potencijal vanjske sfere. Stoga,

Rad električnih sila s ovim dizajnom kondenzatora:

Imajte na umu da električna energija sfernog kondenzatora W 2 jednak je radu vanjskih sila za punjenje kondenzatora. U ovom slučaju električne sile rade

. Ovaj rad se ne vrši samo kada se nabijene ploče približe jedna drugoj, već i kada se naboj primijeni na svaku od ploča. Zato A EL se razlikuje od gore navedenog rada A, usavršen električnim silama tek kad se ploče spoje.

Primjer 9.

Točkasti naboj q= 1,5 µC nalazi se u središtu kuglaste ljuske po čijoj je površini naboj ravnomjerno raspoređen Q= 5 µC. Nađite rad električnih sila kada se ljuska širi - njezin radijus se povećava od R 1 = 50 mm do R 2 = 100 mm.

Riješenje.

Energija međudjelovanja točkastog naboja q s nabojima koji se nalaze na sfernoj ljusci radijusa R jednak

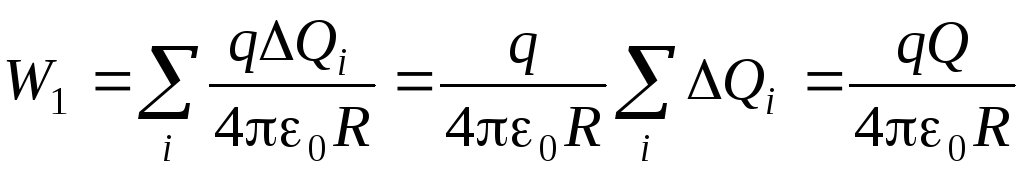Vlastita električna energija ljuske (energija međusobnog djelovanja naboja ljuske) jednaka je:

Rad električnih sila pri širenju ljuske:

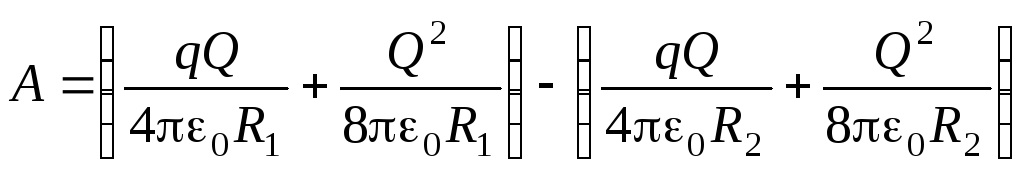Nakon transformacija dobivamo

1,8 J.

Još jedno rješenje

Zamislimo točkasti naboj u obliku jednoliko nabijene kugle malog radijusa r i naplatiti q. Ukupna električna energija sustava jednaka je

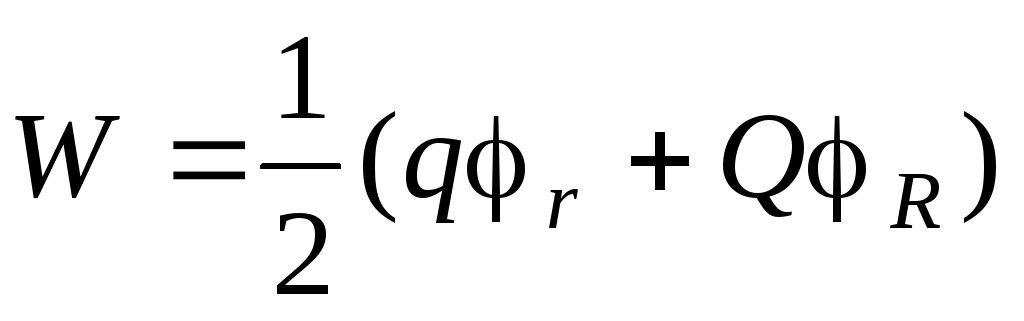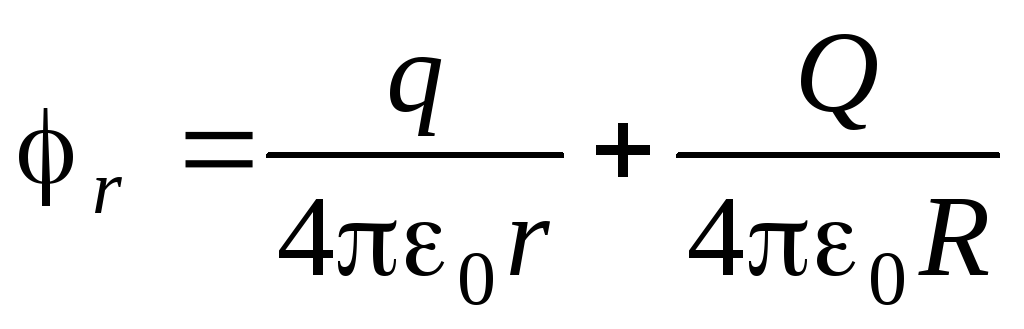
Potencijal polumjerne sfere r,

Potencijal polumjerne sfere R. Kada se vanjska sfera širi, električne sile rade

Nakon zamjena i transformacija dobivamo odgovor.

Volumetrijska gustoća energije električnog polja

Primjer 10 .

Koji je dio električne energije nabijene vodljive kuglice koja se nalazi u vakuumu sadržan u zamišljenoj kugli koncentričnoj s kuglicom, polumjera koje je n puta radijus lopte?

Riješenje.

Volumetrijska gustoća energije električnog polja

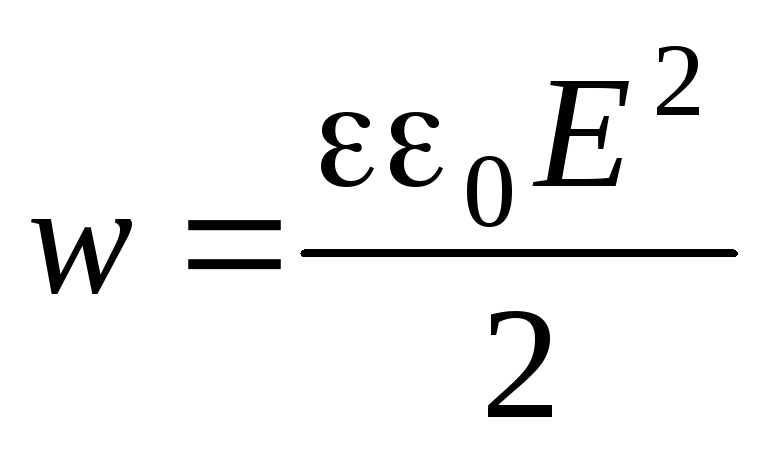
definira električnu energiju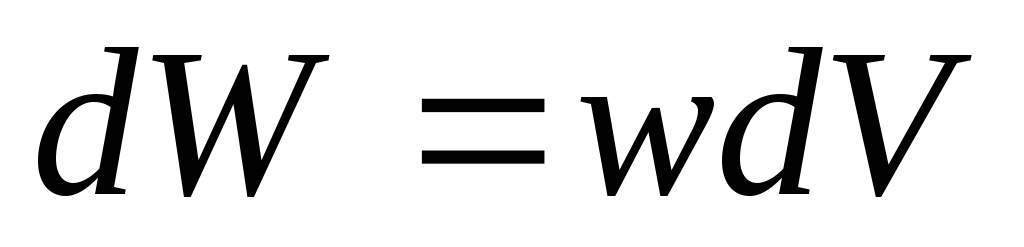

, lokaliziran u infinitezimalnom volumenu

(E– modul vektora jakosti električnog polja u ovom volumenu,  – dielektrična konstanta). Da bismo izračunali ukupnu električnu energiju nabijene vodljive kuglice, mentalno podijelimo sav prostor u beskonačno tanke sferne slojeve koncentrične s nabijenom kuglicom. Razmotrimo jedan od ovih slojeva radijusa r i debljine dr(vidi sliku 5). Njegov volumen je

i električna energija koncentrirana u sloju

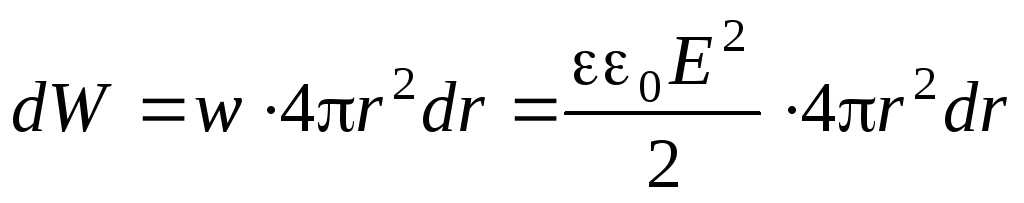Napetost E polje nabijene vodljive kuglice ovisi, kao što je poznato, o udaljenosti r u središte lopte. Unutar lopte

, stoga je pri proračunu energije dovoljno uzeti u obzir samo one sferne slojeve čiji radijus r koji prelazi radijus lopte R.

Na

jakost polja

dielektrična konstanta

i stoga

Gdje q– naboj lopte.

Ukupna električna energija nabijene kuglice određena je integralom

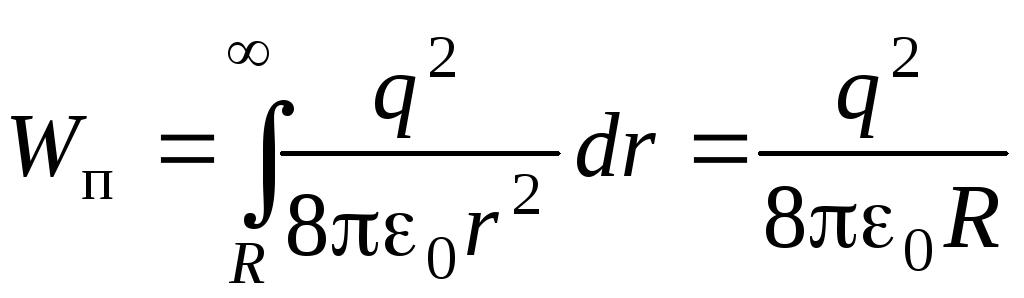a energija koncentrirana unutar zamišljene sfere radijusa nR, je jednako

Stoga,

Primjer 11.

Odredite električnu energiju sustava koji se sastoji od nabijene vodljive kuglice i nenabijenog vodljivog sferičnog sloja koncentričnog s njom (slika 6). Unutarnji i vanjski radijus sloja a I b, radijus lopte

, naplatiti q, sustav je u vakuumu.

Riješenje.

S unutarnje strane i vanjske površine inducirani naboji raspoređeni su u sfernom sloju. Njihov algebarski zbroj je nula, pa inducirani naboji ne stvaraju električno polje na

, Gdje r– udaljenost od središta sustava. U području

jakost polja induciranih naboja također je jednaka nuli, budući da su jednoliko raspoređeni po sfernim površinama. Dakle, električno polje sustava koincidira s poljem sfere jednoliko nabijene po površini, s izuzetkom unutarnjeg područja sferičnog sloja, gdje E= 0. Na slici 7 prikazan je približan graf ovisnosti

. Izostavljajući detaljne proračune (vidi primjer 10), za električnu energiju sustava pišemo:

Gdje

,

,

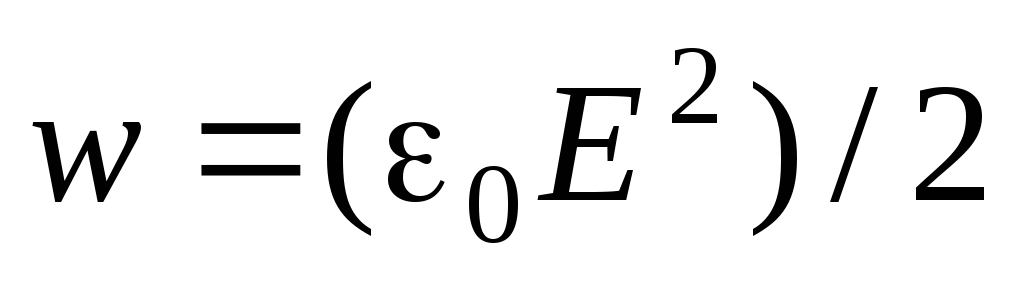. Nakon integracije dobivamo

Primjer 12.

Početno punjenje q ravnomjerno raspoređena po volumenu lopte radijusa R. Zatim se zbog međusobnog odbijanja naboji pomaknu na površinu kuglice. Koliki rad vrše električne sile? Smatrajte da je dielektrična konstanta jednaka jedinici.

Riješenje.

Rad električnih sila jednak je gubitku električne energije:

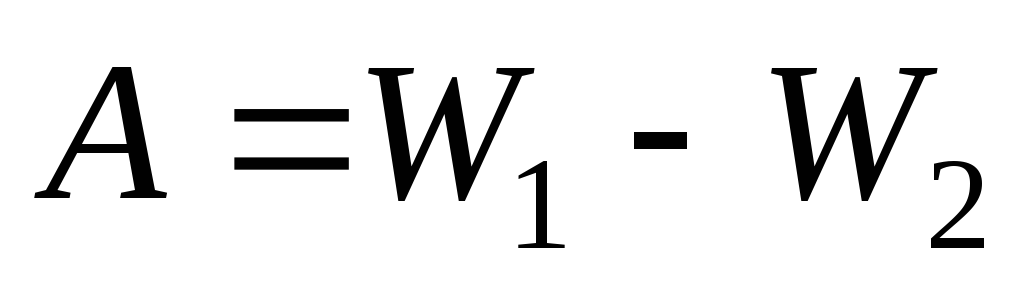Gdje W 1 – električna energija kugle jednoliko nabijene po volumenu, W 2 – energija iste kuglice, jednoliko nabijene po površini. Budući da je ukupni naboj u oba slučaja isti, električno polje izvan kuglice se ne mijenja kada naboj prijeđe iz volumena na površinu. Električno polje i energija mijenjaju se samo unutar lopte.

Koristeći Gaussov teorem, možemo izvesti formulu za jakost polja unutar jednoliko nabijene lopte na udaljenosti r iz njegovog središta:

Električna energija koncentrirana unutar lopte određena je integralom:

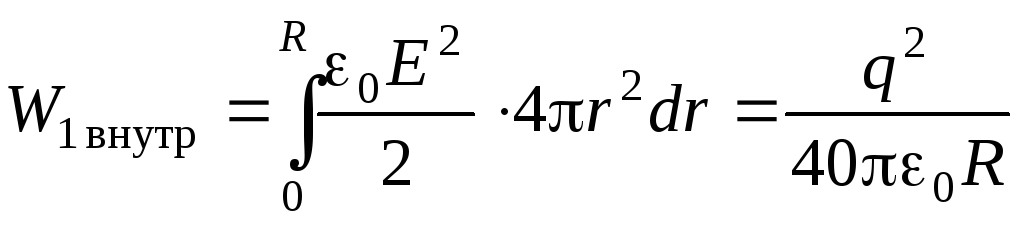Kad su svi naboji prešli na površinu kuglice, električno polje, a time i energija električnog polja unutar kuglice, postalo je nula. Tako,

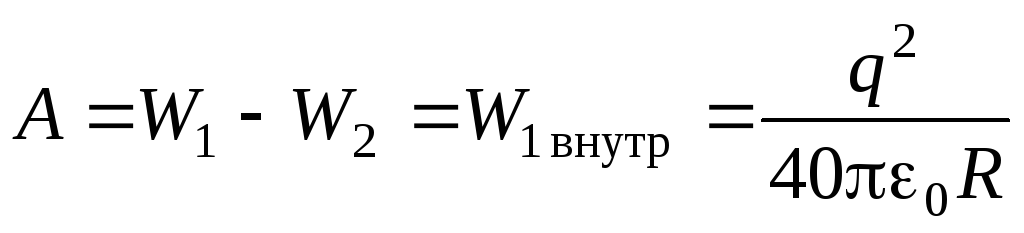Jedno od najzanimljivijih i najkorisnijih otkrića u mehanici je zakon održanja energije. Poznavajući formule za kinetičku i potencijalnu energiju mehaničkog sustava, u mogućnosti smo otkriti vezu između stanja sustava u dva različita vremenska trenutka, bez ulaženja u detalje onoga što se događa između tih trenutaka. Sada želimo odrediti energiju elektrostatičkih sustava. U elektricitetu će se očuvanje energije pokazati jednako korisnim u otkrivanju mnogih zanimljivih činjenica.

Zakon prema kojem se mijenja energija tijekom elektrostatske interakcije vrlo je jednostavan; zapravo, već smo razgovarali o tome. Neka postoje naboji i razdvojeni prazninom. Ovaj sustav ima nešto energije jer je bilo potrebno malo rada da se naboji spoje. Izračunali smo rad kada se dva naboja približe jedan drugome na veliku udaljenost; jednako je

Iz principa superpozicije znamo da ako postoji mnogo naboja, tada je ukupna sila koja djeluje na bilo koji od naboja jednaka zbroju sila koje djeluju na dio svih ostalih naboja. Iz toga slijedi da je ukupna energija sustava od nekoliko naboja zbroj članova koji izražavaju međudjelovanje svakog para naboja zasebno. Ako su i neka dva naboja i udaljenost između njih (sl. 8.1), tada je energija ovog para jednaka

Slika 8.1. Elektrostatska energija sustava čestica je zbroj elektrostatičke energije svaki par

Ukupna elektrostatička energija je zbroj energija svih mogućih parova naboja:

(8.3)

Ako je distribucija dana gustoćom naboja, tada se zbroj u (8.3) mora, naravno, zamijeniti integralom.

O energiji ćemo ovdje govoriti iz dvije perspektive. Prvi je primjena koncepta energije na elektrostatičke probleme; drugi - različiti putevi energetske procjene. Ponekad je lakše izračunati izvršeni rad u nekom slučaju nego procijeniti vrijednost zbroja u (8.3) ili vrijednost odgovarajućeg integrala. Za uzorak izračunavamo energiju potrebnu da se od naboja sastavi jednoliko nabijena kuglica. Energija ovdje nije ništa drugo nego rad koji se troši na prikupljanje naboja iz beskonačnosti.

Zamislite da gradimo loptu tako što sferne slojeve infinitezimalne debljine uzastopno slažemo jedan na drugi. U svakoj fazi procesa skupljamo malu količinu elektriciteta i stavljamo je u tanki sloj od do . Nastavljamo s ovim procesom sve dok ne postignemo zadani radijus (slika 8.2). Ako je naboj na kuglici u trenutku kada je kuglica dovedena do polumjera , tada je rad potreban da se kuglici preda naboj jednak

Slika 8.2. Energija jednoliko nabijene lopte može se izračunati tako da se zamisli da je oblikovana uzastopnim nalaganjem kuglastih slojeva jedan na drugi.

Ako je gustoća naboja unutar kuglice , tada je naboj jednak

a naboj je jednak na svim parovima točaka unutar lopte.

Neka električno punjenje Q ravnomjerno raspoređene po površini kugle radijusa R. Izvan kugle, električno polje koje stvaraju naboji na kugli ekvivalentno je polju točkastog naboja smještenog u središtu kugle (sl. 350).

riža. 350
Unutar sfere nema polja. Dakle, jakost polja u točki koja se nalazi na udaljenosti r iz središta sfere jednako je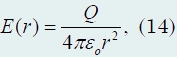

posebno, izravno na površini kugle, jakost polja je
(15)
Imajte na umu da rad S = 4πR 2 je površina sfere, zatim omjer

je površinska gustoća naboja na sferi, tako da se jakost polja na površini sfere izražava istom formulom kao i jakost polja između ploča o kojoj se raspravljalo u prethodnom odjeljku E o = σ/ε o. Površinski potencijal sfere smo također ranije izračunali

Izračunajmo sada energiju polja koju stvaraju naboji na kugli. Mentalno podijelite naboj sfere na N jednaki mali dijelovi čije su veličine jednake

Razmotrimo jedan od ovih malih naboja. Na mjestu gdje se nalazi, potencijal polja stvoren od strane svih ostalih (N − 1) naknade jednake su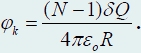

Korištenje simetrične formule

izraz za energiju interakcije poprima oblik

ovaj iznos sadrži N identični pojmovi, dakle jednaki

Budući da je broj dijelova N, u koje je kugla razdijeljena, može se učiniti proizvoljno velikim, tada u granici N → ∞ termin 1/N nestaje, stoga konačni izraz za energiju međudjelovanja naboja kugle ima oblik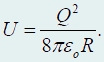

Imajte na umu da dobiveni izraz ima oblik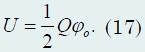

Ako odmah navedemo da smanjenje naboja za mala količina δQ zanemarivo mijenja potencijal sfere, tada se rezultat (17) dobiva izravnom primjenom formule za energiju međudjelovanja naboja. No, rukovanje malim količinama zahtijeva određenu rigoroznost, zbog čega smo dali nešto “oduljeni” zaključak.
Navedimo još jedan zaključak iz istog Formula 1. Da bismo to učinili, izračunavamo energiju sustava kao rad koji se mora obaviti da se kugla napuni. Mentalno ćemo nabiti kuglu malim jednakim dijelovima naboja

koju ćemo prenijeti na sferu iz “beskonačnosti”. Ako kugla nije nabijena, prijenos prvog "dijela" naboja ne zahtijeva nikakav rad. Nakon što je kugla stekla određeni električni naboj, prijenos sljedećeg dijela naboja zahtijeva rad na prevladavanju odbojnih sila od naboja kugle. Ako se prenese u sferu (k − 1) dio naboja, tada je njegov potencijal jednak

Dakle, da bi se sljedeći dio naboja prenio na kuglu, potrebno je izvršiti rad

Ukupan rad na naelektrisanju kugle (jednak energiji električnog polja kugle) izražava se zbrojem geometrijske progresije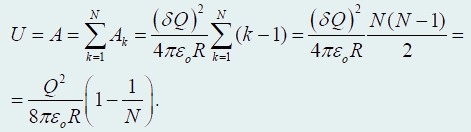

Očekivano, dobili smo izraz koji se u potpunosti podudara s (17), a beskonačnim smanjenjem udjela prenesenih naboja ponovno dolazimo do formule (14).
To nije iznenađujuće, budući da smo u prvom slučaju izračunali energiju koja će se osloboditi kada se naboji rasprše iz sfere, au drugom slučaju, energiju koju je potrebno utrošiti da ih se prikupi natrag.
Pokažimo da se energija međudjelovanja naboja u ovom slučaju može tumačiti i kao energija električnog polja, “razmazana” po cijelom prostoru u kojem polje postoji. Zamislimo da se polumjer sfere malo povećao ΔR, ali njegov naboj se nije promijenio. Prema formuli (14), energija međudjelovanja naboja će se smanjiti. U prostoru, izvan sfere povećanog radijusa, električno polje se nije promijenilo, ali je u tankom sfernom sloju između početne i proširene sfere nestalo (sl. 351).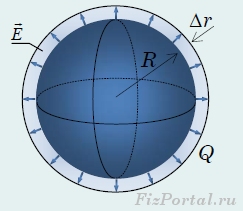

riža. 351
Stoga treba pretpostaviti da je smanjenje energije međudjelovanja naboja s povećanjem polumjera kugle jednako energiji sadržanoj u tom tankom sfernom sloju. Ako je debljina sloja mala, njegov volumen se može izračunati kao umnožak površine kugle i debljine sloja

Zanemarujući promjenu jakosti polja unutar tankog sloja, upisujemo energiju sadržanu u njemu u obliku

Gdje w− gustoća energije polja. S druge strane, ta je energija jednaka promjeni energije međudjelovanja naboja s povećanjem polumjera kugle

Na posljednji korak zanemarili smo malu promjenu radijusa ΔR. Na kraju, naboj kuglice izražavamo preko jakosti električnog polja na njezinoj površini

Zatim

Iz usporedbe s formulom (16) slijedi da je u razmatranom slučaju gustoća energije električnog polja izražena formulom