Szkoła Średnia MBOU nr 17, Iwanowo

« Równania z modułem”
Rozwój metodologiczny

Skompilowane

nauczyciel matematyki

Lebedeva N.V.

20010

Nota wyjaśniająca

Rozdział 1. Wprowadzenie

Rozdział 2. Podstawowe właściwości Rozdział 3. Interpretacja geometryczna pojęcia modułu liczby Rozdział 4. Wykres funkcji y = |x| Sekcja 5. Konwencje

Rozdział 2. Rozwiązywanie równań zawierających moduł

Rozdział 1. Równania postaci |F(x)| = m (najprostszy) Rozdział 2. Równania postaci F(|x|) = m Rozdział 3. Równania postaci |F(x)| = G(x) Rozdział 4. Równania postaci |F(x)| = ± F(x) (najpiękniejszy) Rozdział 5. Równania postaci |F(x)| = |G(x)| Rozdział 6. Przykłady rozwiązań równania niestandardowe Rozdział 7. Równania postaci |F(x)| + |G(x)| = 0 Rozdział 8. Równania postaci |a 1 x ± b 1 | ± |a 2 x ± w 2 | ± …|a n x ± w n | = m Rozdział 9. Równania zawierające kilka modułów

Rozdział 3. Przykłady rozwiązywania różnych równań modułowych.

Sekcja 1. Równania trygonometryczne Sekcja 2. Równania wykładnicze Sekcja 3. Równania logarytmiczne Rozdział 4. Równania niewymierne Sekcja 5. Zadania zaawansowane Odpowiedzi do ćwiczeń Referencje

Nota wyjaśniająca.

Pojęcie wartości bezwzględnej (modułu) liczby rzeczywistej jest jedną z jej podstawowych cech. Pojęcie to jest szeroko rozpowszechnione w różnych działach nauk fizycznych, matematycznych i technicznych. W praktyce nauczania przedmiotów matematycznych w szkołach średnich zgodnie z Programem Ministerstwa Obrony Federacji Rosyjskiej wielokrotnie spotyka się pojęcie „wartości bezwzględnej liczby”: w klasie szóstej definicja modułu i wprowadzono jego znaczenie geometryczne; w ósmej klasie powstaje pojęcie błędu bezwzględnego, rozważane jest rozwiązanie najprostszych równań i nierówności zawierających moduł oraz badane są właściwości arytmetycznego pierwiastka kwadratowego; w 11. klasie koncepcję tę można znaleźć w części „Root N-stopień." Doświadczenie dydaktyczne pokazuje, że uczniowie często napotykają trudności przy rozwiązywaniu zadań wymagających wiedzy tego materiału i często go pomijają, nie rozpoczynając jego wdrażania. Podobne zadania znajdują się także w tekstach zadań egzaminacyjnych dla klas IX i XI. Ponadto wymagania, jakie uczelnie stawiają absolwentom szkół, są różne, a mianowicie większe wysoki poziom niż wymagają tego szkolne programy nauczania. Dla życia we współczesnym społeczeństwie bardzo ważne jest ukształtowanie matematycznego stylu myślenia, przejawiającego się w niektórych umiejętnościach umysłowych. W procesie rozwiązywania problemów z modułami wymagana jest umiejętność stosowania technik takich jak uogólnianie i specyfikacja, analiza, klasyfikacja i systematyzacja oraz analogia. Rozwiązanie takich zadań pozwala sprawdzić swoją wiedzę z głównych sekcji kursu szkolnego, poziomu logiczne myślenie , wstępne umiejętności badawcze. Ta praca poświęcony jest jednemu z działów - rozwiązywaniu równań zawierających moduł. Składa się z trzech rozdziałów. W pierwszym rozdziale przedstawiono podstawowe pojęcia i najważniejsze rozważania teoretyczne. W drugim rozdziale zaproponowano dziewięć głównych typów równań zawierających moduł, omówiono metody ich rozwiązywania oraz zbadano przykłady o różnym stopniu złożoności. W trzecim rozdziale przedstawiono bardziej złożone i niestandardowe równania (trygonometryczne, wykładnicze, logarytmiczne i niewymierne). Dla każdego rodzaju równań znajdują się ćwiczenia niezależna decyzja (odpowiedzi i instrukcje w załączeniu). Głównym celem tej pracy jest zapewnienie nauczycielom pomocy metodycznej w przygotowaniu się do zajęć lekcyjnych i organizacji zajęć fakultatywnych. Materiał można wykorzystać także jako

pomoc dydaktyczna

dla uczniów szkół średnich. Zaproponowane w pracy zadania są ciekawe i nie zawsze łatwe do rozwiązania, co pozwala na uświadomienie motywacji edukacyjnej uczniów, sprawdzenie ich możliwości i podniesienie poziomu przygotowania absolwentów szkół do podjęcia studiów wyższych. Zróżnicowany dobór proponowanych ćwiczeń polega na przejściu od odtwórczego poziomu opanowania materiału do twórczego, a także daje możliwość nauczenia, jak zastosować zdobytą wiedzę przy rozwiązywaniu niestandardowych problemów. .

Rozdział 1. Wprowadzenie. : Rozdział 1. Wyznaczanie wartości bezwzględnej Definicja Wartość bezwzględna (moduł) liczby rzeczywistej Definicja A liczba nieujemna nazywana jest: Lub │ Definicja │ -A.

│ Oznaczenie:

│Wpis brzmi następująco: „moduł liczby a” lub „wartość bezwzględna liczby a”

│ a, jeśli a > 0
a│ = │ 0, jeśli a = 0 (1) 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

- i jeśli A

Przykłady:

Rozwiń moduł wyrażeń:

a) │x - 8│, jeśli x > 12 b) │2x + 3│, jeśli x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3 Rozdział 2. Podstawowe właściwości. Rozważmy podstawowe właściwości wartości bezwzględnej. Właściwość nr 1: Liczby przeciwne mają równe moduły, tj. │а│=│- а│ : │Pokażemy, że równość jest prawdziwa. Zapiszmy definicję liczby= (2) Porównajmy zbiory (1) i (2). Oczywiście definicje wartości bezwzględnych liczb Definicja I │а│=│- а│ mecz. Stąd, Właściwość nr 1:
Rozważając poniższe własności, ograniczymy się do ich sformułowania, gdyż podany jest ich dowód Właściwość nr 2: Wartość bezwzględna sumy skończonej liczby liczb rzeczywistych nie przekracza sumy wartości bezwzględnych wyrazów: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Właściwość nr 3: Wartość bezwzględna różnicy między dwiema liczbami rzeczywistymi nie przekracza sumy ich wartości bezwzględnych: │а - │ ≤│а│+│в│ Właściwość nr 4: Wartość bezwzględna iloczynu skończonej liczby liczb rzeczywistych jest równa iloczynowi wartości bezwzględnych czynników: │а·в│=│а│·│в│ Właściwość nr 5: Wartość bezwzględna ilorazu liczb rzeczywistych jest równa ilorazowi ich wartości bezwzględnych:

Rozdział 3. Interpretacja geometryczna pojęcia modułu liczby.

Każdą liczbę rzeczywistą można powiązać z punktem na osi liczbowej, który będzie obrazem geometrycznym tej liczby rzeczywistej. Każdy punkt na osi liczbowej odpowiada jego odległości od początku, tj. długość odcinka od początku do danego punktu. Odległość tę traktuje się zawsze jako wartość nieujemną. Zatem długość odpowiedniego odcinka będzie interpretacją geometryczną wartości bezwzględnej danej liczby rzeczywistej

Przedstawiona ilustracja geometryczna jednoznacznie potwierdza właściwość nr 1, tj. moduły liczb przeciwnych są równe. Stąd łatwo zrozumieć ważność równości: │х – а│= │а – x│. Rozwiązanie równania │х│= m, gdzie m ≥ 0, czyli x 1,2 = ± m, również staje się bardziej oczywiste. a│ = │ 0, jeśli a = 0 (1) 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; 4

Sekcja 4. Wykres funkcji y = │х│

Dziedziną tej funkcji są wszystkie liczby rzeczywiste.

Sekcja 5. Konwencje.

W przyszłości, rozważając przykłady rozwiązywania równań, zostaną wykorzystane następujące informacje symbolika: ( - znak systemu [ - znak całości Rozwiązując układ równań (nierówności), znajduje się przecięcie rozwiązań równań (nierówności) zawartych w układzie. Rozwiązując układ równań (nierówności), znajduje się sumę rozwiązań zawartych w układzie równań (nierówności).

Rozdział 2. Rozwiązywanie równań zawierających moduł.

W tym rozdziale przyjrzymy się algebraicznym metodom rozwiązywania równań zawierających jeden lub więcej modułów.

Rozdział 1. Równania postaci │F (x)│= m

Równanie tego typu nazywa się najprostszym. Ma rozwiązanie wtedy i tylko wtedy, gdy m ≥ 0. Z definicji modułu pierwotne równanie jest równoważne zbiorowi dwóch równań: │ F(x)│=M
a│ = │ 0, jeśli a = 0 (1)
№1. Rozwiąż równanie: │7х - 2│= 9


Odpowiedź: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

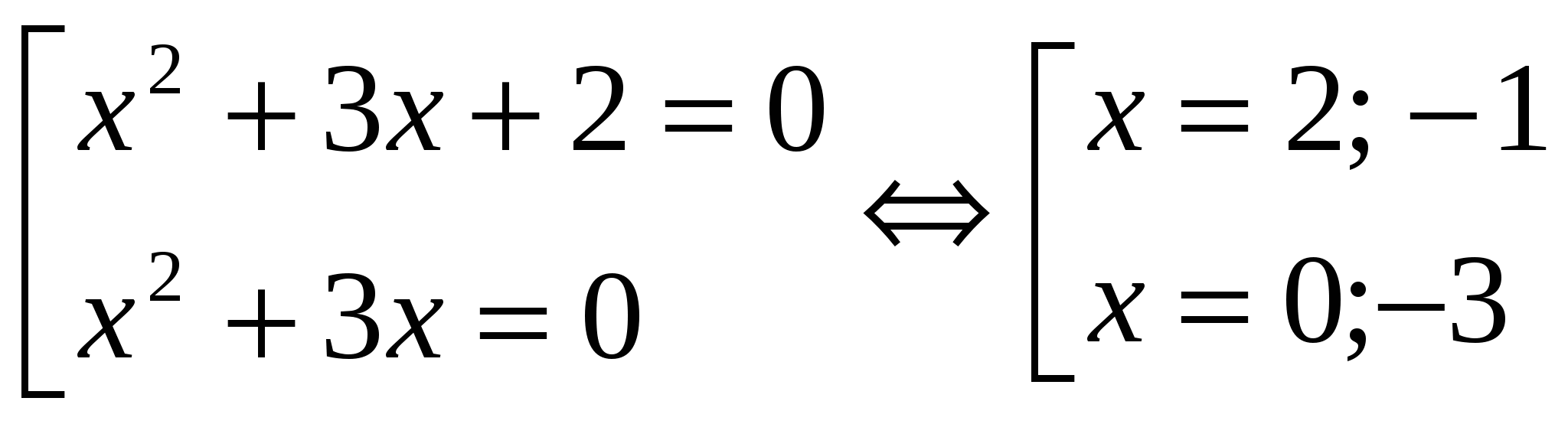x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Odpowiedź: suma pierwiastków wynosi - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 oznaczmy x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5 m + 4 = 0 m = 1; 4 – obie wartości spełniają warunek m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Odpowiedź: liczba pierwiastków równania 7. Ćwiczenia:
№1. Rozwiąż równanie i wskaż sumę pierwiastków: │х - 5│= 3 №2 . Rozwiąż równanie i wskaż mniejszy pierwiastek: │x 2 + x│= 0 №3 . Rozwiąż równanie i wskaż większy pierwiastek: │x 2 – 5x + 4│= 4 №4 .Rozwiąż równanie i wskaż cały pierwiastek: │2x 2 – 7x + 6│= 1 №5 .Rozwiąż równanie i wskaż liczbę pierwiastków: │x 4 – 13x 2 + 50│= 14

Sekcja 2. Równania postaci F(│х│) = m

Argument funkcji po lewej stronie znajduje się pod znakiem modułu, a prawa strona jest niezależna od zmiennej. Rozważmy dwa sposoby rozwiązywania równań tego typu. 1 sposób: Z definicji wartości bezwzględnej pierwotne równanie jest równoważne kombinacji dwóch systemów. W każdym z nich na wyrażenie submodularne nałożony jest warunek. F(│х│) =M
Ponieważ funkcja F(│x│) jest parzysta w całym obszarze definicji, pierwiastkami równań F(x) = m i F(- x) = m są pary liczb przeciwnych. Wystarczy zatem rozwiązać jeden z układów (rozważając w ten sposób przykłady podane zostanie rozwiązanie dla jednego układu). Metoda 2: Zastosowanie metody wprowadzania nowej zmiennej. W tym przypadku wprowadza się oznaczenie │x│= a, gdzie a ≥ 0. Metoda ta jest mniej obszerna w projektowaniu.
a│ = │ 0, jeśli a = 0 (1) №1 . Rozwiąż równanie: 3x 2 – 4│x│= - 1 Skorzystajmy z wprowadzenia nowej zmiennej. Oznaczmy │x│= a, gdzie a ≥ 0. Otrzymujemy równanie 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Wróć do zmiennej wyjściowej: │ x│=1 i │х│= 1/3. Każde równanie ma dwa pierwiastki. Odpowiedź: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Rozwiąż równanie: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
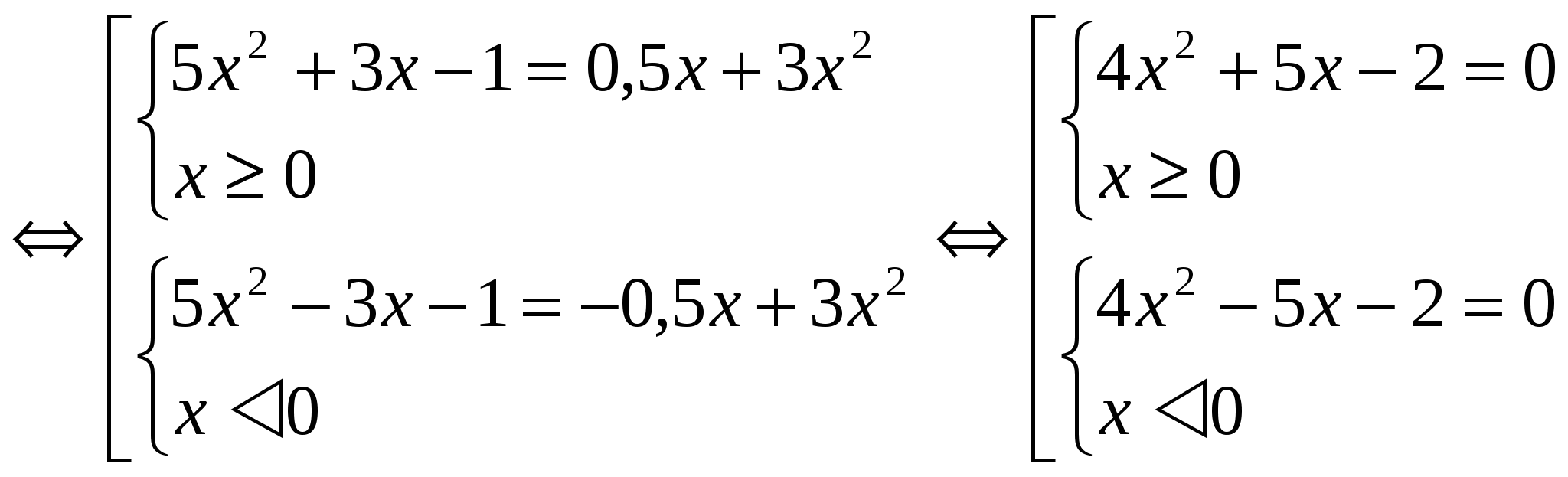Znajdźmy rozwiązanie pierwszego układu populacji: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Zauważ, że x 2 nie spełnia warunek x ≥ 0. Rozwiązaniem drugim systemem będzie liczba przeciwna do wartości x 1. Odpowiedź: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Rozwiąż równanie: x 4 – │х│= 0 Oznaczmy │х│= a, gdzie a ≥ 0. Otrzymujemy równanie a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Powrót do pierwotnej zmiennej: │х│=0 i │х│= 1 x = 0; ± 1 Odpowiedź: x 1 = 0; X 2 = 1; X 3 = - 1.
Ćwiczenia: №6. Rozwiąż równanie: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Rozwiąż równanie, wskaż liczbę pierwiastków w swojej odpowiedzi: 3x 2 - 7│x│ + 2 = 0 №8 . Rozwiąż równanie, w odpowiedzi wskaż rozwiązania całkowite: x 4 + │x│ - 2 = 0

Rozdział 3. Równania postaci │F(x)│ = G(x)

Prawa strona równania tego typu zależy od zmiennej i dlatego ma rozwiązanie wtedy i tylko wtedy, gdy prawa strona jest funkcją G(x) ≥ 0. Oryginalne równanie można rozwiązać na dwa sposoby : 1 sposób: Standard polega na ujawnieniu modułu w oparciu o jego definicję i polega na równoważnym przejściu do kombinacji dwóch systemów. │ F(x)│ =G(X)

Metodę tę można racjonalnie zastosować w przypadku wyrażenia złożonego dla funkcji G(x) i mniej złożonego dla funkcji F(x), gdyż zakłada się, że nierówności z funkcją F(x) zostaną rozwiązane. Metoda 2: Polega na przejściu do układu równoważnego, w którym po prawej stronie nałożony jest warunek. │ F(X)│= G(X)

Metoda ta jest wygodniejsza w użyciu, jeśli wyrażenie na funkcję G(x) jest mniej złożone niż na funkcję F(x), gdyż zakłada się, że nierówność G(x) ≥ 0 została rozwiązana w przypadku kilku modułów w tej metodzie zaleca się użycie drugiej opcji. a│ = │ 0, jeśli a = 0 (1) №1. Rozwiąż równanie: │x + 2│= 6 -2x
(1 sposób) Odpowiedź: x = 1 1 / 3 №2.
│х 2 – 2х - 1│= 2·(x + 1)
(dwukierunkowy) Odpowiedź: Iloczyn pierwiastków wynosi 3.
№3. Rozwiąż równanie i wskaż sumę pierwiastków w swojej odpowiedzi:
│x - 6│= x 2 - 5x + 9

Odpowiedź: suma pierwiastków wynosi 4.
Ćwiczenia: №9. │x + 4│= - 3x №10. Rozwiąż równanie, wskaż liczbę rozwiązań w swojej odpowiedzi:│x 2 + x - 1│= 2x – 1 №11 . Rozwiąż równanie, wskaż iloczyn pierwiastków w swojej odpowiedzi:│x + 3│= x 2 + x – 6

Rozdział 4. Równania postaci │F(x)│= F(x) i │F(x)│= - F(x)

Równania tego typu nazywane są czasami „najpiękniejszymi”. Ponieważ prawa strona równań zależy od zmiennej, rozwiązania istnieją wtedy i tylko wtedy, gdy prawa strona jest nieujemna. Zatem pierwotne równania są równoważne nierównościom:
│F(x)│= F(x) F(x) ≥ 0 i │F(x)│= - F(x) F(x) a│ = │ 0, jeśli a = 0 (1) №1 . Rozwiąż równanie, w odpowiedzi wskaż mniejszy cały pierwiastek: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Odpowiedź: x = 1№2. Rozwiąż równanie, wskaż długość przedziału w swojej odpowiedzi: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Odpowiedź: długość odcinka wynosi 6.№3 . Rozwiąż równanie i wskaż liczbę rozwiązań całkowitych w swojej odpowiedzi: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Odpowiedź: 4 całe rozwiązania.№4 . Rozwiąż równanie i wskaż największy pierwiastek swojej odpowiedzi:
│4 – x -
│= 4 – x –
x 2 – 5x + 5 = 0 D = 5 x 1,2 =
≈ 1,4

Odpowiedź: x = 3.

Ćwiczenia: №12. Rozwiąż równanie, w odpowiedzi wskaż cały pierwiastek: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Rozwiąż równanie i wskaż liczbę rozwiązań całkowitych w swojej odpowiedzi: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Rozwiąż równanie; w swojej odpowiedzi wskaż liczbę całkowitą, która nie jest pierwiastkiem równania:

Rozdział 5. Równania postaci │F(x)│= │G(x)│

Ponieważ obie strony równania są nieujemne, rozwiązanie polega na rozważeniu dwóch przypadków: wyrażenia submodularne mają znak równy lub przeciwny. Dlatego oryginalne równanie jest równoważne kombinacji dwóch równań: │ F(X)│= │ G(X)│
a│ = │ 0, jeśli a = 0 (1) №1. Rozwiąż równanie, w odpowiedzi wskaż cały pierwiastek: │x + 3│=│2x - 1│
Odpowiedź: cały pierwiastek x = 4.№2. Rozwiąż równanie: │ x – x 2 - 1│=│2x – 3 – x 2 │
Odpowiedź: x = 2.№3 . Rozwiąż równanie i wskaż iloczyn pierwiastków w swojej odpowiedzi:




Równania pierwiastkowe 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Odpowiedź: iloczyn pierwiastków wynosi – 0,25. Ćwiczenia: №15 . Rozwiąż równanie i wskaż całe rozwiązanie w swojej odpowiedzi: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Rozwiąż równanie, wskaż mniejszy pierwiastek w swojej odpowiedzi:│5x - 3│=│7 - x│ №17 . Rozwiąż równanie i wskaż sumę pierwiastków w swojej odpowiedzi:

Rozdział 6. Przykłady rozwiązywania równań niestandardowych

W tej sekcji rozważymy przykłady niestandardowych równań, przy rozwiązywaniu których z definicji ujawnia się wartość bezwzględna wyrażenia. a│ = │ 0, jeśli a = 0 (1)

№1. Rozwiąż równanie, wskaż sumę pierwiastków w swojej odpowiedzi: x · │x│- 5x – 6 = 0
Odpowiedź: suma pierwiastków wynosi 1 №2. . Rozwiąż równanie, wskaż mniejszy pierwiastek w swojej odpowiedzi: x 2 - 4x ·
- 5 = 0
Odpowiedź: mniejszy pierwiastek x = - 5. №3. Rozwiąż równanie:

Odpowiedź: x = -1. Ćwiczenia: №18. Rozwiąż równanie i wskaż sumę pierwiastków: x · │3x + 5│= 3x 2 + 4x + 3
№19. Rozwiąż równanie: x 2 – 3x =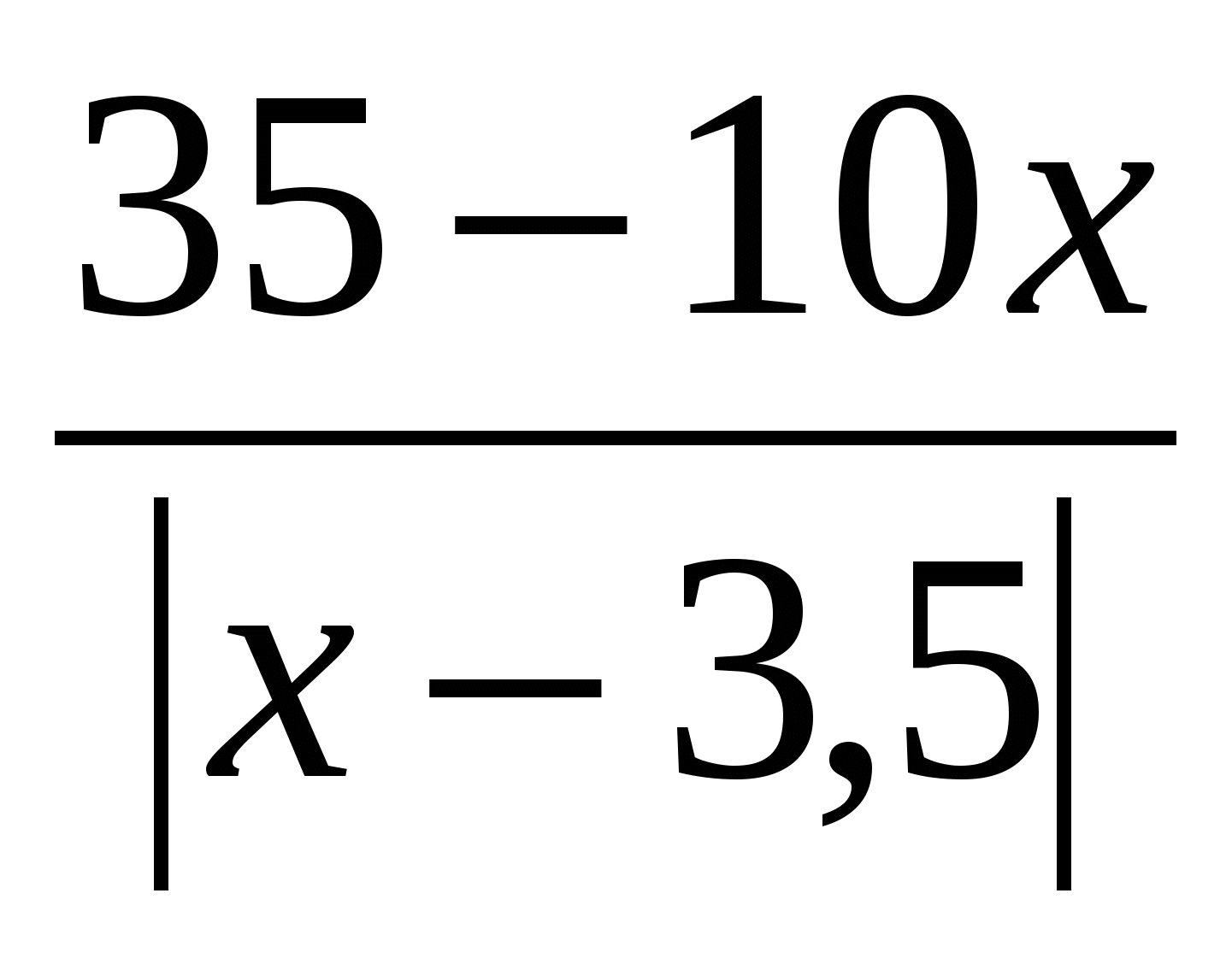

№20. Rozwiąż równanie:

Rozdział 7. Równania postaci │F(x)│+│G(x)│=0

Łatwo zauważyć, że po lewej stronie równania tego typu znajduje się suma wielkości nieujemnych. Dlatego pierwotne równanie ma rozwiązanie wtedy i tylko wtedy, gdy oba wyrazy są jednocześnie równe zero. Równanie jest równoważne układowi równań: │ F(X)│+│ G(X)│=0
a│ = │ 0, jeśli a = 0 (1) №1 . Rozwiąż równanie:
Odpowiedź: x = 2. №2. Rozwiąż równanie: Odpowiedź: x = 1. Ćwiczenia: №21. Rozwiąż równanie: №22 . Rozwiąż równanie i wskaż sumę pierwiastków w swojej odpowiedzi: №23 . Rozwiąż równanie i wskaż liczbę rozwiązań w swojej odpowiedzi:

Sekcja 8. Równania postaci │a 1 x + b 1 │±│a 2 x + b 2 │± ... │a n x +b n │= m

Do rozwiązywania równań tego typu stosuje się metodę przedziałową. Jeśli rozwiążemy to poprzez sekwencyjne rozszerzanie modułów, otrzymamy N zestawów systemów, co jest bardzo kłopotliwe i niewygodne. Rozważmy algorytm metody przedziałowej: 1). Znajdź wartości zmiennych X, dla którego każdy moduł jest równy zeru (zera wyrażeń submodularnych):
2). Zaznacz znalezione wartości na osi liczbowej, która jest podzielona na przedziały (liczba przedziałów jest odpowiednio równa N+1 ) 3). Określ, jakim znakiem ujawnia się każdy moduł w każdym z powstałych odstępów (przy formułowaniu rozwiązania możesz użyć osi liczbowej, zaznaczając na niej znaki) 4). Oryginalne równanie jest równoważne agregatowi N+1 systemów, w każdym z których wskazana jest przynależność zmiennej X jeden z interwałów. a│ = │ 0, jeśli a = 0 (1) №1 . Rozwiąż równanie i wskaż największy pierwiastek swojej odpowiedzi:
1). Znajdźmy zera wyrażeń submodularnych: x = 2; x = -3 2). Zaznaczmy znalezione wartości na osi liczbowej i określmy, jakim znakiem ujawnia się każdy moduł w uzyskanych przedziałach:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- brak rozwiązań Równanie ma dwa pierwiastki. Odpowiedź: największy pierwiastek x = 2. №2. Rozwiąż równanie i podaj cały pierwiastek w swojej odpowiedzi:
1). Znajdźmy zera wyrażeń submodularnych: x = 1,5; x = - 1 2). Zaznaczmy znalezione wartości na osi liczbowej i ustalmy, jakim znakiem ujawnia się każdy moduł w uzyskanych przedziałach: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
Ostatni układ nie ma rozwiązań, dlatego równanie ma dwa pierwiastki. Rozwiązując równanie należy zwrócić uwagę na znak „-” znajdujący się przed drugim modułem. Odpowiedź: cały pierwiastek x = 7. №3. Rozwiąż równanie, wskaż sumę pierwiastków w swojej odpowiedzi: 1). Znajdźmy zera wyrażeń submodularnych: x = 5; x = 1; x = - 2 2). Zaznaczmy znalezione wartości na osi liczbowej i ustalmy, jakim znakiem ujawnia się każdy moduł w otrzymanych odstępach: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Równanie ma dwa pierwiastki x = 0 i 2. Odpowiedź: suma pierwiastków wynosi 2. №4 . Rozwiąż równanie: 1). Znajdźmy zera wyrażeń submodularnych: x = 1; x = 2; x = 3. 2). Ustalmy, jakim znakiem ujawnia się każdy moduł na otrzymanych przedziałach. 3).
Połączmy rozwiązania pierwsze trzy systemy Odpowiedź: ; x = 5.
Ćwiczenia: №24. Rozwiąż równanie:
№25. Rozwiąż równanie i wskaż sumę pierwiastków w swojej odpowiedzi: №26. Rozwiąż równanie i wskaż mniejszy pierwiastek swojej odpowiedzi: №27. Rozwiąż równanie i wskaż większy pierwiastek swojej odpowiedzi:

Rozdział 9. Równania zawierające kilka modułów

Równania zawierające wiele modułów zakładają obecność wartości bezwzględnych w wyrażeniach submodularnych. Podstawową zasadą rozwiązywania równań tego typu jest sekwencyjne ujawnianie modułów, zaczynając od „zewnętrznego”. Podczas rozwiązywania stosowane są techniki omówione w rozdziałach nr 1, nr 3.

a│ = │ 0, jeśli a = 0 (1) №1. Rozwiąż równanie:
Odpowiedź: x = 1; - 11. №2. Rozwiąż równanie:
Odpowiedź: x = 0; 4; - 4. №3. Rozwiąż równanie i wskaż iloczyn pierwiastków w swojej odpowiedzi:
Odpowiedź: iloczyn pierwiastków wynosi – 8. №4. Rozwiąż równanie:
Oznaczmy równania populacji (1) I (2) i rozważ rozwiązanie dla każdego z nich osobno, aby ułatwić projektowanie. Ponieważ oba równania zawierają więcej niż jeden moduł, wygodniej jest przeprowadzić równoważne przejście do zbiorów układów. (1)

(2)


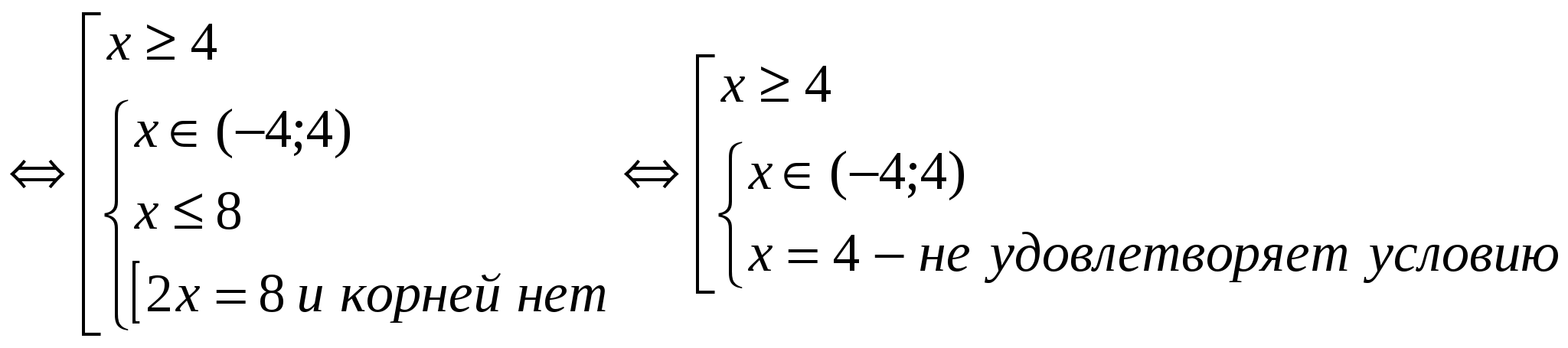Odpowiedź:
Ćwiczenia: №36. Rozwiąż równanie, wskaż sumę pierwiastków w swojej odpowiedzi: 5 │3x-5│ = 25 x №37. Rozwiąż równanie, jeśli jest więcej niż jeden pierwiastek, w odpowiedzi wskaż sumę pierwiastków: │x + 2│ x – 3x – 10 = 1 №38. Rozwiąż równanie: 3 │2x -4│ = 9 │x│ №39. Rozwiąż równanie, w swojej odpowiedzi podaj liczbę pierwiastków na: 2 │ sin x│ = √2 №40 . Rozwiąż równanie i wskaż liczbę pierwiastków w swojej odpowiedzi:

Rozdział 3. Równania logarytmiczne.

Przed rozwiązaniem poniższych równań należy zapoznać się z właściwościami logarytmów i funkcją logarytmiczną. a│ = │ 0, jeśli a = 0 (1) №1. Rozwiąż równanie, w odpowiedzi wskaż iloczyn pierwiastków: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

Przypadek 1: jeśli x ≥ - 1, to log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – spełnia warunek x ≥ - 1 2 przypadek: jeśli x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – spełnia warunek x - 1
Odpowiedź: iloczyn pierwiastków wynosi – 15.
№2. Rozwiąż równanie, wskaż sumę pierwiastków w swojej odpowiedzi: lg
O.D.Z.

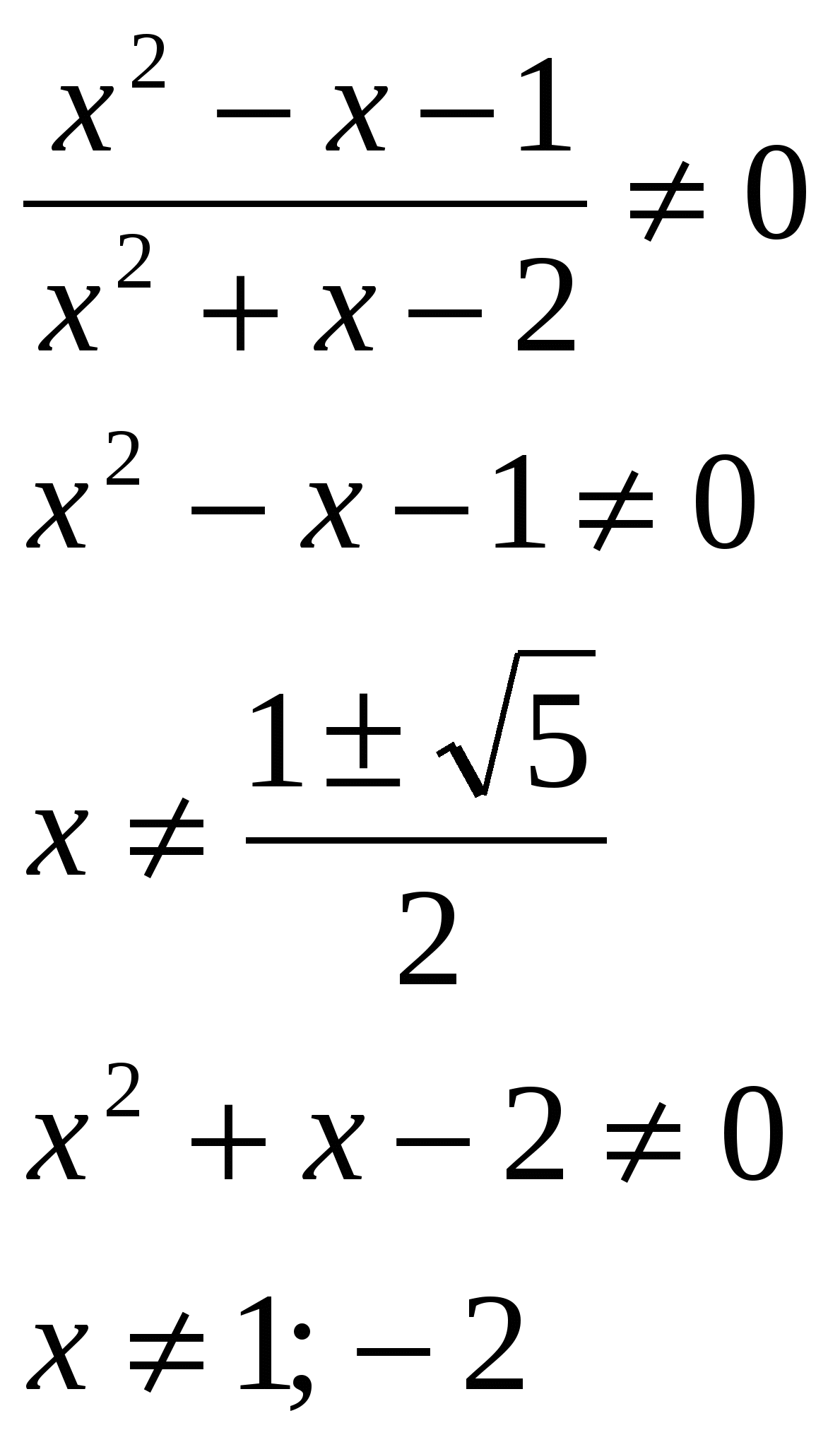
Odpowiedź: suma pierwiastków wynosi 0,5.
№3. Rozwiąż równanie: log 5
O.D.Z.

Odpowiedź: x = 9. №4. Rozwiąż równanie: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Skorzystajmy ze wzoru na przejście do innej bazy. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Znajdźmy zera wyrażeń submodularnych: x = 25; x = Te liczby dzielą obszar dopuszczalne wartości na trzy przedziały, więc równanie jest równoważne zbiorowi trzech układów.
Odpowiedź: )