Як вирішувати комплексні числа? Комплексні числа для чайників
ІЗОЛЬОВАНІ ОСОБЛИВІ ТОЧКИ
КОМПЛЕКСНІ ЧИСЛА І ДІЇ НАД НИМИ
Вже найпростіші операції алгебри над дійсними числами (вилучення квадратного кореня з негативного числа, рішення квадратного рівняння з негативним дискримінантом) виводять за межі безлічі дійсних чисел. Подальше узагальнення поняття числа призводить до комплексних чисел. Чудовою властивістю безлічі комплексних чисел є його замкнутість щодо основних математичних операцій. Інакше кажучи, основні математичні операціїнад комплексними числами не виводять із безлічі комплексних чисел.
Комплексним числом (в формі алгебри ) називається вираз
де - довільні дійсні числа, - уявна одиниця , обумовлена умовою.
Число називається дійсною частиною комплексного числа , позначається (від латинського « realis»), число називається уявною частиною комплексного числа та позначається (від латинського « imaginarius»).
Два комплексних числа і рівні тоді й лише тоді, коли рівні їх дійсні та уявні частини: , . Два комплексних числа рівні або рівні (поняття «більше» і «менше» для комплексних чисел не вводяться).
Комплексно-сполученим до числа називається число . Вочевидь, комплексно-спряженное число до збігається з числом : .
Арифметичні операції.Додавання, віднімання та множення комплексних чисел виробляють за звичайним правиламалгебри.
Нехай,. Тоді
різниця ,
твір ,
приватне (при )
Приклад 1. Задано комплексні числа, .
Знайти , , .
Рішення. ;
Завдання 1. Нехай і – пара комплексно-сполучених чисел. Показати, що й сума є дійсне число, різниця - уявне число, а твір є дійсне неотрицательное число.
Приклад 2. Знайти , .
Рішення. ; .
Зауваження.Ступені числа можна подати у вигляді таблиці
приклад 3.Перемножити числа та .
Рішення.
приклад 4.Обчислити а); б); в).
Рішення.
а) Розкриємо квадрат різниці:
б) Розкриємо куб суми:
Приклад 5.Знайти приватне, якщо.
Рішення.
Приклад 6.Обчислити а), б).
Рішення. а) .
Запам'ятаємо:
Геометрична інтерпретація комплексного числа.
Розглянемо декартову прямокутну систему координат. Відкладемо по осі абсцис дійсну частину комплексного числа, а по осі ординат - його уявну частину. Отримаємо точку з координатами. У цьому кожному комплексному числу відповідає одна точка площині. Правильне і зворотне: кожній точці площини можна поставити у відповідність комплексне число , дійсна частина якого дорівнює абсцисі точки, а уявна частина дорівнює ординаті точки. Таким чином, між комплексними числами та точками площини встановлюється взаємно однозначна відповідність. (Раніше ми говорили про взаємно однозначну відповідність між дійсними числами і точками числової прямої).
Площина, точки якої зображують комплексні числа, називається комплексною площиною. Для відмінність її від дійсної площини у правому верхньому куткупишуть букву, обведену гуртком. Вісь абсцис на такій площині називають справжньою віссю, а вісь ординат - уявною віссю. Комплексно-сполучене число – це дзеркальне відображення заданого комплексного числа щодо дійсної осі. Початок координат називається нуль-точкою. Відстань комплексного числа від початку координат називається модулем цього числа:
Завдання 2.Довести, що .
Модуль різниці двох комплексних чисел – це відстань між відповідними точками:
Кожній точці комплексної площини поставимо у відповідність вектор з початком у нуль-точці та кінцем у цій точці. Очевидно, ця відповідність є взаємно однозначною. У такій інтерпретації дійсна та уявна частини комплексного числа – це перша та друга компоненти вектора. Сума представляється тепер діагоналлю паралелограма, побудованого на векторах і , різниця розуміється як . Модуль комплексного числа є довжиною вектора. Геометрично очевидним є нерівність трикутника у комплексній площині: .
Приклад 7.Вказати геометричне місце точок на комплексній площині, для яких
| а); | б); |
| в); | г). |
Рішення. а) Оскільки , то задану подвійну нерівність можна переписати як: . Отримали вертикальну смугу.
б) Оскільки , то задану подвійну нерівність перепишемо як: . Отримали горизонтальну смугу. Завдання в) та г) вирішити самостійно.
Приклад 8.
Рішення. а) Модуль комплексного числа - це довжина вектора, що йде з нуль-точки в точку, тобто. відстань від початку координат до точки. Отже, у разі йдеться про геометричне місце точок площини, рівновіддалених від початку координат - це коло (у даному випадку радіус кола дорівнює 1). Можна було перекласти завдання мовою декартових координат:
б) Тут йдеться про геометричне місце точок, що знаходяться поза кола радіусу (з центром на початку координат).
в) точки знаходяться в кільці між колами радіусу та .
Приклад 9.Вказати геометричне місце точок на комплексній площині, для яких а); б); в).
Рішення. а) Модуль різниці - це відстань між точкою комплексної площини і точкою 1. Отже, йдеться про геометричне місце точок, рівновіддалених (на відстань 1) від точки 1, - це коло радіуса 1 з центром у точці (1; 0). Мовою координат:
б) Крапки знаходяться одночасно у колі з центром на початку координат та у колі з центром, зміщеним у точку: .
в) Це точки правої полуплоскости , що усередині кола : .
Тригонометрична форма комплексного числа. Аргументом комплексного числа називають кут , що становить вектор з позитивним напрямом дійсної осі, . Цей кут визначається неоднозначно:
Тут - головне значення аргументу, воно виділяється нерівностями (тобто. на комплексній площині проводиться розріз по справжній осі вліво від початку координат).
У першому стовпці вказаний для числа , що лежить на дійсній або уявній осі, а в другому стовпці - для решти всіх комплексних чисел.
Позначимо. Оскільки , , то комплексне число можна уявити у тригонометричній формі :
Два комплексні числа і , задані в тригонометричній формі
з неоднозначності аргументу рівні тоді й лише тоді, коли , .
приклад 10.Знайти модулі та аргументи, а також головні значення аргументів комплексних чисел . Записати кожну з них у тригонометричній формі.
Рішення. Модулі всіх цих чисел однакові:
Аргумент кожного числа знаходимо з огляду на чверть, у якій лежить відповідна точка.
1) Крапка лежить у першій чверті, отже,
У тригонометричній формі тут врахована - періодичність косинуса і синуса.
2) Крапка лежить у другій чверті, отже,
3) Крапка лежить у третій чверті, отже,
4) Крапка лежить у четвертій чверті, отже,
Множення та розподіл комплексних чисел у тригонометричній формі.Нехай числа та задані у тригонометричній формі: , . Перемножимо їх:
Згадуючи формули для косинуса та синуса суми двох кутів, отримуємо
Ми, що з множенні комплексних чисел їх модулі перемножуються, а аргументи складаються. Геометричний зміст цієї операції: представляючи числа та векторами на комплексній площині, що виходять з нуль-точки, бачимо, що вектор виходить із вектора «розтягуванням» у раз і поворотом на кут.
Для часткового отримуємо формулу:
Приклад 11.Знайти твір та приватне чисел
Рішення. Відповідно до формули (1) запишемо:
Перевіримо результат, перемножуючи ці числа в формі алгебри:
За формулою (2) знаходимо
У формі алгебри ця операція запишеться так:
Зведення комплексного числа до ступеня.З формули (1) випливає, що зведення в ступінь комплексного числа здійснюється за правилом
приклад 12.Обчислити 1); 2).
Рішення. 1) Вище ми отримали запис комплексного числа в тригонометричній формі: . За формулою (3) знаходимо . Той самий результат був отриманий вище в прикладі 4в) за допомогою бінома Ньютона.
2) Насамперед уявімо число в тригонометричній формі.
точка лежить у четвертій чверті, отже, . Тому
Залишається скористатися формулою (3):
Розкриваючи куб різниці, отримаємо той самий результат (перевірте!).
При формула (3) перетворюється на формулу Муавра :
З її допомогою легко виходять співвідношення, що виражають синуси та косинуси кратних кутів з і .
приклад 13.Виразити через і .
Рішення. Вважаючи у формулі Муавра, отримаємо:
Зліва розкриємо куб суми та зберемо подібні члени:
Тут враховано, що . Прийшли до рівності двох комплексних чисел в формі алгебри
яке справедливе в тому і тільки в тому випадку, коли дорівнюють дійсні та уявні частини цих чисел.
Рівність дійсних елементів дає;
прирівнюючи уявні частини, отримуємо .
Вилучення кореня з комплексного числа.Якщо комплексні числа пов'язані співвідношенням , то . Представимо числа та у тригонометричній формі:
Наше завдання - за заданим числом (тобто за відомими і) визначити (тобто і). Відповідно до формули (3) рівність запишеться у вигляді
З рівності двох комплексних чисел у тригонометричній формі випливає:
Тут - корінь ступеня з дійсного невід'ємного числа. Значить, для кореня ступеня з комплексного числа отримуємо формулу
Вважаючи послідовно, отримаємо різних значень:
Усі це коріння мають однакові модулі , тобто . відповідні точки розташовуються на колі радіусу з центром на початку координат. Аргументи двох сусідніх коренів відрізняються на кут. Отже, всі значення кореня ступеня з комплексного числа знаходяться у вершинах правильного кутника, вписаного в коло радіусу.
приклад 14.Знайти всі значення кореня ступеня з комплексного числа і зобразити їх на комплексній площині, якщо. Зауважимо, що і при. . Отримали два комплексно-сполучені корені.
Приклади з рішенням комплексних чисел дано наприкінці статті, а поки що розберемося з тим, що таке комплексні числа.
У математиці крім натуральних, раціональних та речових чисел є ще один вид, званий комплексними числами. Така множина прийнята позначати символом.
Розглянемо, що з себе є комплексним числом. Запишемо його таким чином: , в якому уявна одиниця , числа речові.
Якщо покласти, то комплексне число перетворюється на речове. Таким чином, можна дійти невтішного висновку, що дійсні числа це окремий випадоккомплексних і записати це у вигляді підмножини. До речі також можливо, що.
Прийнято записувати уявну частину комплексного числа як таку, а дійсну.
Введемо поняття комплексно-сполучених чисел. До кожного комплексного числа існує таке, що і називається сполученим. Такі числа відрізняються один від одного лише знаками між дійсною та уявною частиною.
Форма комплексного числа
Так склалося у математиці, що з цих чисел кілька форм. Число одне й теж, але записати його можна по-різному:
- Алгебраїчна
- Показова
- Тригонометрична
Зображення комплексних чисел
Вивчення вище ми почали з алгебраїчної форми. Тому що вона є основною. Щоб було зрозуміло у цій формі зобразимо комплексне число на площині:
Бачимо, що розташовані на відповідних осях площини.
Комплексне число представляється як вектора.
Аргумент позначається.
Модуль дорівнює довжині вектора і знаходиться за формулою
Аргумент комплексного числа потрібно знаходити за різними формулами в залежності від напівплощини, в якій лежить саме число.
Операції над комплексними числами
Над комплексними числами можна проводити різні операції, а саме:
- Складати та віднімати
- Примножувати та ділити
- Видобувати коріння та зводити у ступінь
- Перекладати з однієї форми в іншу
Для знаходження суми та різниціскладається і віднімаються лише відповідні один одному члени. Уявна частина тільки з уявною, а дійсна тільки з дійсної:
Розмноження в формі алгебри:
Розмноження у показовій формі:
Розподіл в формі алгебри:
Поділ у показовій формі:
Для зведення у ступіньнеобхідно помножити комплексне число саме на себе необхідна кількістьраз, або скористатися формулою Муавра:
Для вилучення коренівнеобхідно також скористатися формулою Муавра:
Також теорія комплексних чисел допомагає шукати коріння многочленов. Наприклад, в квадратному рівнянні, якщо, то речових коренів немає, але є комплексні. В останньому прикладі розглянуто цей випадок.
Розглянемо практично комплексні числа: приклади з рішенням.
Приклади із рішенням
| Приклад 4 |
| Звести комплексне число до ступеня: a) б) |
| Рішення |
|
Для зведення в квадрат досить помножити число саме на себе: Користуємося формулою для множення, розкриваємо дужки та наводимо такі: Отримали відповідь, що У цьому випадку не все так просто, як у попередньому випадку, коли було зведення в квадрат. Звичайно, можна вдатися до способу озвученого раніше і помножити число саме на себе 7 разів, але це буде дуже довге і довге рішення. Набагато простіше скористатися формулою Муавра. Але вона працює з числами у тригонометричній формі, а число задано в алгебраїчній. Отже, насамперед переведемо з однієї форми до іншої. Обчислюємо значення модуля: Знайдемо чим дорівнює аргумент: Записуємо у тригонометричному вигляді: Зводимо до ступеня: Перетворимо на форму алгебри для наочності: |
| Відповідь |
У статті " Комплексні числа: приклади з рішенням" було дано визначення, основні поняття, форми запису, операції алгебри та рішення практичних прикладів.
Ми познайомимося з поняттям комплексного числа, розглянемо алгебраїчну, тригонометричну та показову форму комплексного числа. А також навчимося виконувати дії з комплексними числами: додавання, віднімання, множення, розподіл, зведення у ступінь та витяг коріння. Не турбуйтесь, я вас налякав, я вас і розсмішить. Для освоєння комплексних чисел достатньо вміти виконувати основні алгебраїчні дії зі «звичайними» числами, і трохи знати тригонометрію.
1) Поняття комплексного числа. 2) Алгебраїчна форма комплексного числа. Додавання, віднімання, множення та розподіл комплексних чисел. 3) Тригонометрична та показова форма комплексного числа. 4) Зведення комплексних чисел на ступінь. 5) Вилучення коренів із комплексних чисел. Квадратне рівняння з комплексним корінням.
Спочатку згадаємо «звичайні» шкільні числа. У математиці вони називаються безліччю дійсних чиселі позначаються буквою (у літературі, рукописах велику букву «ер» пишуть жирної чи потовщеної). Усі дійсні числа зображуються на числовій прямій:
Компанія дійсних чисел дуже строката - тут і цілі числа, і дроби, і ірраціональні числа. При цьому кожній числовій точці обов'язково відповідає деяке дійсне число.
Поняття комплексного числа
Перш ніж ми перейдемо до розгляду комплексних чисел, дам важлива порада: не намагайтеся уявити комплексне число «в житті» – це все одно, що намагатися уявити четвертий вимір у нашому тривимірному просторі. Якщо хочете, комплексне число – це двовимірне число.
Комплексним числом називається число виду , де і – дійсні числа – так звана уявна одиниця. Число називається дійсною частиною ( ) комплексного числа , число називається уявною частиною ( ) комплексного числа.
- це ЄДИНЕ ЧИСЛО, а не додавання. Дійсну та уявну частини комплексного числа, в принципі, можна переставити місцями: або переставити уявну одиницю: – від цього комплексне число не зміниться. Але стандартно комплексне число прийнято записувати саме в такому порядку:
Щоб усе було зрозуміліше, одразу наведемо геометричну інтерпретацію. Комплексні числа зображуються на комплексної площини:
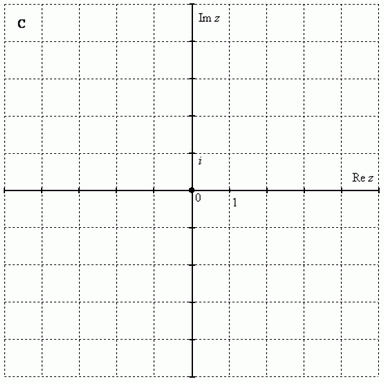Як згадувалося вище, буквою прийнято позначати безліч дійсних чисел. Безлічж комплексних чиселприйнято позначати «жирною» або потовщеною літерою. Тому на кресленні слід поставити літеру, позначаючи той факт, що ми маємо комплексну площину.
Комплексна площина складається з двох осей: - дійсна вісь, - уявна вісь
Правила оформлення креслення практично такі самі, як і для креслення в декартовій системі. По осях потрібно задати розмірність, відзначаємо: нуль; одиницю по дійсній осі; уявну одиницю по уявній осі.
Побудуємо на комплексній площині такі комплексні числа (див. стор 3):
За яким принципом відзначені числа на комплексній площині, гадаю, очевидно - комплексні числа відзначають так само, як ми відзначали точки ще в 5-6 класі на уроках геометрії.
Розглянемо такі комплексні числа: , , . Ви скажете, та це ж прості дійсні числа! І будете майже праві. Справжні числа – це окремий випадок комплексних чисел. Справжня вісь означає точно безліч дійсних чисел , тобто на осі сидять всі наші «звичайні» числа. Суворіше твердження можна сформулювати так: Безліч дійсних чисел є підмножиною безлічі комплексних чисел .
Числа , , - Це комплексні числа з нульовою уявною частиною. Числа , , – це, навпаки, чисто уявні числа, тобто. числа з нульовою дійсною частиною. Вони розташовуються строго на уявній осі.
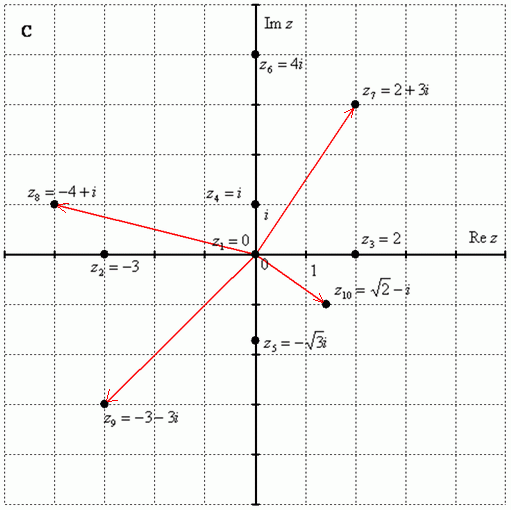
У числах , , , і дійсна і уявна частини не дорівнюють нулю. Такі числа теж позначаються точками на комплексній площині, причому до них прийнято проводити радіус-вектори з початку координат (позначені червоним кольором на кресленні). Радіус-вектори до чисел, які розташовуються на осях, зазвичай не креслять, тому що вони зливаються з осями.