Об'ємна щільність енергії електричного поля
14.1. Енергія системи точкових зарядів
Мал. 14.1
Зі зіставлення (14.1) і (14.2) видно, що Q 1 Q 2 , тому енергію системи з двох точкових зарядів можна у симетричному вигляді:
де i– потенціал поля, створюваного всіма зарядами, крім i-го, у точці, де розташований i-ий заряд.
^
14.2. Енергія зарядженого провідника
Заряд, розташований лежить на поверхні провідника, можна як систему точкових зарядів, для обчислення енергії зарядженого провідника можна скористатися формулою (14.4). Потенціал будь-якої точки поверхні провідника однаковий ( i=), оскільки його поверхня еквіпотенційна. Отже, у формулі (14.4) потенціал можна винести за знак суми:
 або
або  , (14.5) де
, (14.5) де 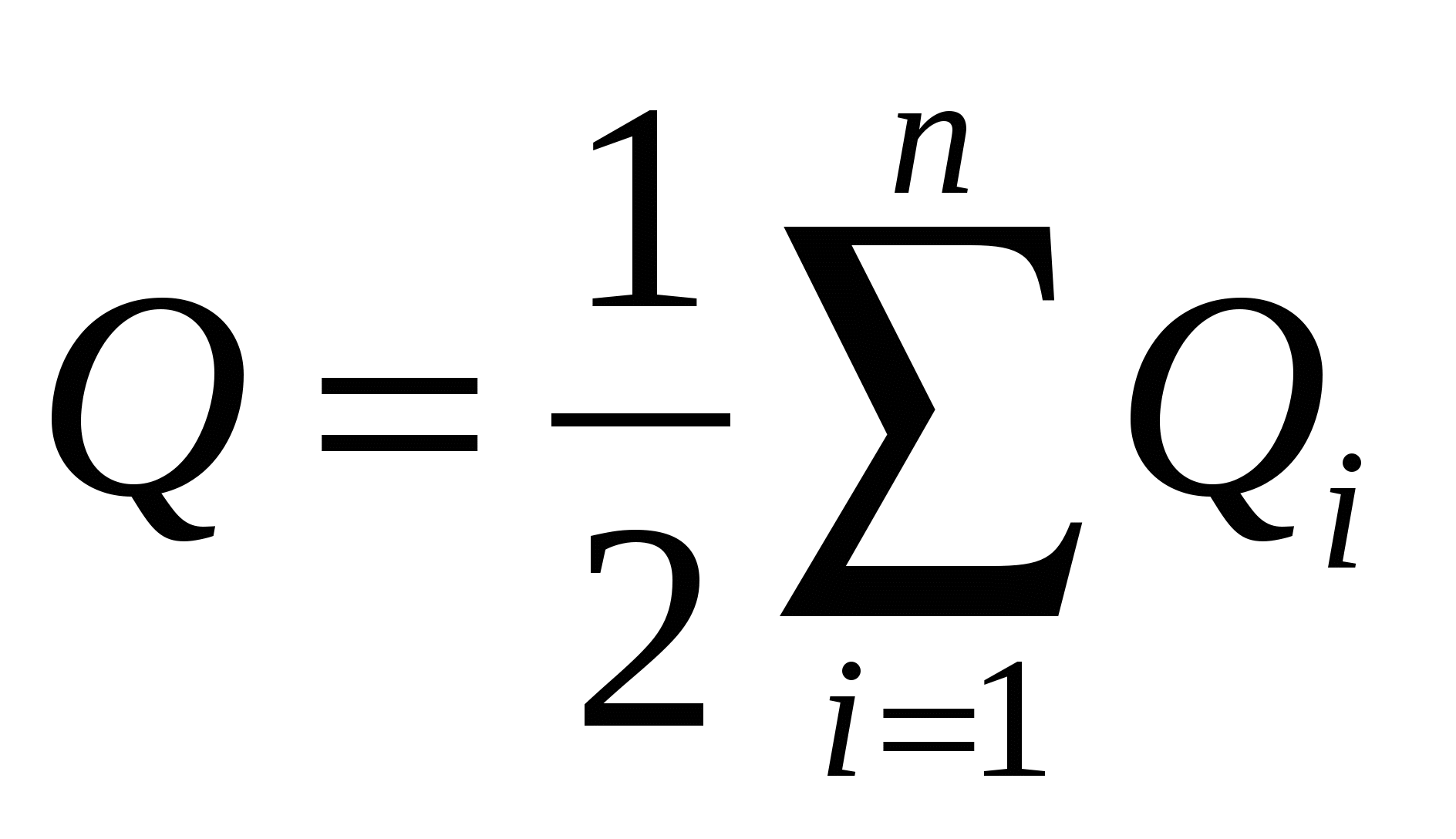 - Заряд провідника.
- Заряд провідника.
З урахуванням (13.3) вираз для енергії зарядженого провідника можна подати у вигляді
^
14.3. Енергія зарядженого конденсатора. Щільність енергії електростатичного поля
Для обчислення енергії зарядженого конденсатора скористаємося формулами (14.5) – (14.7), замінивши на різницю потенціалів між обкладинками конденсатора U= . Тоді
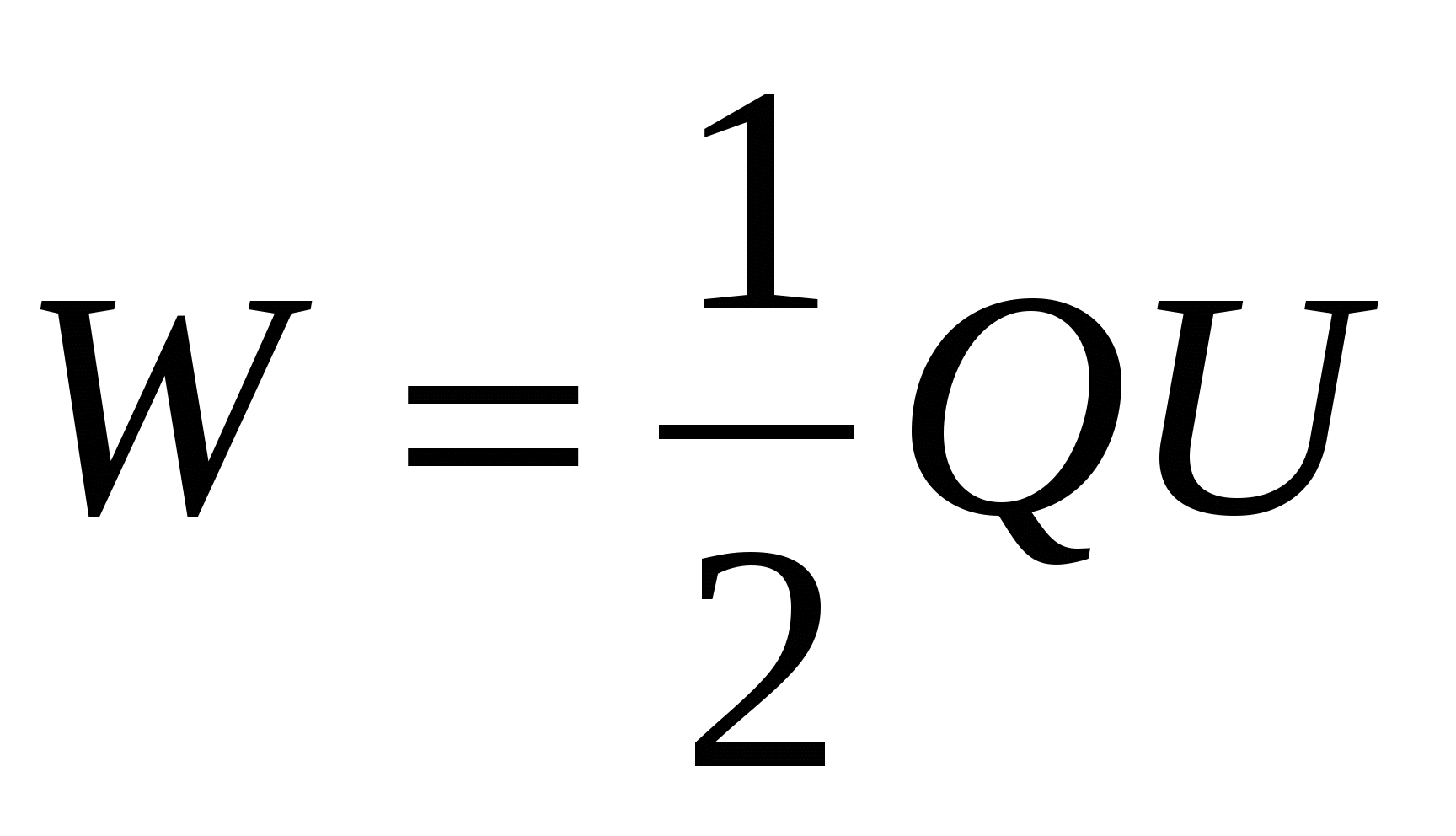 , , | (14.8) |
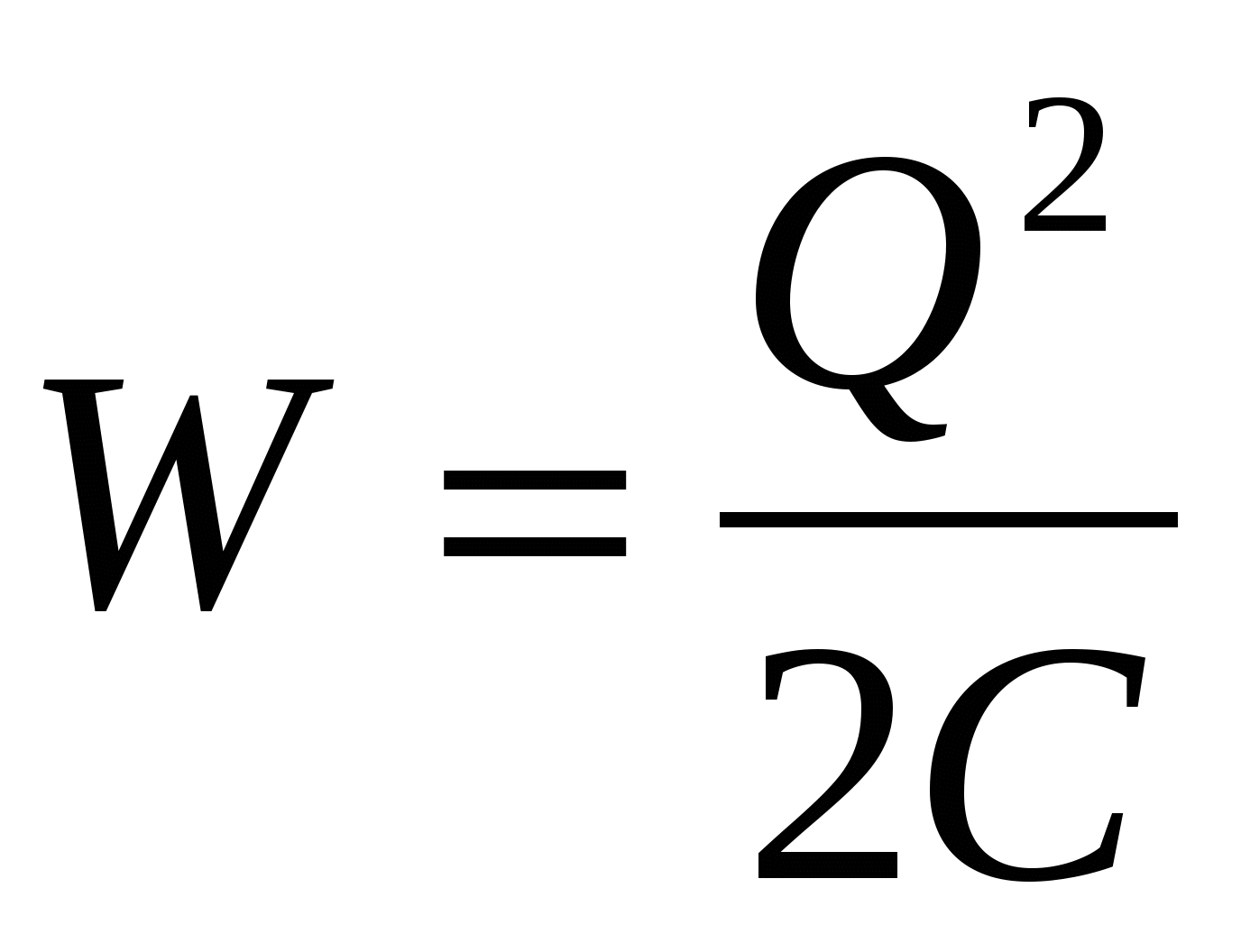 | (14.9) |
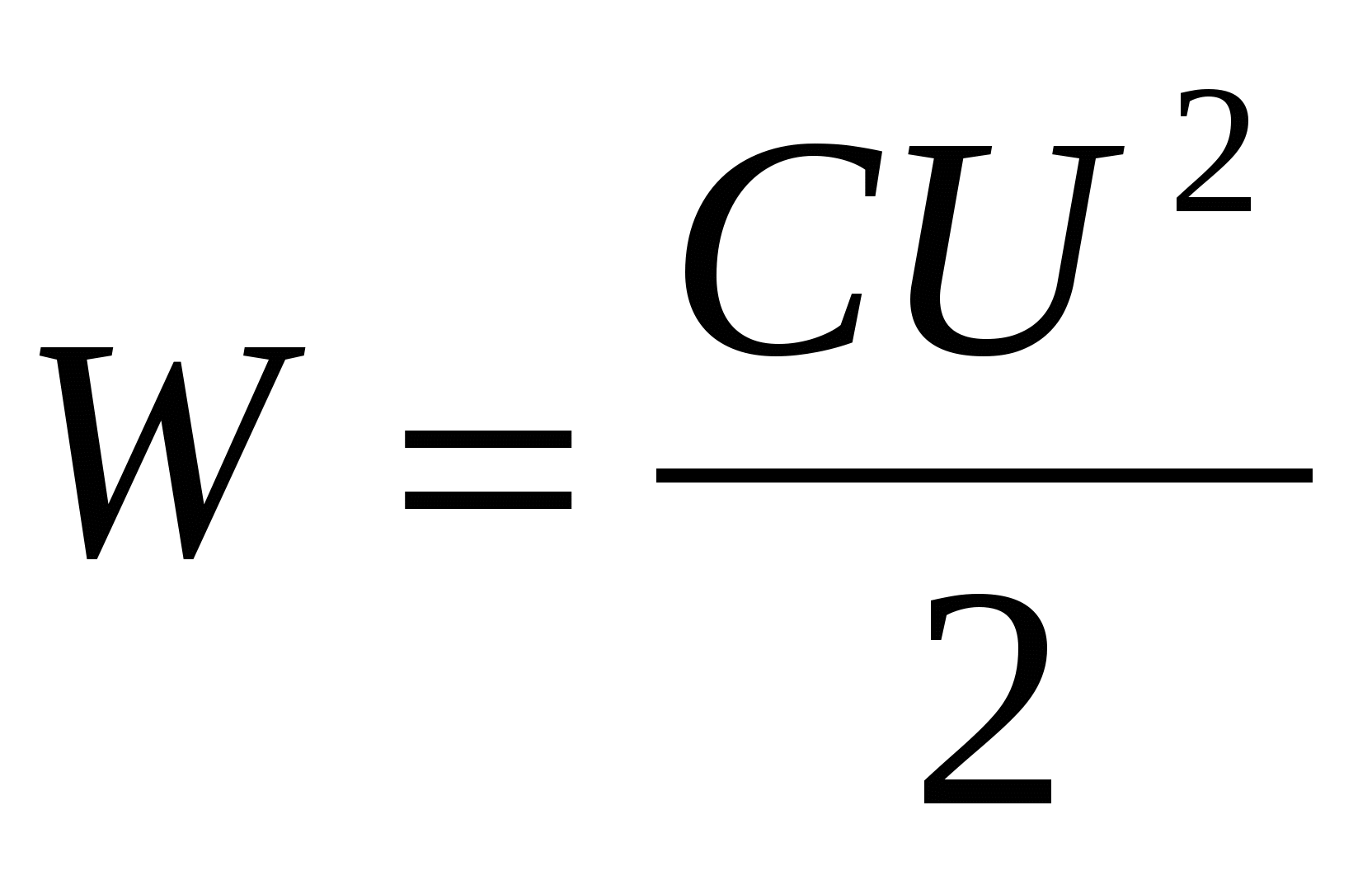 | (14.10) |
Подальший розгляд проведемо, ґрунтуючись на формулі (14.9). Представимо заряд конденсатора як Q= S, де – поверхнева щільність заряду, а S- Площа обкладення конденсатора. Скориставшись далі виразом для ємності плоского конденсатора (13.7), представимо (14.9) у вигляді
У формулі (14.9) енергія зарядженого конденсатора виражена через заряд на його обкладках та ємність. У формулі (14.12) енергія конденсатора виражена через напруженість електростатичного поля, зосередженого між його обкладинками. У зв'язку з цим виникає важливе питання про те, що є носієм енергії конденсатора: заряди або електростатичне поле. Це питання – центральне у тривалій дискусії між прихильниками далекодії та близькодії.
Прихильники далекодії віддавали перевагу формулі (14.9), розглядаючи її як потенційну енергію взаємодії двох тіл. Прихильники цієї теорії відкидали можливість здійснення взаємодії у вигляді поля.
Прихильники теорії близькодії (польової теорії) вважали, що енергія конденсатора є енергія електростатичного поля (формула (14.2)). Ця енергія "розмазана" по всьому обсягу конденсатора і, отже, можна говорити про об'ємну щільність енергії:
 [Дж/м 3 ] або
[Дж/м 3 ] або 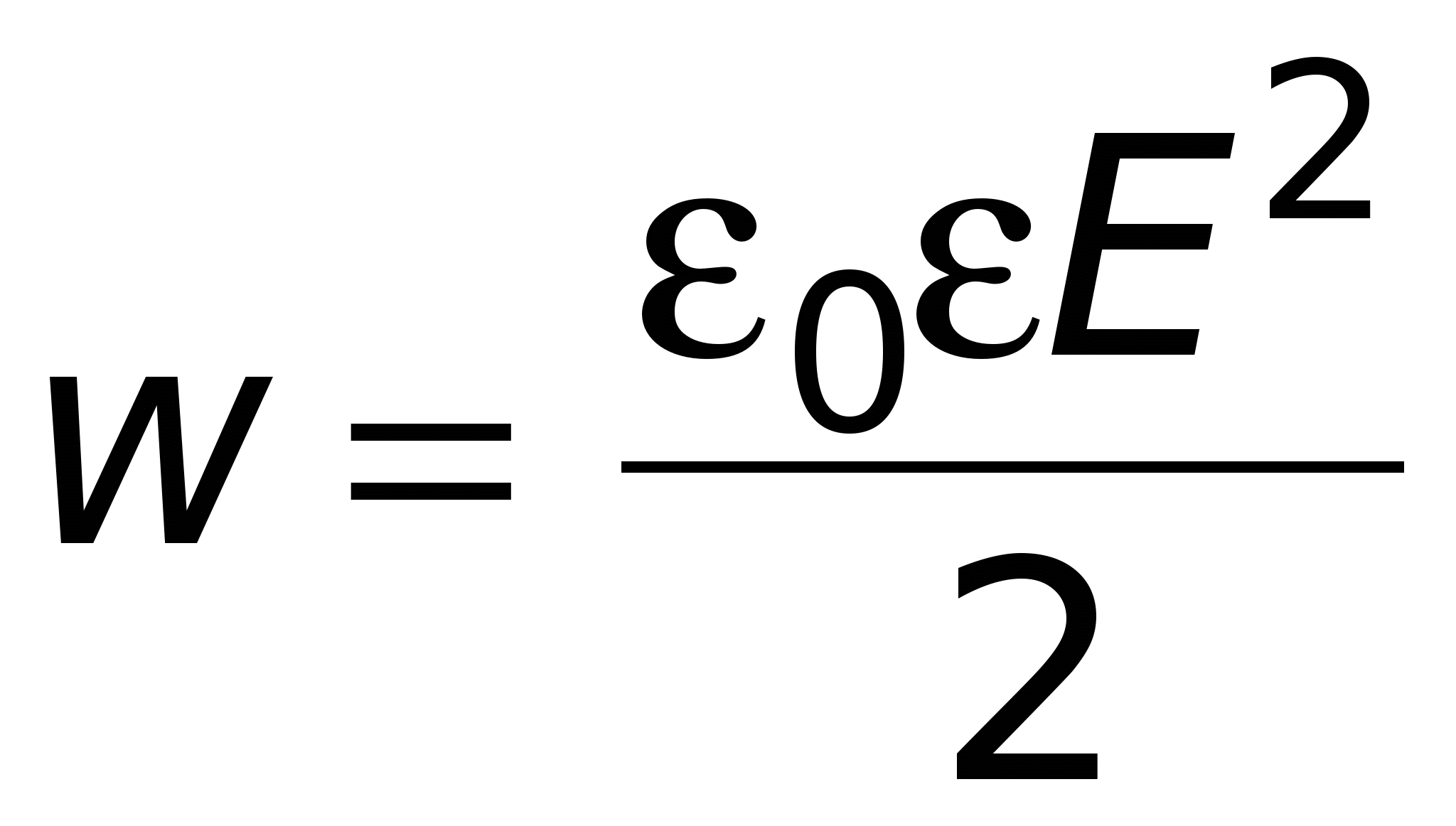 , З урахуванням (12.11) формулу (14.13) можна подати у вигляді
, З урахуванням (12.11) формулу (14.13) можна подати у вигляді
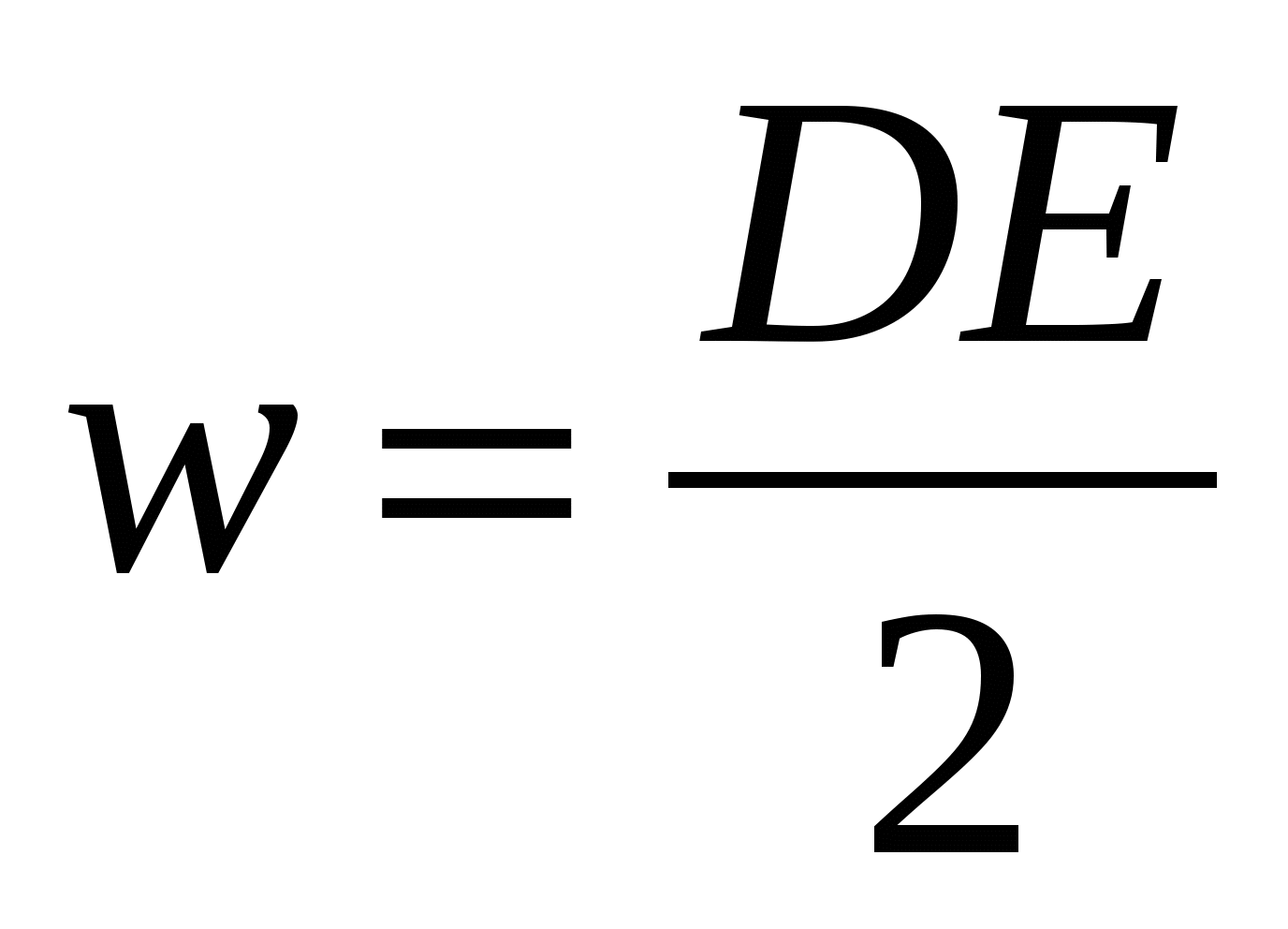 | (14.14) |
В рамках електростатики вирішити питання, що є носієм енергії – заряди або поле, неможливо, оскільки нерухомі заряди та електростатичне поле, що ними твориться, невіддільні один від одного. При вивченні змінних електричних та магнітних полів виявилося, що електромагнітне поле може відриватися від зарядів, існуючи незалежно від них. Це і є вирішальний аргумент на користь теорії близькодії (польової теорії).
лекція 23.
15. Постійний електричний струм
^
15.1. Сила та щільність струму
Електричним струмом називають упорядкований (спрямований) рух заряджених мікрочастинок або заряджених макроскопічних тіл. За напрям струму приймають напрямок руху позитивних зарядів; якщо струм створюється негативно зарядженими частинками (наприклад, електронами), то напрям струму протилежний напрямку руху частинок. Розрізняють струм провідності (спрямований рух заряджених частинок усередині макроскопічного тіла) та конвекційний (рух зарядженого тіла як цілого). Надалі розглядатимемо лише струм провідності.
Кількісно електричний струм характеризується скалярною величиною силою струму Iта векторною величиною – щільністю електричного струму  .
.
Сила струму чисельно дорівнює заряду, що пройшов через поперечний переріз провідника за одиницю часу:
де знак "" означає, що майданчик 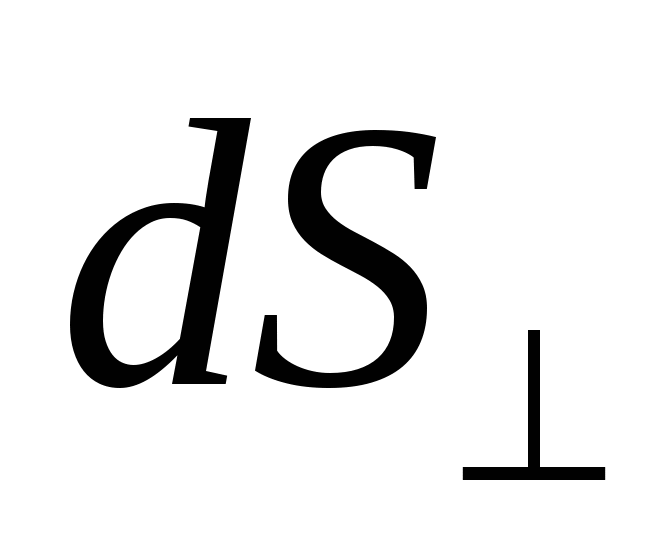 орієнтована перпендикулярно напрямку струму. Напрямок вектора збігається із напрямом руху позитивних зарядів.
орієнтована перпендикулярно напрямку струму. Напрямок вектора збігається із напрямом руху позитивних зарядів.
Знайдемо вираз для вектора густини струму в металах, у яких носіями струму є вільні електрони. Під дією електричного поляелектрони в металі рухаються спрямовано із середньою швидкістю 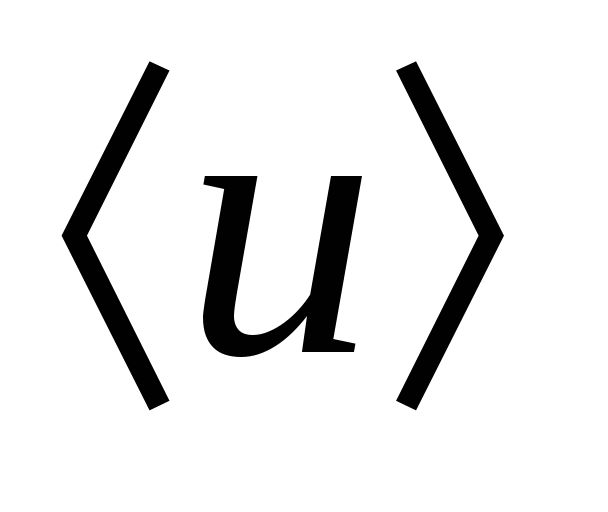 . За одиницю часу через одиничний майданчик поперечного перерізу провідника пройде nелектронів, де n- Число електронів в одиниці обсягу (концентрація). При цьому буде перенесено заряд en. Отже щільність струму
. За одиницю часу через одиничний майданчик поперечного перерізу провідника пройде nелектронів, де n- Число електронів в одиниці обсягу (концентрація). При цьому буде перенесено заряд en. Отже щільність струму
 . . | (15.3) |
15.2. Умови існування струму. Сторонні сили. ЕРС
Якщо вектор щільності струму не змінюється з часом ні за величиною, ні за напрямом, такий струм називається постійним. Знайдемо умови існування постійного струму.

Мал. 15.1
Припустимо, що на кінцях провідника створено різницю потенціалів  , причому
, причому 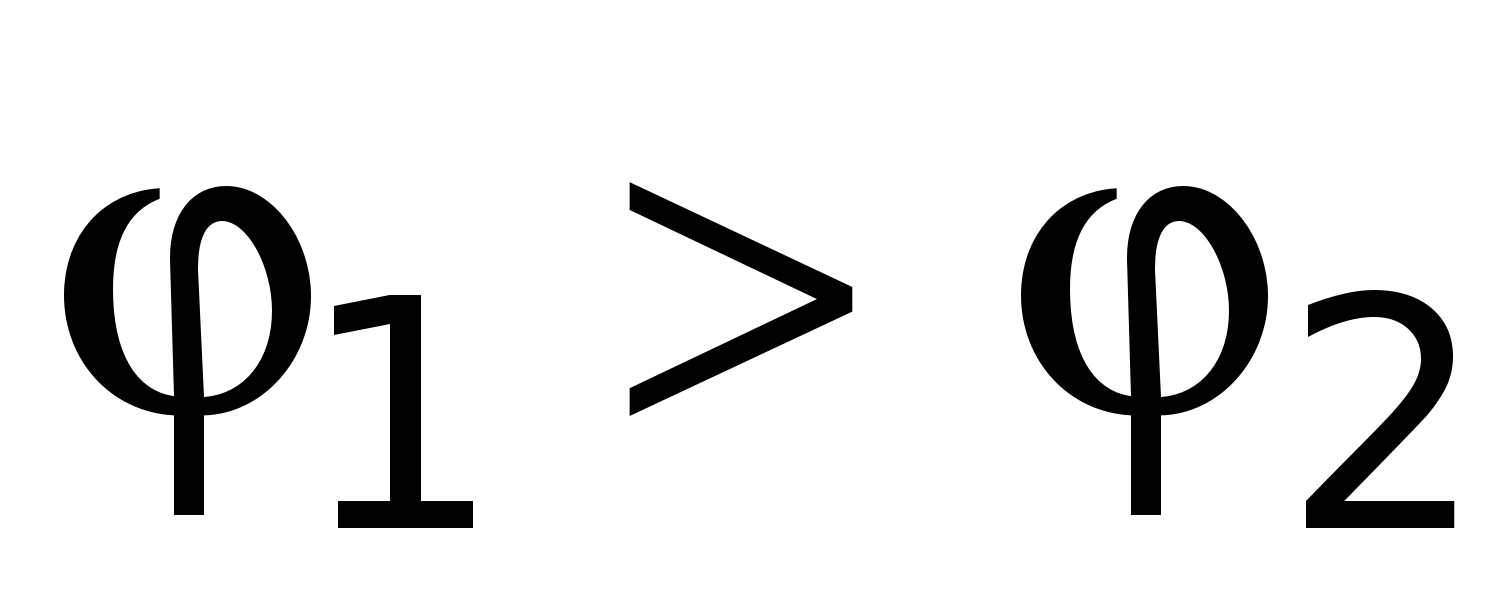 (Рис. 15.1). При цьому у провіднику виникне короткочасний струм, викликаний упорядкованим рухом зарядів у бік убутку потенціалу (передбачається, що носії струму мають позитивний заряд). Струм буде існувати до тих пір, поки не відбудеться вирівнювання потенціалів на кінцях провідника, Для того щоб струм зберігався постійним протягом тривалого часу, необхідно від кінця провідника з меншим потенціалом відводити заряди до кінця провідника з великим потенціалом, тобто. здійснювати кругообіг зарядів. У зв'язку з цим ланцюг повинен бути замкнутим.
(Рис. 15.1). При цьому у провіднику виникне короткочасний струм, викликаний упорядкованим рухом зарядів у бік убутку потенціалу (передбачається, що носії струму мають позитивний заряд). Струм буде існувати до тих пір, поки не відбудеться вирівнювання потенціалів на кінцях провідника, Для того щоб струм зберігався постійним протягом тривалого часу, необхідно від кінця провідника з меншим потенціалом відводити заряди до кінця провідника з великим потенціалом, тобто. здійснювати кругообіг зарядів. У зв'язку з цим ланцюг повинен бути замкнутим.
Електростатичні сили такий кругообіг зарядів забезпечити що неспроможні, оскільки дільниці ланцюга, показаному на рис. 15.1 пунктиром потрібно виконувати роботу проти електростатичного поля. Переміщення зарядів у бік зростання потенціалу можливе лише за допомогою додаткових сил неелектростатичного походження, які називаються сторонніми силами. Ці сили можуть бути забезпечені хімічними процесами (гальванічні елементи), електричним вихровим полем (генератори змінного або постійного струму) і т.д.
На відміну від електростатичних сил, робота сторонніх сил переміщення заряду по замкнутому колу відмінна від нуля. Електрорушійною силою(ЕРС) називається робота, що здійснюється сторонніми силами по переміщенню одиничного позитивного заряду по всьому ланцюгу, 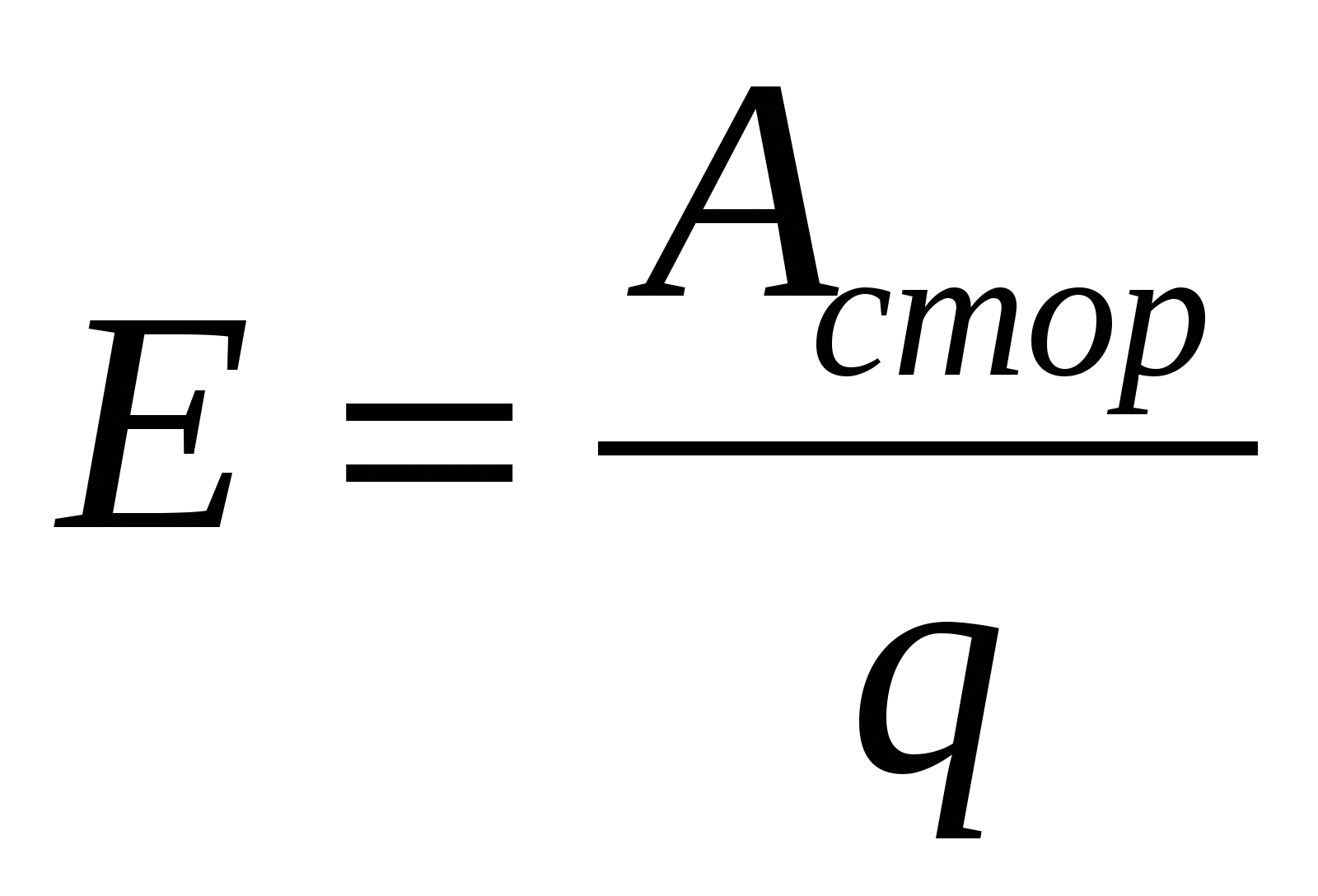 , (15.4). Як і різницю потенціалів, ЕРС вимірюється у вольтах.
, (15.4). Як і різницю потенціалів, ЕРС вимірюється у вольтах.
Розглянемо ділянку ланцюга, де крім сторонніх сил діють електростатичні. Тоді робота з переміщення заряду на цій ділянці дорівнюватиме сумі робіт: 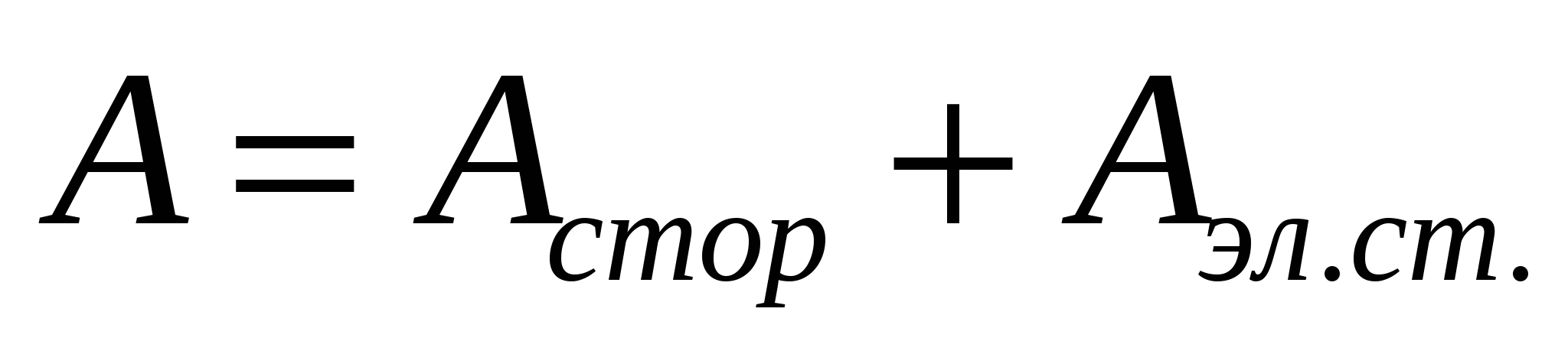
Розділимо цей вираз на заряд q:
Сумарна робота, що виконується як сторонніми, так і електростатичними силами щодо переміщення одиничного позитивного заряду на деякій ділянці ланцюга, називається напругою або падінням напруги:
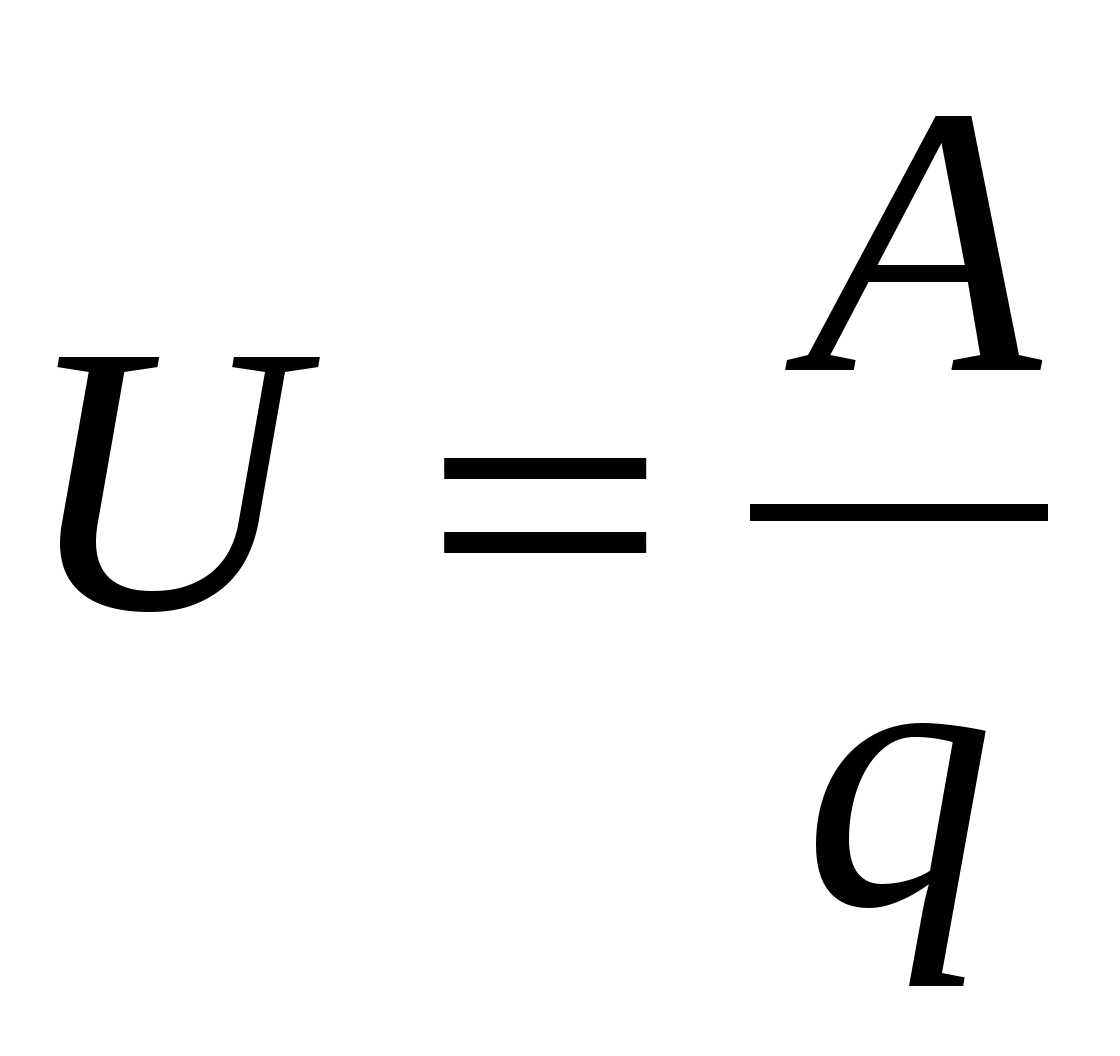 . . | (15.7) |
Підставивши (15.4), (15.6) і (15.7) в (15.5), отримаємо зв'язок між напругою, ЕРС та різницею потенціалів U = E + ( 1 - 2 )
З (15.8) видно, що напруга Uдорівнює алгебраїчній сумі ЕРС та різниці потенціалів на даній ділянці ланцюга.
^
15.3. Закон Ома
15.3.1. Закон Ома для неоднорідної ділянки ланцюга
Ом експериментально встановив, що сила струму на деякій ділянці ланцюга пропорційна напрузі і обернено пропорційна опору: 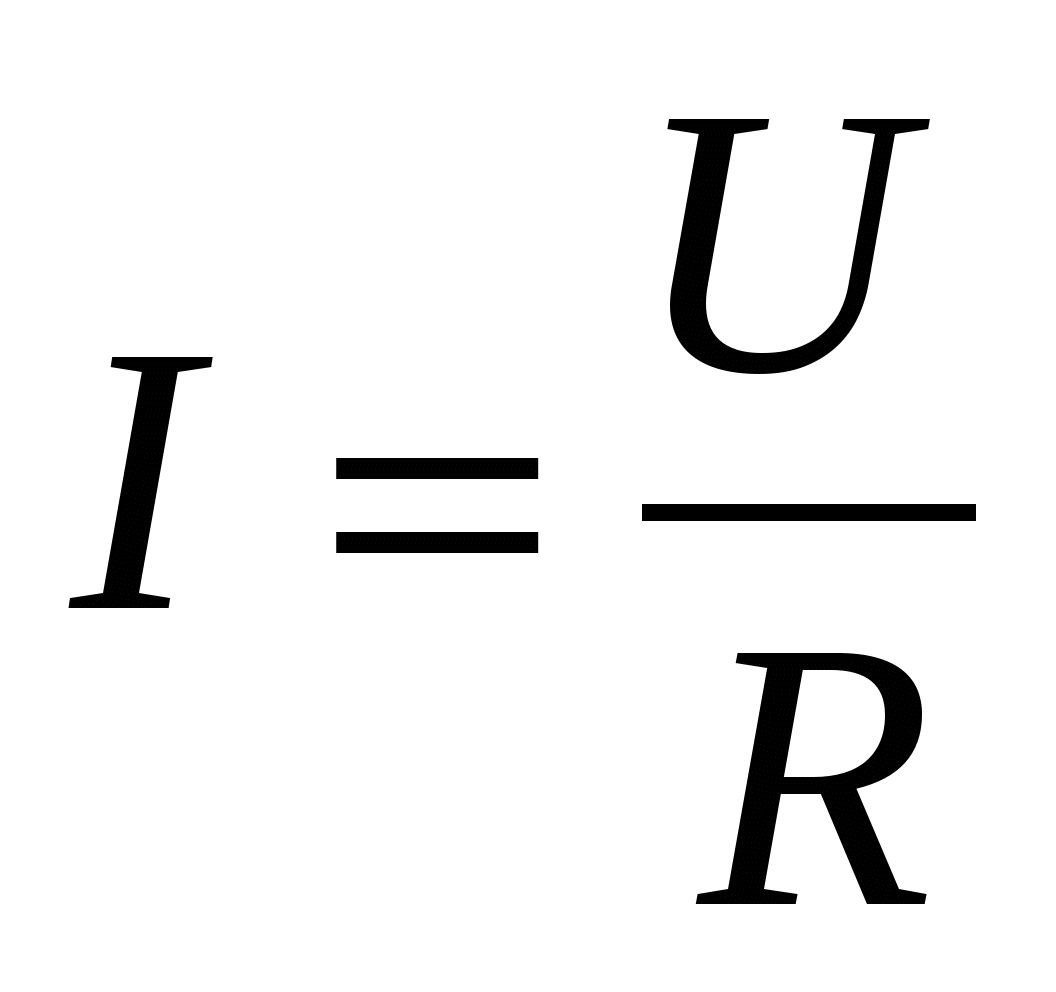 . . | (15.9) |
Знайдемо з (15.9) напруга Uі підставимо (15.8): IR= E +( 1 – 2 ) , (15.10)
Отримане є Закон Ома для неоднорідного ділянки ланцюга, тобто. ділянки ланцюга, що містить ЕРС.

Мал. 15.2
При практичному використанніформули (15.10) потрібно встановити знаки для напруги та ЕРС. Для цього довільним чином встановлюємо напрямок обходу (на рис. 15.2 напрямок обходу вибрано за годинниковою стрілкою). Якщо напрям струму збігається з напрямом обходу, він береться зі знаком " + " , інакше його треба взяти зі знаком " - " . На рис. 15.2 напрям обходу та напрям струму не збігаються, тому у формулі (15.10) IRберемо зі знаком "мінус".
Решта замкнутого контуру на рис. 15.2 показано пунктиром. ЕРС з зовнішнього ланцюга"переганяє" заряди від свого "плюсу" до "мінуса". Її потрібно брати зі знаком "+", якщо вона діє у напрямку обходу та зі знаком "-" в іншому випадку. Відповідно до цього на схемі, зображеній на рис. 15.2 ЕРС потрібно взяти зі знаком "+". Таким чином, закон Ома для неоднорідної ділянки ланцюга в даному випадку запишемо у вигляді: –
IR=
E
+(
1
–
2
)
.
^
15.3.2. Закон Ома для повного ланцюга
При обході повного ланцюгапочаткова та кінцева точки збігаються, тому 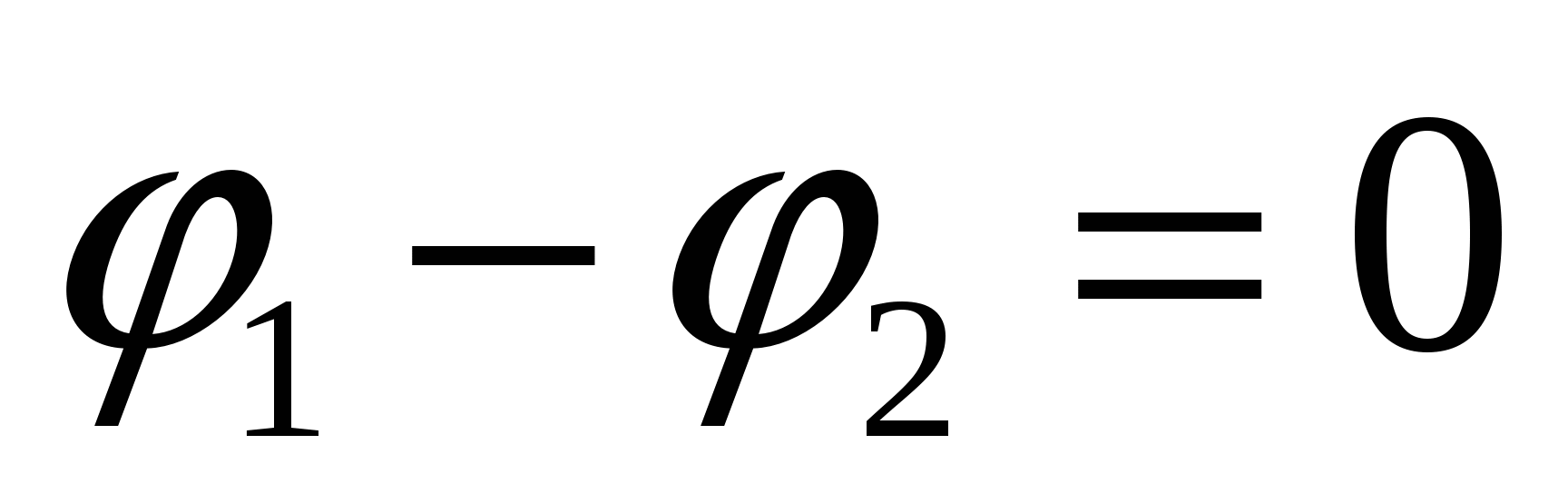 ;
;
^
15.3.3. Закон Ома для однорідної ділянки ланцюга
Однорідним називається ділянка ланцюга, яка містить джерела ЕРС, тобто. у формулі (15.10) потрібно покласти E
=0
. Тоді 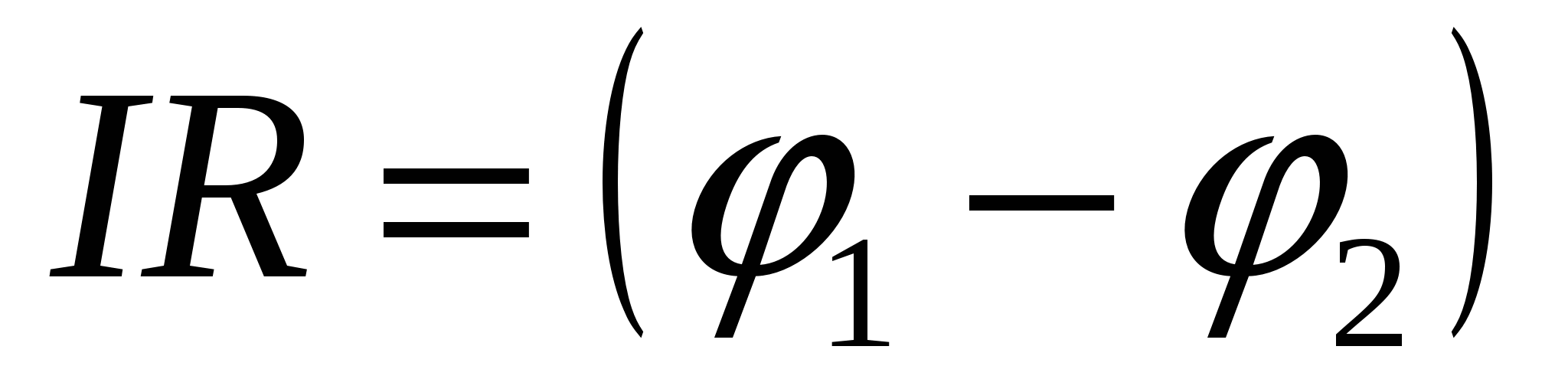 .
.
У разі падіння напруги збігається з різницею потенціалів U= 1 - 1, тобто.
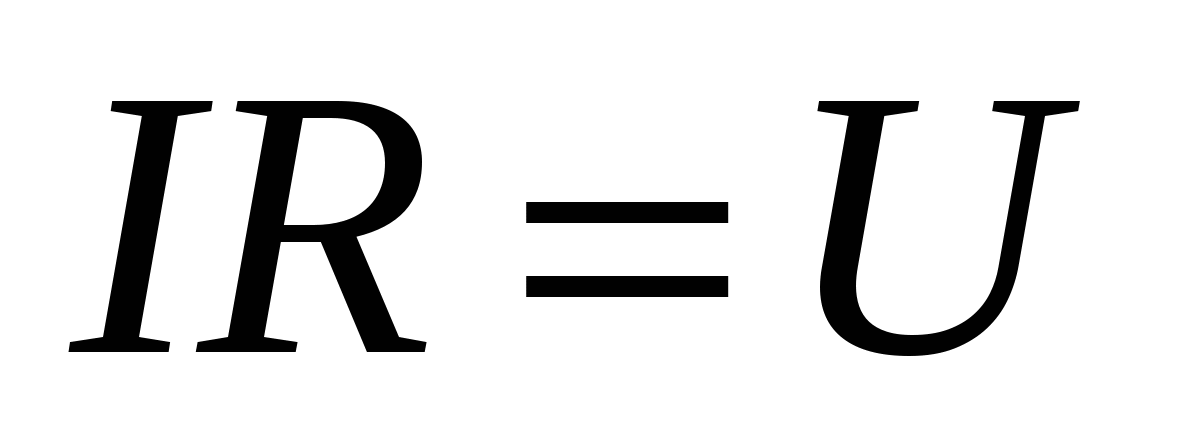 , , | (15.13) |
що також збігається з (15.9).
Формули (15.9) та (15.13) представляють закон Ома в інтегральній формі.
^
15.3.4. Закон Ома у диференційній формі
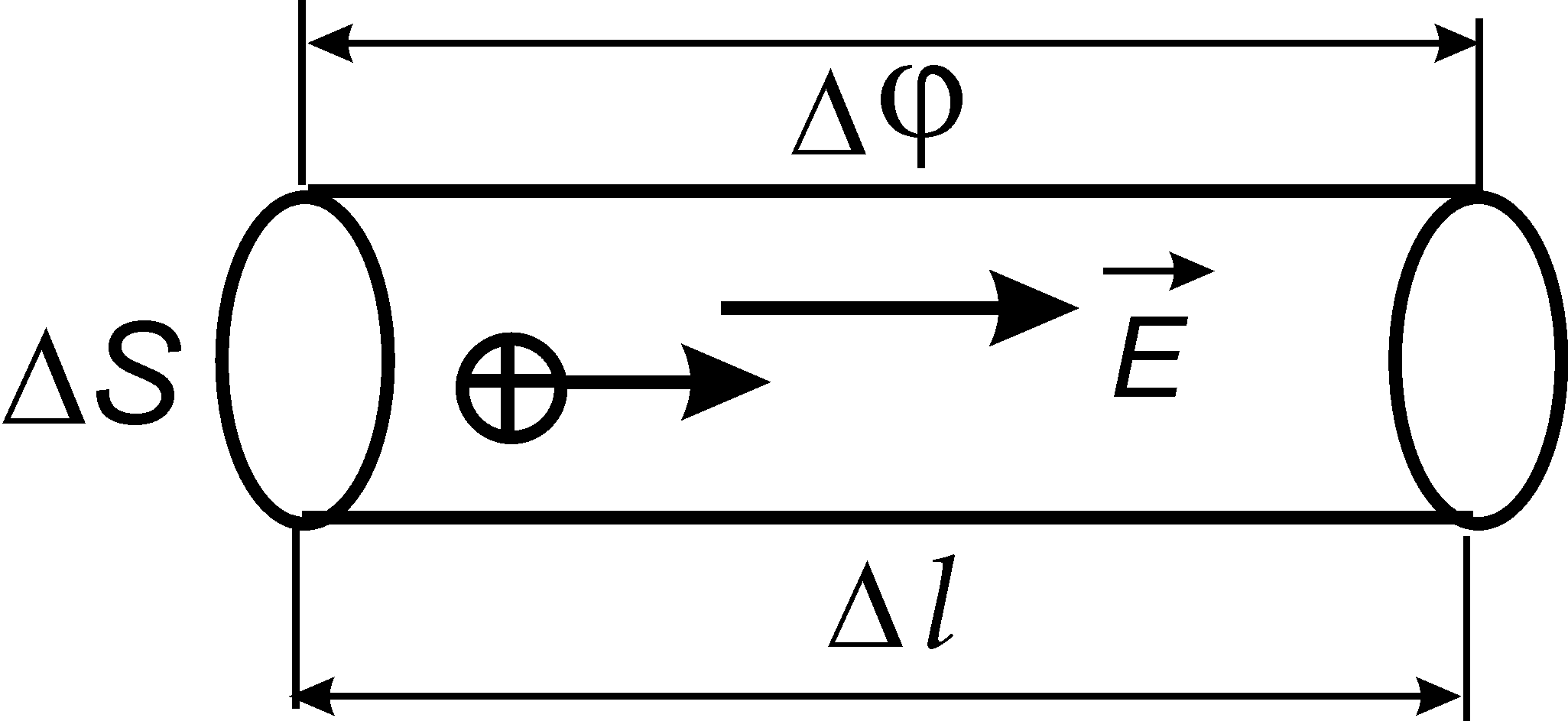
Мал. 5.3
Виділимо всередині провідника зі струмом елементарний циліндр перерізом Sта довжиною l(Рис. 15.3). Сила струму в ньому I=S, а його опір  , де – питомий опір провідника. Різниця потенціалів на кінцях циліндра . Тоді закон Ома (див. (15.9)) запишемо у вигляді
, де – питомий опір провідника. Різниця потенціалів на кінцях циліндра . Тоді закон Ома (див. (15.9)) запишемо у вигляді
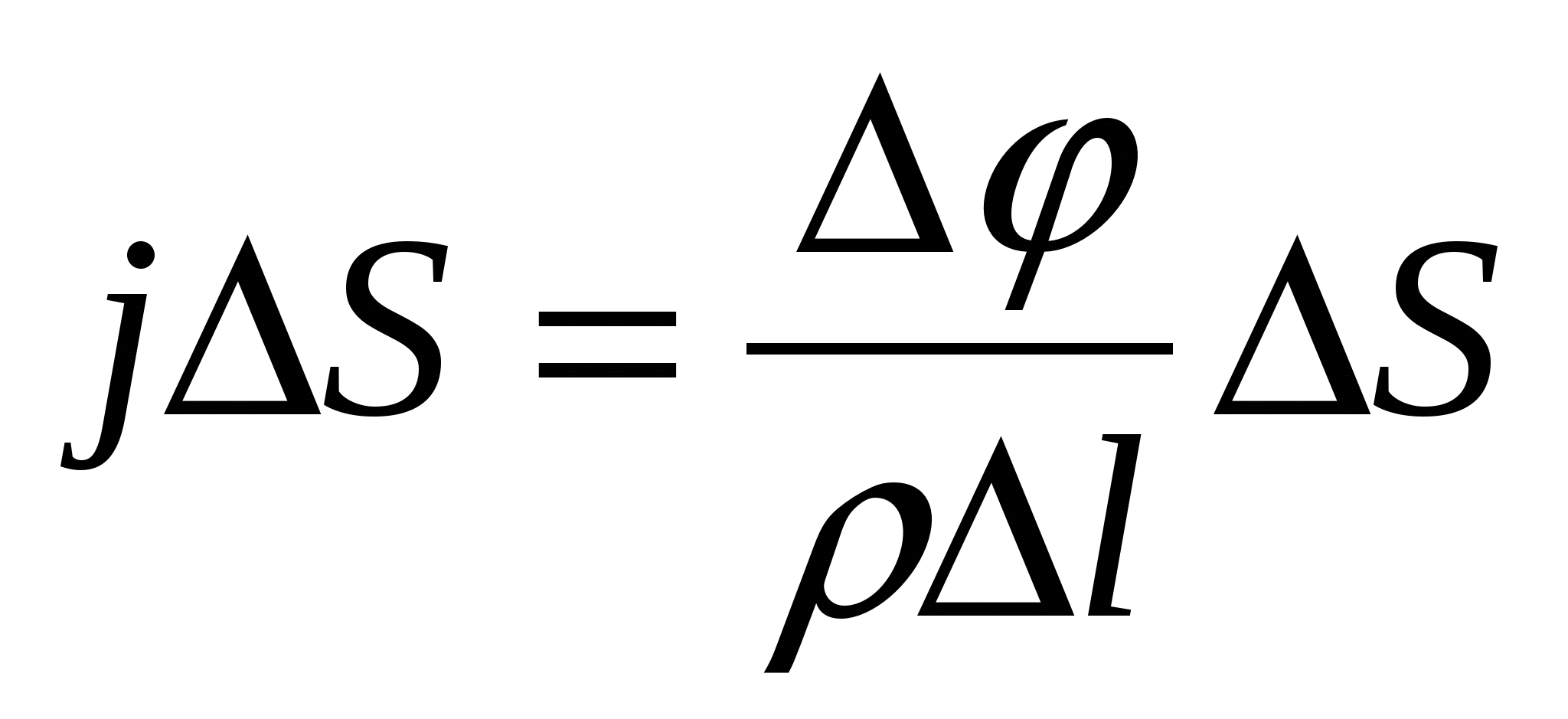 або .
або .
З урахуванням (11.30) останній вираз можна перетворити на вигляд
 . . | (15.14) |
Величина, зворотна питомому опору, називається питомою провідністю:
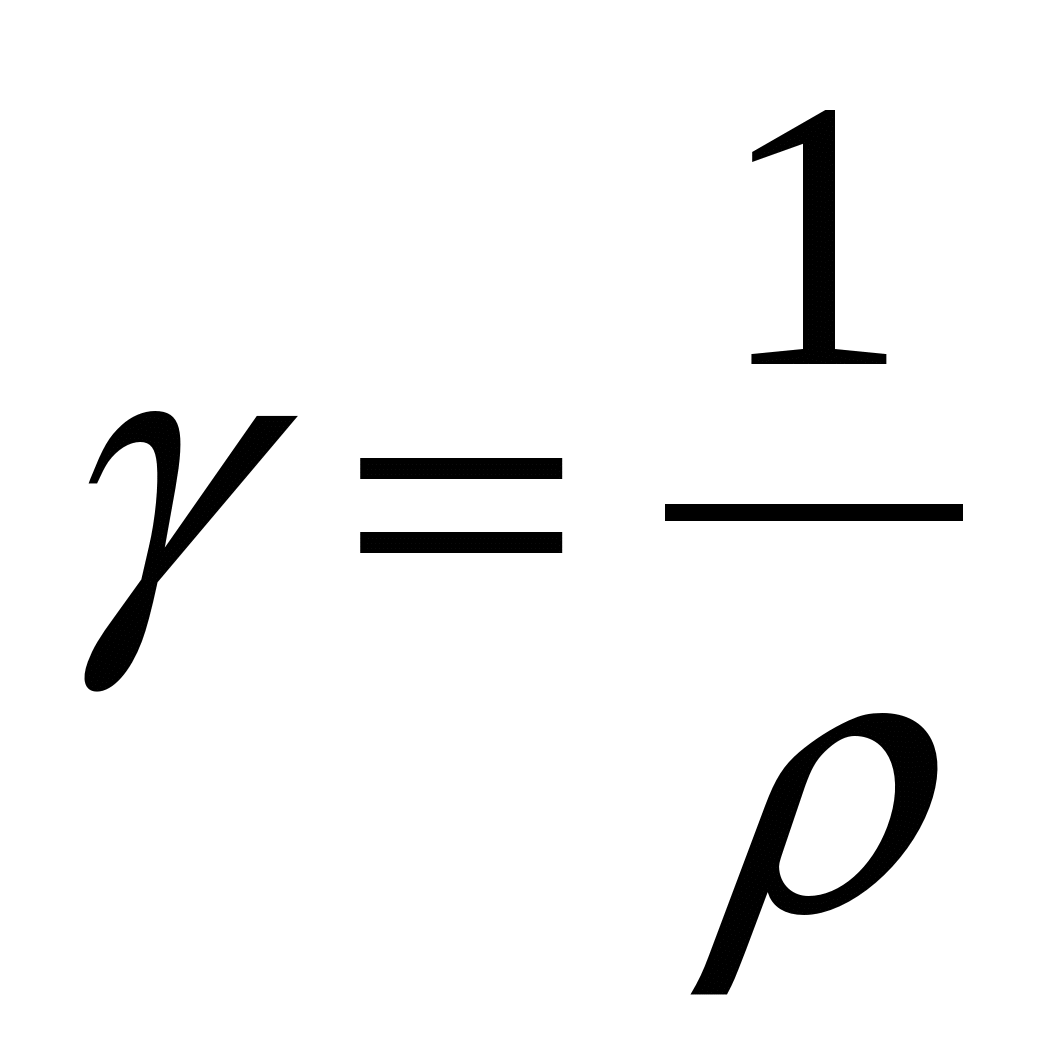 .
.Тоді закону Ома в диференційній формі (15.4) можна надати вигляду 
^
15.4. Закон Джоуля-Ленца
15.4.1. Закон Джоуля-Ленца в інтегральній формі
Джоуль і незалежно від нього Ленц експериментально встановили, що кількість теплоти, виділеної в провіднику опором Rза час dt, пропорційно квадрату сили струму, опору та часу: 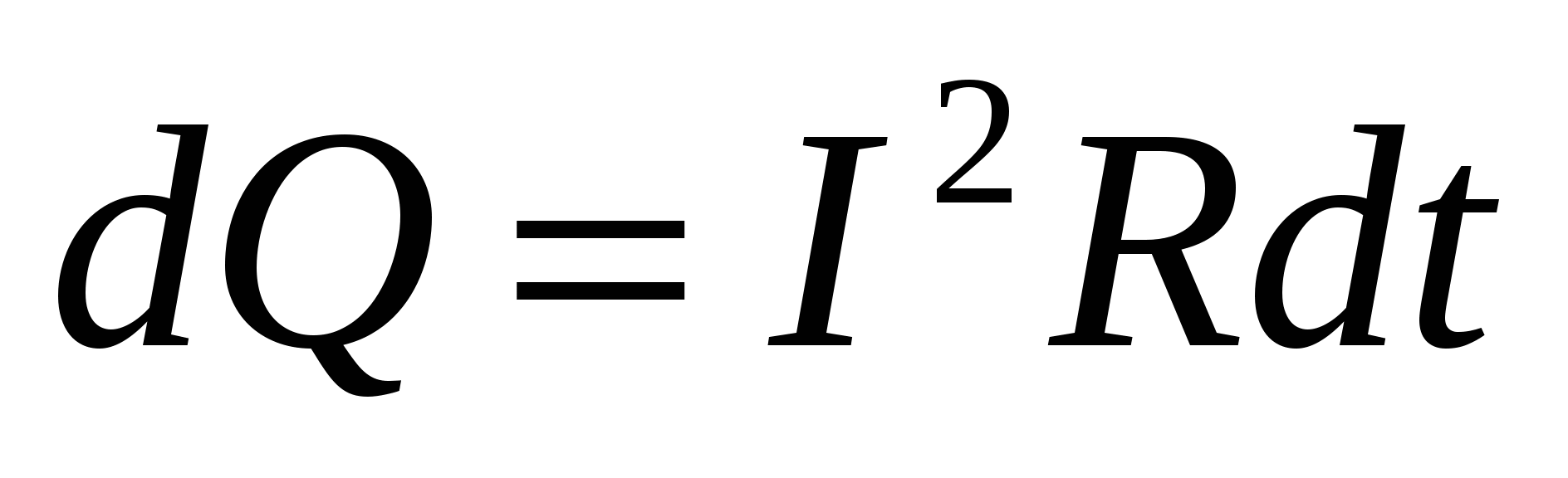 . . | (15.16) |
Формула (15.16) представляє закон Джоуля-Ленца в інтегральній формі.
^
15.4.2. Закон Джоуля-Ленца у диференційній формі
Виділимо, як і раніше, усередині провідника елементарний циліндричний об'єм (рис. 15.3). Замінимо в (15.16)
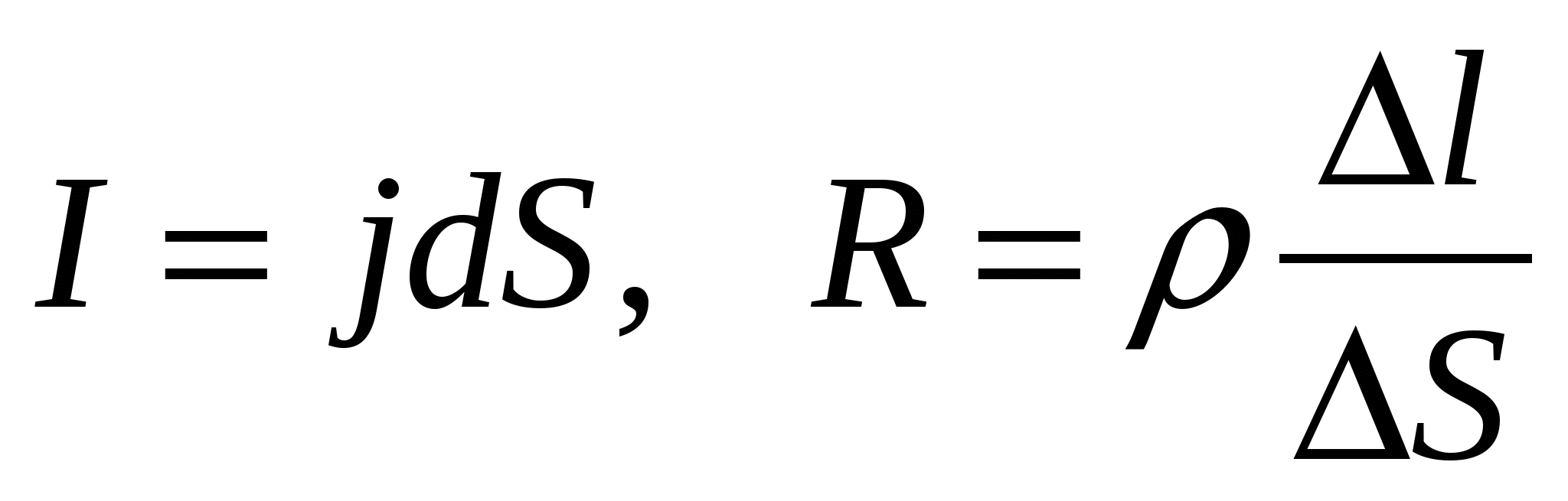 . Тоді
. Тоді  де V= lS- Об'єм провідника. Введемо на розгляд питому потужність теплоти
де V= lS- Об'єм провідника. Введемо на розгляд питому потужність теплоти 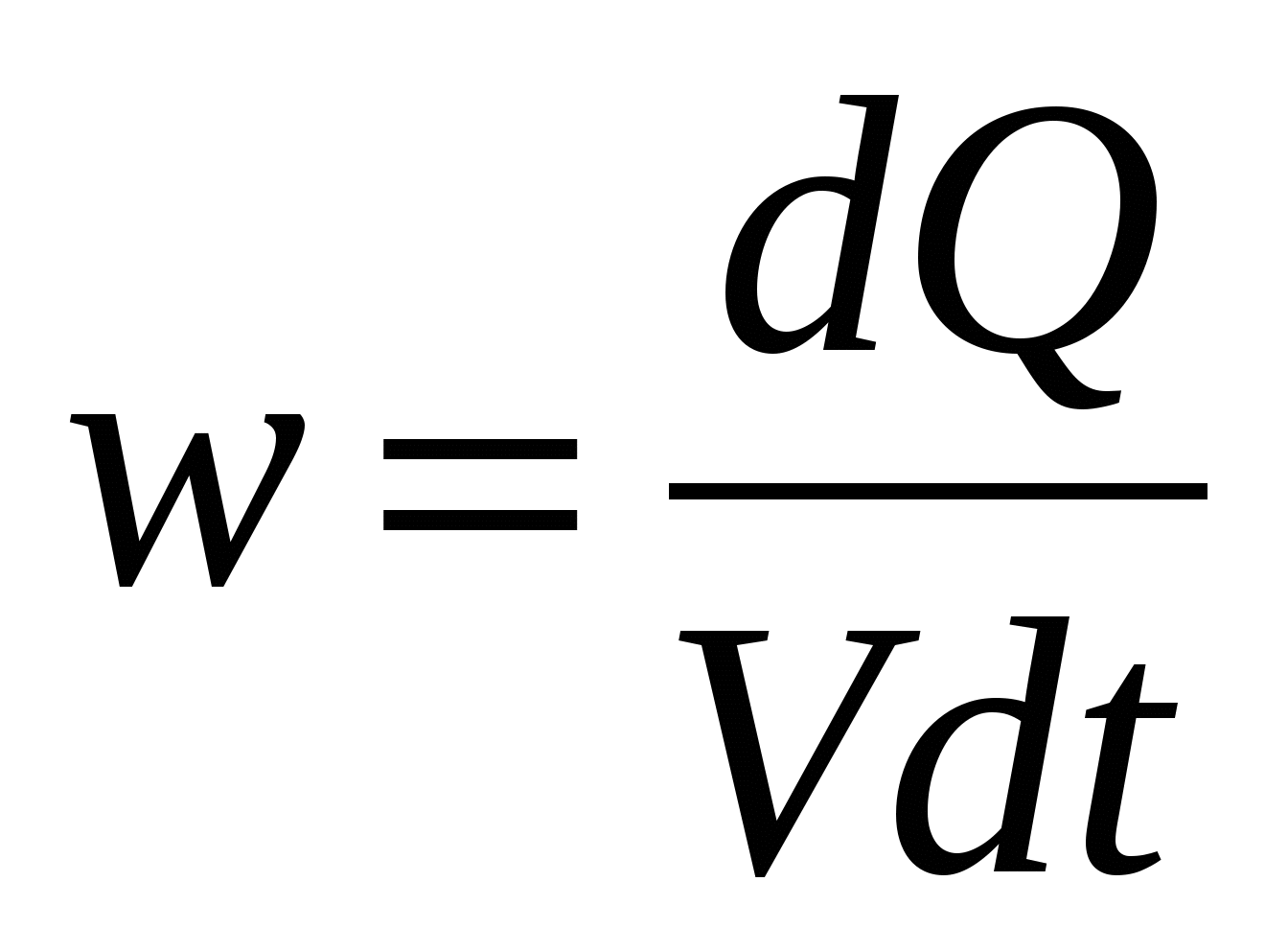 [Дж/м 3 с = Вт/м 3]. [Дж/м 3 с = Вт/м 3]. | (15.18) |
Питома потужність теплоти чисельно дорівнює кількості теплоти, виділеної одиниці обсягу провідника за одиницю часу. Іншими словами - це теплова потужність, що розвивається в одиниці обсягу. З урахуванням (15.18) виразу (15.17) можна надати вигляду
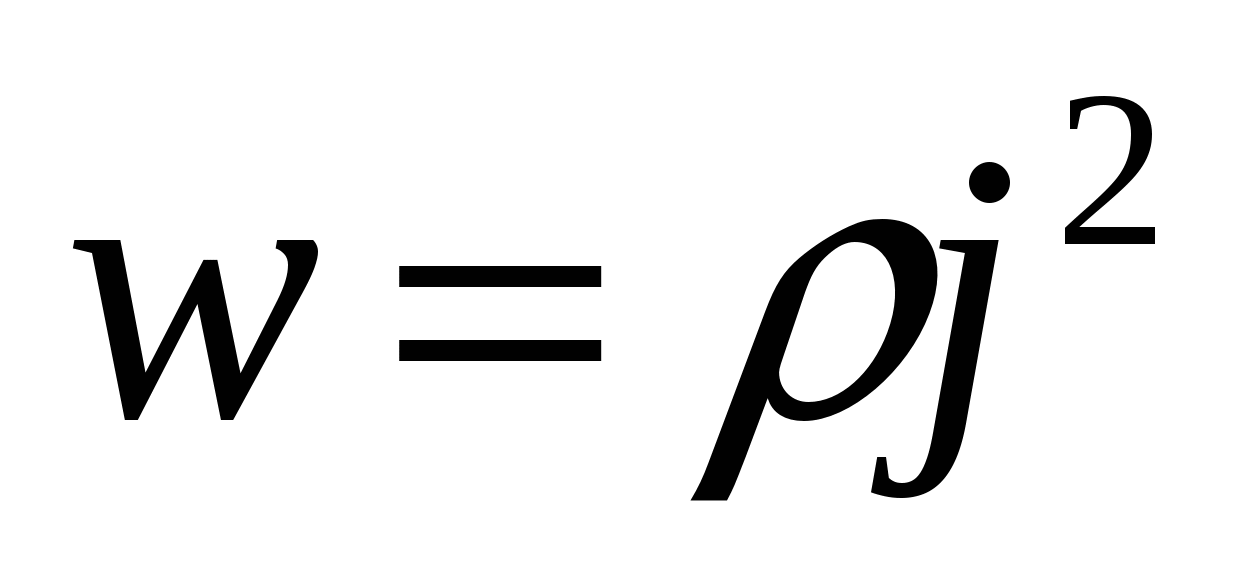 .
.
Формули (15.19) та (15.20) представляють закон Джоуля-Ленца у диференційній формі.
лекція 24.
^
15.5. Обґрунтування законів Ома та Джоуля-Ленца з класичної електронної теорії
У класичній електронної теоріїметалів приймається така модель.
1. Носіями струму у металах є вільні електрони.
2. Вільні електрони утворюють електронний газ, який за своїми властивостями аналогічний до ідеального газу. Є лише одна відмінність: електрони зі своїм рухом зіштовхуються між собою, і з іонами кристалічної решітки.
3. Під дією електричного поля електрони поряд із хаотичним рухом зі швидкістю  починають рухатися спрямовано зі швидкістю
починають рухатися спрямовано зі швидкістю  . При цьому швидкість спрямованого руху значно менша за швидкість хаотичного руху
. При цьому швидкість спрямованого руху значно менша за швидкість хаотичного руху
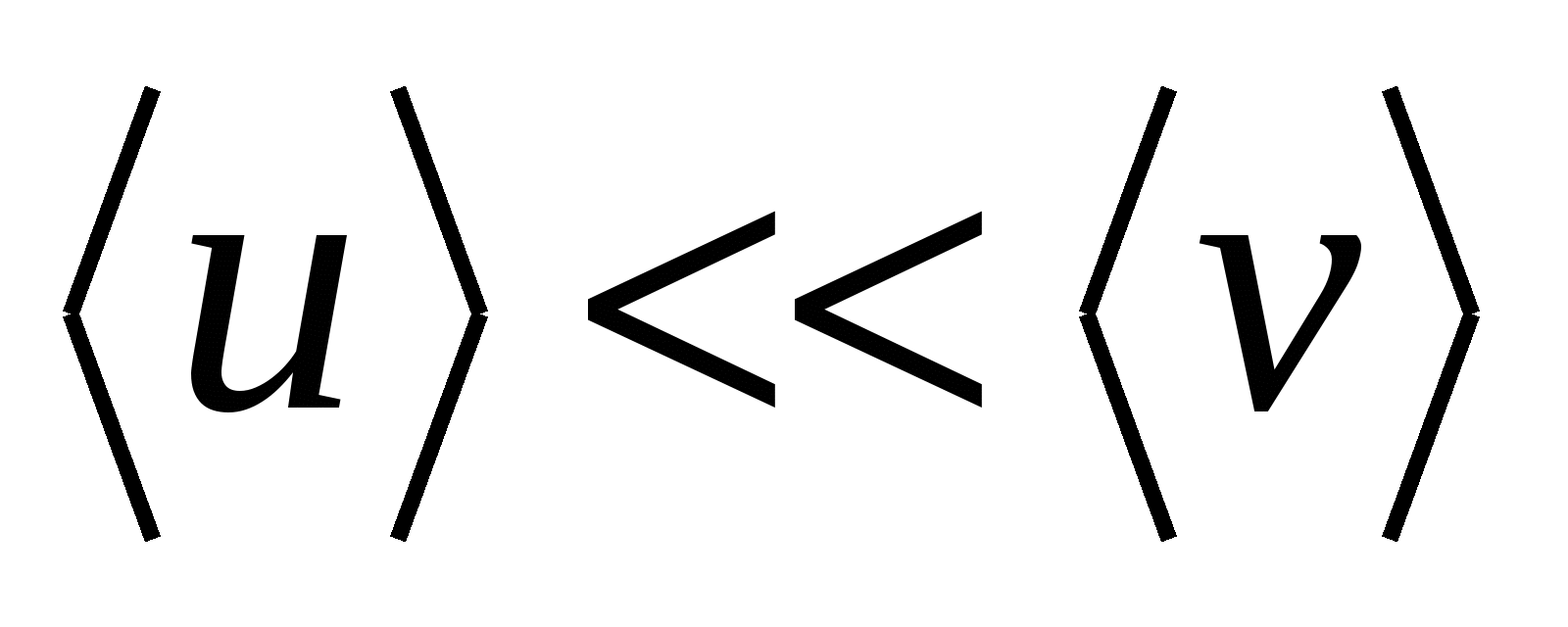 . . | (15.21) |
Знайдемо швидкість спрямованого руху електронів. Припустимо, що в момент часу t= 0 швидкість спрямованого руху електронів u 0 = 0. Під дією сили F=eEелектрон відповідно до другого закону Ньютона починає рухатися прискорено:
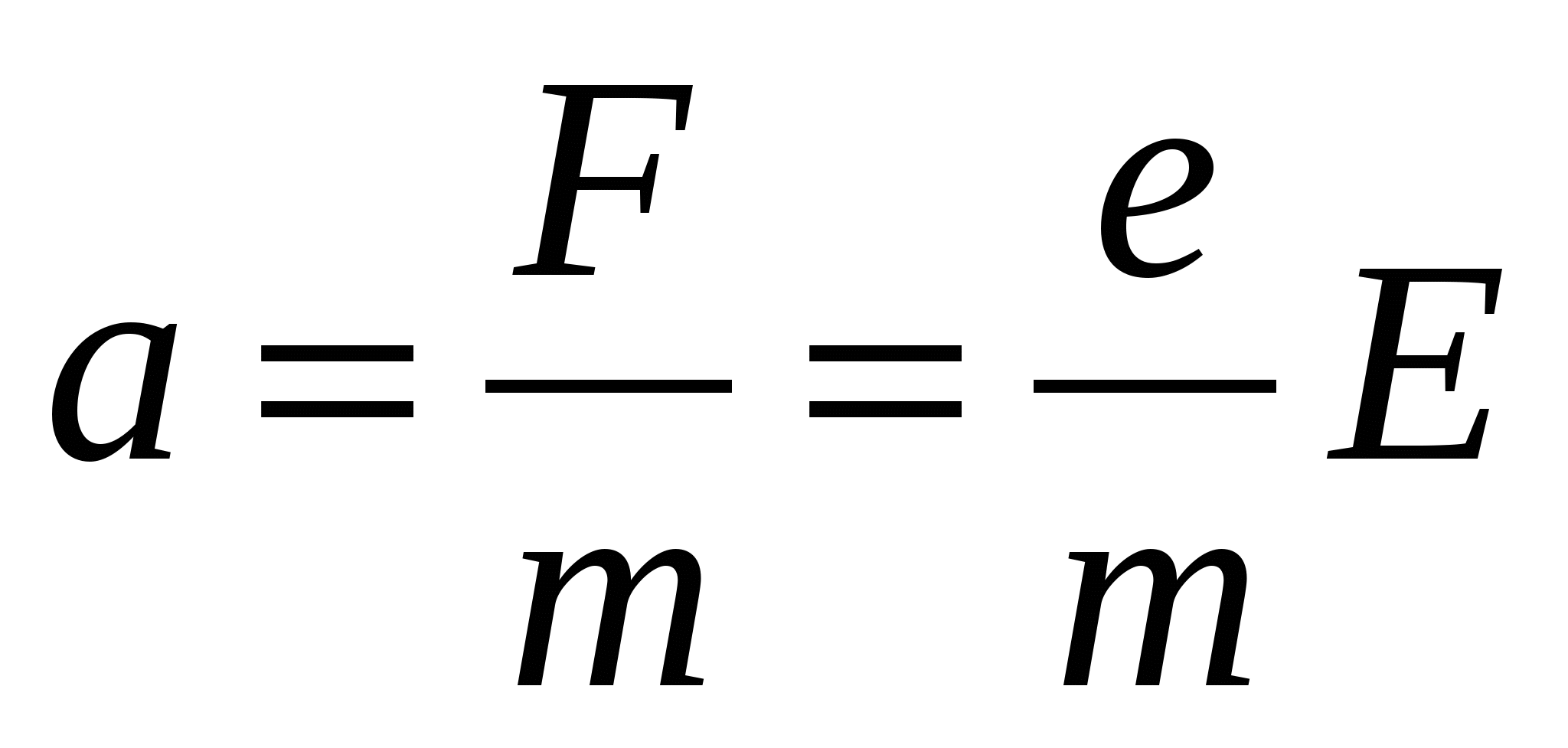 .
.
Швидкість спрямованого руху електрона
 . . | (15.22) |

Мал. 15.4
З формули (15.22) випливає, що швидкість електрона uз часом має зростати необмежено. Однак через деякий проміжок часу електрон відчуває зіткнення з іоном кристалічних ґрат і зупиняється. Схематично залежність швидкості спрямованого руху від часу зображено на рис. 15.4.
Середній час між двома послідовними зіткненнями електрона
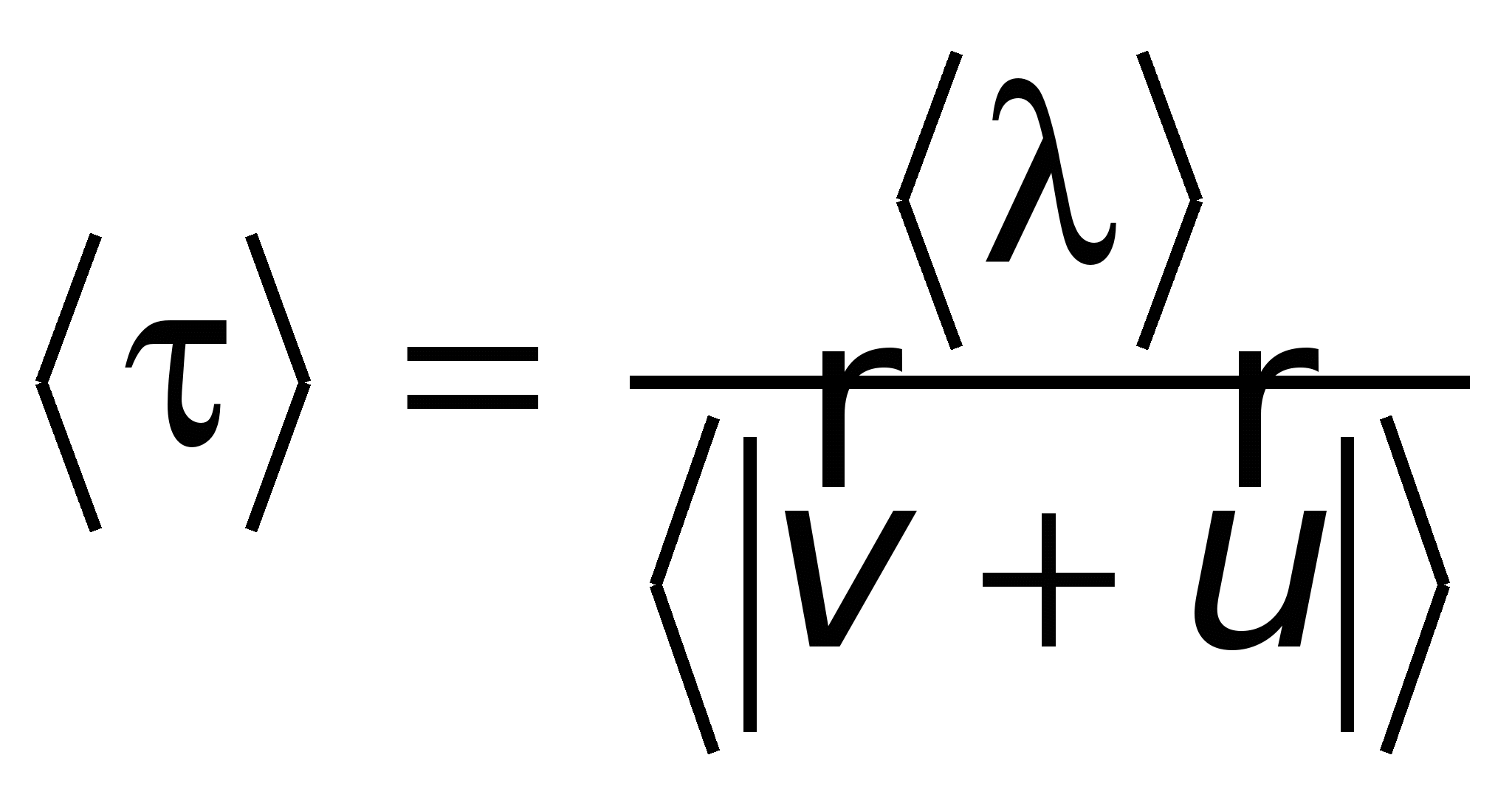 , , | (15.23) |
де
 - Середня довжина вільного пробігу електрона;
- Середня довжина вільного пробігу електрона;  - Середнє значення його швидкості, яка є векторною сумою швидкостей хаотичного та спрямованого рухів.
- Середнє значення його швидкості, яка є векторною сумою швидкостей хаотичного та спрямованого рухів. Через нерівність (15.21) швидкістю спрямованого руху можна знехтувати, тому
 . .
через характеристики електронного газу. Виходячи з уявлень класичної електронної теорії металів, отримаємо тепер закон Джоуля-Ленца. До кінця вільного пробігу електрон має кінетичну енергію спрямованого руху
Підставляючи сюди значення максимальної швидкості спрямованого руху електрона з (15.25) та враховуючи, що середня кількість зіткнень за 1 с
отримуємо закон Джоуля-Ленца
Зі зіставлення (15.30) і (15.20) знаходимо такий же вираз для питомої теплопровідності, Як і в законі Ома (див. (15.28)). Незважаючи на очевидні успіхи класичної електронної теорії металів, вона зіткнулася з низкою труднощів. Зокрема класична теорія неправильно передбачає залежність опору металу від температури. Аналіз виразу (15.29) показує, що від температури залежить лише швидкість хаотичного руху. При цьому (див. формулу (8.18)) Мал. 15.5 Перше правило Кірхгофа.Алгебраїчна сума струмів, які сходяться на вузлі, дорівнює нулю, тобто.
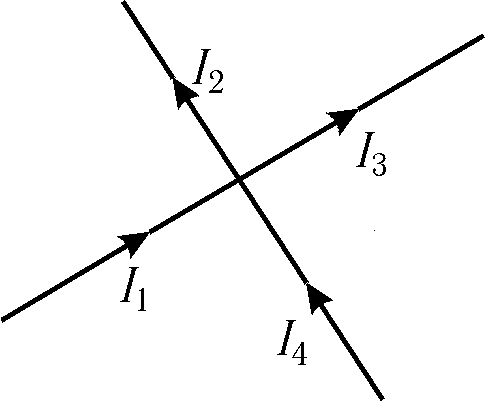
Вузлом називається точка ланцюга, де перетинаються три і більше провідників. Струм береться зі знаком "+", якщо він входить у вузол; струм, що виходить з вузла, береться зі знаком "-". Мал. 15.6 тобто. сума струмів, що входять у вузол, дорівнює сумі струмів, що виходять із нього. Перше правило Кірхгофа – наслідок закону збереження електричного заряду: заряди, потрапивши у вузол, нікуди не зникають і накопичуються. ^
Друге правило Кірхгофа.
Алгебраїчна сума падінь напруги в замкнутому контурі, виділеному зі складного ланцюга, дорівнює сумі алгебри ЕРС, включених в цей контур:
Падіння напруги береться зі знаком "+", якщо струм спрямований у бік обходу контуру, і "-" інакше. ЕРС береться зі знаком "+", якщо вона діє у напрямку обходу, і "-" - інакше. Напрямок обходу вибирається довільно. Для визначеності виберемо напрямок обходу за годинниковою стрілкою. Запишемо для прикладу друге правило Кірхгофа для контурів ^ ABCFAі ABCDEFA(рис. 15.7): контур ABCFA: I 1 R 1 +I 2 R 2 = E 1 – E 2 ; контур ABCDEFA: I 1 R 1 -I 3 R 3 = E 1 – E 3 . Загалом, коли в ланцюзі є nвузлів та mконтурів, потрібно скласти n-1 рівняння за першим правилом Кірхгофа та m-1 рівняння за другим правилом. 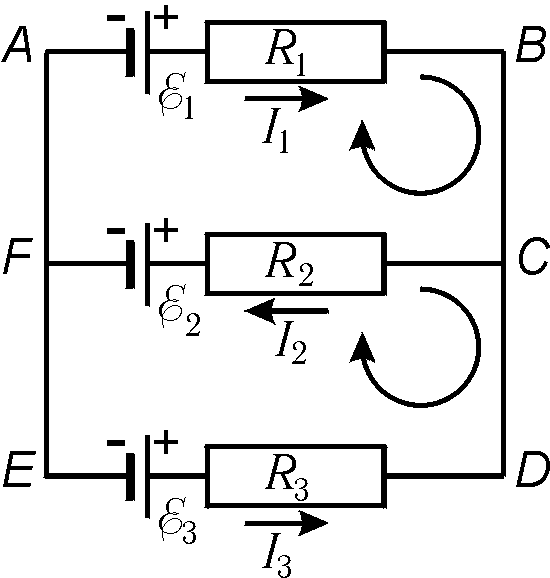 Мал. 15.7 лекція 25. |
1. Енергія системи нерухомих точкових зарядів.Електростатичні сили взаємодії консервативні; отже, система зарядів має потенційну енергію. Знайдемо потенційну енергію системи двох нерухомих точкових зарядів і , що знаходяться на відстані один від одного. Кожен із цих зарядів у полі іншого має потенційну енергію:
, ![]() ,
,
де і - відповідно потенціали, створювані зарядом у точці знаходження заряду та зарядом у точці знаходження заряду . Згідно з формулою (8.3.6),
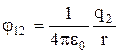 і
і 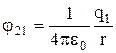 ,
,
![]()
Додаючи до системи з двох зарядів послідовно заряди , , …, можна переконатися, що у разі n нерухомих зарядів енергія взаємодії системи точкових зарядів дорівнює
 , (8.12.1.)
, (8.12.1.)
де - Потенціал, створюваний у тій точці, де знаходиться заряд , усіма зарядами, крім i-го.
2. Енергія зарядженого відокремленого провідника.Нехай є відокремлений провідник, заряд, ємність та потенціал якого відповідно дорівнюють q, C, . Збільшимо заряд цього провідника на dq. Для цього необхідно перенести заряд dq з нескінченності на відокремлений провідник, витративши на це рівну роботу.
![]() .
.
Щоб зарядити тіло від нульового потенціалу до , необхідно здійснити роботу
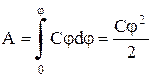 . (8.12.2.)
. (8.12.2.)
Енергія зарядженого провідника дорівнює тій роботі, яку необхідно здійснити, щоб зарядити цей провідник:
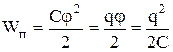 . (8.12.3.)
. (8.12.3.)
Формулу (8.12.3) можна отримати і з того, що потенціал провідника у всіх його точках однаковий, так як поверхня провідника є еквіпотенційною. Вважаючи потенціал провідника рівним, з (8.12.1.) знайдемо
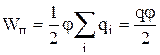 ,
,
де – заряд провідника.
3. Енергія зарядженого конденсатора.Як будь-який заряджений провідник, конденсатор має енергію, яка відповідно до формули (8.12.3.) дорівнює
 , (8.12.4.)
, (8.12.4.)
де q – заряд конденсатора, C – його ємність, – різницю потенціалів між обкладками.
4. Енергія електростатичного поля.Перетворимо формулу (8.12.4.), що виражає енергію плоского конденсатора за допомогою зарядів та потенціалів, скориставшись виразом для ємності плоского конденсатора та різниці потенціалів між його обкладками (). Тоді отримаємо
 , (8.12.5.)
, (8.12.5.)
де V = Sd – обсяг конденсатора. Формула (8.12.5.) показує, що енергія конденсатора виражається через величину, що характеризує електростатичне поле, - напруженість Е.
Формули (8.12.4.) та (8.12.5.) відповідно пов'язують енергію конденсатора із зарядомна його обкладинках та із напруженістю поля.Виникає, звісно, питання локалізації електростатичної енергіїі що є її носієм – заряди чи поле? Відповідь це питання може дати лише досвід. Електростатика вивчає постійні у часі поля нерухомих набоїв, тобто. в ній поля і заряди, що їх зумовили, невіддільні один від одного. Тому електростатика відповісти на ці запитання не може. Подальший розвиток теорії та експерименту показав, що змінні в часі електричні та магнітні поляможуть існувати відокремлено, незалежно від зарядів, що їх збудили, і поширюються в просторі у вигляді електромагнітних хвиль, здібнихпереносити енергію. Це переконливо підтверджує основне положення теорії близькодії про локалізацію енергії в поліі що носієменергії є поле.
Об'ємна щільність енергії електростатичного поля (енергія одиниці об'єму)
 . (8.12.6.)
. (8.12.6.)
Вираз (8.12.6.) справедливий тільки для ізотропного діелектрика,котрому виконується співвідношення: .
Електричну енергію плоского конденсатора можна виразити через напруженість поля між його обкладками:
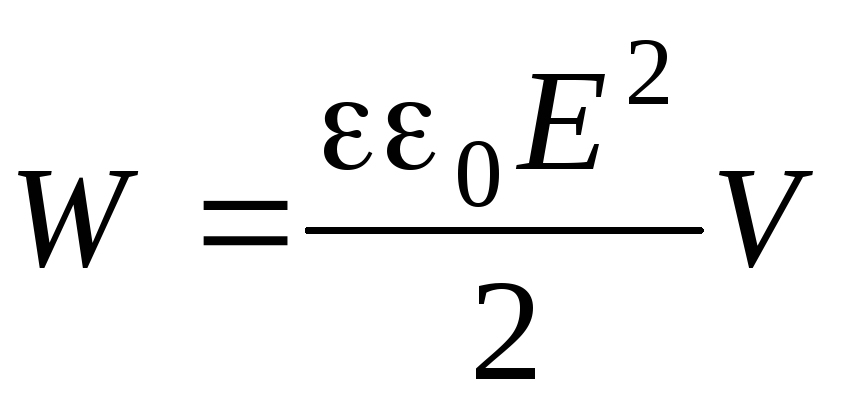 ,
,
де - обсяг простору, зайнятого полем, S- Площа обкладок, d- Відстань між ними. Виявляється, через напруженість можна висловити електричну енергіюта довільної системи заряджених провідників та діелектриків:
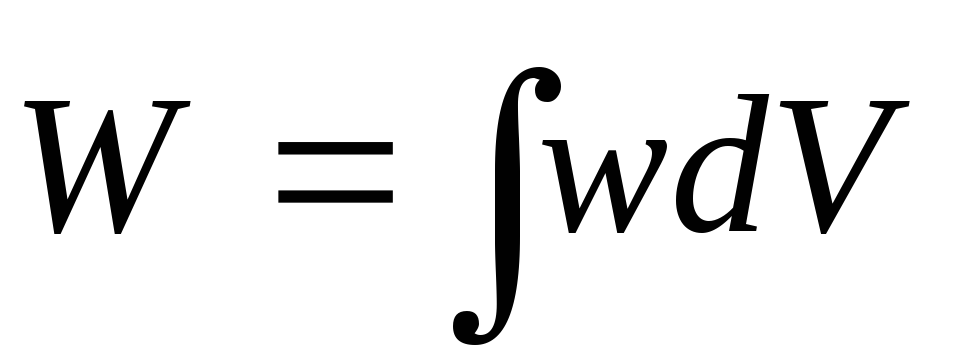 ,
(5)
,
(5)
 ,
,
а інтегрування проводиться по всьому простору, зайнятому полем (передбачається, що діелектрик ізотропний і 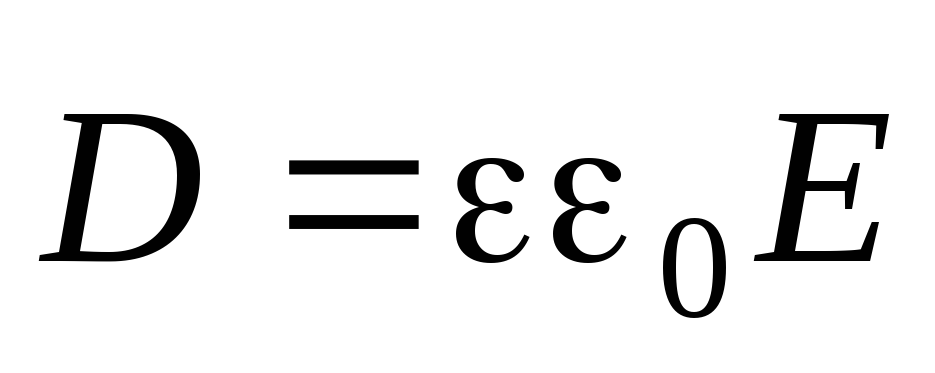 ). Величина wє електричною енергією, що припадає на одиницю об'єму. Вид формули (5) дає підстави припустити, що електрична енергія полягає не у взаємодіючих зарядах, а в їхньому електричному полі, що заповнює простір. В рамках електростатики це припущення перевірити експериментально або обґрунтувати теоретично неможливо, проте розгляд змінних електричних та магнітних полів дозволяє впевнитись у правильності такої польової інтерпретації формули (5).
). Величина wє електричною енергією, що припадає на одиницю об'єму. Вид формули (5) дає підстави припустити, що електрична енергія полягає не у взаємодіючих зарядах, а в їхньому електричному полі, що заповнює простір. В рамках електростатики це припущення перевірити експериментально або обґрунтувати теоретично неможливо, проте розгляд змінних електричних та магнітних полів дозволяє впевнитись у правильності такої польової інтерпретації формули (5).
7. Енергія електричного поля (Приклади розв'язання задач) Енергія взаємодії зарядів
приклад 1.
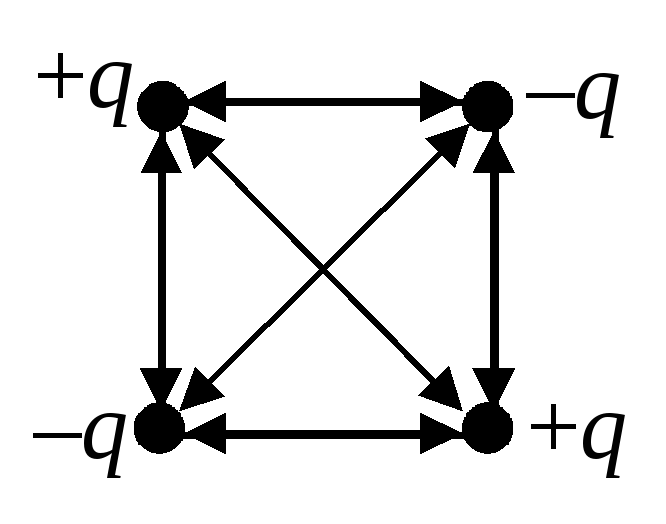
Визначте електричну енергію взаємодії точкових зарядів, що розташовані у вершинах квадрата зі стороною a(Див. рис.2).
Рішення.
На рис.3 умовно зображені двонаправленими стрілками всі парні взаємодії зарядів. Враховуючи енергію всіх цих взаємодій, отримаємо:
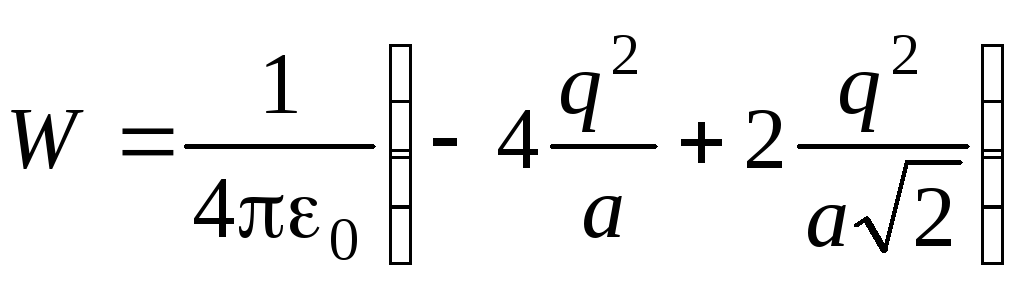 .
.
|
|
|
|
приклад 2.
Визначте електричну енергію взаємодії зарядженого кільця з диполем, розташованим його осі, як показано на рис.4. Відомі відстані a, l, заряди Q, qта радіус кільця R.
Рішення.
При розв'язанні задачі слід врахувати всі енергії парних взаємодій зарядів одного тіла (кільця) із зарядами іншого тіла (диполя). Енергія взаємодії точкового заряду qіз зарядом Q, розподіленим по кільцю, визначається сумою
![]() ,
,
де 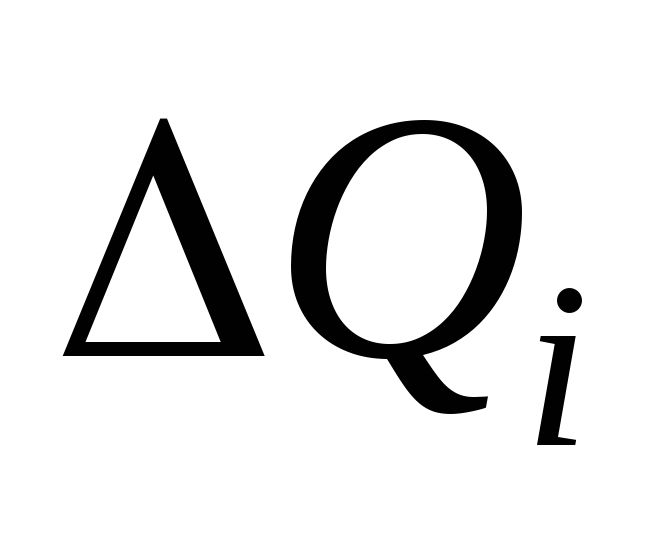 - заряд нескінченно малого фрагмента кільця,
- заряд нескінченно малого фрагмента кільця,
 -
відстань від цього фрагмента до заряду q. Оскільки всі
-
відстань від цього фрагмента до заряду q. Оскільки всі  однакові та рівні
однакові та рівні 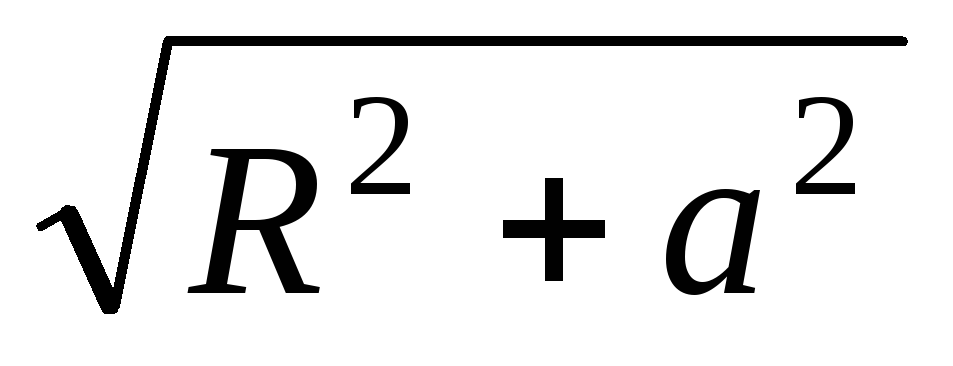 , то
, то
Аналогічно знайдемо енергію взаємодії точкового заряду - qіз зарядженим кільцем:
Підсумовуючи W 1 та W 2 отримаємо для енергії взаємодії кільця з диполем:
 .
.
Електрична енергія заряджених провідників
приклад 3.
Визначте роботу електричних силпри зменшенні у 2 рази радіусу однорідно зарядженої сфери. Заряд сфери q, її початковий радіус R.
Рішення.
Електрична енергія відокремленого провідника визначається формулою 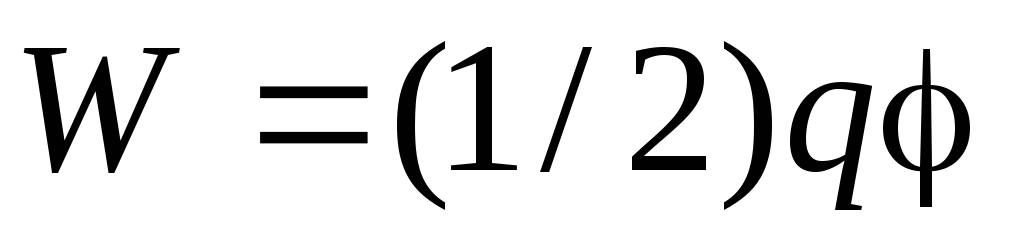 , де q- Заряд провідника, - його потенціал. Враховуючи, що потенціал однорідно зарядженої сфери радіусу Rдорівнює
, де q- Заряд провідника, - його потенціал. Враховуючи, що потенціал однорідно зарядженої сфери радіусу Rдорівнює  , знайдемо її електричну енергію:
, знайдемо її електричну енергію:
 .
.
Після зменшення вдвічі радіусу сфери її енергія стає рівною
 .
.
Електричні сили при цьому виконують роботу
 .
.
приклад 4.
Дві металеві кулі, радіуси яких rі 2 r, а відповідні заряди 2 qі – qрозташовані у вакуумі на великій відстані один від одного. У скільки разів зменшиться електрична енергія системи, якщо кулі з'єднати тонким дротом?
Рішення.
Після з'єднання куль тонким дротом їх потенціали стають однаковими.
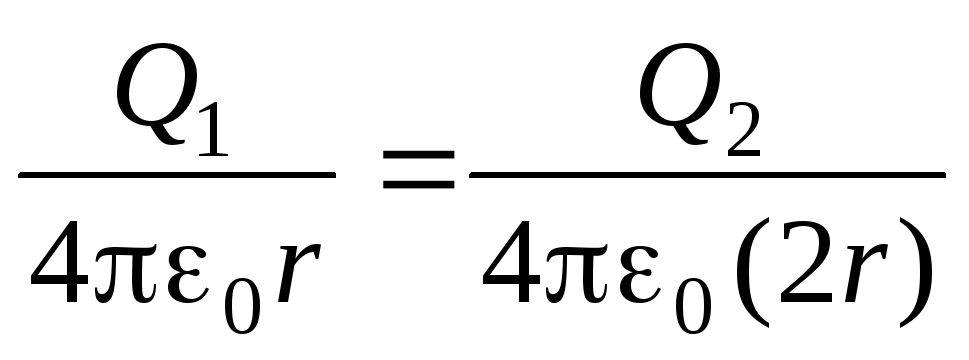 ,
,
а заряди куль, що встановилися Q 1 та Q 2 виходять в результаті перетікання заряду з однієї кулі на іншу. При цьому сумарний заряд куль залишається незмінним:
 .
.
З цих рівнянь знайдемо
 ,
, .
.
Енергія куль до з'єднання їх дротом дорівнює
 ,
,
а після з'єднання
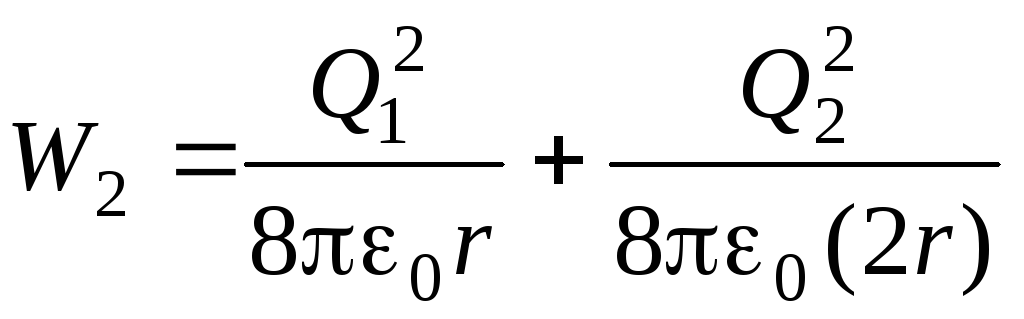 .
.
Підставляючи останній вираз значення Q 1 та Q 2 , отримаємо після простих перетворень
 .
.
Приклад 5.
В одну кулю злилися N= 8 однакових кульок ртуті, заряд кожної з яких q. Вважаючи, що у початковому стані ртутні кульки перебували на великій відстаніодин від одного, визначте, скільки разів збільшилася електрична енергія системи.
Рішення.
При злитті ртутних кульок зберігається їх сумарний заряд та об'єм:
![]() ,
,
де Q- Заряд кулі, R- Його радіус, r– радіус кожної маленької ртутної кульки. Сумарна електрична енергія Nвідокремлених кульок дорівнює
 .
.
Електрична енергія отриманої внаслідок злиття кулі
 .
.
Після алгебраїчних перетворень отримаємо
 = 4.
= 4.
Приклад 6.
Металева кулька радіусу R= 1 мм та заряду q= 0,1 нКл з великої відстані повільно наближають до незарядженого провідника і зупиняють, коли потенціал кульки стає рівним = 450 В. Яку роботу для цього слід здійснити?
Рішення.
Електрична енергія системи із двох заряджених провідників визначається формулою
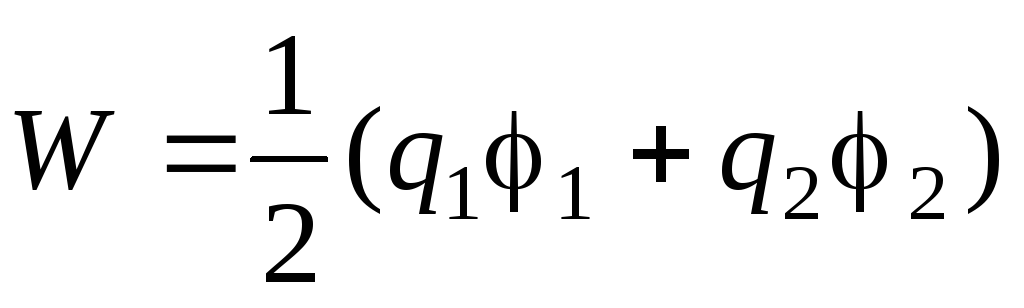 ,
,
де q 1 та q 2 – заряди провідників, 1 та 2 – їх потенціали. Оскільки провідник за умовою завдання не заряджений, то
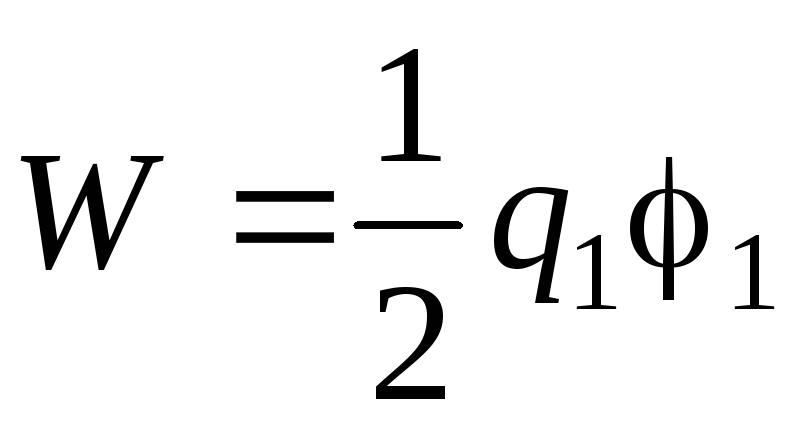 ,
,
де q 1 і 1 заряд та потенціал кулі. Коли куля та незаряджений провідник знаходяться на великій відстані один від одного,
 ,
,
та електрична енергія системи
 .
.
У кінцевому стані системи, коли потенціал кулі став рівним , електрична енергія системи:
 .
.
Робота зовнішніх сил дорівнює приросту електричної енергії:
 = -0,0225 мкДж.
= -0,0225 мкДж.
Зауважимо, що електричне полеу кінцевому стані системи створюється зарядами, індукованими на провіднику, а також зарядами, неоднорідно розподіленими поверхнею металевої кулі. Розрахувати це поле за відомої геометрії провідника і заданому положенні металевої кулі дуже непросто. Нам не потрібно цього робити, оскільки в задачі задана не геометрична конфігурація системи, а потенціал кулі в кінцевому стані.
приклад 7 .
Система складається з двох концентричних тонких металевих оболонок із радіусами. R 1 та R 2
( та відповідними зарядами q 1 та q 2 . Знайдіть електричну енергію Wсистеми. Розгляньте також спеціальний випадок, коли
та відповідними зарядами q 1 та q 2 . Знайдіть електричну енергію Wсистеми. Розгляньте також спеціальний випадок, коли ![]() .
.
Рішення.
Електрична енергія системи із двох заряджених провідників визначається формулою
 .
.
Для вирішення завдання необхідно знайти потенціали внутрішньої (1) та зовнішньої (2) сфер. Це неважко зробити (див. відповідний розділ посібника):
 ,
, .
.
Підставляючи ці висловлювання у формулу для енергії, отримаємо
 .
.
При ![]() енергія дорівнює
енергія дорівнює
 .
.
Питання №1
Електричне поле.Для пояснення природи електричних взаємодій заряджених тіл необхідно допустити наявність у навколишньому заряді просторі фізичного агента, що здійснює цю взаємодію. Відповідно до теорією близькодії, що стверджує, що силові взаємодії між тілами здійснюються за допомогою особливого матеріального середовища, що оточує взаємодіючі тіла і передає будь-які зміни таких взаємодій у просторі з кінцевою швидкістю, таким агентом є електричне поле.
Електричне поле створюється як нерухомими, так і зарядами, що рухаються. Про наявність електричного поля можна судити, перш за все, за його здатністю надавати силову дію на електричні заряди, що рухаються і нерухомі, а також по здатності індукувати електричні заряди на поверхні нейтральних тіл, що проводять.
Поле, яке створюється нерухомими електричними зарядами, називають стаціонарним електричним, або електростатичнимполем. Воно є окремий випадок електромагнітного поля, З допомогою якого здійснюються силові взаємодії між електрично зарядженими тілами, що рухаються в загальному випадку довільним чином щодо системи відліку.
Напруженість електричного поля.Кількісною характеристикою силової дії електричного поля на заряджені тіла є векторна величина E, звана напругою електричного поля.
E= F / qін.
Вона визначається ставленням сили F, що діє з боку поля на точковий пробний заряд qпр, поміщений у точку поля, що розглядається, до величини цього заряду.
Поняття «пробний заряд» передбачає, що цей заряд не бере участі у створенні електричного поля і такий малий, що не спотворює його, тобто не викликає перерозподілу в просторі зарядів, що створюють поле. У системі СІ одиницею напруженості служить 1 В/м, що еквівалентно 1 Н/Кл.
Напруженість поля точкового заряду.Використовуючи закон Кулона, знайдемо вираз для напруженості електричного поля, створюваного точковим зарядом. qв однорідному ізотропному середовищі на відстані rвід заряду:
У цій формулі r- Радіус-вектор, що з'єднує заряди qі qпр. З (1.2) випливає, що напруженість Eполя точкового заряду qу всіх точках поля спрямована радіально від заряду при q> 0 і до заряду при q< 0.
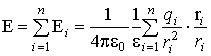 Принцип суперпозиції.Напруженість поля, створюваного системоюнерухомих точкових зарядів q 1 , q 2 , q 3 , ¼, q n, дорівнює векторній сумі напруженостей електричних полів, створюваних кожним із цих зарядів окремо:
Принцип суперпозиції.Напруженість поля, створюваного системоюнерухомих точкових зарядів q 1 , q 2 , q 3 , ¼, q n, дорівнює векторній сумі напруженостей електричних полів, створюваних кожним із цих зарядів окремо:
, де r i- Відстань між зарядом q iі точкою поля, що розглядається.
Принцип суперпозиції, дозволяє розраховувати як напруженість поля системи точкових зарядів, а й напруженість поля у системах, де має місце безперервний розподіл заряду. Заряд тіла можна подати як суму елементарних точкових зарядів d q.
При цьому якщо заряд розподілений з лінійною щільністю t, то d q= td l; якщо заряд розподілений з поверхневою щільністю s, то d q= d lі d q= rd l, якщо заряд розподілено з об'ємною щільністю r.
Питання №2
Потік вектор електричної індукції.Потік вектора електричної індукції визначається аналогічно до потоку вектора напруженості електричного поля
dF D = D d S
У визначеннях потоків помітна деяка неоднозначність, що з кожної поверхні можна задати дві нормалі протилежного напрями. Для замкнутої поверхні позитивною вважається зовнішня нормаль.
Теорема Гауса.Розглянемо точковий позитивний електричний заряд q, що знаходиться всередині замкнутої довільної поверхні S (рис. 1.3). Потік вектора індукції через елемент поверхні dS дорівнює ![]()
Що становить dS D = dS cosa елемента поверхні d Sу напрямку вектора індукції Dрозглядаємо як елемент сферичної поверхні радіусу r, у центрі якої розташований заряд q.
Враховуючи, що dS D / r 2 дорівнює елементарному тілесному куту dw, під яким з точки знаходження заряду q видно елемент поверхні dS, перетворюємо вираз (1.4) до виду dF D = q dw / 4p, звідки після інтегрування по всьому навколишнього заряду простору, тобто в межах тілесного кута від 0 до 4p, отримаємо
Потік вектора електричної індукції через замкнуту поверхню довільної форми дорівнює заряду, укладеному в цій поверхні.
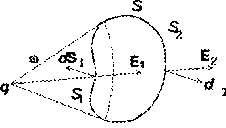
Якщо довільна замкнута поверхня S не охоплює точковий заряд q, то побудувавши конічну поверхню з вершиною в точці знаходження заряду, розділимо поверхню S на дві частини: S 1 і S 2 . Потік вектора Dчерез поверхню S знайдемо як суму алгебри потоків через поверхні S 1 і S 2:
![]() .
.
Обидві поверхні з точки знаходження заряду видно під одним тілесним кутом w. Тому потоки рівні
Оскільки при обчисленні потоку через замкнуту поверхню використовується зовнішня нормаль до поверхні, легко бачити, що потік Ф 1D< 0, тогда как поток Ф 2D >0. Сумарний потік Ф D = 0. Це означає, що потік вектора електричної індукції через замкнуту поверхню довільної форми не залежить від зарядів, розташованих поза цією поверхнею.
Якщо електричне поле створюється системою точкових зарядів q 1 , q 2 ,¼, q n , яка охоплюється замкнутою поверхнею S, то відповідно до принципу суперпозиції, потік вектора індукції через цю поверхню визначається як сума потоків, створюваних кожним із зарядів. Потік вектора електричної індукції через замкнуту поверхню довільної форми дорівнює сумі алгебри зарядів, охоплених цією поверхнею:
Слід зазначити, що заряди q i не обов'язково мають бути точковими, необхідна умова- Заряджена область повинна повністю охоплюватися поверхнею. Якщо просторі, обмеженому замкнутої поверхнею S, електричний заряд розподілений безперервно, слід вважати, кожен елементарний обсяг dV має заряд . У цьому випадку в правій частині виразу алгебраїчне підсумовування зарядів замінюється інтегруванням за обсягом, укладеним усередині замкнутої поверхні S:
Цей вираз є найбільш загальним формулюванням теореми Гауса: потік вектора електричної індукції через замкнуту поверхню довільної форми дорівнює сумарному заряду в обсязі, охопленому цією поверхнею, і не залежить від зарядів, розташованих поза розглянутою поверхнею ![]() .
.
Питання №3
Потенційна енергія заряду у електричному полі.Роботу, що здійснюється силами електричного поля при переміщенні позитивного точкового заряду qіз положення 1 у положення 2, представимо як зміну потенційної енергії цього заряду: ![]() , де Wп1 та Wп2 – потенційні енергії заряду qу положеннях 1 та 2. При малому переміщенні заряду qу полі, створюваному позитивним точковим зарядом Qзміна потенційної енергії дорівнює
, де Wп1 та Wп2 – потенційні енергії заряду qу положеннях 1 та 2. При малому переміщенні заряду qу полі, створюваному позитивним точковим зарядом Qзміна потенційної енергії дорівнює ![]() . При кінцевому переміщенні заряду qіз положення 1 до положення 2, що знаходяться на відстанях r 1 та r 2 від заряду Q, . Якщо поле створено системою точкових зарядів Q 1 ,Q 2 ,¼, Q n, то зміна потенційної енергії заряду qу цьому полі:
. При кінцевому переміщенні заряду qіз положення 1 до положення 2, що знаходяться на відстанях r 1 та r 2 від заряду Q, . Якщо поле створено системою точкових зарядів Q 1 ,Q 2 ,¼, Q n, то зміна потенційної енергії заряду qу цьому полі:  . Наведені формули дозволяють знайти тільки змінапотенційної енергії точкового заряду q, а чи не саму потенційну енергію. Для визначення потенційної енергії необхідно домовитись, у якій точці поля вважати її рівною нулю. Для потенційної енергії точкового заряду q, що знаходиться в електричному полі, створеному іншим точковим зарядом Q, отримаємо
. Наведені формули дозволяють знайти тільки змінапотенційної енергії точкового заряду q, а чи не саму потенційну енергію. Для визначення потенційної енергії необхідно домовитись, у якій точці поля вважати її рівною нулю. Для потенційної енергії точкового заряду q, що знаходиться в електричному полі, створеному іншим точковим зарядом Q, отримаємо
![]() , де C- Довільна постійна. Нехай потенційна енергія дорівнює нулю на нескінченно великій відстані від заряду Q(при r® ¥), тоді постійна C= 0 і попередній вираз набуває вигляду. При цьому потенційна енергія визначається як робота переміщення заряду силами поля з цієї точки до нескінченно віддаленої.У разі електричного поля, створюваного системою точкових зарядів, потенційна енергія заряду q:
, де C- Довільна постійна. Нехай потенційна енергія дорівнює нулю на нескінченно великій відстані від заряду Q(при r® ¥), тоді постійна C= 0 і попередній вираз набуває вигляду. При цьому потенційна енергія визначається як робота переміщення заряду силами поля з цієї точки до нескінченно віддаленої.У разі електричного поля, створюваного системою точкових зарядів, потенційна енергія заряду q:
![]() .
.
![]() Потенційна енергія системи точкових набоїв.У разі електростатичного поля потенційна енергія є мірою взаємодії зарядів. Нехай у просторі існує система точкових зарядів Q i(i = 1, 2, ... , n). Енергія взаємодії всіх nзарядів визначиться співвідношенням, де r ij -відстань між відповідними зарядами, а підсумовування здійснюється таким чином, щоб взаємодія між кожною парою зарядів враховувалася один раз.
Потенційна енергія системи точкових набоїв.У разі електростатичного поля потенційна енергія є мірою взаємодії зарядів. Нехай у просторі існує система точкових зарядів Q i(i = 1, 2, ... , n). Енергія взаємодії всіх nзарядів визначиться співвідношенням, де r ij -відстань між відповідними зарядами, а підсумовування здійснюється таким чином, щоб взаємодія між кожною парою зарядів враховувалася один раз.
Потенціал електростатичного поля.Поле консервативної сили може бути описано не тільки векторною функцією, але еквівалентний опис цього поля можна отримати, визначивши в кожній його точці відповідну скалярну величину. Для електростатичного поля такою величиною є потенціал електростатичного поля, що визначається як відношення потенційної енергії пробного заряду qдо величини цього заряду, j = Wп / q, Звідки випливає, що потенціал чисельно дорівнює потенційній енергії, якою володіє в цій точці поля одиничний позитивний заряд. Одиницею виміру потенціалу служить Вольт (1 У).
Потенціал поля точкового зарядуQв однорідному ізотропному середовищі з діелектричною проникністю e: .
![]()
![]() Принцип суперпозиції.Потенціал є скалярною функцією, для неї справедливий принцип суперпозиції. Так для потенціалу поля системи точкових зарядів Q 1, Q 2 ¼, Q nмаємо, де r i- відстань від точки поля, що має потенціал j, до заряду Q i. Якщо заряд довільним чином розподілено у просторі, то де r- Відстань від елементарного об'єму d x, d y, d zдо точки ( x, y, z), де визначається потенціал; V- Обсяг простору, в якому розподілений заряд.
Принцип суперпозиції.Потенціал є скалярною функцією, для неї справедливий принцип суперпозиції. Так для потенціалу поля системи точкових зарядів Q 1, Q 2 ¼, Q nмаємо, де r i- відстань від точки поля, що має потенціал j, до заряду Q i. Якщо заряд довільним чином розподілено у просторі, то де r- Відстань від елементарного об'єму d x, d y, d zдо точки ( x, y, z), де визначається потенціал; V- Обсяг простору, в якому розподілений заряд.
Потенціал та робота сил електричного поля.Грунтуючись на визначенні потенціалу, можна показати, що робота сил електричного поля під час переміщення точкового заряду qз однієї точки поля в іншу дорівнює добутку величини цього заряду на різницю потенціалів у початковій та кінцевій точках шляху, A = q(J 1 - j 2).
Визначення зручно записати так:
Питання №4
Для встановлення зв'язку між силовою характеристикою електричного поля - напруженістюта його енергетичною характеристикою - потенціаломрозглянемо елементарну роботу сил електричного поля на нескінченно малому переміщенні точкового заряду q: d A = qE d l, ця ж робота дорівнює втраті потенційної енергії заряду q: d A = - d Wп = - q d де d - Зміна потенціалу електричного поля на довжині переміщення d l. Прирівнюючи праві частини виразів, отримуємо: E d l= -d чи декартової системі координат
E x d x + E y d y + E z d z =-d, (1.8)
де E x,E y,E z- Проекції вектора напруженості на осі системи координат. Оскільки вираз (1.8) є повним диференціалом, то для проекцій вектора напруженості маємо
![]() звідки.
звідки.
Вираз, що стоїть у дужках градієнтомпотенціалу j, тобто.
E= - grad = -Ñ.
Напруженість у будь-якій точці електричного поля дорівнює градієнту потенціалу в цій точці, взятому зі зворотним знаком. Знак "мінус" вказує, що напруженість Eспрямована у бік зменшення потенціалу.
Розглянемо електричне поле, яке створюється позитивним точковим зарядом q(Рис. 1.6). Потенціал поля у точці М, положення якої визначається радіус-вектором r, дорівнює = q/ 4pe 0 e r. Напрямок радіус-вектора rзбігається із напрямком вектора напруженості E, А градієнт потенціалу спрямований у протилежний бік. Проекція градієнта на напрямок радіус-вектора
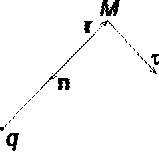
![]() . Проекція ж градієнта потенціалу на напрямок вектора t, перпендикулярного вектору r, дорівнює
. Проекція ж градієнта потенціалу на напрямок вектора t, перпендикулярного вектору r, дорівнює ![]() ,
,
тобто в цьому напрямку потенціал електричного поля є постійною величиною(= const).
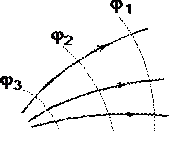 У розглянутому випадку напрям вектора rзбігається з напрямком
У розглянутому випадку напрям вектора rзбігається з напрямком
силових ліній. Узагальнюючи отриманий результат, можна стверджувати, що у всіх точках кривої, ортогональній до силових ліній, потенціал електричного поля однаковий. Геометричним місцем точок з однаковим потенціалом є еквіпотенційна поверхня, ортогональна до силових ліній.
При графічному зображенні електричних полів часто використовують еквіпотенційні поверхні. Зазвичай еквіпотенціалі проводять таким чином, щоб різниця потенціалів між будь-якими двома еквіпотенційними поверхнями була однакова. Тут наведено двомірну картину електричного поля. Силові лінії показані суцільними лініями, еквіпотенціалі – штриховими.
Подібне зображення дозволяє сказати, в який бік спрямований вектор напруги електричного поля; де напруженість більша, де менша; куди почне рухатись електричний заряд, поміщений у ту чи іншу точку поля. Оскільки всі точки еквіпотенційної поверхні знаходяться при однаковому потенціалі, переміщення заряду вздовж неї не вимагає роботи. Це означає, що сила, що діє на заряд, постійно перпендикулярна до переміщення.
Питання №5
Якщо провіднику повідомити надлишковий заряд, цей заряд розподілиться по поверхні провідника. Дійсно, якщо всередині провідника виділити довільну замкнуту поверхню S, то потік вектора напруженості електричного поля через цю поверхню повинен дорівнювати нулю. В іншому випадку всередині провідника існуватиме електричне поле, що призведе до переміщення зарядів. Отже, для того, щоб виконувалася умова
Сумарний електричний заряд усередині цієї довільної поверхні повинен дорівнювати нулю.
Напруженість електричного поля поблизу поверхні зарядженого провідника можна визначити за допомогою теореми Гауса. Для цього виділимо на поверхні провідника малу довільну площадку d Sі, вважаючи її за основу, побудуємо на ній циліндр із твірною d l(Рис. 3.1). На поверхні провідника вектор Еспрямований нормалі до цієї поверхні. Тому потік вектора Ечерез бічну поверхню циліндра через трохи d lдорівнює нулю. Потік цього вектора через нижню основу циліндра, що знаходиться всередині провідника, також дорівнює нулю, оскільки всередині провідника електричне поле відсутнє. Отже, потік вектора Ечерез всю поверхню циліндра дорівнює потоку через його верхня основа d S ": , де Е n - проекція вектора напруженості електричного поля на зовнішню нормаль nдо майданчика d S. 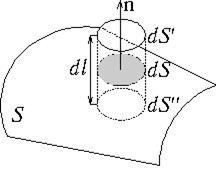
За теореми Гаусса, цей потік дорівнює сумі алгебри електричних зарядів, охоплюваних поверхнею циліндра, віднесеної до твору електричної постійної і відносної діелектричної проникності середовища, навколишнього провідник. Усередині циліндра знаходиться заряд , де поверхнева щільність зарядів. Отже ![]() і , Т. Е. Напруженість електричного поля поблизу поверхні зарядженого провідника прямо пропорційна поверхневої щільності електричних зарядів, що знаходяться на цій поверхні.
і , Т. Е. Напруженість електричного поля поблизу поверхні зарядженого провідника прямо пропорційна поверхневої щільності електричних зарядів, що знаходяться на цій поверхні.
Експериментальні дослідження розподілу надлишкових зарядів на провідниках різної формипоказали, що розподіл зарядів на зовнішній поверхні провідника залежить лише від форми поверхні: що більше кривизна поверхні (що менше радіус кривизни), то більше вписувалося поверхнева щільність заряду.
Поблизу ділянок з малими радіусами кривизни, особливо біля вістря, через високі значення напруженості відбувається іонізація газу, наприклад, повітря. В результаті однойменні із зарядом провідника іони рухаються в напрямку від поверхні провідника, а іони протилежного знакадо поверхні провідника, що призводить до зменшення заряду провідника. Це явище отримало назву стікання заряду.
На внутрішніх поверхнях замкнутих порожніх провідників надлишкові заряди відсутні.
Якщо заряджений провідник привести до контакту з зовнішньою поверхнеюнезарядженого провідника, то заряд перерозподілятиметься між провідниками до того часу, поки їх потенціали стануть рівними.
Якщо ж той самий заряджений провідник стосується внутрішньої поверхніпорожнього провідника, то заряд передається полому провіднику повністю.
На закінчення відзначимо ще одне явище, властиве лише провідникам. Якщо незаряджений провідник помістити у зовнішнє електричне поле, його протилежні частини у напрямі поля матимуть заряди протилежних знаків. Якщо, не знімаючи зовнішнього поля, провідник розділити, розділені частини матимуть різноіменні заряди. Це явище отримало назву електростатичної індукції.
Питання №8
Всі речовини відповідно до їх здатності проводити електричний струм поділяються на провідники, діелектрикиі напівпровідники. Провідниками називають речовини, у яких електрично заряджені частинки - носії заряду- здатні вільно пересуватися по всьому об'єму речовини. До провідників відносяться метали, розчини солей, кислот і лугів, розплавлені солі, іонізовані гази.
Обмежимо розгляд твердими металевими провідниками, що мають кристалічну структуру. Експерименти показують, що при дуже малій різниці потенціалів, прикладеної до провідника, що містяться в ньому електрони провідності, починають рухатися і переміщуються за обсягом металів практично вільно.
У відсутність зовнішнього електростатичного поля електричні поля позитивних іонів і електронів провідності взаємно компенсовані, так що напруженість внутрішнього результуючого поля дорівнює нулю.
При внесенні металевого провідника до зовнішнього електростатичного поля з напруженістю Е 0на іони та вільні електрони починають діяти кулонівські сили, спрямовані у протилежні сторони. Ці сили викликають усунення заряджених частинок усередині металу, причому в основному зміщуються вільні електрони, а позитивні іони, що знаходяться у вузлах кристалічної решітки, практично не змінюють свого положення. В результаті всередині провідника виникає електричне поле з напруженістю Е ".
Зміщення заряджених частинок усередині провідника припиняється тоді, коли сумарна напруженість поля Еу провіднику, що дорівнює сумі напруженостей зовнішнього та внутрішнього полів, стане рівною нулю: ![]()
Представимо вираз, що зв'язує напруженість та потенціал електростатичного поля, у наступному вигляді:
де Е- Напруженість результуючого поля всередині провідника; n- Внутрішня нормаль до поверхні провідника. З рівності нулю результуючої напруженості Еслід, що в межах обсягу провідника потенціал має одне й те саме значення: .
Отримані результати дозволяють зробити три важливі висновки:
1. У всіх точках всередині провідника напруженість поля, тобто весь обсяг провідника еквіпотенційний.
2. При статичному розподілі зарядів за провідником вектор напруженості Ена його поверхні повинен бути спрямований нормалі до поверхні , в іншому випадку під дією дотичної до поверхні провідника компоненти напруженості заряди повинні переміщатися по провіднику.
3. Поверхня провідника також еквіпотенційна, тому що для будь-якої точки поверхні
![]()
Запитання №10
Якщо два провідники мають таку форму, що створюване ними електричне поле зосереджено в обмеженій області простору, то утворена ними система має назву конденсатора, а самі провідники називають обкладкамиконденсатора.
Сферичний конденсатор.Два провідники, що мають форму концентричних сфер з радіусами R 1 та R 2 (R 2 > R 1) утворюють сферичний конденсатор. Використовуючи теорему Гауса, легко показати, що електричне поле існує лише у просторі між сферами. Напруженість цього поля ![]() ,
,
де q- Електричний заряд внутрішньої сфери; - відносна діелектрична проникність середовища, що заповнює простір між обкладками; r- відстань від центру сфер, причому R 1 r R 2 . Різниця потенціалів між обкладками  та ємність сферичного конденсатора.
та ємність сферичного конденсатора.
Циліндричний конденсаторявляє собою два провідні коаксіальні циліндри радіусами. R 1 та R 2 (R 2 > R 1). Нехтуючи крайовими ефектами на торцях циліндрів і вважаючи, що простір між обкладками заповнено діелектричним середовищем з відносною проникністю, напруженість поля всередині конденсатора можна знайти за формулою: ![]() ,
,
де q- Заряд внутрішнього циліндра; h- Висота циліндрів (обкладок); r- Відстань від осі циліндрів. Відповідно, різниця потенціалів між обкладками циліндричного конденсатора та його ємність є 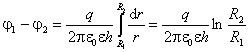 . .
. .
Плоский конденсатор.Дві плоскі паралельні пластини однакової площі Sрозташовані на відстані dодин від одного, утворюють плоский конденсатор. Якщо простір між пластинами заповнено середовищем із відносною діелектричною проникністю, то при повідомленні їм заряду qнапруженість електричного поля між пластинами дорівнює, різниця потенціалів дорівнює. Таким чином, ємність плоского конденсатора.
Послідовне та паралельне з'єднання конденсаторів.
При послідовному з'єднанні nконденсаторів сумарна ємність системи дорівнює
Паралельне з'єднання nконденсаторів утворює систему, електроємність якої можна обчислити так:
Запитання №11
Енергія зарядженого провідника.Поверхня провідника є еквіпотенційною. Тому потенціали тих точок, у яких знаходяться точкові заряди d q, однакові та рівні потенціалу провідника. Заряд q, що знаходиться на провіднику, можна розглядати як систему точкових зарядів d q. Тоді енергія зарядженого провідника
Взявши до уваги визначення ємності, можна записати
Будь-який із цих виразів визначає енергію зарядженого провідника.
Енергія зарядженого конденсатора.Нехай потенціал обкладання конденсатора, на якій знаходиться заряд + q, дорівнює , а потенціал обкладки, на якій знаходиться заряд - q, дорівнює. Енергія такої системи
Енергію зарядженого конденсатора можна у вигляді
Енергія електричного поля.Енергію зарядженого конденсатора можна виразити через величини, що характеризують електричне поле в зазор між обкладками. Зробимо це з прикладу плоского конденсатора. Підстановка виразу для ємності у формулу для енергії конденсатора дає
Приватне U / dдорівнює напруженості поля в зазорі; твір S· dє обсягом Vзаймає поле. Отже, ![]()
Якщо поле однорідне (що має місце в плоскому конденсаторі на відстані dнабагато меншому, ніж лінійні розміри обкладок), то укладена в ньому енергія розподіляється у просторі з постійною щільністю w. Тоді об'ємна щільність енергіїелектричного поля дорівнює
![]()
З урахуванням співвідношення можна записати
В ізотропному діелектрику напрямки векторів Dі Eзбігаються і
Підставимо вираз, отримаємо
Перший доданок у цьому виразі збігається із щільністю енергії поля у вакуумі. Другий доданок є енергією, що витрачається на поляризацію діелектрика. Покажемо це з прикладу неполярного діелектрика. Поляризація неполярного діелектрика полягає в тому, що заряди, що входять до складу молекул, зміщуються зі своїх положень під дією електричного поля. Е. У розрахунку на одиницю обсягу діелектрика робота, що витрачається на усунення зарядів q i на величину d r i , складає
Вираз у дужках є дипольним моментом одиниці об'єму або поляризованістю діелектрика. Р. Отже, .
Вектор Pпов'язаний з вектором Eспіввідношенням. Підставивши цей вираз у формулу для роботи, отримаємо
Провівши інтегрування, визначимо роботу, що витрачається на поляризацію одиниці об'єму діелектрика.
Знаючи густину енергії поля в кожній точці, можна знайти енергію поля, укладеного в будь-якому обсязі V. Для цього потрібно обчислити інтеграл: ![]()
Щільність енергії електростатичного поля
Використовуючи (66), (50), (53), перетворимо формулу енергії конденсатора наступним чином: , де - обсяг конденсатора. Розділимо останній вираз на: ![]() . Величина має сенс густини енергії електростатичного поля.
. Величина має сенс густини енергії електростатичного поля.
Запитання №12
Діелектрик, поміщений у зовнішнє електричне поле, поляризуєтьсяпід впливом цього поля. Поляризацією діелектрика називається процес придбання їм відмінного від нуля макроскопічного дипольного моменту.
Ступінь поляризації діелектрика характеризується векторною величиною, що називається поляризованістюабо вектор поляризації (P). Поляризованість визначається як електричний момент одиниці об'єму діелектрика,
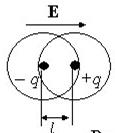 де N- Число молекул в обсязі. Поляризованість Pчасто називають поляризацією, розуміючи під цим кількісний захід цього процесу.
де N- Число молекул в обсязі. Поляризованість Pчасто називають поляризацією, розуміючи під цим кількісний захід цього процесу.
У діелектриках розрізняють такі типи поляризації: електронну, орієнтаційну та ґратову (для іонних кристалів).
Електронний тип поляризаціїхарактерний для діелектриків із неполярними молекулами. У зовнішньому електричному полі позитивні заряди всередині молекули зміщуються у напрямку поля, а негативні у протилежному напрямку, внаслідок чого молекули набувають дипольного моменту, спрямованого вздовж зовнішнього поля
 Індукований дипольний момент молекули пропорційний напруженості зовнішнього електричного поля , де - Поляризованість молекули. Значення поляризованості в цьому випадку дорівнює де n- Концентрація молекул; - індукований дипольний момент молекули, однаковий всім молекул і напрям якого збігається з напрямом зовнішнього поля.
Індукований дипольний момент молекули пропорційний напруженості зовнішнього електричного поля , де - Поляризованість молекули. Значення поляризованості в цьому випадку дорівнює де n- Концентрація молекул; - індукований дипольний момент молекули, однаковий всім молекул і напрям якого збігається з напрямом зовнішнього поля.
Орієнтаційний тип поляризаціїхарактерний для полярних діелектриків. За відсутності зовнішнього електричного поля молекулярні диполі орієнтовані випадковим чином, тому макроскопічний електричний момент діелектрика дорівнює нулю.
 Якщо помістити такий діелектрик у зовнішнє електричне поле, то на молекулу-диполь діятиме момент сил (рис. 2.2), що прагне орієнтувати її дипольний момент у напрямку напруженості поля. Проте повної орієнтації немає, оскільки тепловий рух прагне зруйнувати дію зовнішнього електричного поля.
Якщо помістити такий діелектрик у зовнішнє електричне поле, то на молекулу-диполь діятиме момент сил (рис. 2.2), що прагне орієнтувати її дипольний момент у напрямку напруженості поля. Проте повної орієнтації немає, оскільки тепловий рух прагне зруйнувати дію зовнішнього електричного поля.
Така поляризація називається орієнтаційною. Поляризованість у цьому випадку дорівнює де<p> - середнє значення складової дипольного моменту молекули у бік зовнішнього поля.
Гратковий тип поляризаціїхарактерний для іонних кристалів. В іонних кристалах (NaCl і т.д.) без зовнішнього поля дипольний момент кожного елементарного осередку дорівнює нулю (рис. 2.3.а), під впливом зовнішнього електричного поля позитивні і негативні іони зміщуються в протилежні сторони (рис. 2.3.б) . Кожен осередок кристала стає диполем, кристал поляризується. Така поляризація називається решіткової. Поляризованість і в цьому випадку можна визначити як , де значення дипольного моменту елементарного осередку, n- Число осередків в одиниці обсягу.
Поляризованість ізотропних діелектриків будь-якого типу пов'язана з напруженістю поля співвідношенням , де - діелектрична сприйнятливістьдіелектрика.
Запитання №13
Поляризованість середовища має примітну властивість: потік вектора поляризованості середовища через довільну замкнуту поверхню чисельно дорівнює величині некомпенсованих "пов'язаних" зарядів усередині цієї поверхні, взятої зі зворотним знаком:
![]() (1). У локальному формулюванні описувана властивість описується співвідношенням
(1). У локальному формулюванні описувана властивість описується співвідношенням
(2) де - об'ємна щільність "пов'язаних" зарядів. Ці співвідношення називають теоремою Гауса для поляризованості середовища (вектора поляризації) в інтегральній та диференційній формах відповідно. Якщо теорема Гауса для напруженості електричного поля є наслідком закону Кулона в "польовий" формі, теорема Гауса для поляризованості є наслідком визначення цієї величини.
Доведемо співвідношення (1), тоді співвідношення (2) виявиться справедливим через математичну теорему Остроградського-Гаусса.
Розглянемо діелектрик із неполярних молекул з об'ємною концентрацією останніх, що дорівнює . Вважаємо, що під дією електричного поля позитивні заряди змістилися з положення рівноваги на величину, а негативні – на величину. Кожна молекула набула електричного моменту. ![]() , а одиничний обсяг набув електричного моменту . Розглянемо довільну досить гладку замкнуту поверхню в описуваному діелектрику. Припустимо, що поверхня проведена так, що відсутність електричного поля вона "не перетинає" окремі диполі, тобто позитивний і негативний заряди, пов'язані з молекулярною структурою речовини, "компенсують" один одного.
, а одиничний обсяг набув електричного моменту . Розглянемо довільну досить гладку замкнуту поверхню в описуваному діелектрику. Припустимо, що поверхня проведена так, що відсутність електричного поля вона "не перетинає" окремі диполі, тобто позитивний і негативний заряди, пов'язані з молекулярною структурою речовини, "компенсують" один одного.
Зауважимо, до речі, що співвідношення (1) і (2) при і задовольняються тотожно.
Під дією електричного поля елемент площі поверхні перетнуть позитивні заряди з об'єму в кількості. Для негативних зарядів маємо відповідно величини та . Сумарний заряд, що перейшов на "зовнішню" сторону елемента площі поверхні (нагадаємо, що - зовнішня нормаль щодо охоплюваного поверхнею обсягу) дорівнює
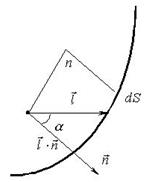
Властивості вектора поляризованості середовища
Проінтегрувавши отриманий вираз по замкнутій поверхні отримаємо величину сумарного електричного заряду, що залишив аналізований обсяг. Останнє дозволяє укласти, що в обсязі, що розглядається, залишився некомпенсований заряд - , рівний по модулю заряду, що пішов. У результаті маємо: ![]() , таким чином, теорема Гауса для векторного поля в інтегральному формулюванні доведена.
, таким чином, теорема Гауса для векторного поля в інтегральному формулюванні доведена.
Щоб розглянути випадок речовини, що складається з полярних молекул, достатньо в наведених вище міркуваннях величину замінити на її середнє значення.
Доказ справедливості співвідношення (1) вважатимуться закінченим.
Запитання №14
У діелектричному середовищі можуть бути електричні заряди двох типів: "вільні" і "пов'язані". Перші їх пов'язані з молекулярної структурою речовини і, зазвичай, можуть щодо вільно переміщатися у просторі. Другі пов'язані з молекулярною структурою речовини і під впливом електричного поля можуть зміщуватися з положення рівноваги, зазвичай, дуже малі відстані.
Використання безпосередньо теореми Гауса для векторного поля при описі діелектричного середовища незручно тим, що права частина формули
![]() (1), містить як величину "вільного", так і величину "пов'язаного" (некомпенсованого) зарядів усередині замкнутої поверхні.
(1), містить як величину "вільного", так і величину "пов'язаного" (некомпенсованого) зарядів усередині замкнутої поверхні.
Якщо співвідношення (1) почленно скласти із співвідношенням ![]() , отримаємо
, отримаємо ![]() , (2)
, (2)
де - сумарний "вільний" заряд об'єму, що охоплюється замкненою поверхнею. Співвідношення (2) зумовлює доцільність запровадження спеціального вектора
Як зручна розрахункова величина, що характеризує електричне поле в діелектричному середовищі. Вектор раніше називали вектором електричної індукції або вектором електричного усунення. В даний час входить у вжиток термін "вектор". Для векторного поля справедлива інтегральна форма теореми Гауса: ![]() і, відповідно, диференціальна форма теореми Гауса:
і, відповідно, диференціальна форма теореми Гауса:
де – об'ємна щільність вільних зарядів.
Якщо справедливе співвідношення (для жорстких електретів воно не справедливе), то для вектора визначення (3) слід ,
де - Діелектрична проникність середовища, одна з найважливіших електричних характеристик речовини. У електростатиці та квазістаціонарній електродинаміці величина є дійсною. При розгляді високочастотних коливальних процесів фаза коливання вектора, а значить і вектора, може не збігатися з фазою коливань вектора, у таких випадках величина стає комплекснозначною величиною.
Розглянемо питання, за яких умов у діелектричному середовищі можлива поява некомпенсованої об'ємної густини пов'язаних зарядів. Для цієї мети запишемо вираз вектора поляризації через діелектричну проникність середовища та вектор:
У справедливості якого легко переконатись. Тепер величина, що представляє інтерес, може бути обчислена:
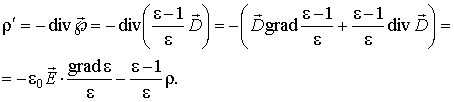 (3)
(3)
За відсутності в діелектричному середовищі об'ємної щільності вільних зарядів величина може звернутися в нуль, якщо
а) відсутня поле; або б) середовище однорідне або в) вектори і - ортогональні. У випадку необхідно обчислити величину по співвідношенням (3).
Запитання №17
 Розглянемо поведінку векторів Eі Dна межі поділу двох однорідних ізотропних діелектриків з проникностями та за відсутності на кордоні вільних зарядів.
Розглянемо поведінку векторів Eі Dна межі поділу двох однорідних ізотропних діелектриків з проникностями та за відсутності на кордоні вільних зарядів.
Граничні умови для нормальних складових векторів D та Eвипливають з теореми Гауса. Виділимо поблизу межі розділу замкнуту поверхню у вигляді циліндра, що утворює якого перпендикулярна до межі розділу, а основи знаходяться на рівній відстані від кордону.
Так як на межі розділу діелектриків немає вільних зарядів, то, відповідно до теорії Гауса, потік вектора електричної індукції через цю поверхню
Виділяючи потоки через основи та бічну поверхню циліндра
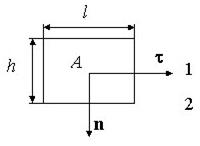 де - значення дотичної складової усереднене по бічній поверхні. Переходячи до межі при (при цьому також прагне нуля), отримуємо
де - значення дотичної складової усереднене по бічній поверхні. Переходячи до межі при (при цьому також прагне нуля), отримуємо ![]() , або остаточно нормальних складових вектора електричної індукції . Для нормальних складових вектора напруженості поля отримаємо
, або остаточно нормальних складових вектора електричної індукції . Для нормальних складових вектора напруженості поля отримаємо ![]() . Таким чином, при переході через кордон розділу діелектричних середовищ нормальна складова вектора терпить розрив, а нормальна складова вектора безперервна.
. Таким чином, при переході через кордон розділу діелектричних середовищ нормальна складова вектора терпить розрив, а нормальна складова вектора безперервна.
Граничні умови для дотичних складових векторів D та Eвипливають із співвідношення, що описує циркуляцію вектора напруженості електричного поля. Побудуємо поблизу межі розділу прямокутний замкнутий контур довжини lта висоти h. Враховуючи, що для електростатичного поля і обходячи контур за годинниковою стрілкою, представимо циркуляцію вектора Eу наступному вигляді: ![]() ,
,
де – середнє значення E nна бокових сторонах прямокутника. Переходячи до межі при , отримаємо для дотичних складових E .
Для дотичних складових вектора електричної індукції гранична умова має вигляд ![]()
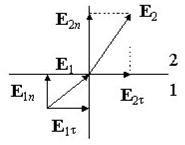 Таким чином, при переході через кордон розділу діелектричних середовищ дотична складова вектора безперервна, а дотична складова вектора терпить розрив.
Таким чином, при переході через кордон розділу діелектричних середовищ дотична складова вектора безперервна, а дотична складова вектора терпить розрив.
Заломлення ліній електричного поля.З граничних умов для відповідних складових векторів Eі Dслід, що з переході через межу розділу двох діелектричних середовищ лінії цих векторів заломлюються (рис. 2.8). Розкладемо вектори E 1і E 2у межі поділу на нормальні та тангенціальні складові та визначимо зв'язок між кутами та за умови. Легко бачити, що як для напруженості поля, так і для індукції справедливий той самий закон заломлення ліній напруженості та ліній зміщення
![]() .
.
При переході в середу з меншим значенням кут, що утворюється лініями напруженості (зміщення) з нормаллю, зменшується, отже, лінії розташовуються рідше. При переході в середу з більшою лінією векторів Eі D, навпаки, згущуються і віддаляються від нормалі.
Питання №6
Теорема про єдиність розв'язання задач електростатики (задані розташування провідників та їх заряди).
Якщо задано розташування провідників у просторі та повний заряд кожного з провідників, то вектор напруженості електростатичного поля у кожній точці визначається єдиним чином. Док-во: (від неприємного)
Нехай заряд на провідниках розподілено так:
Припустимо, що можливе не тільки таке, а й відмінне від нього розподіл зарядів:
(тобто відрізняється як завгодно мало хоча б на одному провіднику)
Отже хоча у одній точці простору знайдеться інший вектор E, тобто. поблизу нових значень густини принаймні в якихось точках E буде чудово. Т.о. при тих же початкових умовах, При тих же провідниках отримаємо інше рішення. Тепер змінимо знак заряду на протилежний.
(міняти знак треба відразу на всіх провідниках)
Вид силових ліній при цьому не зміниться (не суперечить ні теоремі Гаусса, ні теоремі про циркуляцію), зміниться тільки їх напрямок та вектор E.
Тепер візьмемо суперпозицію зарядів (комбінацію двох варіантів зарядів):
(Тобто накладемо один заряд на інший, і зарядимо вже третім способом)
Якщо не збігається хоча б десь із , то хоча б в одному місці отримаємо якесь
 3) відводимо лінії в нескінченність, не замикаючи їх на провіднику. при цьому замкнутий контур L замикаємо на нескінченності. Але і в цьому випадку обхід по силової лініїне дасть нульової циркуляції.
3) відводимо лінії в нескінченність, не замикаючи їх на провіднику. при цьому замкнутий контур L замикаємо на нескінченності. Але і в цьому випадку обхід по силової лініїне дасть нульової циркуляції.
Висновок: отже може бути будь-якої відмінної нуля, отже розподіл зарядів встановлено єдиним чином -> єдиність рішення, тобто. E – знаходимо єдиним чином.
Питання №7
Білет 7. Теорема про єдиність розв'язання задач електростатики. (задані розташування провідників та їх потенціали).Якщо встановлено розташування провідників і потенціал кожного з них, то напруженість електростатичного поля в кожній точці знаходиться єдиним чином.
(Берклеївський курс)
Усюди поза провідником функція повинна задовольняти диференціальне рівняння у приватних похідних: , або, інакше, (2)
Очевидно, що W не задовольняє граничні умови. У поверхні кожного провідника функція W дорівнює нулю, оскільки приймають однакове значення біля поверхні провідника. Отже W є рішенням іншого електростатичного завдання, з тими ж провідниками, але за умови, що всі провідники мають нульовий потенціал. Якщо це так, можна стверджувати, що функція W дорівнює нулю у всіх точках простору. Якщо це не так, то вона повинна мати десь максимум чи мінімум. Шлях W має екстремум у точці P, розглянемо тоді кулю із центром у цій точці. Нам відомо, що середнє значення у сфері функції, що задовольняє рівняння Лапласа, дорівнює значенню функції в центрі. Це несправедливо, якщо центр є максимум або мінімум цієї функції. Таким чином, W не може мати максимуму або мінімуму, вона всюди повинна дорівнювати нулю. Звідси випливає, що =
Запитання №28
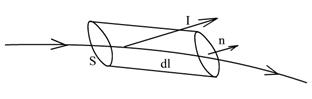 Трм. про циркуляцію в-ра I.
Трм. про циркуляцію в-ра I.
I – вектор намагніченості. I = = N p 1 м = N n i 1 S\c
DV = Sdl cosα; di мол = i 1 мол NSdl cosα = cIdl cosα, N - число мол-л на 1см 3 . Поблизу контуру вважаємо речовину однорідною, тобто всі диполі, всі молекули мають однаковий магнітний момент. Для підрахунку візьмемо молекулу, дро якої розташовано прямо на контурі dl. Треба порахувати, скільки атомів перетнуть циліндрик 1 раз => Це такі, чиї центри лежать усередині цього уяву циліндра. Таким чином нас цікавить лише i мовляв – тобто. струм, що перетинає поверхню, що спирається на контур.
Питання №9
1. Енергія системи точкових нерухомих зарядів . Електростатичні сили консервативні і система зарядів має потенційну енергію. Нехай заряди Q1 і Q2 знаходяться на відстані r один від одного. Кожен із цих зарядів у полі іншого має потенційну енергію.
де φ 12 і φ 21 – відповідно потенціали, створювані зарядом Q 2 у точці знаходження заряду Q 1 і навпаки.
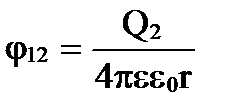 ;
; 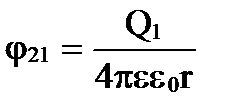 .
.
W 1 = W 2 = W = Q 1 φ 12 = Q 2 φ 21 = ½ (Q 1 φ 12 + Q 2 φ 21).
Додаючи до системи двох зарядів послідовно заряди Q 3 , Q 4 , …, Q n , можна переконатися, що енергія взаємодії системи зарядів дорівнює
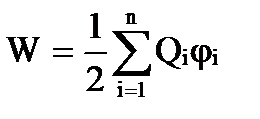 ,
,
де φ i - потенціал, створюваний у тій точці, де знаходиться заряд Q i всіма зарядами, крім i-го.
2. Енергія зарядженого відокремленого провідника . Нехай є відокремлений провідник, заряд, ємність та потенціал якого Q, C, φ.
Збільшимо заряд на dQ. Для цього необхідно перенести заряд dQ з нескінченності до поверхні провідника, витративши на це рівну роботу.
dA = φdQ = C φd φ
Щоб зарядити тіло від нульового потенціалу до потенціалу рівного φ необхідно здійснити роботу
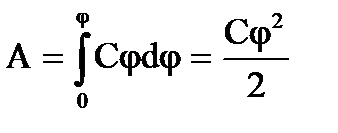
Енергія зарядженого провідника дорівнюватиме цій роботі

Враховуючи що  , цю енергію можна у вигляді
, цю енергію можна у вигляді
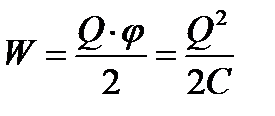
3. Енергія зарядженого конденсатора . Як всякий заряджений провідник, конденсатор має енергію
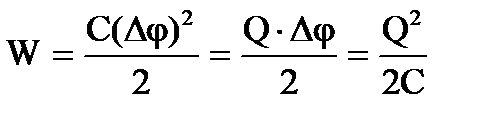
де Q - заряд конденсатора, С – його ємність та Δφ – різниця потенціалів між обкладками.
Використовуючи вираз енергії, можна знайти механічну (пондеромоторную) силу, з якою пластини конденсатора притягують одна одну. Для цього припустимо, що відстань між пластинами змінюється на величину dx. Тоді діюча силаздійснює роботу рівну
за рахунок зменшення потенційної енергії Fdx = - dW, звідки
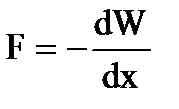 .
.
Підставляючи у формулу енергії 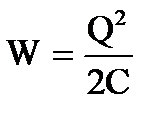 вираз ємності
вираз ємності
 , отримаємо
, отримаємо
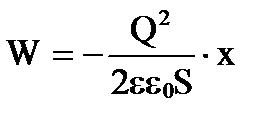 .
.
Диференціюючи W по х, знайдемо силу F
 ,
,
де знак “мінус“ показує, що F прагне зменшити відстань між пластинами, тобто. є силою тяжіння. Підставляючи вираз щільності зарядів на платівках  , отримаємо
, отримаємо 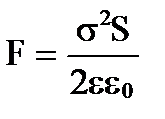 .
.
Враховуючи напруженість поля, що Е =  , отримаємо
, отримаємо
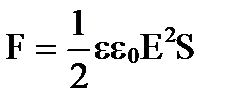 .
.
Тиск на пластини діелектрика, поміщені в зазорі конденсатора, буде
![]()
4. Енергія електростатичного поля.
Перетворимо формулу енергії плоского конденсатора  , використовуючи формули
, використовуючи формули
 та Δφ = Еd.
та Δφ = Еd.
Отримаємо,
де V - обсяг простору між пластинами конденсатора, в якому зосереджена енергія поля W.
Об'ємну щільність енергії поля w – це енергія, що міститься в одиниці об'єму електричного поля і вона дорівнює
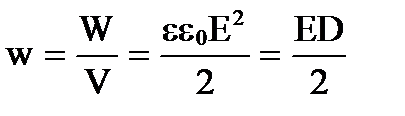 .
.
Одиниця виміру [Дж/м 3].
Видно, що об'ємна щільність енергії поля залежить лише від характеристик поля та середовища.

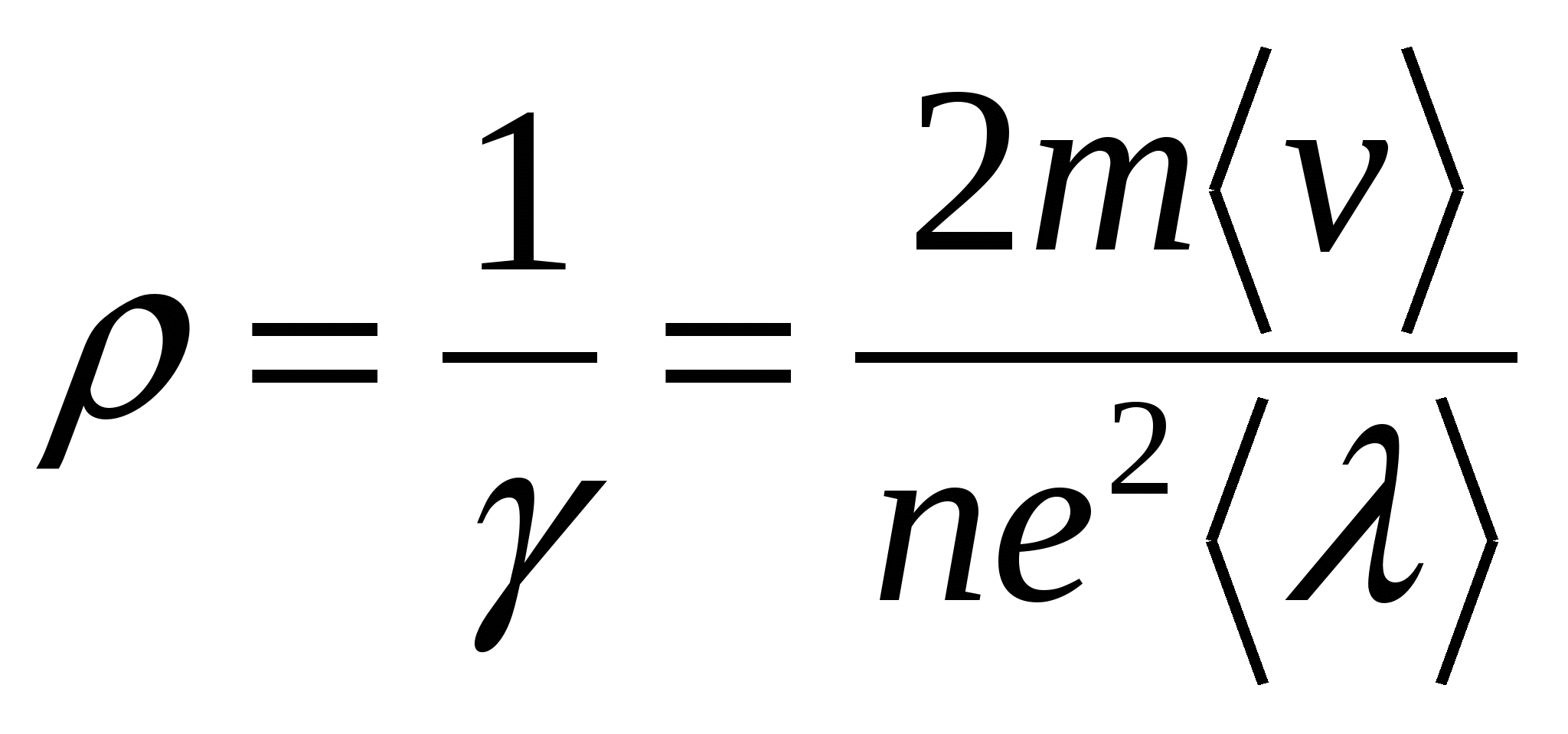 .
. . Цю енергію електрон повністю передає іону кристалічних ґрат при зіткненні з ним. Безліч таких зіткнень призводить до виділення джоулевої теплоти. Якщо концентрація електронів n, і кожен із них стикається
. Цю енергію електрон повністю передає іону кристалічних ґрат при зіткненні з ним. Безліч таких зіткнень призводить до виділення джоулевої теплоти. Якщо концентрація електронів n, і кожен із них стикається  раз за 1 с, то в одиничному обсязі провідника виділитися потужність
раз за 1 с, то в одиничному обсязі провідника виділитися потужність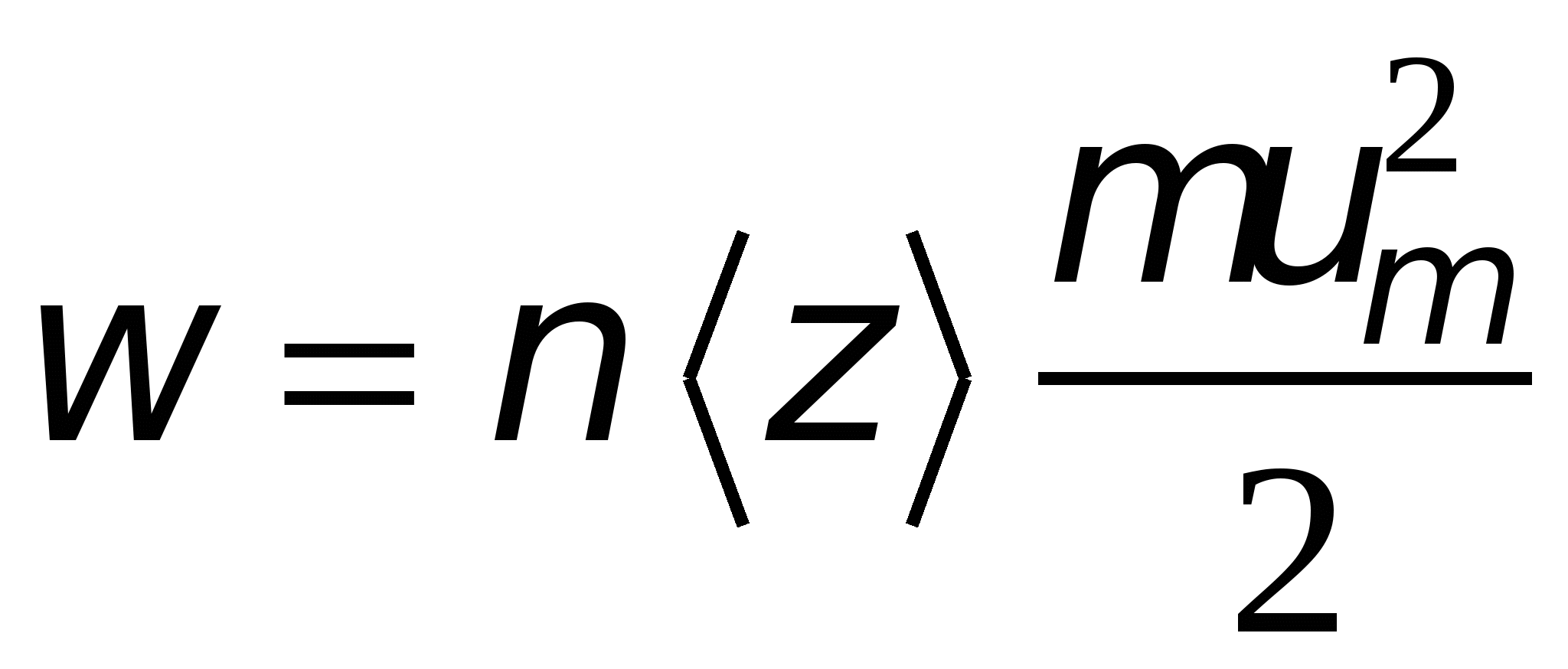 .
.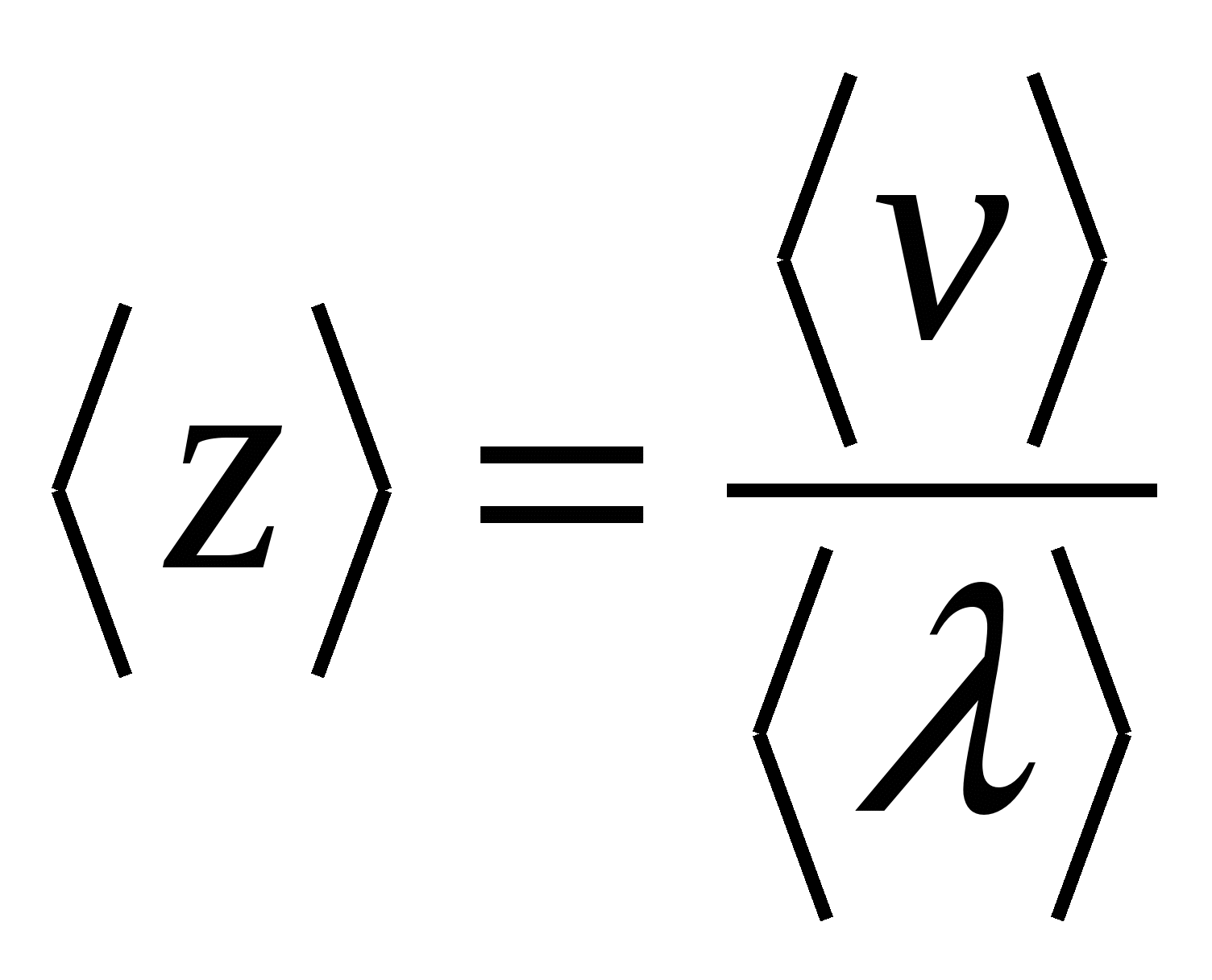 ,
, 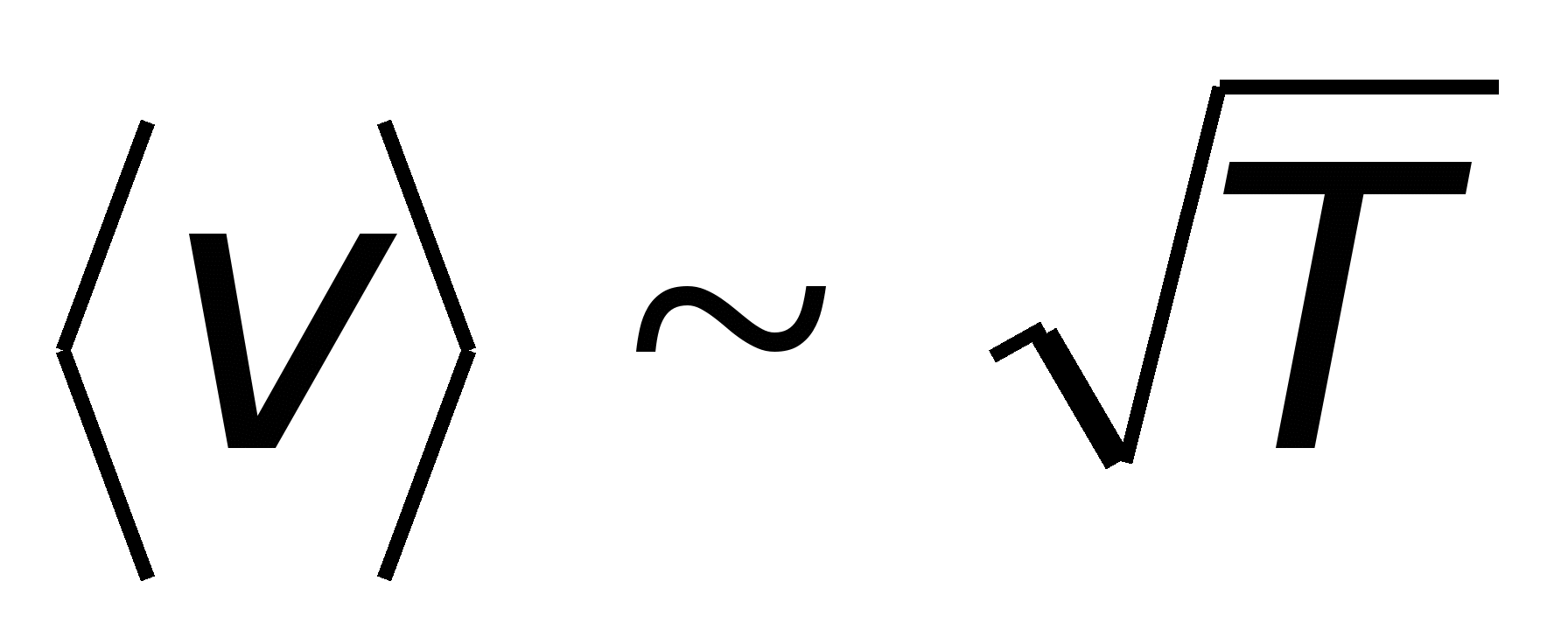 , отже, питомий опір
, отже, питомий опір 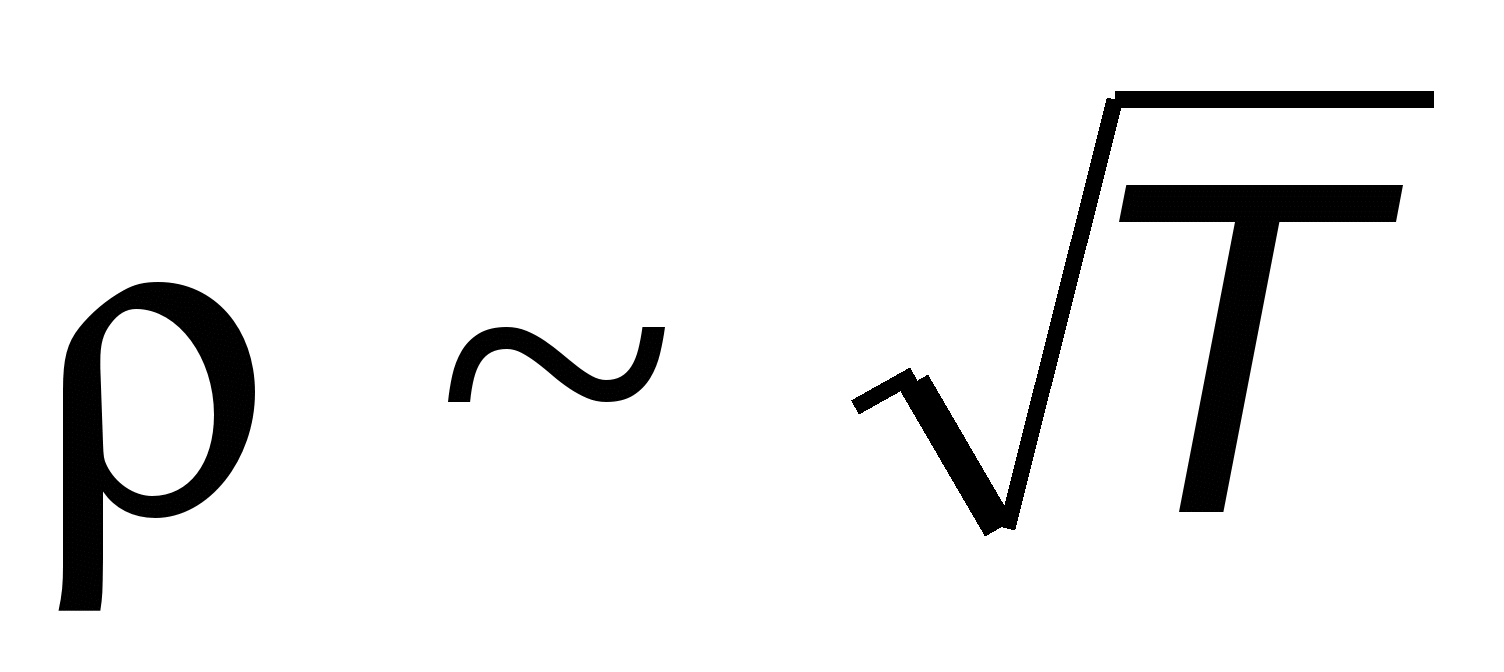 . Тим часом досвід показує, що лінійно залежить від температури
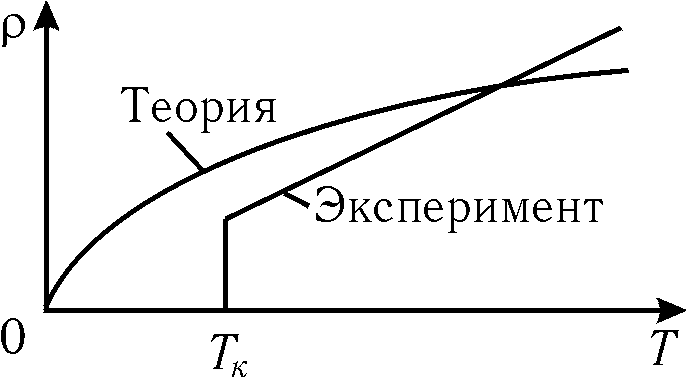
. Тим часом досвід показує, що лінійно залежить від температури 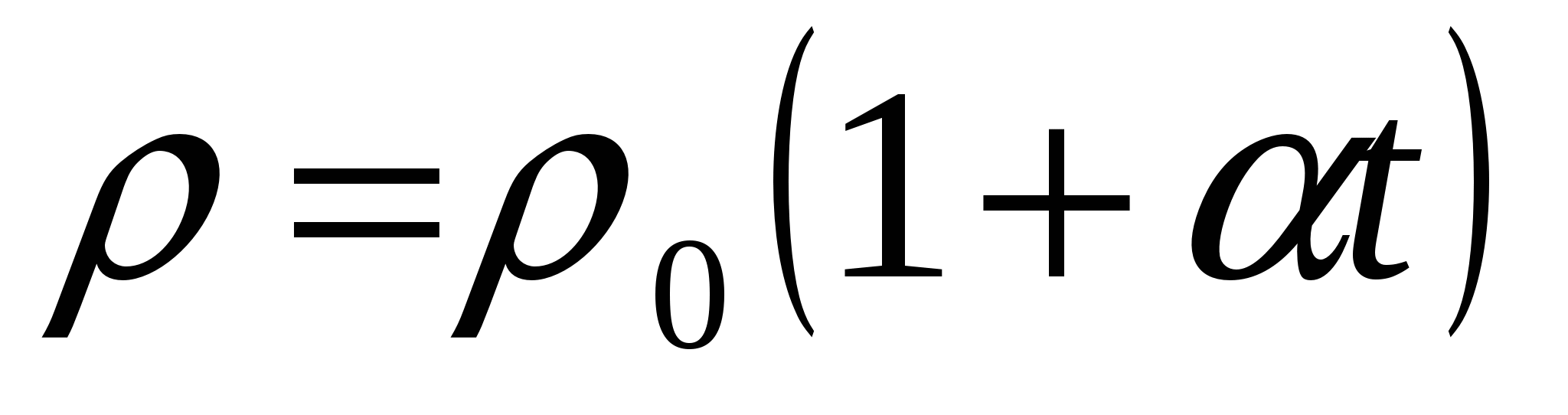 ,
,
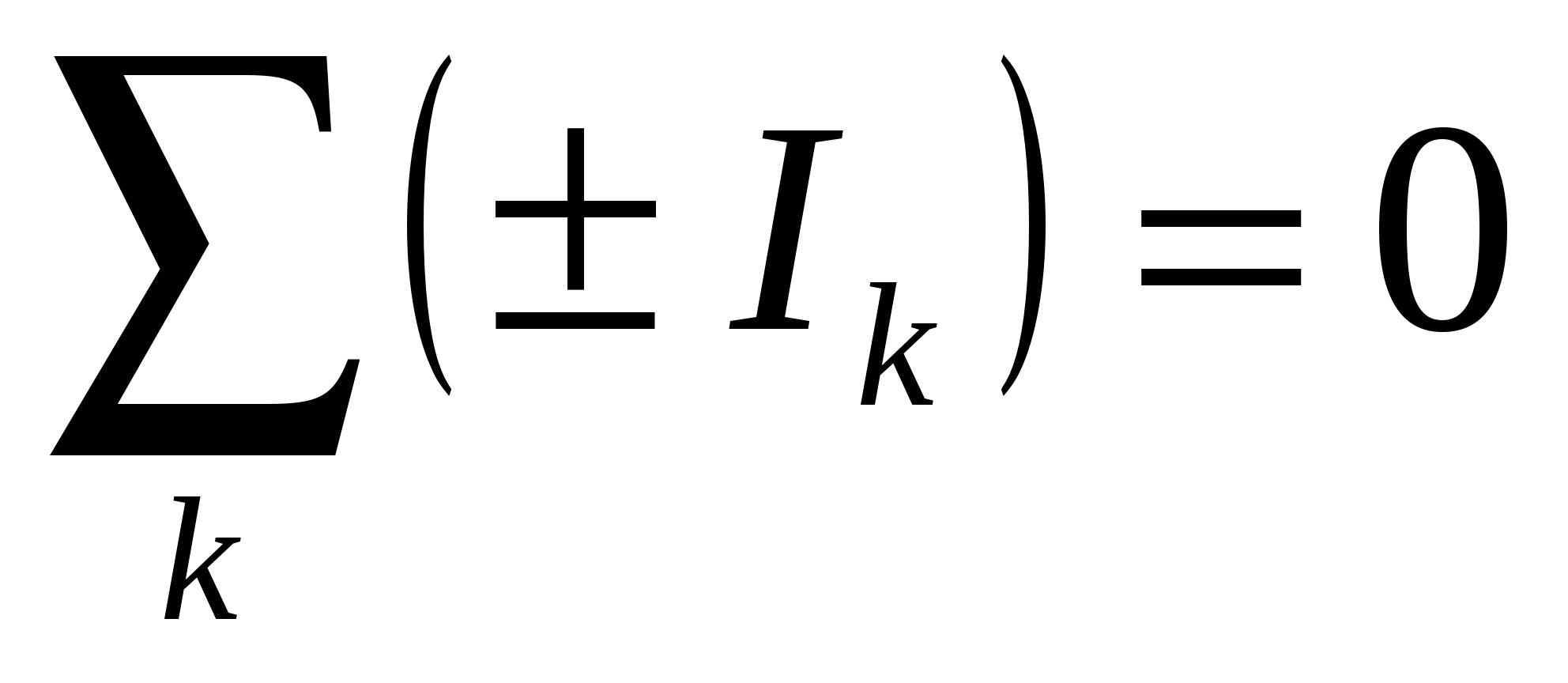 .
.
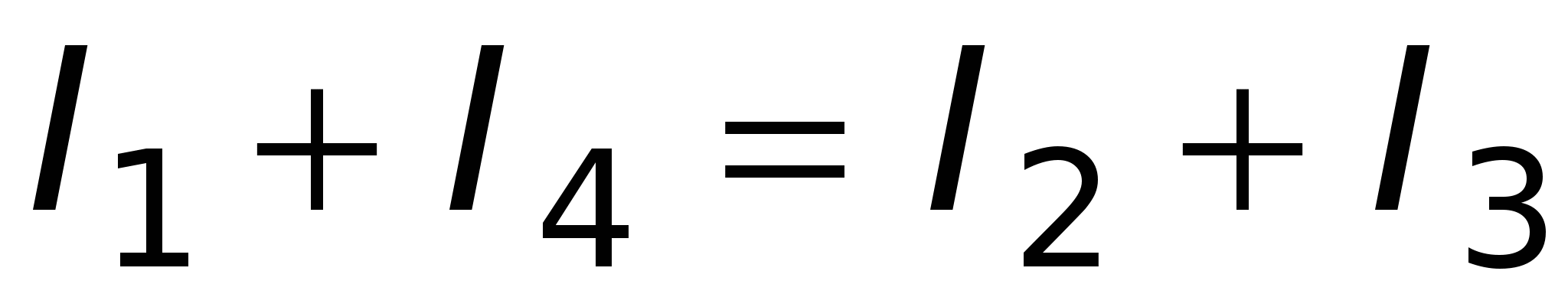 ,
,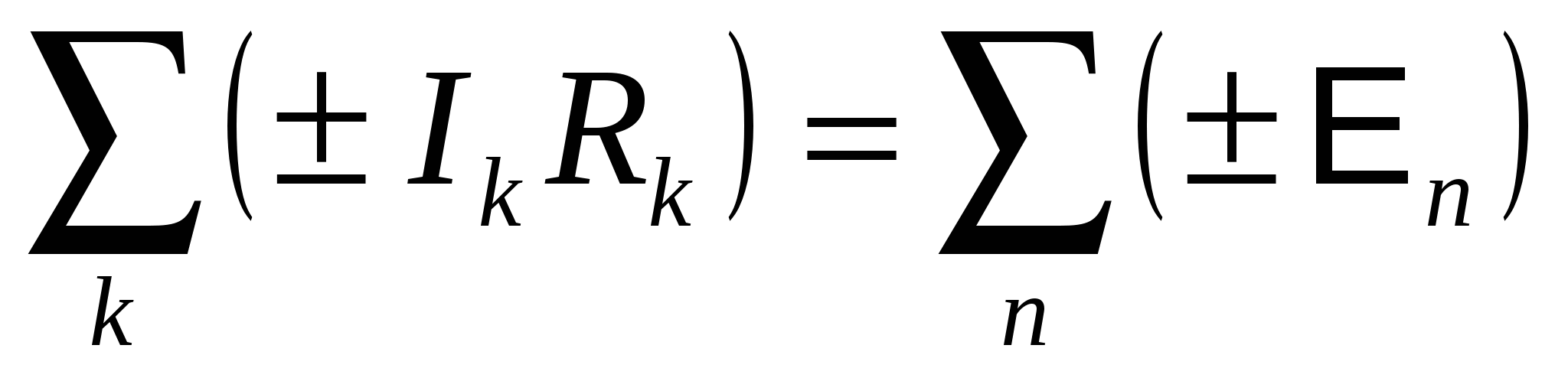 .
.